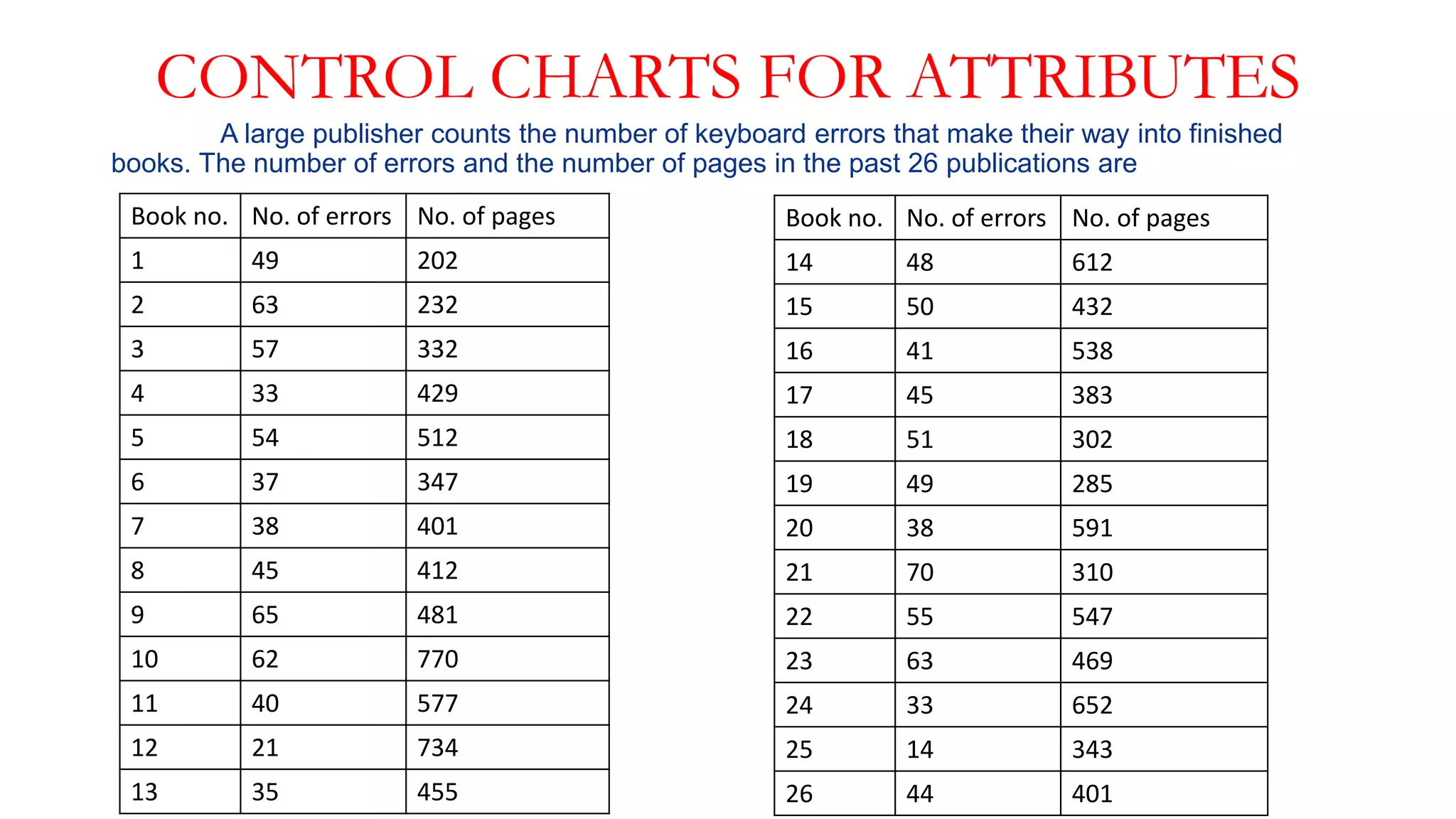
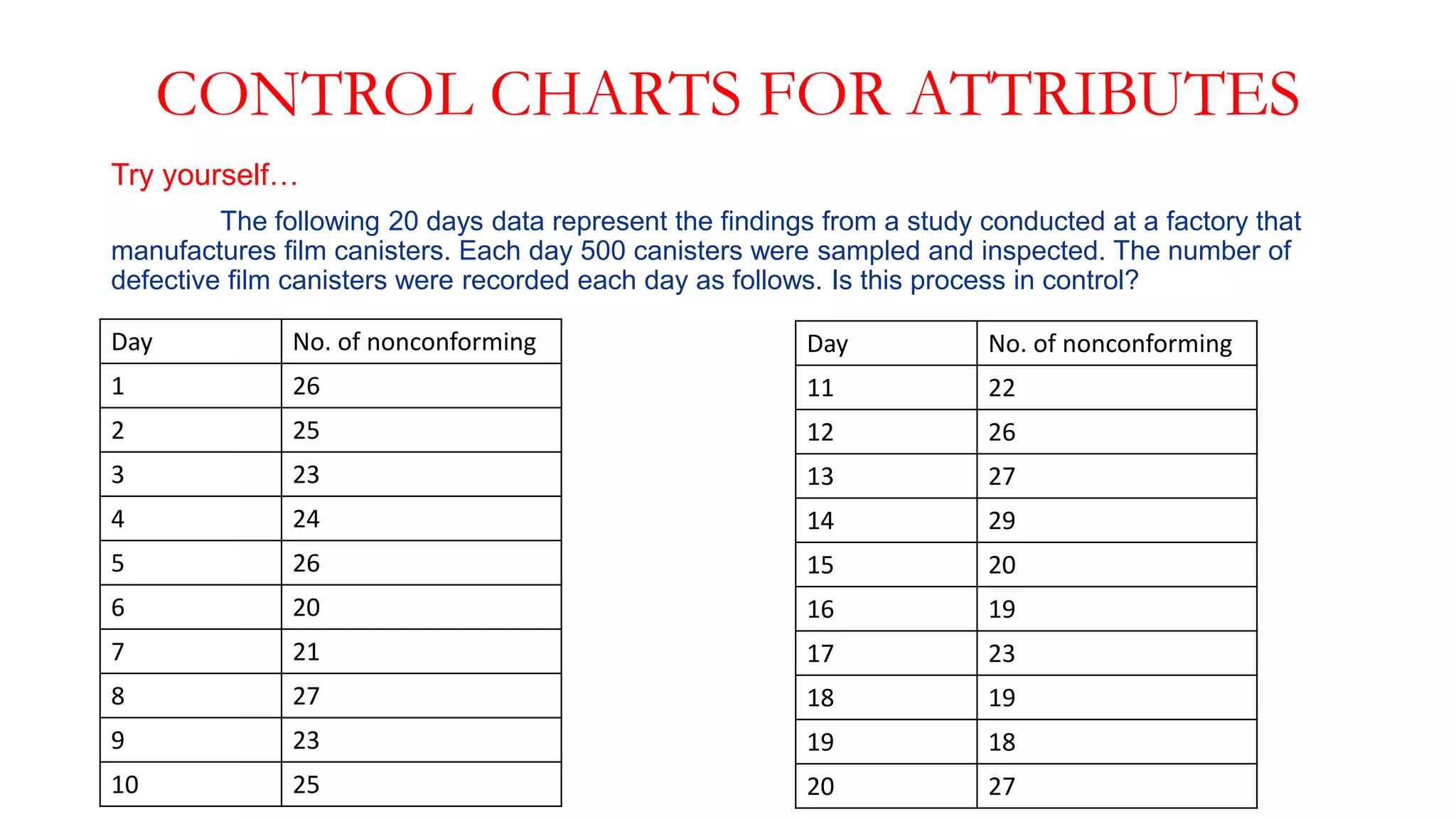
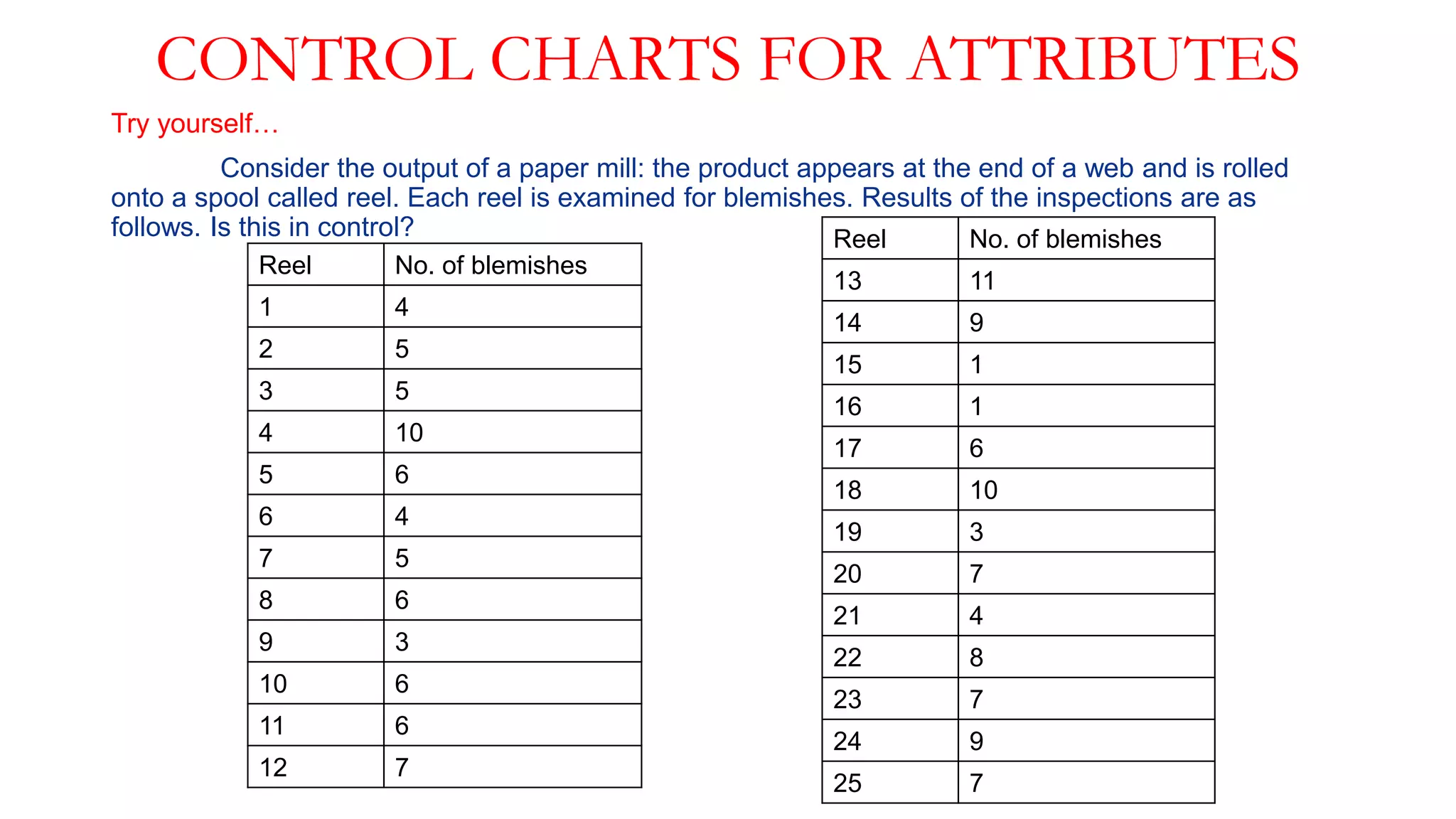
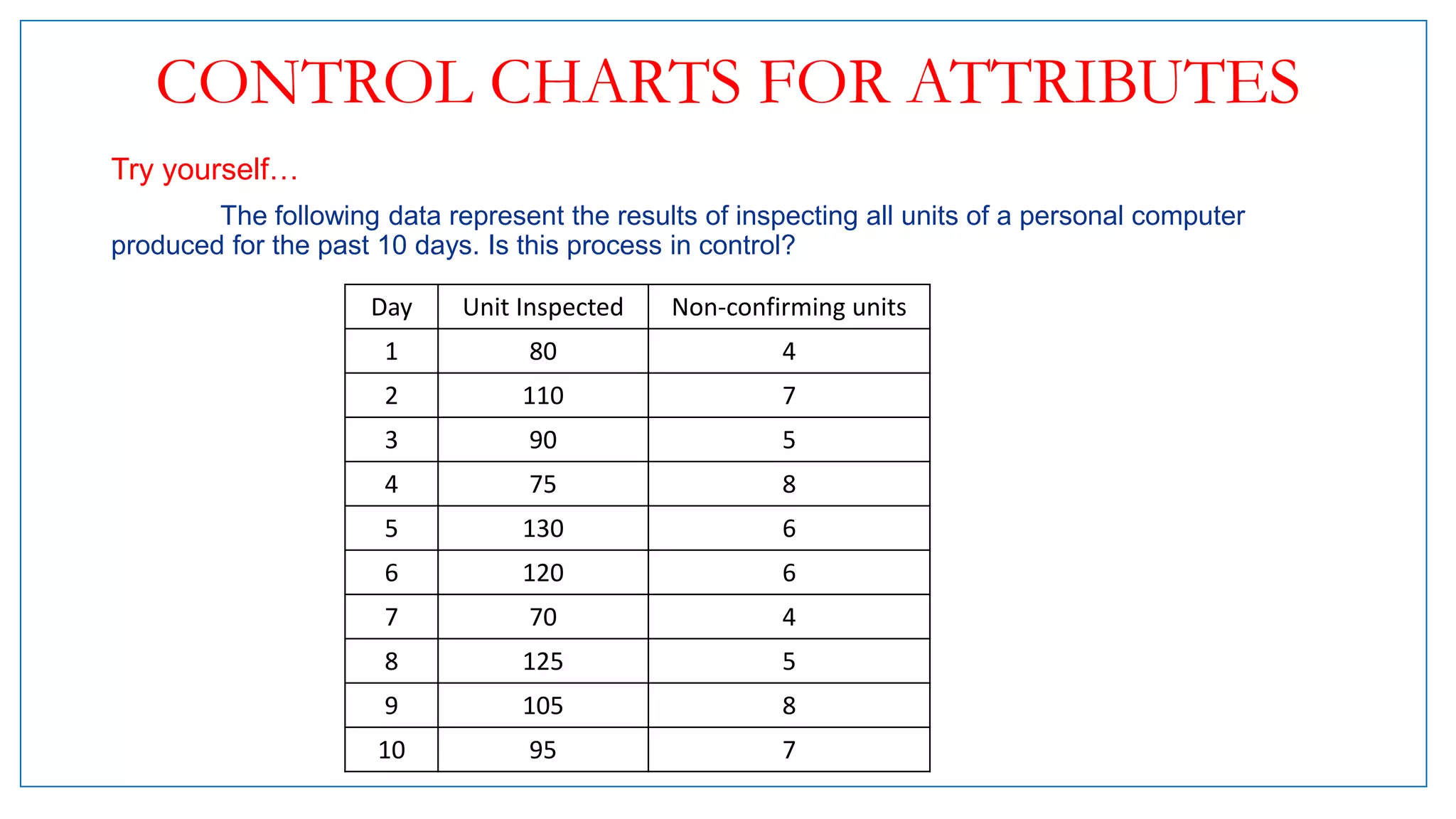
This document provides an overview of control charts, including:
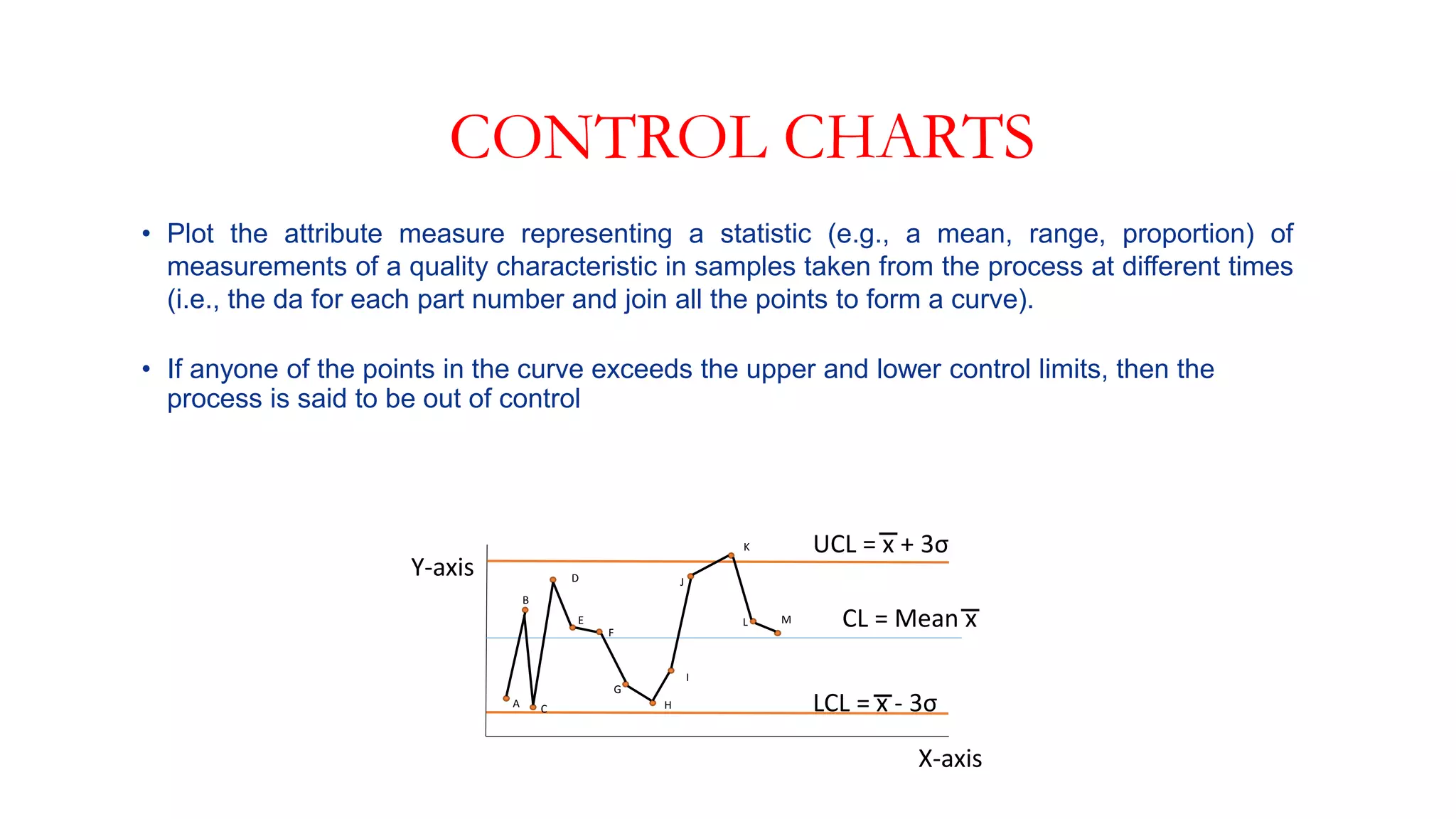
- Control charts are statistical tools used to monitor processes over time by analyzing variation. They have a central line for the average and upper and lower control limits.
- Walter Shewhart invented control charts in the 1920s to reduce failures and repairs in telephone transmission systems by distinguishing between common and special causes of variation.
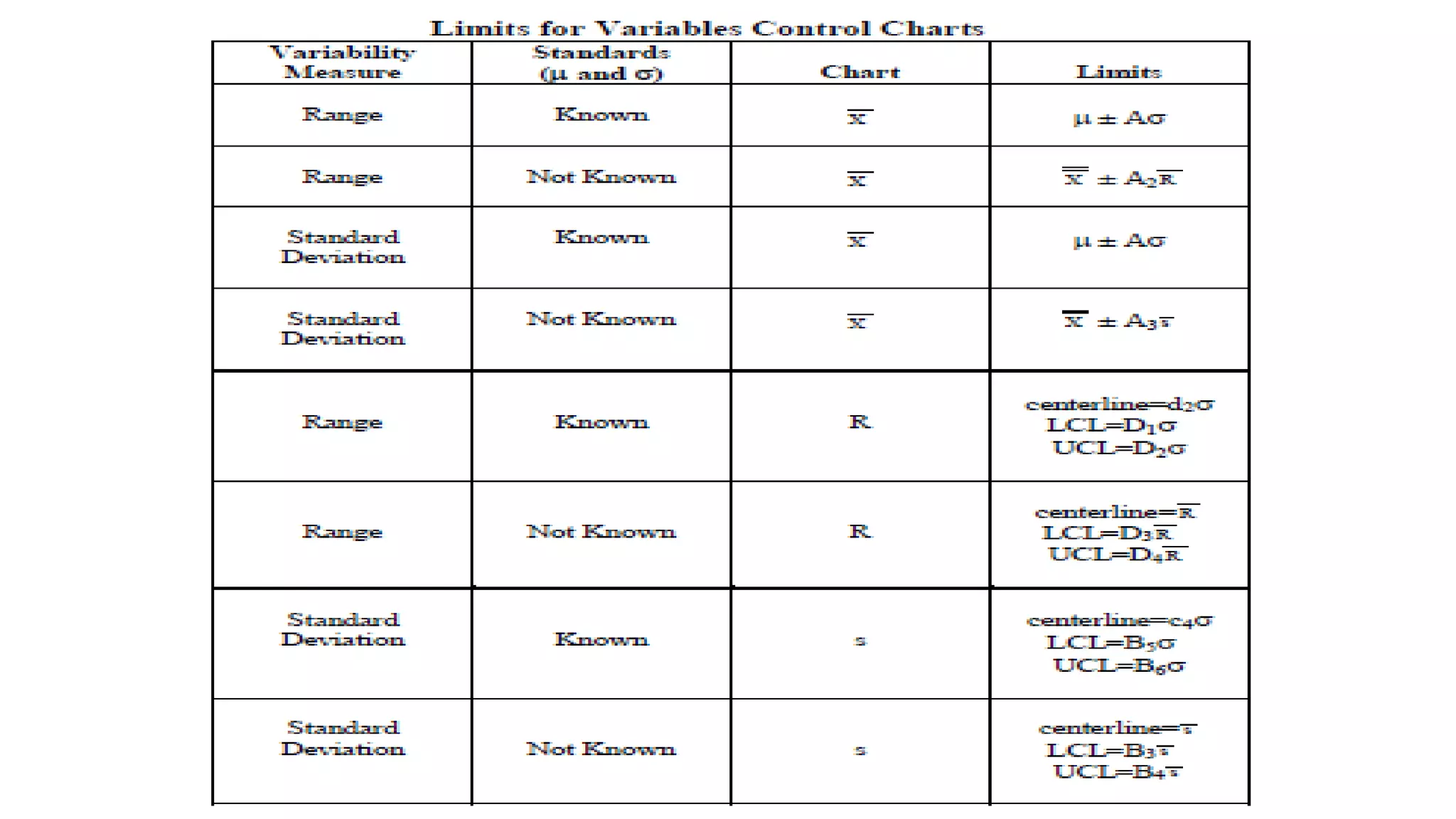
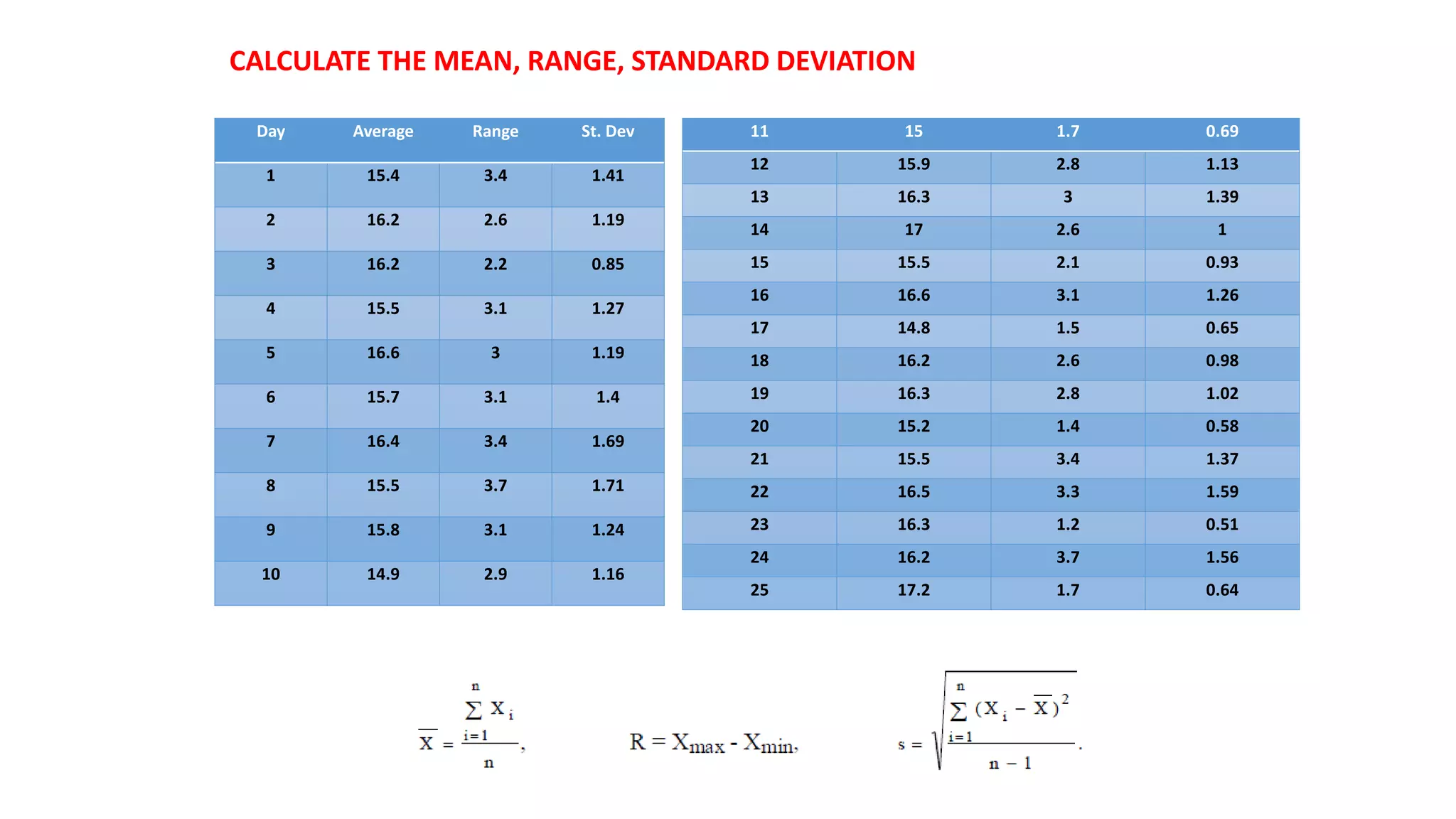
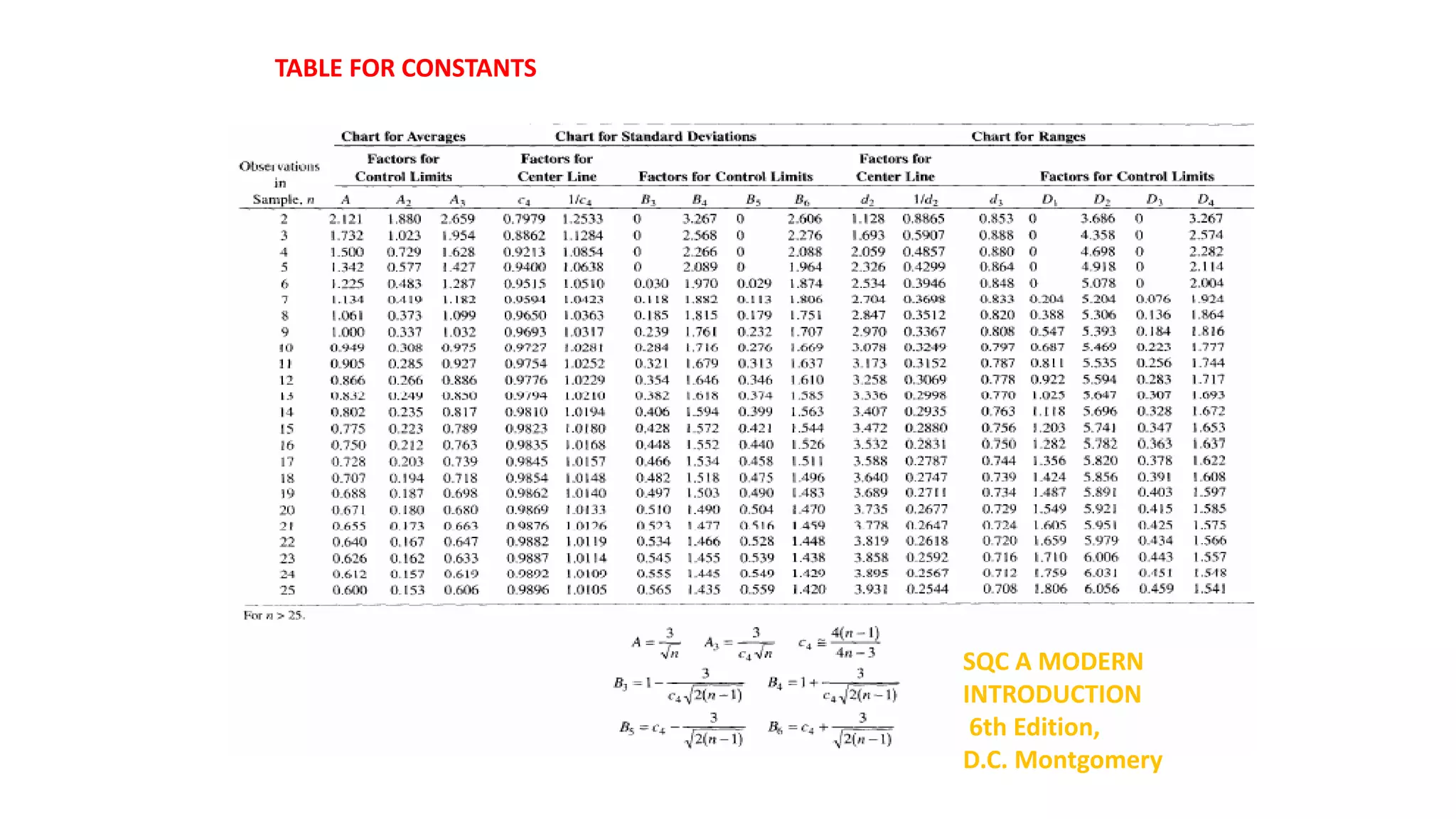
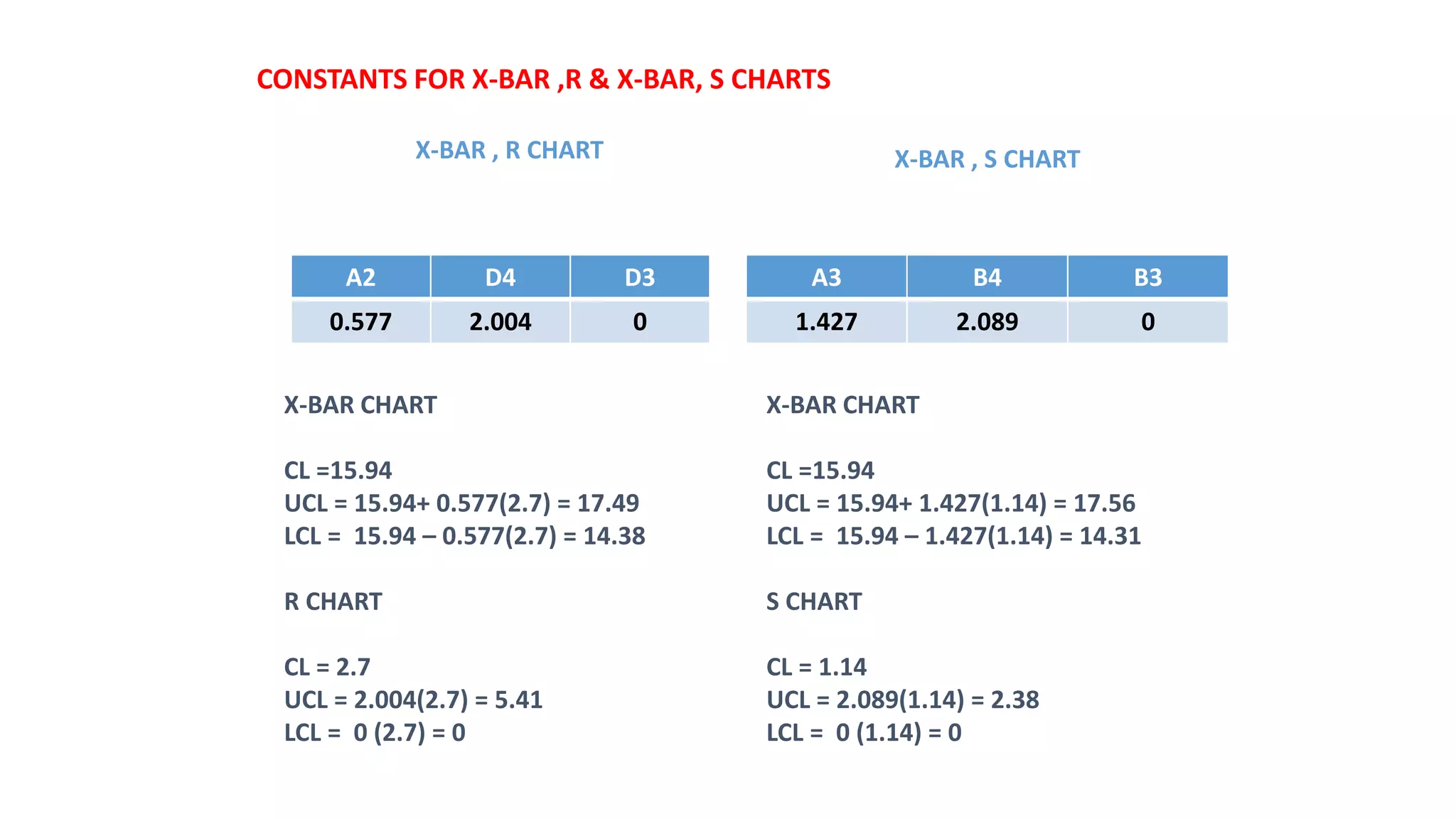
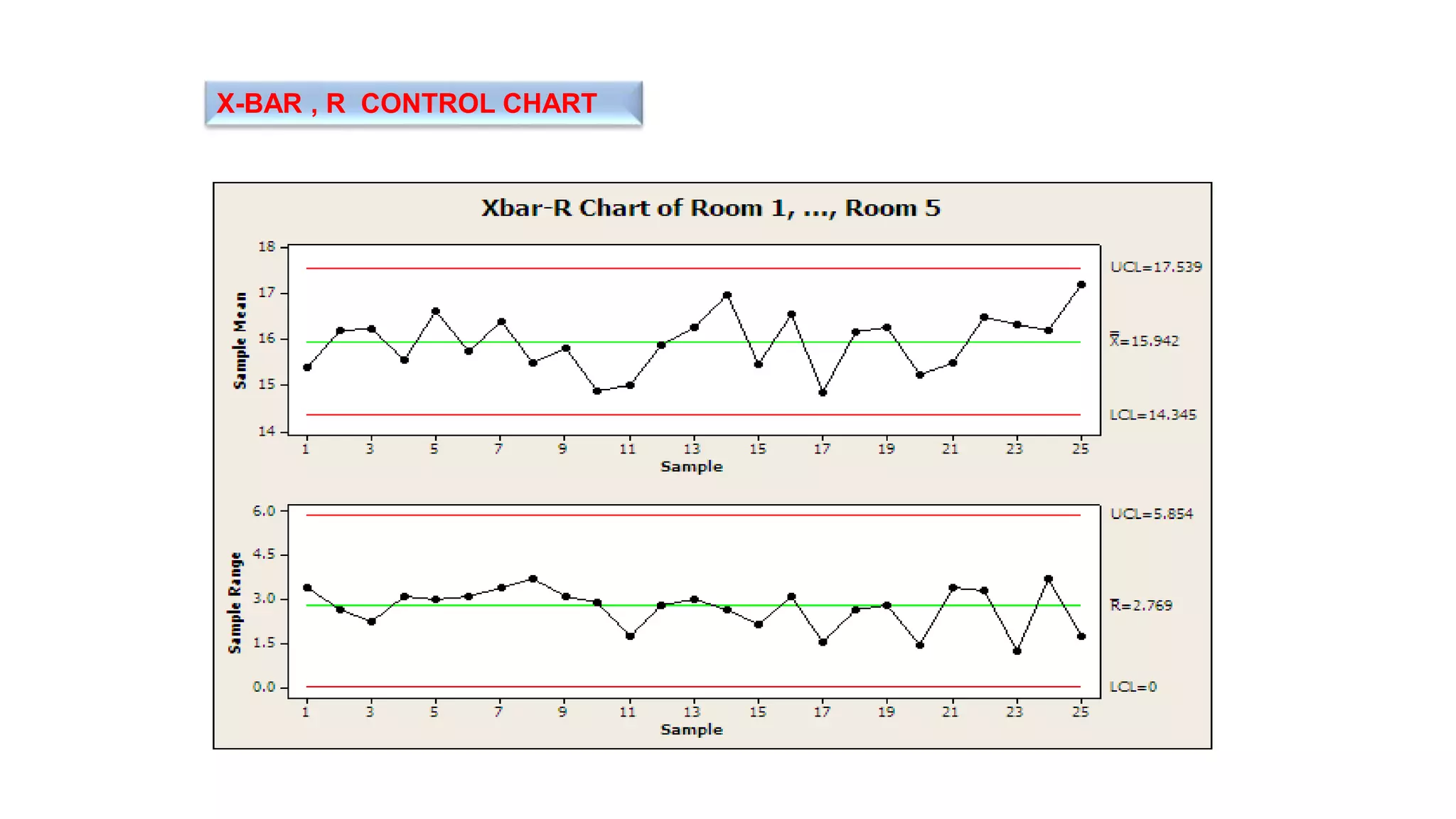
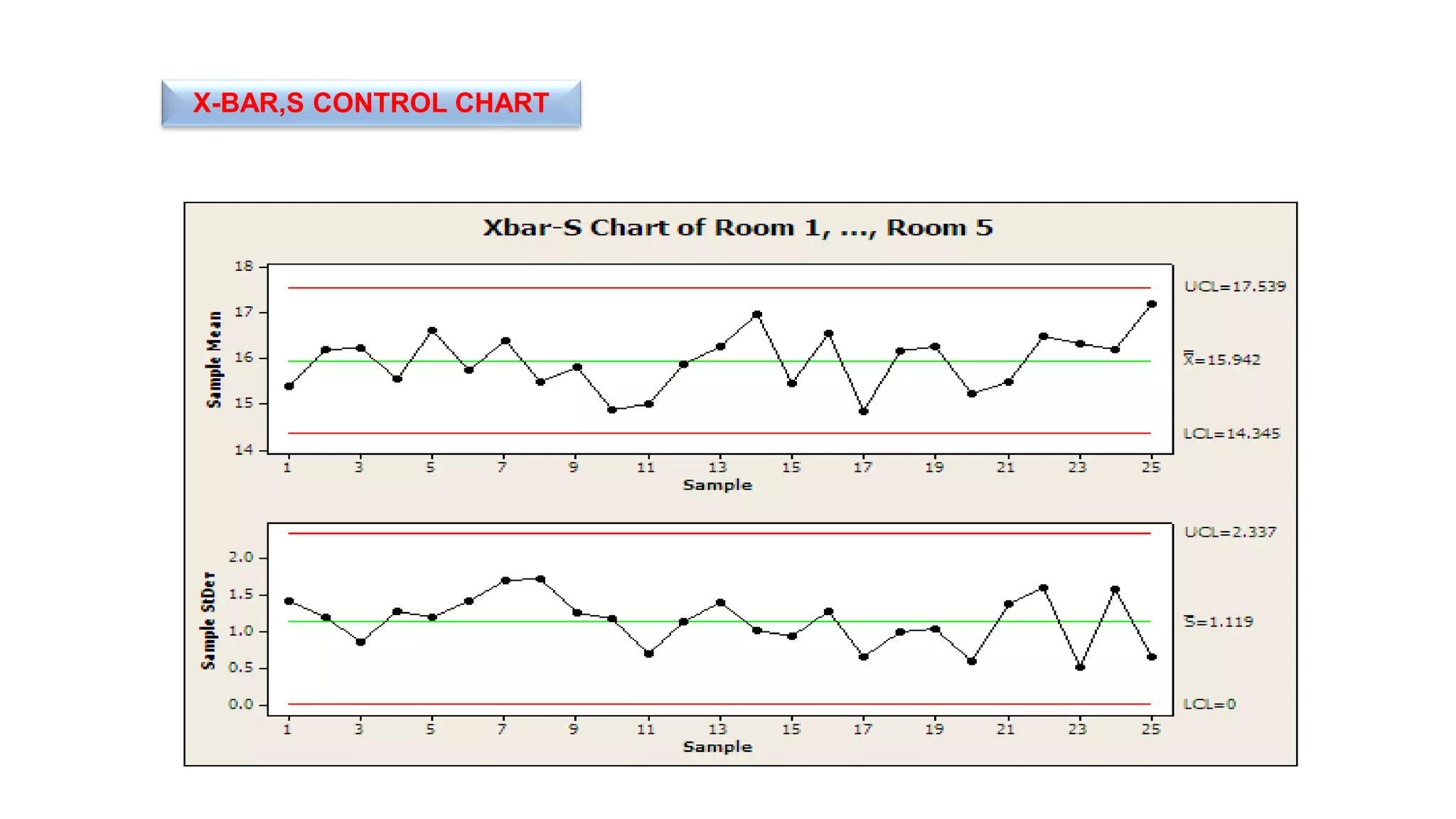
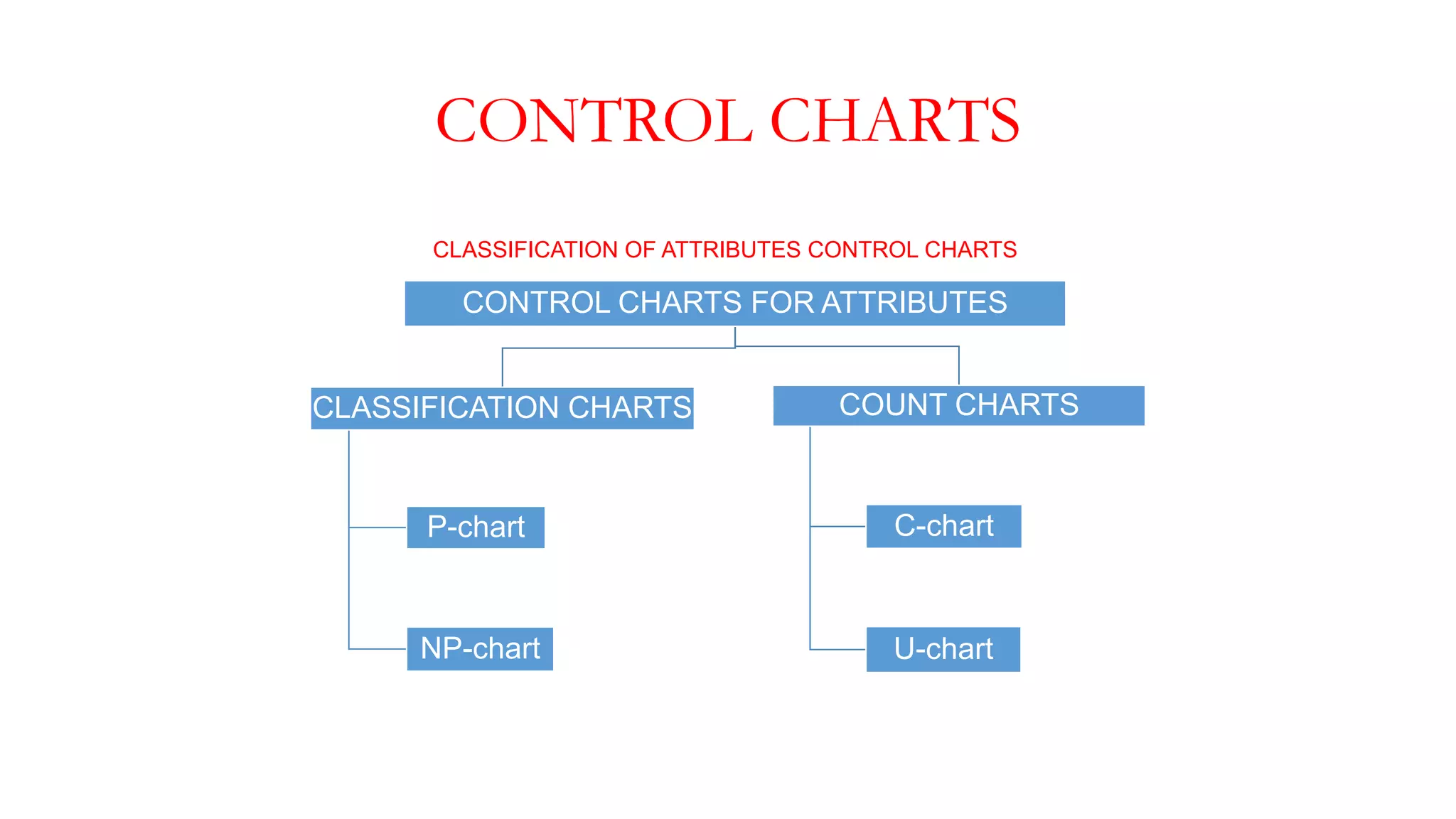
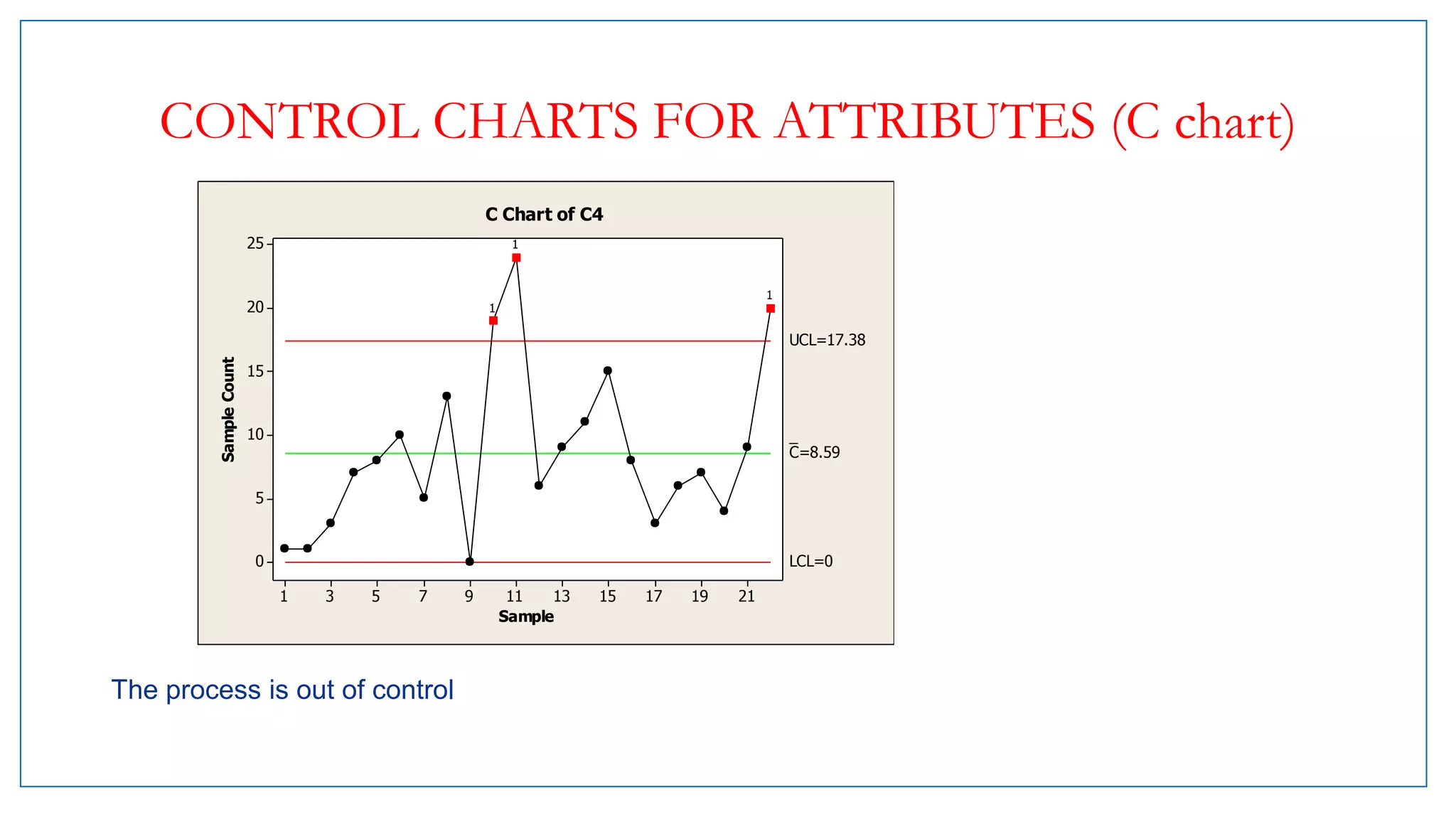
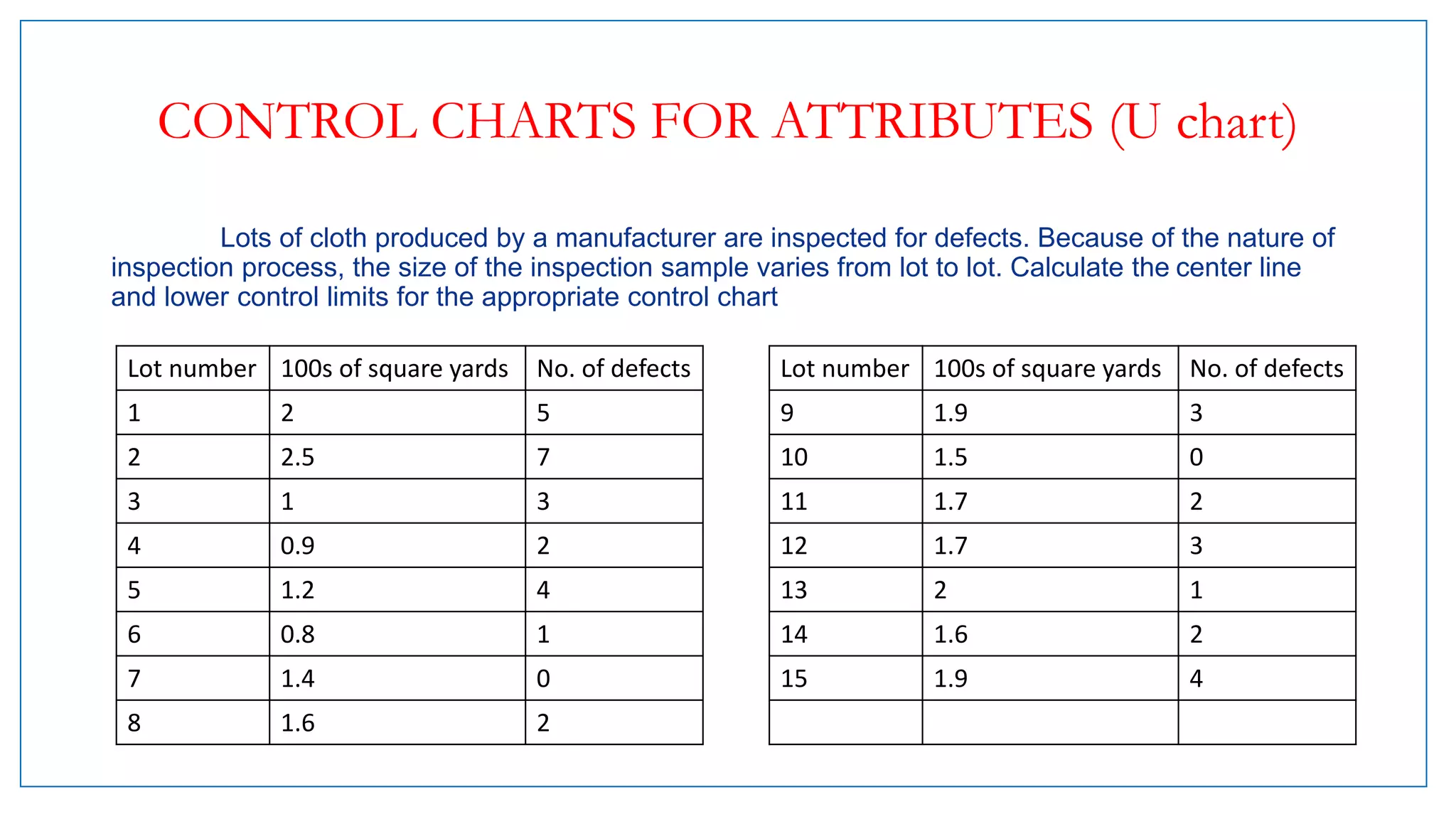
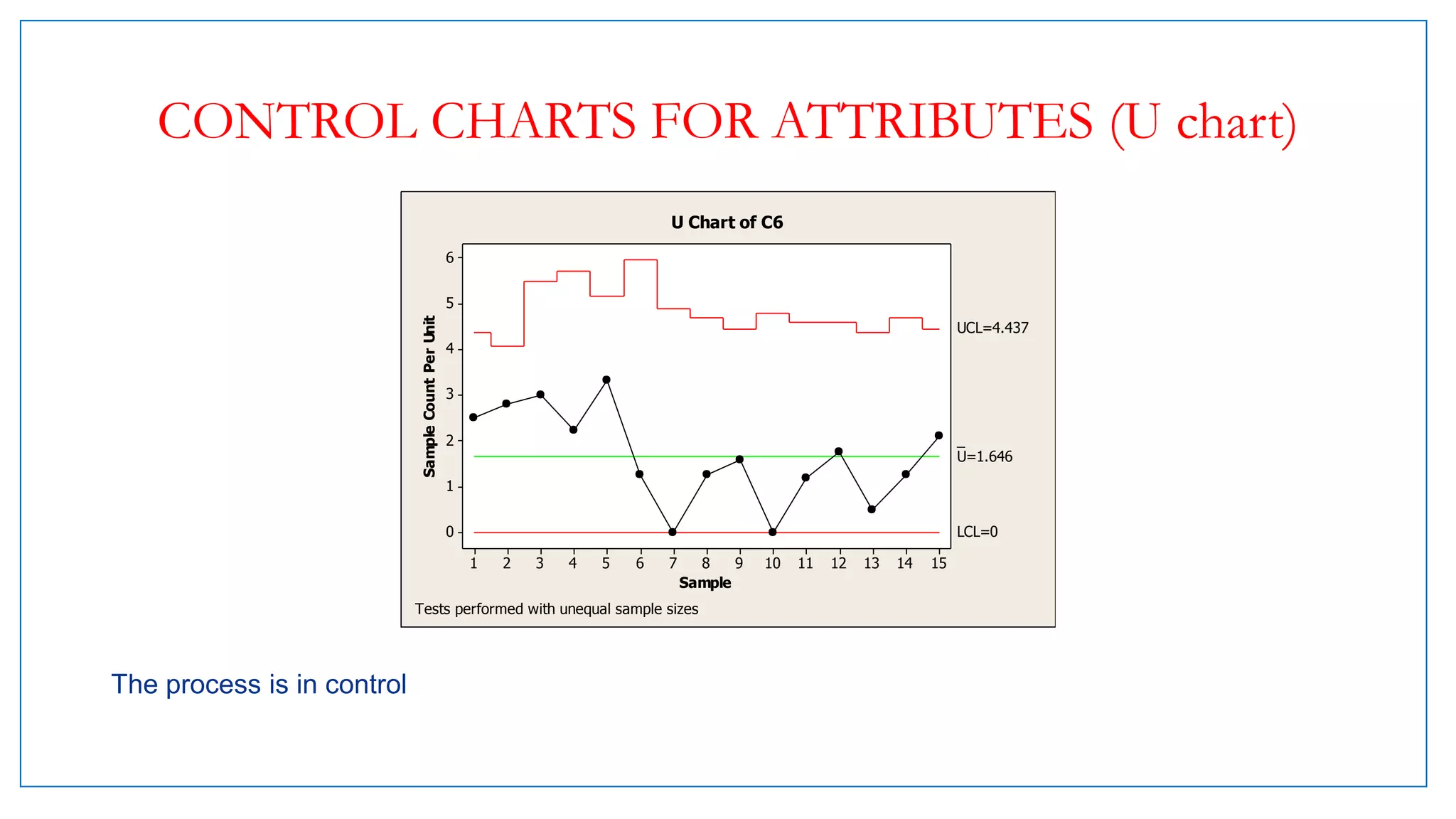
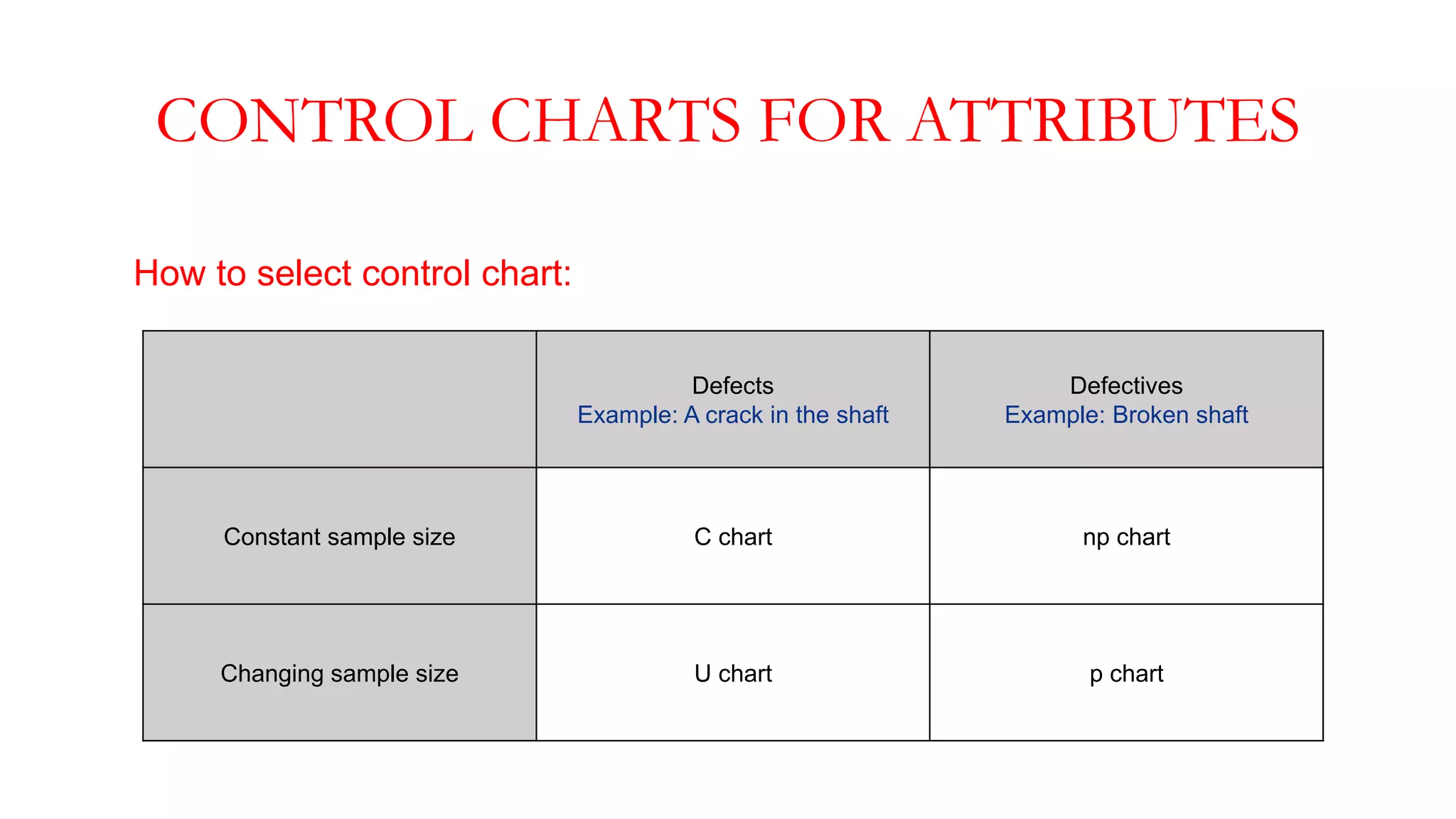
- There are variable control charts that monitor continuous data using statistics like the mean and range, and attribute control charts that monitor discrete data using statistics like defects per sample.
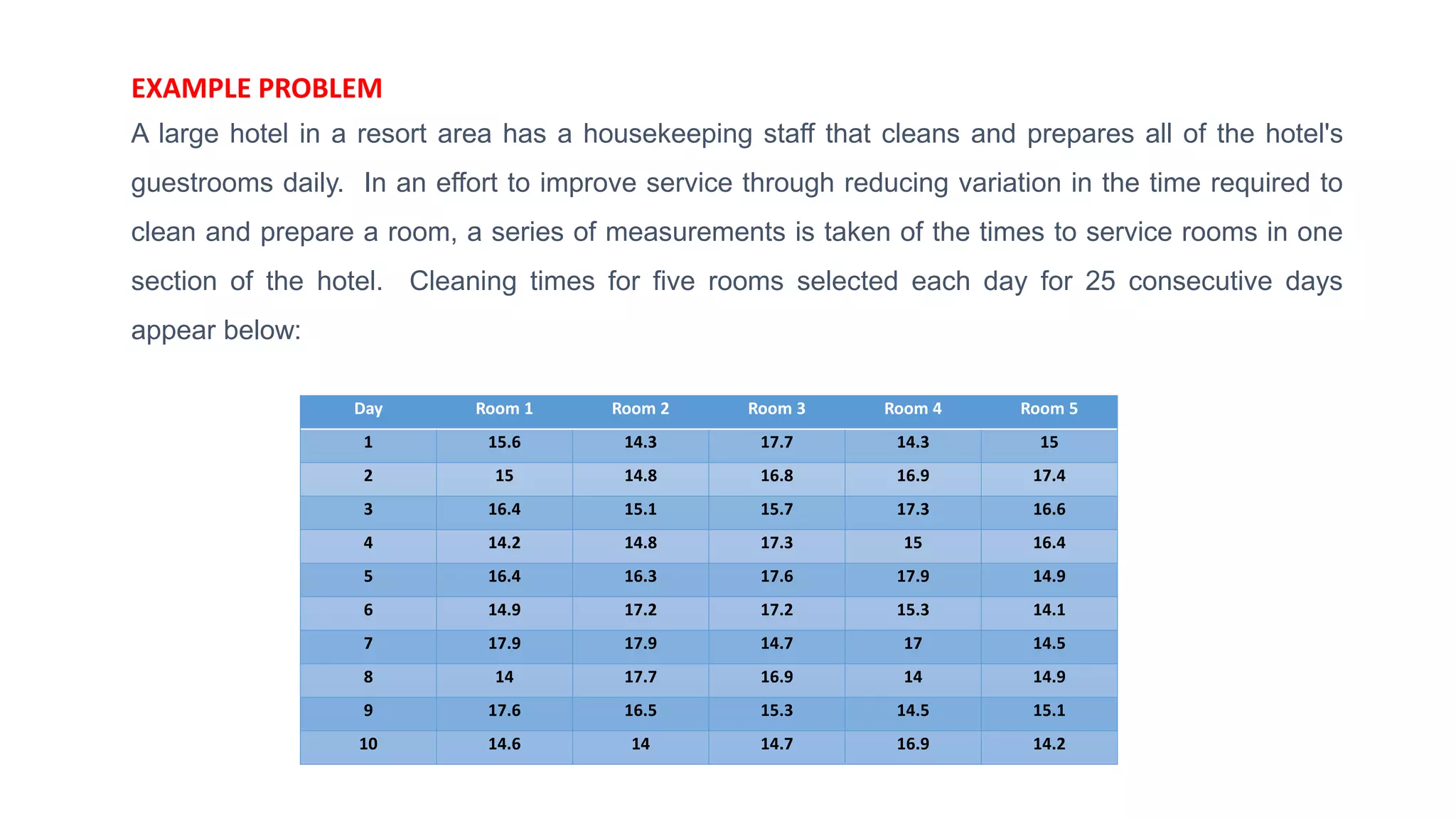
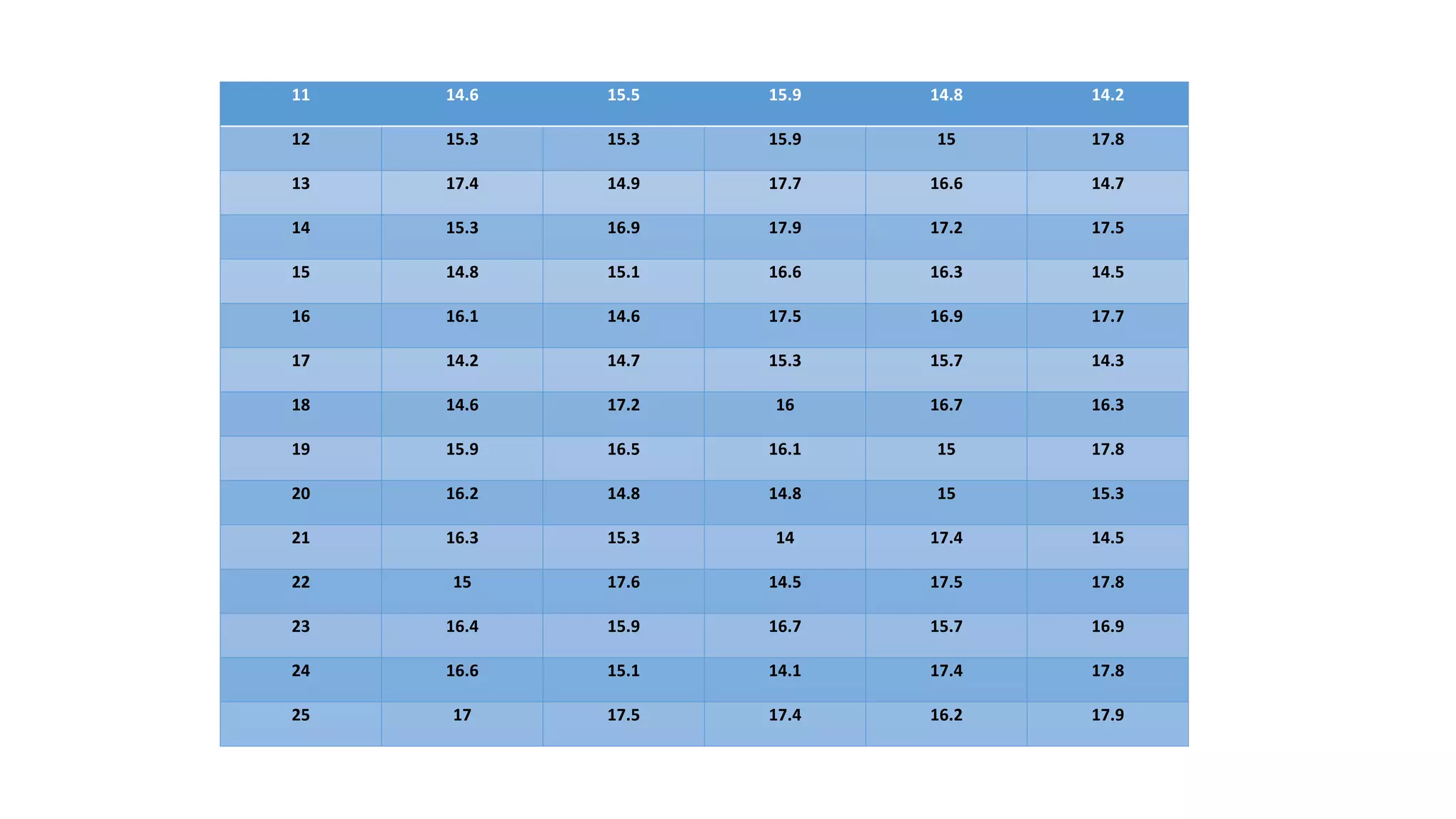
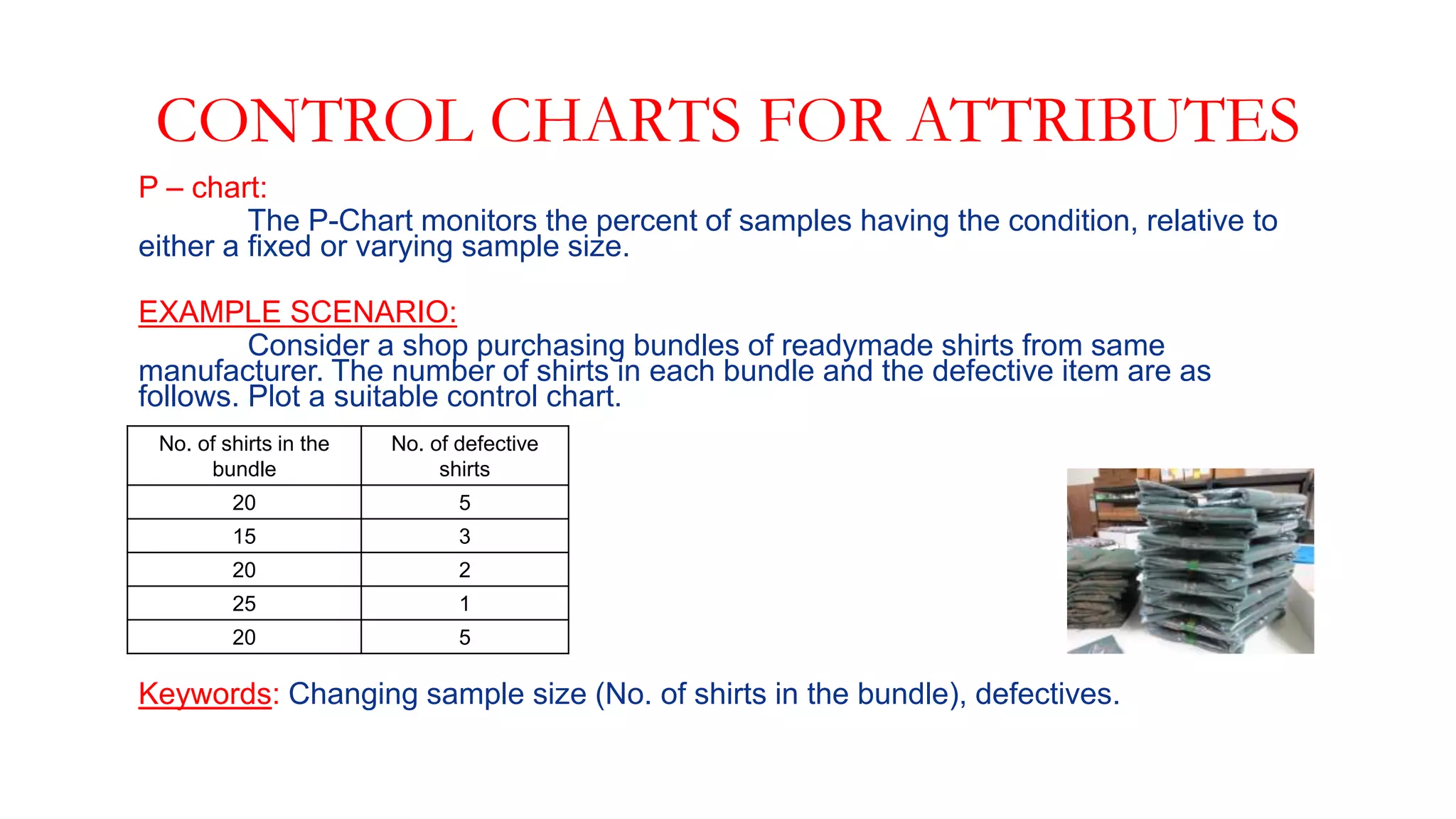
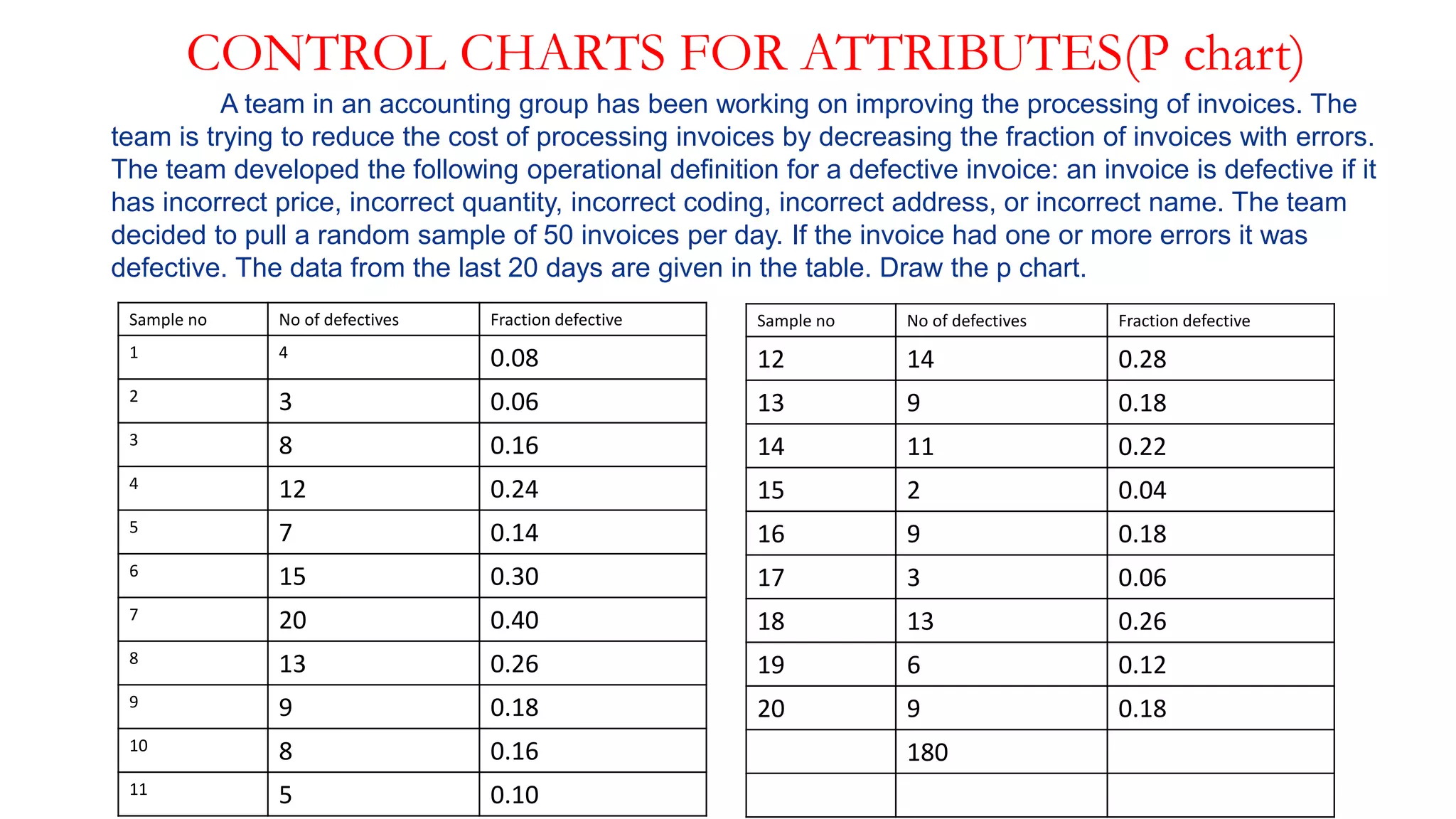
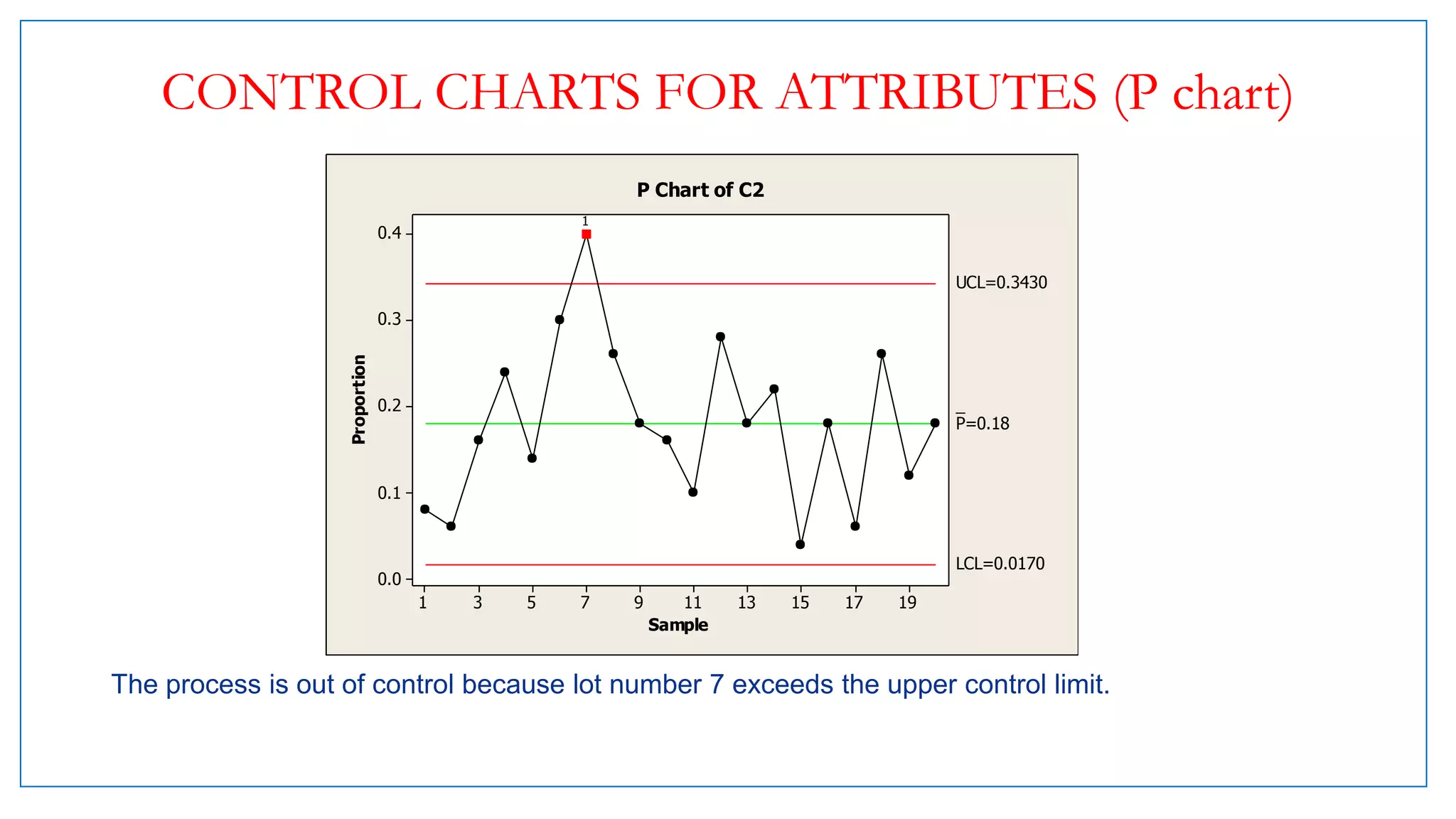
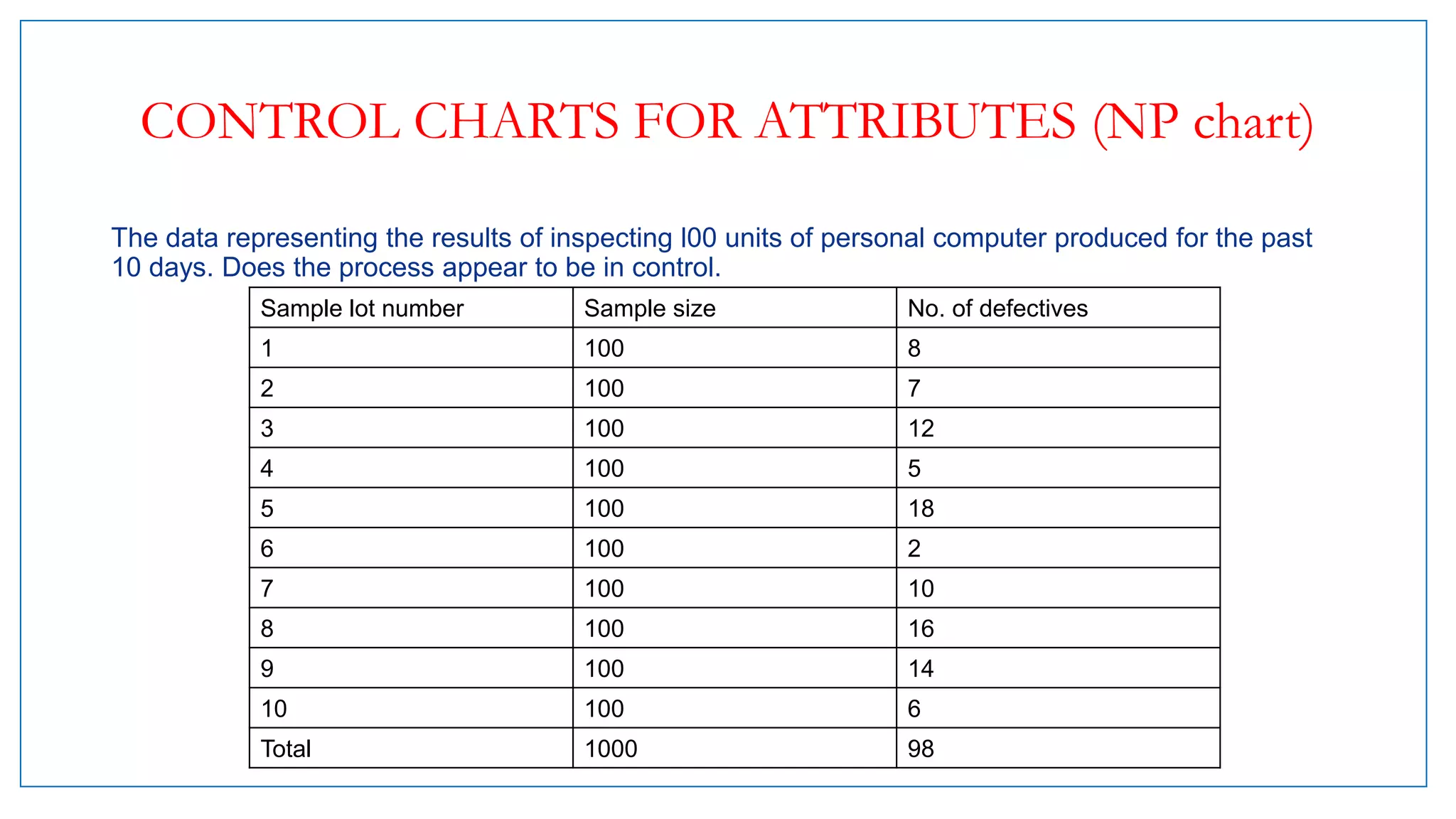
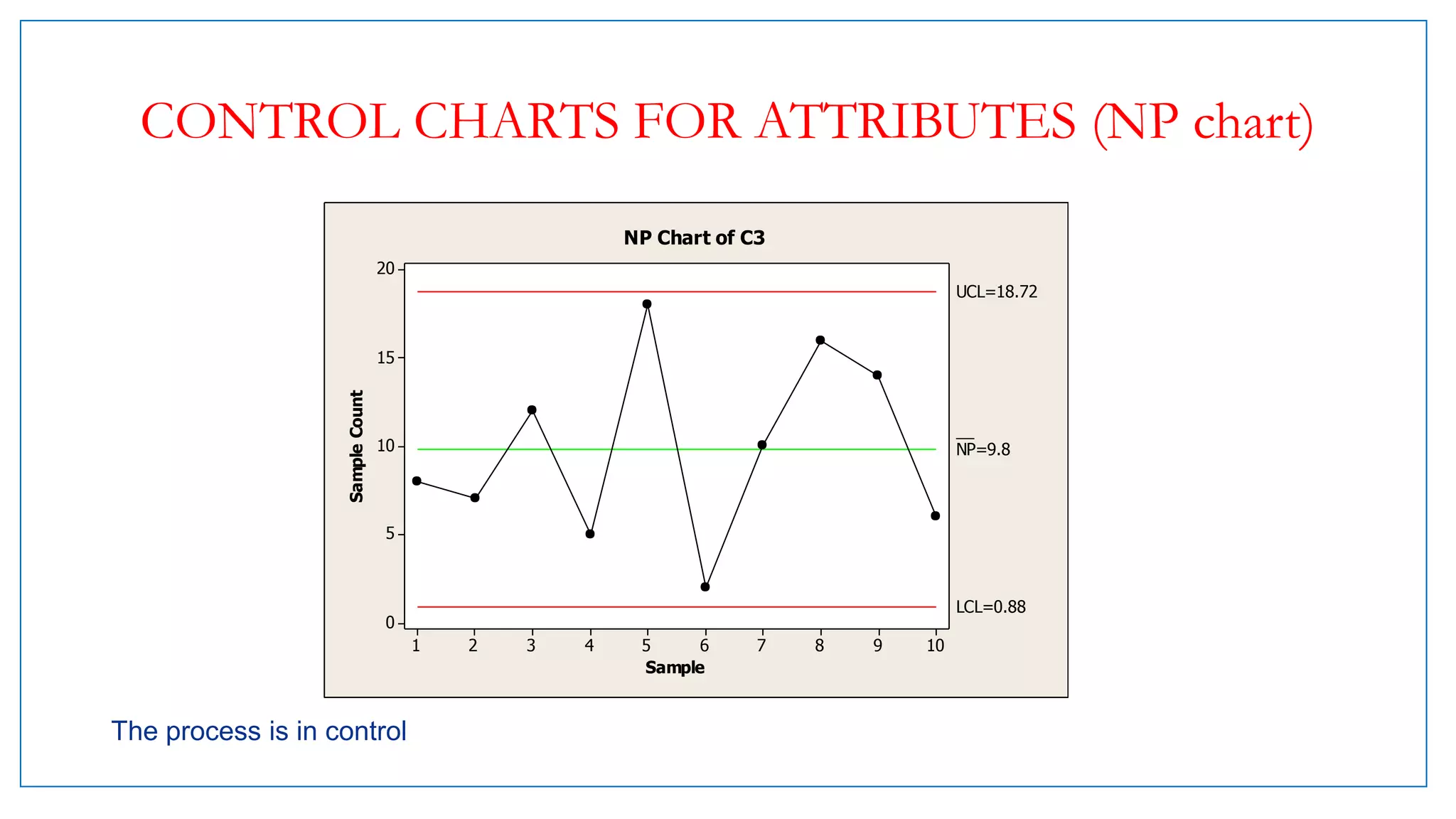
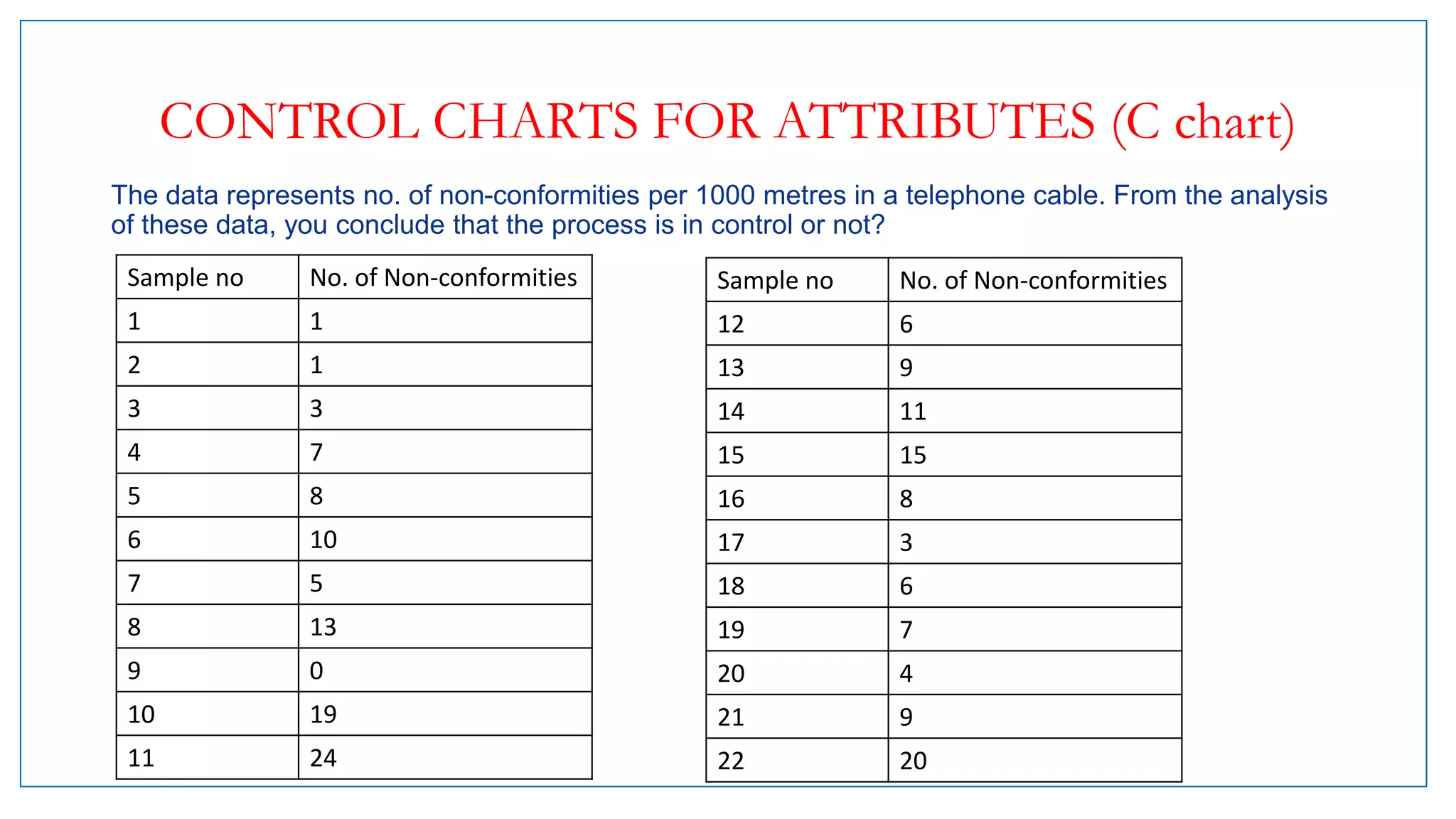
- Examples of control charts discussed include X-bar and R charts for variables, and P and NP charts for attributes. An example problem demonstrates how to construct and