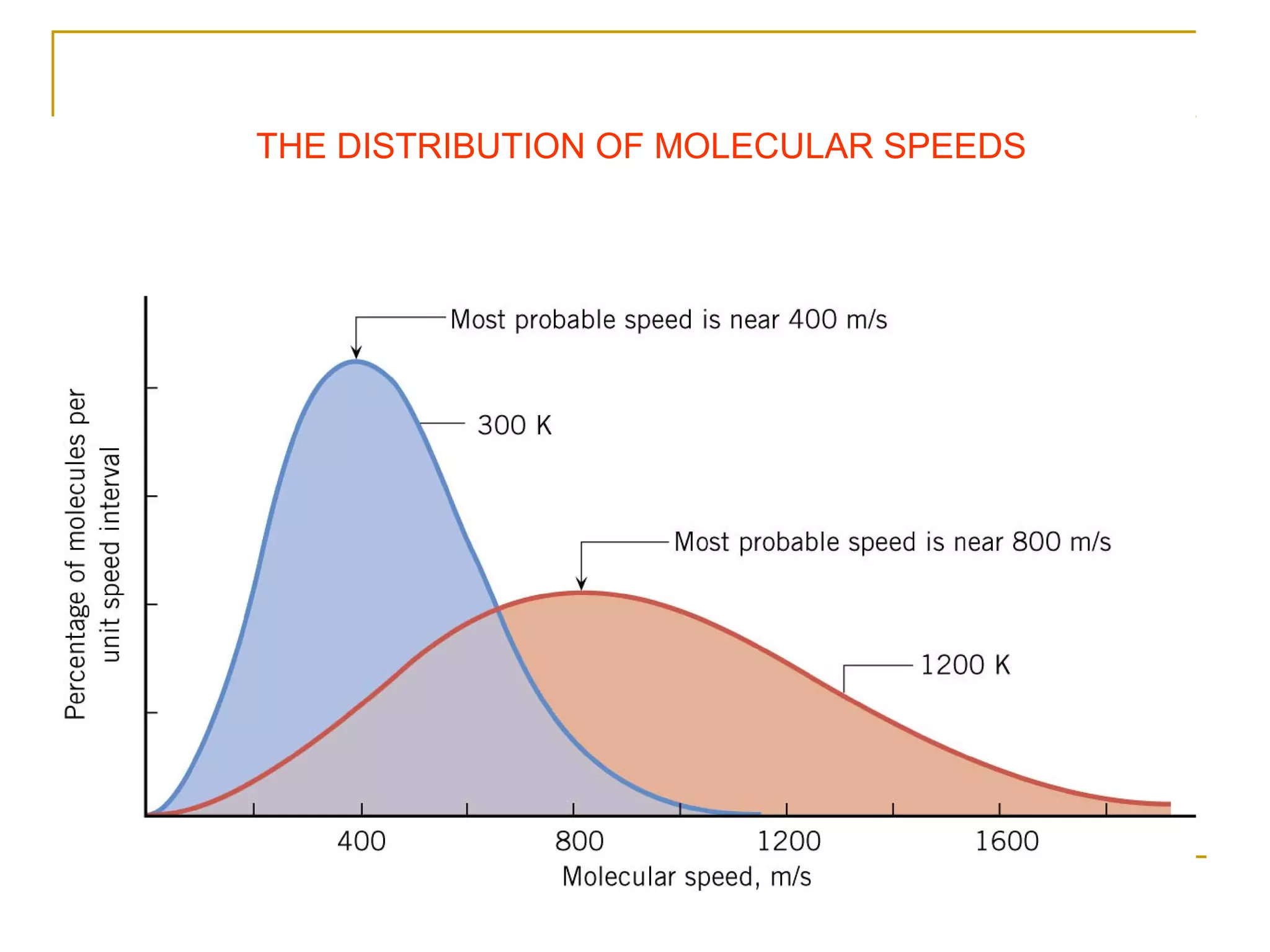
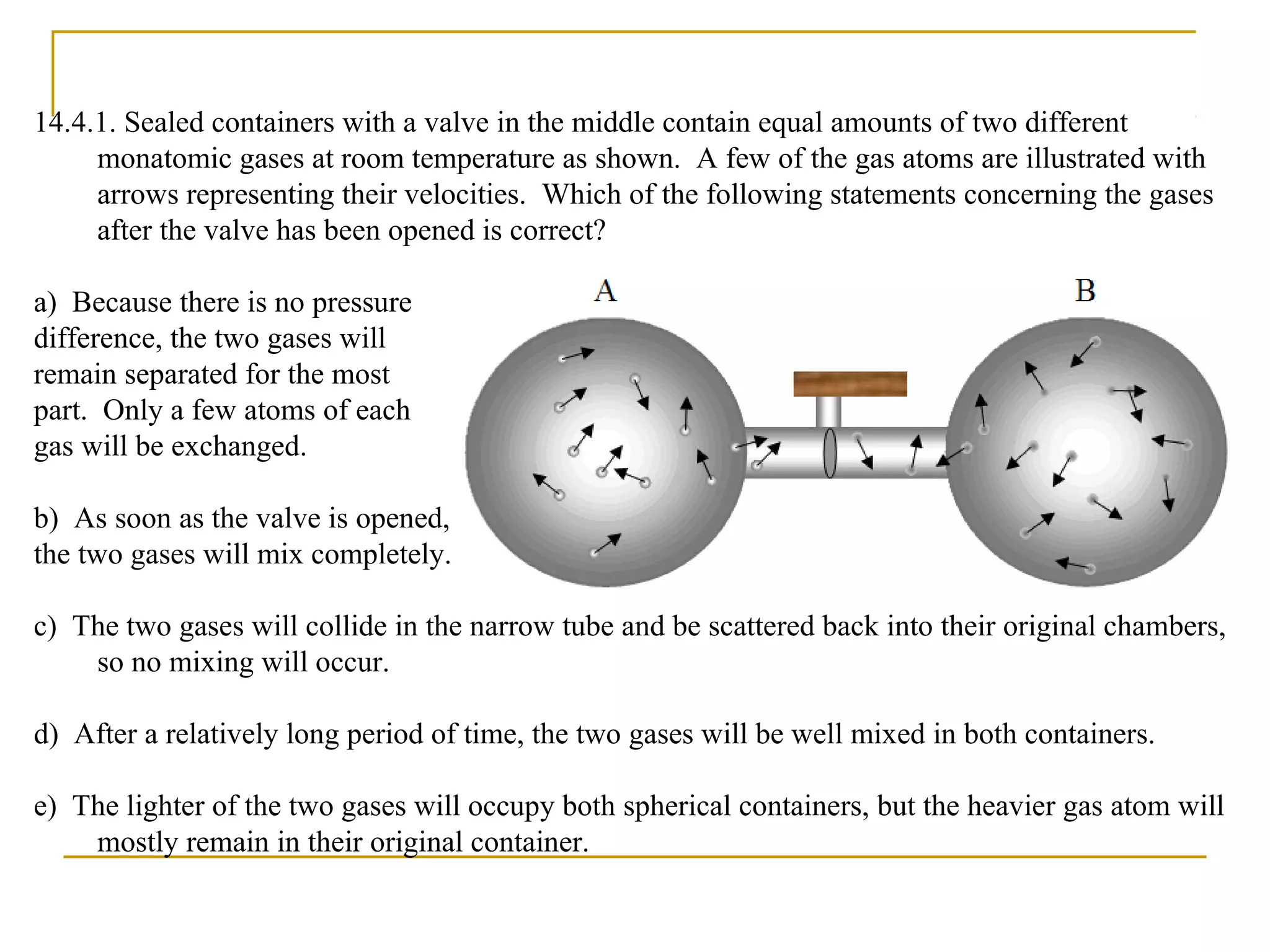
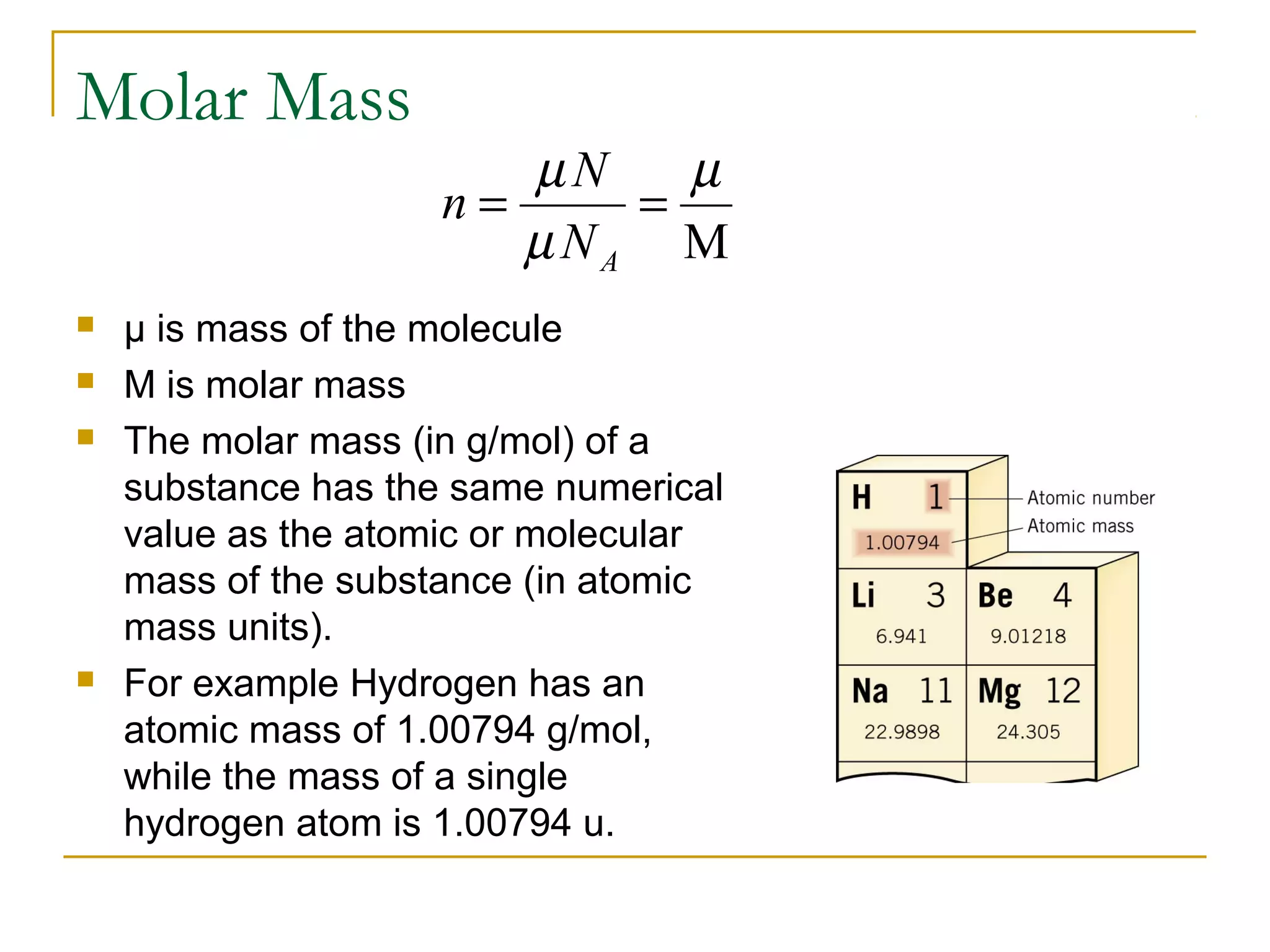
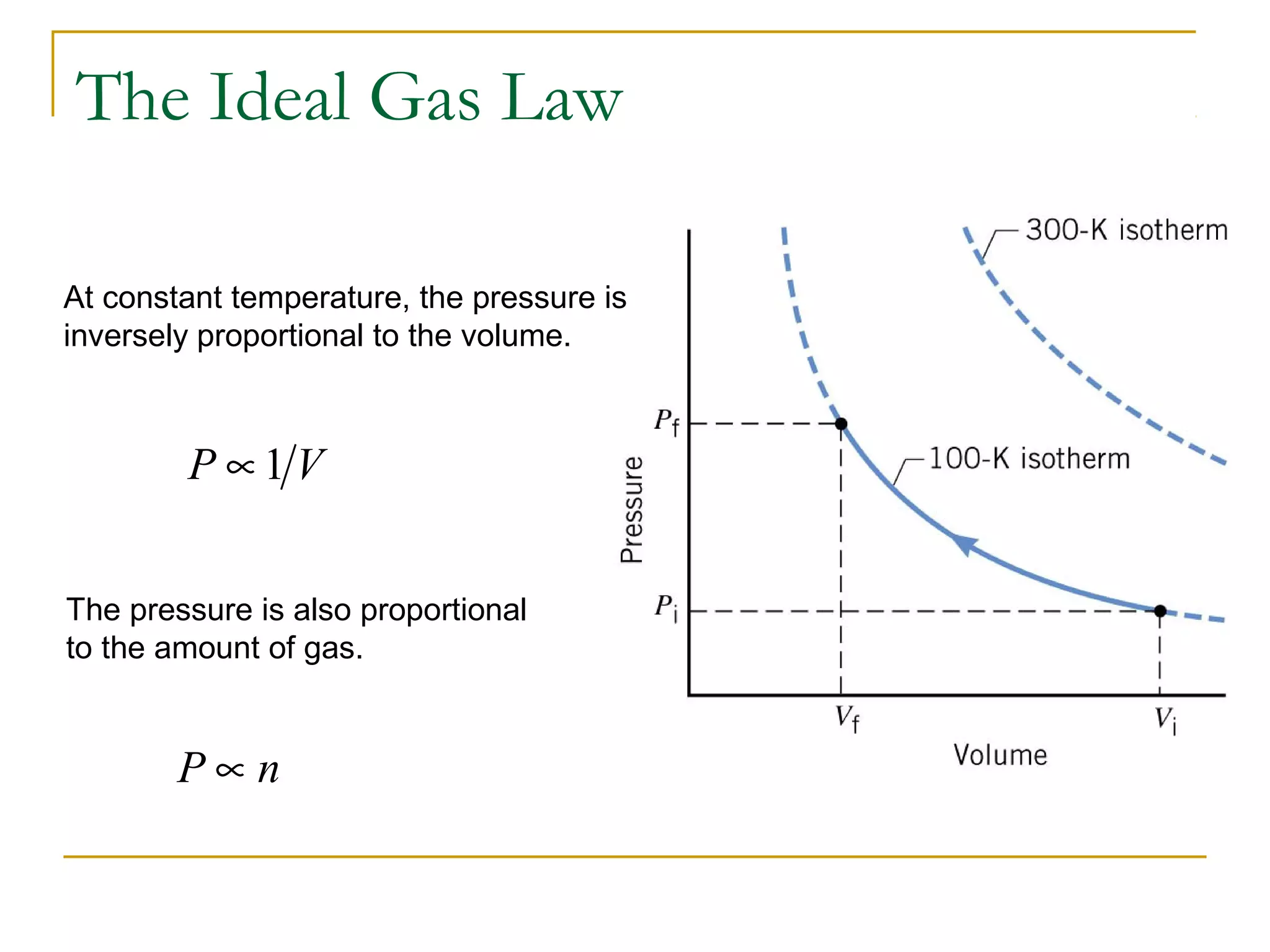
The document summarizes key concepts from Chapter 14 on the ideal gas law and kinetic theory. Section 1 discusses molecular mass, the mole, and Avogadro's number. Section 2 covers the ideal gas law and how pressure, volume, temperature, and moles are related. Section 3 introduces the kinetic theory model, which describes gases as large numbers of constantly moving particles and explains gas properties and behaviors in terms of particle collisions and kinetic energy.

1. Chapter 14
The Ideal Gas Law
& Kinetic Theory

2. AP Learning Objectives
Kinetic theory
 Ideal gases
 Students should understand the kinetic theory model of an ideal gas,
so they can:
 State the assumptions of the model.
 State the connection between temperature and mean
translational kinetic energy, and apply it to determine the
mean speed of gas molecules as a function of their mass and
the temperature of the gas.
 State the relationship among Avogadro’s number,
Boltzmann’s constant, and the gas constant R, and express
the energy of a mole of a monatomic ideal gas as a function
of its temperature.
 Explain qualitatively how the model explains the pressure of a
gas in terms of collisions with the container walls, and explain
how the model predicts that, for fixed volume, pressure must
be proportional to temperature.

3. Table of Contents
1. Molecular Mass, the Mole, Avogadro’s Number
2. Ideal Gas law
3. Kinetic Theory of Gases
4. Diffusion (AP?)

4. Chapter 14:
Ideal Gas Law & Kinetic Theory
Section 1:
Molecular Mass, the Mole, and Avogadro’s Number

5. Atomic Mass
 To facilitate comparison of the mass of one atom with
another, a mass scale know as the atomic mass scale
has been established.
 The unit is called the atomic mass unit (symbol u). The
reference element is chosen to be the most abundant
isotope of carbon, which is called carbon-12
 Carbon-12 is defined at 12 u
 The atomic mass is given in atomic mass units. For
example, a Li atom has a mass of 6.941u.
kg106605.1u1 27−
×=

6. 123
mol10022.6 −
×=AN
AN
N
n =
number of
moles
number of
atoms
The Mole & Avogadro’s Number
 One mole of a substance contains as many particles as
there are atoms in 12 grams of the isotope cabron-12.
 The number of atoms per mole is known as
 Avogadro’s number, NA.

7. M
µ
µ
µ
==
AN
N
n
Molar Mass
 μ is mass of the molecule
 M is molar mass
 The molar mass (in g/mol) of a
substance has the same numerical
value as the atomic or molecular
mass of the substance (in atomic
mass units).
 For example Hydrogen has an
atomic mass of 1.00794 g/mol,
while the mass of a single
hydrogen atom is 1.00794 u.

8. Example 1 The Hope Diamond and the Rosser Reeves Ruby
The Hope diamond (44.5 carats) is almost pure carbon. The Rosser
Reeves ruby (138 carats) is primarily aluminum oxide (Al2O3). One
carat is equivalent to a mass of 0.200 g. Determine (a) the number of
carbon atoms in the Hope diamond and (b) the number of Al2O3
molecules in the ruby.
M
µ
=n(a)
(b) ( ) ( ) ( )[ ]
molg96.101
carat1g200.0carats138
=
AnNN =
AnNN =
( ) ( ) ( )[ ]
molg011.12
carat1g200.0carats5.44
= mol741.0=
( )( )123
mol10022.6mol741.0 −
×= atoms1046.4 23
×=
M
µ
=n
( ) ( )

99.15398.262 +
mol271.0=
( )( )123
mol10022.6mol271.0 −
×= atoms1063.1 23
×=

9. 14.1.1. In 1865, Loschmidt calculated the number of molecules in a
cubic centimeter of a gas under standard temperature and pressure
conditions. He later used this number to estimate the size of an
individual gas molecule. Calculate Loschmidt’s number for helium
using the density, the atomic mass, and Avogadro’s number.
a) 2.7 × 1019
atoms/cm3
b) 3.5 × 1020
atoms/cm3
c) 4.1 × 1021
atoms/cm3
d) 5.4 × 1022
atoms/cm3
e) 6.2 × 1023
atoms/cm3

10. 14.1.2. Suppose that molecules of water (molecular mass = 0.01802 kg/m3
)
completely fill a container so that there is no empty space within the
container. Using the density of water and Avogadro’s number, estimate
the size of the water molecule. Hint: assume the water molecule fits
within a cube and that these cubes are stacked to fill the volume of the
container.
a) 4 × 10−11
m
b) 2 × 10−9
m
c) 3 × 10−10
m
d) 5 × 10−9
m
e) 6 × 10−10
m

11. 14.1.3. The standard for determining atomic masses is the carbon-12
atom, so that the mass of one mole of carbon-12 is exactly twelve
grams. What would Avogadro’s number and the atomic mass of
oxygen-16 be if the standard were that one mole of hydrogen is
exactly one gram?
a) 6.020 × 1023
mol−1
, 15.9898 grams
b) 6.069 × 1023
mol−1
, 16.1200 grams
c) 5.844 × 1023
mol−1
, 15.7845 grams
d) 5.975 × 1023
mol−1
, 15.8707 grams
e) 6.122 × 1023
mol−1
, 16.3749 grams

12. 14.1.4. Under which of the following circumstances does a real gas
behave like an ideal gas?
a) The gas particles move very slowly.
b) The gas particles do not collide with each other very often.
c) The interaction between the gas particles is negligible.
d) The interaction between the gas particles and the walls of the
container is negligible.
e) There are only one kind of particles in the container.

13. Chapter 14:
Ideal Gas Law & Kinetic Theory
Section 2:
The Ideal Gas Law

14. TP ∝
The Ideal Gas Law
 An ideal gas is an idealized
model for real gases that have
sufficiently low densities.
 The condition of low density
means that the molecules are so
far apart that they do not interact
except during collisions, which are
effectively elastic.
 At constant volume the pressure
is proportional to the temperature.

15. At constant temperature, the pressure is
inversely proportional to the volume.
VP 1∝
The pressure is also proportional
to the amount of gas.
nP ∝
The Ideal Gas Law

16. The absolute pressure of an ideal gas is directly proportional to the Kelvin
temperature and the number of moles of the gas and is inversely proportional
to the volume of the gas.
V
nRT
P =
nRTPV =
( )KmolJ31.8 ⋅=R
The Ideal Gas Law
V
nT
P ∝

17. TNkB=
AN
N
n =
( ) KJ1038.1
mol106.022
KmolJ31.8 23
123
−
−
×=
×
⋅
==
A
B
N
R
k
The Ideal Gas Law
nRTPV = T
N
R
N
A






=
Boltzmann’s Constant
TNknRTPV B==

18. Example 2 Oxygen in the Lungs
In the lungs, the respiratory membrane separates tiny sacs of air
(pressure 1.00x105
Pa) from the blood in the capillaries. These sacs
are called alveoli. The average radius of the alveoli is 0.125 mm, and
the air inside contains 14% oxygen. Assuming that the air behaves as
an ideal gas at 310K, find the number of oxygen molecules in one of
these sacs.
TNkPV B=
Tk
PV
N
B
=
( )( ) 2
1314
Oofmolecules107.214.0109.1 ×=×=N
( ) ( )[ ]
( )( )K310KJ1038.1
m10125.0Pa1000.1
23
33
3
45
−
−
×
××
=
π
airofmolecules109.1 14
×=N

19. Conceptual Example 3 Soda Bubbles on the Rise
Watch the bubbles rise in a glass of soda. If you look carefully, you’ll
see them grow in size as they move upward, often doubling in volume
by the time they reach the surface. Why does the bubble grow as it
ascends?

20. Consider a sample of an ideal gas that is taken from an initial to a final
state, with the amount of the gas also changing.
nRTPV =
ii
ii
ff
ff
Tn
VP
Tn
VP
=constant== R
nT
PV
Other Gas Laws
Constant T, constant n: iiff VPVP = Boyle’s law
Constant P, constant n:
i
i
f
f
T
V
T
V
= Charles’ law
Constant P, constant T:
i
i
f
f
n
V
n
V
= Avogadro’s law
Constant V, constant n:
i
i
f
f
T
P
T
P
= Gay-Lussac’s law

21. 14.2.1. Using the ideal gas law, estimate the approximate number of
air particles within an otherwise empty room that has a height of
2.5 m, a width of 4.0 m, and a length of 5.0 m.
a) 1.2 × 1027
b) 6.8 × 1025
c) 3.0 × 1026
d) 2.5 × 1028
e) 9.1 × 1024

22. 14.2.2. An ideal gas is enclosed within a container by a moveable
piston. If the final temperature is two times the initial
temperature and the volume is reduced to one-fourth of its initial
value, what will the final pressure of the gas be relative to its
initial pressure, P1?
a) 8P1
b) 4P1
c) 2P1
d) P1/2
e) P1/4

23. 14.2.3. Consider a commercial sightseeing hot air balloon that
carries a basket with more than 20 passengers. Assume that
balloon contains 1.5 × 104
m3
of air. Estimate the order of
magnitude of the number of air molecules inside the balloon.
a) 1023
b) 1029
c) 1035
d) 1018
e) 104

24. Chapter 14:
Ideal Gas Law & Kinetic Theory
Section 3:
The Kinetic Theory of Gases

25. Postulates of Kinetic(-Molecular) Theory
 All gases are made up of particles
 Usually molecules
 The particles are in constant, random
motion, colliding with each other and
with the walls of the container.
 All collisions are perfectly elastic
 Volume of the particles is insignificant
 There are no interactions between
particles (attraction/repulsion)
 The average kinetic energy of the
particles is a function of only absolute
temperature

26. THE DISTRIBUTION OF MOLECULAR SPEEDS

27. collisionssuccessivebetweenTime
momentumInitial-momentumFinal
F =
( )
t
mv
t
v
mmaF
∆
∆
=
∆
∆
==∑
Kinetic Theory
L
mv2
−
=
( ) ( )
vL
mvmv
2
F
+−−
=

28. L
mv
F
2
=
For a single molecule, the average force is:
For N molecules in 3 dimensions, the average force is:














=
L
vmN
F
2
3 root-mean-square
speed
A
F
P =
volume
Kinetic Theory
2
L
F
=














= 3
2
3 L
vmN

29. 













=
V
vmN
P
2
3
( )2
3
1
rmsmvNPV =
TNkB K
TkB2
3
K =
Kinetic Theory
( )2
2
1
3
2
rmsmvN=
µ
Tk
M
RT
v B
rms
33
==
Molar mass

30. Conceptual Example 5 Does a Single Particle Have a Temperature?
Each particle in a gas has kinetic energy. On the previous page, we have
established the relationship between the average kinetic energy per particle
and the temperature of an ideal gas.
Is it valid, then, to conclude that a single particle has a temperature?
No, the temperature relates to the average
of the whole sample, as there is one temperature
for the sample.

31. Example 6 The Speed of Molecules in Air
Air is primarily a mixture of nitrogen N2 molecules (molecular mass
28.0 u) and oxygen O2 molecules (molecular mass 32.0 u). Assume
that each behaves as an ideal gas and determine the rms speeds
of the nitrogen and oxygen molecules when the temperature of the air
is 293K.
M
RT
vrms
3
=
( )( )
molM
RT
vrms
kg8002.0
K293KmolJ31.833 ⋅
==
For nitrogen…
( )( )
molM
RT
vrms
kg2003.0
K293KmolJ31.833 ⋅
==
For oxygen…
sm511=
sm478=

32. Tkmv Brms 2
32
2
1
K ==
nRTkTNU 2
3
2
3
==
Internal Energy of a Monatomic Ideal Gas

33. 14.3.1. Two sealed containers, labeled A and B as shown, are at the same
temperature and each contain the same number of moles of an ideal monatomic
gas. Which one of the following statements concerning these containers is true?
a) The rms speed of the atoms in the gas is
greater in B than in A.
b) The frequency of collisions of the atoms
with the walls of container B are greater than
that for container A.
c) The kinetic energy of the atoms in the gas is greater in B than in A.
d) The pressure within container B is less than the pressure inside container A.
e) The force that the atoms exert on the walls of container B are greater than in for
those in container A.

34. 14.3.2. Two identical, sealed containers have the same volume. Both containers are filled
with the same number of moles of gas at the same temperature and pressure. One of
the containers is filled with helium gas and the other is filled with neon gas. Which
one of the following statements concerning this situation is true?
a) The speed of each of the helium atoms is the same value, but this speed is different
than that of the neon atoms.
b) The average kinetic energy of the neon atoms is greater than that of the helium atoms.
c) The pressure within the container of helium is less than the pressure in the container
of neon.
d) The internal energy of the neon gas is greater than the internal energy of the helium
gas.
e) The rms speed of the neon atoms is less than that of the helium atoms.

35. 14.3.3. A monatomic gas is stored in a container with a constant
volume. When the temperature of the gas is T, the rms speed of
the atoms is vrms. What is the rms speed when the gas temperature
is increased to 3T?
a) vrms/9
b)
c) 3vrms
d) vrms
e) 9vrms
rms / 3v
3

36. 14.3.4. Closed containers A and B both contain helium gas at the same
temperature. There are n atoms in container A and 2n atoms in container B.
At time t = 0 s, all of the helium atoms have the same kinetic energy. The
atoms have collisions with each other and with the walls of the container.
After a long time has passed, which of the following statements will be true?
a) The atoms in both containers have the same kinetic energies they had at time t =
0 s.
b) The atoms in both containers have a wide range of speeds, but the distributions
of speeds are the same for both A and B.
c) The average kinetic energy for atoms in container B is higher than that for
container A.
d) The average kinetic energy for atoms in container A is higher than that for
container B.
e) The atoms in both containers have a wide range of speeds, but the distributions
of speeds has a greater range for container B than that for container A.

37. 14.3.5. Assume that you have a container with 0.25 kg of helium
gas at 20 °C. How much energy must be added to the gas to
increase its temperature to 70 °C?
a) 4 × 104
J
b) 2 × 105
J
c) 5 × 106
J
d) 1 × 107
J
e) 3 × 108
J

38. Chapter 14:
Ideal Gas Law & Kinetic Theory
Section 4:
Diffusion

39. The process in which molecules move from a region of higher concentration
to one of lower concentration is called diffusion.
Diffusion

40. Conceptual Example 7 Why Diffusion is Relatively Slow
A gas molecule has a translational rms speed of hundreds of meters
per second at room temperature. At such speed, a molecule could
travel across an ordinary room in just a fraction of a second. Yet, it
often takes several seconds, and sometimes minutes, for the fragrance
of a perfume to reach the other side of the room. Why does it take so
long?

41. A Transdermal Patch

43. ( )
L
tCDA
m
∆
=
FICK’S LAW OF DIFFUSION
The mass m of solute that diffuses in a time t through a solvent contained
in a channel of length L and cross sectional area A is
concentration gradient
between ends
diffusion
constant
SI Units for the Diffusion Constant: m2
/s

44. Example 8 Water Given Off by Plant Leaves
Large amounts of water can be given off by
plants. Inside the leaf, water passes from the
liquid phase to the vapor phase at the walls
of the mesophyll cells.
The diffusion constant for water is 2.4x10-5
m2
/s.
A stomatal pore has a cross sectional area of
about 8.0x10-11
m2
and a length of about
2.5x10-5
m. The concentration on the interior
side of the pore is roughly 0.022 kg/m3
, while
that on the outside is approximately 0.011 kg/m3
.
Determine the mass of water that passes through
the stomatal pore in one hour.

45. ( )
( )( )( )( )
kg100.3
m102.5
s3600mkg011.0mkg022.0m100.8sm104.2
9
5-
3321125
−
−−
×=
×
−××
=
∆
=
L
tCDA
m

46. 14.4.1. Sealed containers with a valve in the middle contain equal amounts of two different
monatomic gases at room temperature as shown. A few of the gas atoms are illustrated with
arrows representing their velocities. Which of the following statements concerning the gases
after the valve has been opened is correct?
a) Because there is no pressure
difference, the two gases will
remain separated for the most
part. Only a few atoms of each
gas will be exchanged.
b) As soon as the valve is opened,
the two gases will mix completely.
c) The two gases will collide in the narrow tube and be scattered back into their original chambers,
so no mixing will occur.
d) After a relatively long period of time, the two gases will be well mixed in both containers.
e) The lighter of the two gases will occupy both spherical containers, but the heavier gas atom will
mostly remain in their original container.