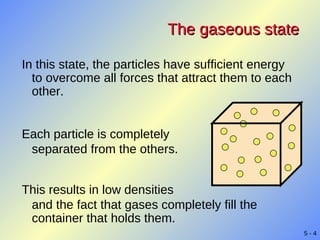
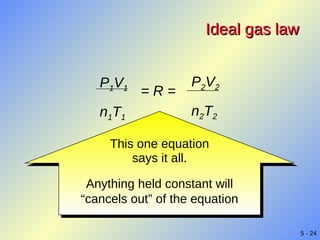
- Gases exhibit behaviors described by gas laws such as Boyle's law, Charles' law, and Gay-Lussac's law. The ideal gas law combines several gas laws into a single equation relating pressure, volume, temperature, and moles of gas. - Real gases deviate from ideal gas behavior due to intermolecular forces and molecular size. The van der Waals equation accounts for these factors. - Kinetic molecular theory explains gas properties in terms of the high-speed motion and infrequent collisions of molecules separated by large distances.

2. Elemental states at 25 o C He Rn Xe I Kr Br Se Ar Cl S Ne F O P N C H Li Na Cs Rb K Tl Hg Au Hf Ls Ba Fr Pt Ir Os Re W Ta Po Bi Pb Be Mg Sr Ca Cd Ag Zr Y Pd Rh Ru Tc Mo Nb Ac Ra Zn Cu Ti Sc Ni Co Fe Mn Cr V In Sb Sn Ga Ge Al Gd Cm Tb Bk Sm Pu Eu Am Nd U Pm Np Ce Th Pr Pa Yb No Lu Lr Er Fm Tm Md Dy Cf Ho Es At Te As Si B 5 - 2 Solid Liquid Gas

6. Barometer Device used to measure atmospheric pressure. One atm 760 mm Hg 29.9 in Hg vacuum

11. Boyle’s law Increasing the pressure on a sample on gas decreases it volume at constant temperature. Note the effect here as weight is added.

12. Charles’ law The volume of a gas is directly proportional to the absolute temperature (K). V T = k or V 1 V 2 T 1 T 2 Pressure and number of moles must be held constant! =

13. Charles’ law When you heat a sample of a gas, its volume increases. The pressure and number of moles must be held constant.

14. Charles’ Law Placing an air filled balloon near liquid nitrogen (77 K) will cause the volume to be reduced. Pressure and the number of moles are constant.

18. Avogadro’s law If you have more moles of a gas, it takes up more space at the same temperature and pressure.

22. Ideal gas law PV nT ( 1 atm ) ( 22.4 L ) ( 1 mol ) ( 273.15 K) R = = 0.08206 atm L mol -1 K -1 R = R can be determined from standard conditions.

24. Ideal gas law P 1 V 1 n 1 T 1 = R = P 2 V 2 n 2 T 2 This one equation says it all. Anything held constant will “ cancels out” of the equation

26. Example If a gas has a volume of 3.0 liters at 250 K, what volume will it have at 450 K ? P 1 V 1 n 1 T 1 = P 2 V 2 n 2 T 2 V 1 T 1 = V 2 T 2 Cancel P and n They don’t change We end up with Charles’ Law

33. Diffusion

37. Kinetic-molecular theory O 2 at 25 o C O 2 at 700 o C H 2 at 25 o C Average speed Fraction having each speed 0 500 1000 1500 2000 2500 3000 Molecular speed (m/s)

38. Real gases We can plot the compressibility factor ( PV/nRT ) for gases. If the gas is ideal, it should always give a value of 1. Obviously, none of these gases are ‘ideal.’ Compressibility factor 0 5 10 Pressure, atm H 2 N 2 CH 4 C 2 H 4 NH 3