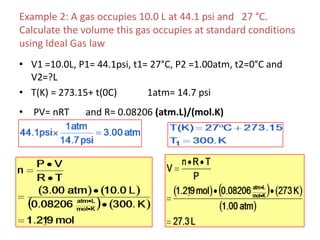
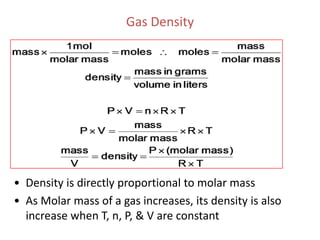
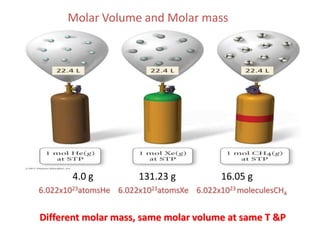
1) The document discusses the ideal gas law (PV=nRT) and its applications in calculating things like moles of gas, volume at different conditions, density, and molar mass. 2) Key variables in the ideal gas law are defined such as pressure (P), volume (V), moles of gas (n), temperature (T), and the gas constant (R). 3) Standard temperature and pressure conditions are defined as 0°C and 1 atmosphere, where the molar volume of a gas is 22.4 L.

1. Ideal Gas LawPV = nRTApplication of PV=nRTDensity Molecular Mass

2. Ideal Gas LawBy combining the gas laws we can write a general equationwhereP is the pressure , V is the volume, n is the amount of gas in mole, and T(K) is the temperature

3. The constant is shown byR, gas Law constant . The value of R, depends on the units of P & VR =0.08206[(atm.L)/(mol.K)], when P is in atm and V is in LExample: How many moles of gas are in a basketball with total pressure 24.3 psi, volume of 3.24 L at 25°C?V = 3.24 L, P = 24.3 psi, t = 25 °C and n=? Mol

4. T(K) = 273.15+ t(0C) 1atm= 14.7 psi

5. R= 0.08206 (atm.L)/(mol.K) 21Knowing PV= nRT, Rearrange the equation to :3

6. Standard ConditionsThe Standard Temperature & pressure, STP is whenStandard pressure = 1 atmStandard temperature = 273 K, 0 °C1 mole of any gas at STP condition has a volume equal to 22.4 L

7. Molar Volume = Volume of 1 mole of a gasSolving the ideal gas equation for the volume of 1 mole of any gas at STP gives a volume of 22.4 L1 mole of a gas has 6.022x1023 molecules of gas6.022x1023 molecules of gas occupies a volume of 22.4L at STPMolar volume of a gas at STP is 22.4 LOne mole of different gases have the same volume at same temperature and pressure, but have different masses

8. Molar Volume and Molar mass4.0 g 131.23 g 16.05 g6.022x1023atomsHe6.022x1023atomsXe 6.022x1023 moleculesCH4Different molar mass, same molar volume at same T &P

9. Example 2: A gas occupies 10.0 L at 44.1 psi and 27 °C. Calculate the volume this gas occupies at standard conditions using Ideal Gas lawV1 =10.0L, P1= 44.1psi, t1= 27°C, P2 =1.00atm, t2=0°C and V2=?LT(K) = 273.15+ t(0C) 1atm= 14.7 psi PV= nRT and R= 0.08206 (atm.L)/(mol.K)

10. Example 2: Calculate the volume occupied by 637 g of SO2 (MM 64.07) at 6.08 x 104 mmHg and –23 °CmSO2 = 637 g, P = 6.08 x 104 mmHg, t= −23 °C, &V=?L1 atm= 760 mmHg 1 mole of SO2 = 64.07 g SO2 T(K) = 273.15+ t(0C) PV= nRT & R= 0.08206 (atm.L)/(mol.K)

11. Density at Standard ConditionsDensity is the ratio of mass to volumeDensity of a gas is generally given in g/LThe mass of 1 mole = molar massThe volume of 1 mole at STP = 22.4 LExample: Calculate the density of N2(g) at STP

12. Gas DensityDensity is directly proportional to molar mass

13. As Molar mass of a gas increases, its density is also increase when T, n, P, & V are constant Example : Calculate the density of N2 at 125°C and 755 mmHg P = 755 mmHg, t = 125 °C, dN2 = ?g/L

14. 1 atm =760 mmHg, 1mole N2=28.0g N2, T(k) = 273.15 + t(0C)Example2: Calculate the density of a gas at 775 torr and 27 °C if 0.250 moles weighs 9.988 g m = 9.988g, n = 0.250 mol, P = 1.0197 atm, T = 300.K Density= ?g/L1atm =760 mmHg, T(K)=273.15+t(0C), PV=nRT, & d=(m/v)Molar Mass of a GasOne of the methods chemists use to determine the molar mass of an unknown substance is to heat a weighed sample until it becomes a gas, measure the temperature, pressure, and volume, and use the ideal gas law to calculate the number of moles, thenExample: Calculate the molar mass of a gas with mass 0.311 g that has a volume of 0.225 L at 55°C and 886 mmHgm=0.311g, V=0.225L, P=1.1658 atm, T=328 K, molar mass= ? g/mol1atm =760 mmHg, T(K)=273.15+t(0C), PV=nRT, & Molar Mass =(mass/n) g/mole

15. What is the molar mass of a gas if 12.0 g occupies 197 L at 3.80 x 102 torr and 127 °C?m = 12.0g, V = 197 L, P = 0.50 atm, T =400 K, molar mass= ?g/mol1atm =760 mmHg, T(K)=273.15+t(0C), PV=nRT, & Molar Mass =(mass/n) g/mole