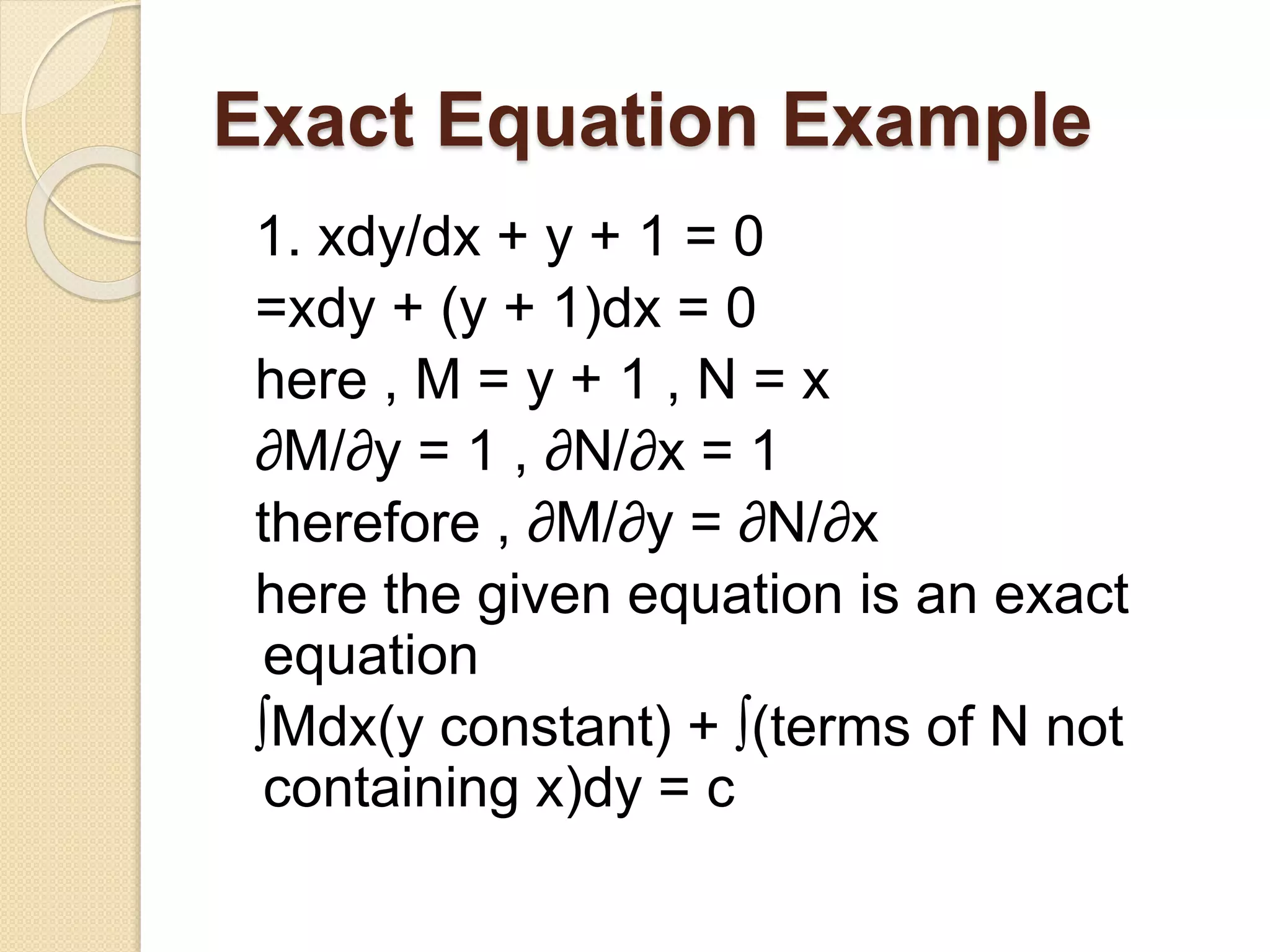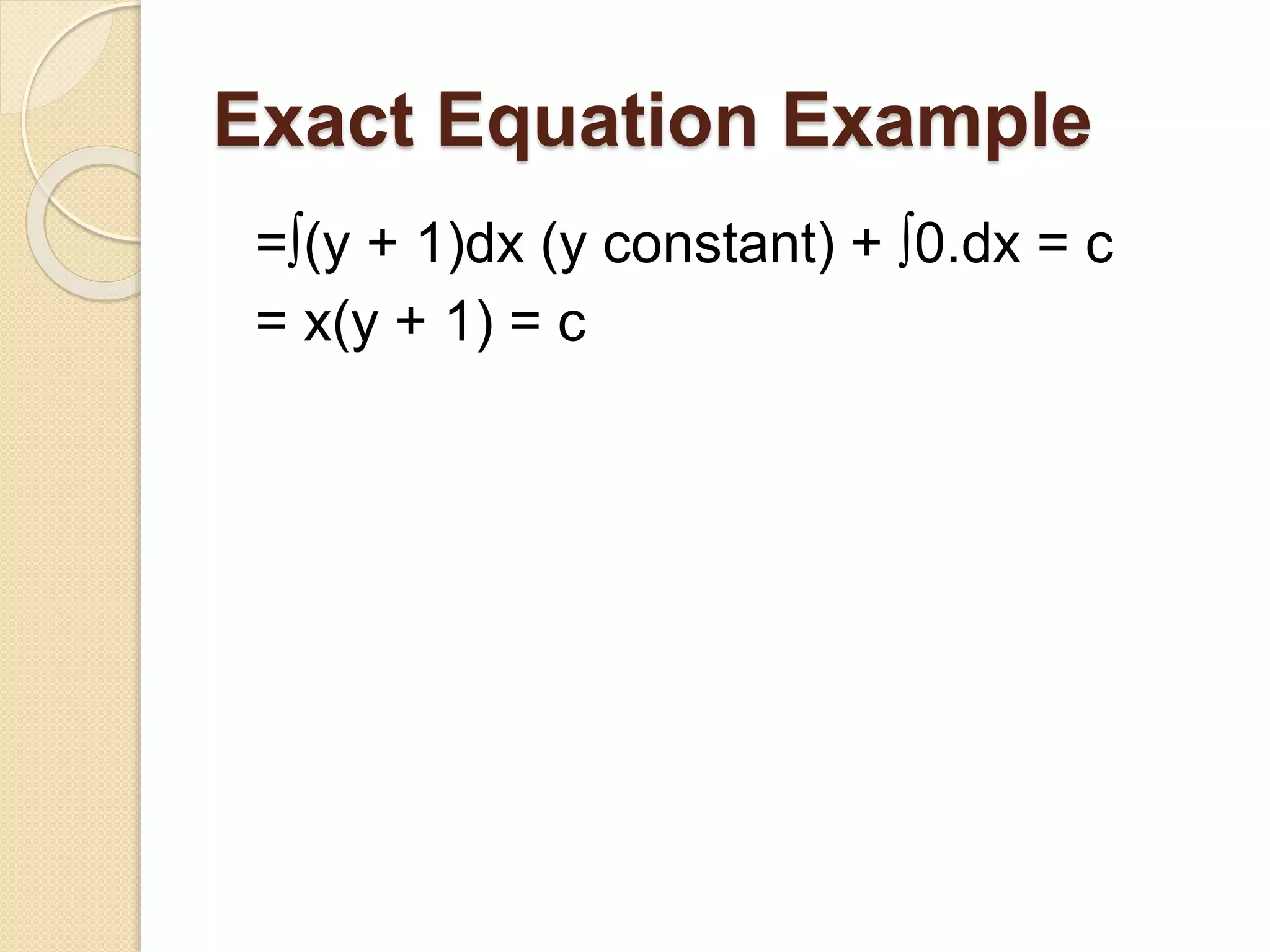1) A differential equation contains an independent variable (x), a dependent variable (y), and the derivative of the dependent variable with respect to the independent variable (dy/dx). 2) The order of a differential equation refers to the highest order derivative present. For example, an equation containing dy/dx would be first order, while one containing d2y/dx2 would be second order. 3) The degree of a differential equation refers to the highest power of the highest order derivative. For example, an equation containing (d2y/dx) would be degree 1, while one containing (d2y/dx)2 would be degree 2. 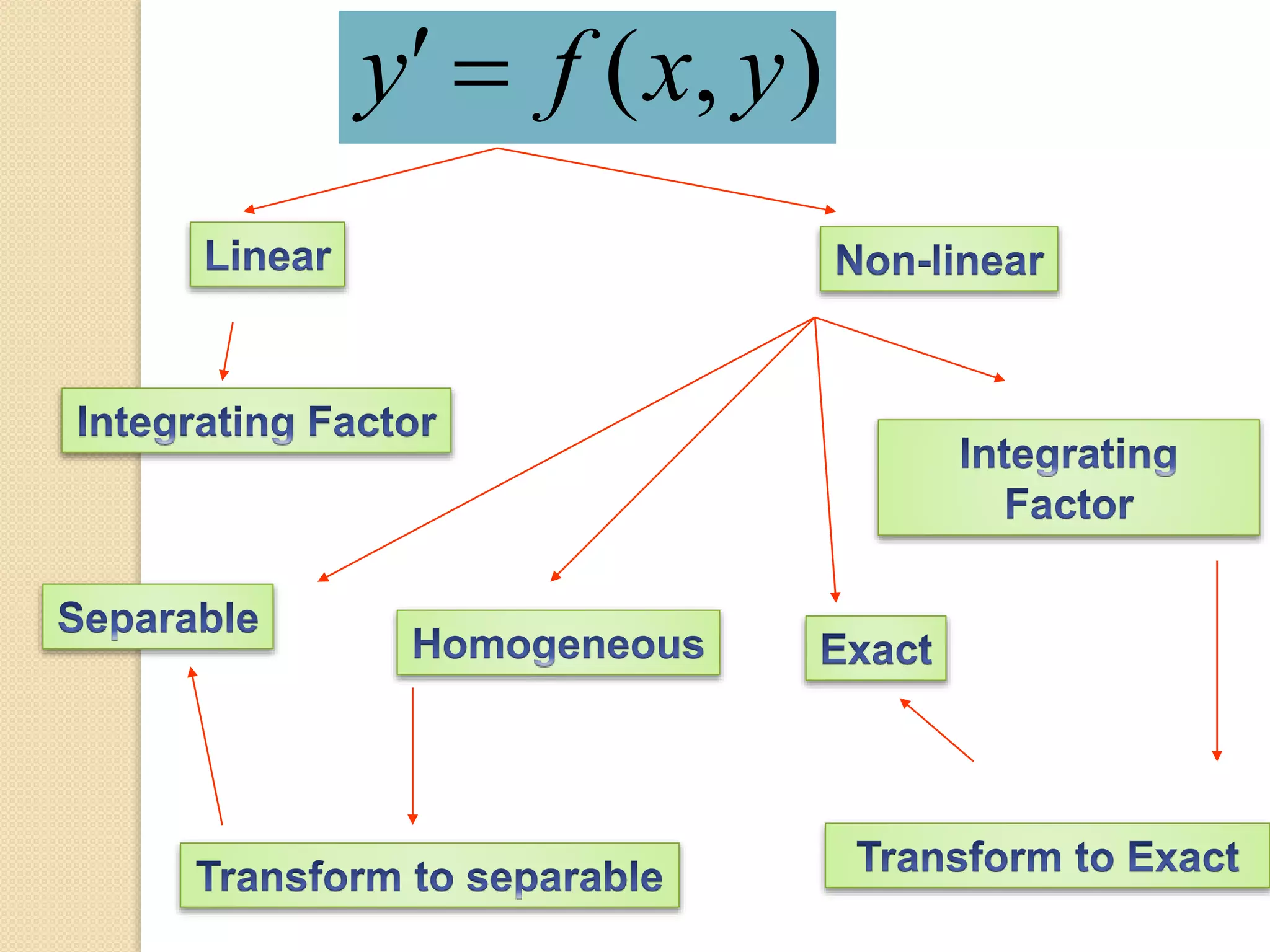4) There are several methods for solving first

1. What is Differential equation?
 If y is a function of x, then we denote it
as y = f(x). Here x is called an
independent variable and y is called a
dependent variable.
 If there is a equation dy/dx = g(x) ,then
this equation contains the variable x
and derivative of y w.r.t x. This type of
an equation is known as a Differential
Equation.

2. Order of Differential Equation
 Order of the highest order derivative of
the dependent variable with respect to
the independent variable occurring in
a given differential equation is called
the order of differential equation.
 E.g. – 1st order equation
 2nd order equation

3. Degree of Differential Equation
 When a differential equation is in a
polynomial form in derivatives, the
highest power of the highest order
derivative occuring in the differential
equation is called the degree of the
differential equation.
 E.g. – Degree – 1 ,(d²y/dx) + dy/dx = 0
Degree – 2 , (d²y/dx)² + dy/dx = 0

4. Solution of differential
equations of the first order
and first degree
 Differential equations of 1st order can
be solved by many methods ,some of
the methods are as follows :-
1. Variable Separable Method
2. Exact equation method
3. Homogenous equation method
4. Linear equation method

5. Solution of differential
equations of the first order
and first degree
5. Non-Linear Equation method
(Bernoulli's equation)
6. Non-Exact Equation method

6. ( , )y f x y 

7. Important Forms of the
method
 Here are some important forms of the
method through which we can know
the form of equation and then use or
apply the method which is required :-
1. Variable Separable method –
Equation is in the form of :
dy/dx = M(x)/N(y) or
dy/dx = M(x)N(y)

8. Important Forms of the
method
2. Exact equation method – equation
is in the form of :
Mdx + Ndy = 0 --- 1
If , ∂M/∂y = ∂N/∂x
Then the above equation 1 is Exact
equation
3. Homogenous equation method -
equation is in the form of :
dy/dx = x²y + x³y + xy²/x³ - y³ (Example)

9. Important Forms of the
method
4. Linear equation method - equation
is in the form of :
Form -1 : dy/dx + Py = Q (x form)
Form - 2 : dx/dy + Px = Q (y form)
5. Non-Linear Equation method
(Bernoulli's equation) - equation is in
the form of :
Dy/dx – 2ytanx = y²tan²x (Example)

10. Important Forms of the
method
6. Non-Exact Equation method -
equation is in the form of :
Type – 1 : Mdx + Ndy = 0
F(x) = 1/N (∂M/∂y - ∂N/∂x) (x form)
Type – 2 : Mdx + Ndy = 0
F(y) = 1/M (∂N/∂x - ∂M/∂y)

11. 1st Order DE - Homogeneous Equations
Homogeneous Function
f (x,y) is called homogenous of degree n if :
   y,xfy,xf n
 
Examples:
  yxxy,xf 34
  homogeneous of degree 4
       
   yxfyxx
yxxyxf
,
,
4344
34




  yxxyxf cossin, 2
  non-homogeneous
       
   
 yxf
yxx
yxxyxf
n
,
cossin
cossin,
22
2







12. 1st Order DE - Homogeneous Equations
The differential equation M(x,y)dx + N(x,y)dy = 0 is homogeneous if M(x,y) and
N(x,y) are homogeneous and of the same degree
Solution :
1. Use the transformation to : dvxdxvdyvxy 
2. The equation become separable equation:
    0,,  dvvxQdxvxP
3. Use solution method for separable equation
 
 
 
 
Cdv
vg
vg
dx
xf
xf
  1
2
2
1
4. After integrating, v is replaced by y/x

13. Variable – separable example
1. dy/dx = x.y
=dy/y = xdx
=∫dy/y = ∫xdx
=logy = x²/2 + c

14. Exact Equation Example
1. xdy/dx + y + 1 = 0
=xdy + (y + 1)dx = 0
here , M = y + 1 , N = x
∂M/∂y = 1 , ∂N/∂x = 1
therefore , ∂M/∂y = ∂N/∂x
here the given equation is an exact
equation
∫Mdx(y constant) + ∫(terms of N not
containing x)dy = c

15. Exact Equation Example
=∫(y + 1)dx (y constant) + ∫0.dx = c
= x(y + 1) = c