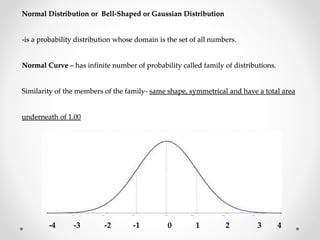
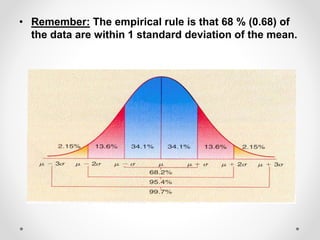
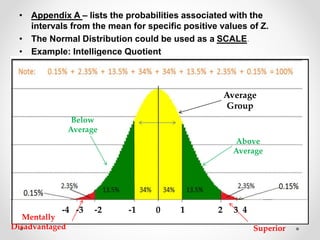
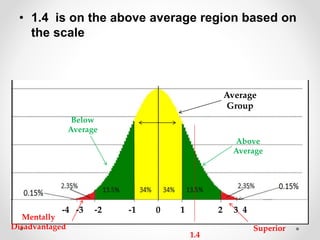
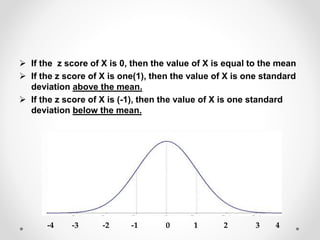
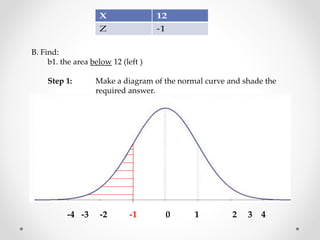
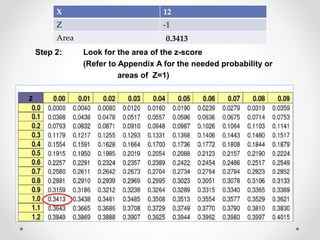
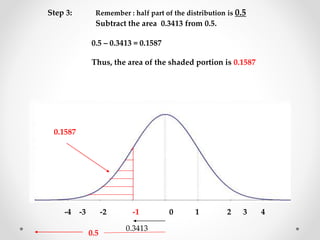
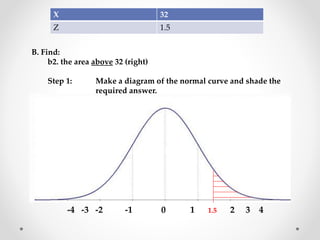
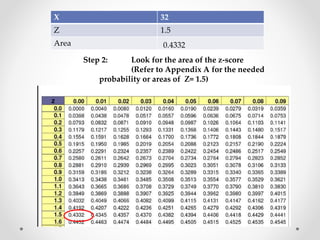
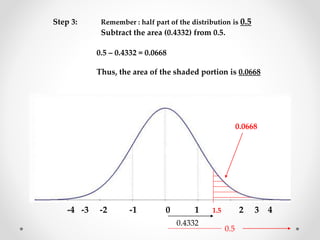
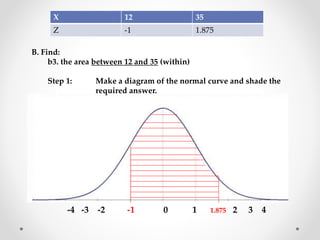
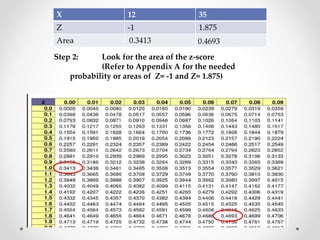
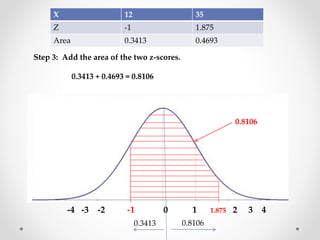
The document discusses standard scores and the normal distribution curve. It defines key terms like the normal curve, z-scores, mean, and standard deviation. It also provides examples of how to convert raw scores to z-scores and find the probability of scores relative to the mean using the normal curve. Areas under the normal curve can be calculated using z-score values from standard normal distribution tables in an appendix.

1. Standard Scores
and the Normal
Curve
Reporters:
Grace V. Domingo
Elizabeth Aireen V. Villanueva

2. Normal Distribution or Bell-Shaped or Gaussian Distribution
-is a probability distribution whose domain is the set of all numbers.
Normal Curve – has infinite number of probability called family of distributions.
Similarity of the members of the family- same shape, symmetrical and have a total area
underneath of 1.00
-4 -3 -2 -1 0 1 2 3 4

3. • Difference: location of the midpoint (determined by x̅ )
and the variability of scores around the midpoint (
determined by S)
• Z-score is the number of standard deviations from the
mean a data point is. But more technically it’s a measure
of how many standard deviations below or above the
population mean a raw score is. A z-score is also known
as a standard score and it can be placed on a normal
distribution curve.
• To convert any X value to a standard score:
Where:
Z- the z score
X- the raw score
x̅ - the mean
S- standard deviation

4. • Remember: The empirical rule is that 68 % (0.68) of
the data are within 1 standard deviation of the mean.

5. • Appendix A – lists the probabilities associated with the
intervals from the mean for specific positive values of Z.
• The Normal Distribution could be used as a SCALE.
• Example: Intelligence Quotient
Average
Group
Above
Average
Superior
Below
Average
Mentally
Disadvantaged
-4 -3 -2 -1 0 1 2 3 4

6. • Convert the following score to Z score and locate
them in the Normal distribution.
• Given: X=79, x̅ = 72, S=5
• Using the formula:
= 79 – 72 = 1.4
5

7. • 1.4 is on the above average region based on
the scale
Average
Group
Above
Average
Superior
Below
Average
Mentally
Disadvantaged
1.4
-4 -3 -2 -1 0 1 2 3 4

8. • The Z- formula: shows a random variable is standardized by
subtracting the mean of the distribution from the value being
standardized, and then dividing this difference by the standard
deviation. Once standardized, a normally distributed random variable
has a mean of zero and a standard deviation of one.
• The z scores are important because they tell us how far a value is from
the mean when we standardize a random variable.
Where:
Z- the z score
X- the raw score or the value that is
being standardized
x̅ - the mean of the distribution
S- standard deviation

9.  If the z score of X is 0, then the value of X is equal to the mean
 If the z score of X is one(1), then the value of X is one standard
deviation above the mean.
 If the z score of X is (-1), then the value of X is one standard
deviation below the mean.
-4 -3 -2 -1 0 1 2 3 4

10. • Finding the areas under the normal curve:
Given the normal distribution with a x̅ =20 and S= 8
a. Convert the following to Z-score.
12, 32, 35, 31
Using the formula:

11. B. Find:
b1. the area below 12 (left )
Step 1: Make a diagram of the normal curve and shade the
required answer.
-4 -3 -2 -1 0 1 2 3 4

12. Step 2: Look for the area of the z-score
(Refer to Appendix A for the needed probability or
areas of Z=1)
X 12
Z -1
Area 0.3413

13. -4 -3 -2 -1 0 1 2 3 4
Step 3: Remember : half part of the distribution is 0.5
Subtract the area 0.3413 from 0.5.
0.3413
0.5
0.1587
0.5 – 0.3413 = 0.1587
Thus, the area of the shaded portion is 0.1587

14. B. Find:
b2. the area above 32 (right)
Step 1: Make a diagram of the normal curve and shade the
required answer.
-4 -3 -2 -1 0 1 1.5 2 3 4
X 32
Z 1.5

15. Step 2: Look for the area of the z-score
(Refer to Appendix A for the needed
probability or areas of Z= 1.5)
X 32
Z 1.5
Area 0.4332

16. Step 3: Remember : half part of the distribution is 0.5
Subtract the area (0.4332) from 0.5.
-4 -3 -2 -1 0 1 1.5 2 3 4
0.4332
0.5
0.5 – 0.4332 = 0.0668
Thus, the area of the shaded portion is 0.0668
0.0668

17. B. Find:
b3. the area between 12 and 35 (within)
Step 1: Make a diagram of the normal curve and shade the
required answer.
-4 -3 -2 -1 0 1 1.875 2 3 4
X 12 35
Z -1 1.875

18. Step 2: Look for the area of the z-score
(Refer to Appendix A for the needed
probability or areas of Z= -1 and Z= 1.875)
X 12 35
Z -1 1.875
Area 0.3413 0.4693

19. Step 3: Add the area of the two z-scores.
0.3413 + 0.4693 = 0.8106
-4 -3 -2 -1 0 1 1.875 2 3 4
X 12 35
Z -1 1.875
Area 0.3413 0.4693
0.8106
0.3413 0.8106