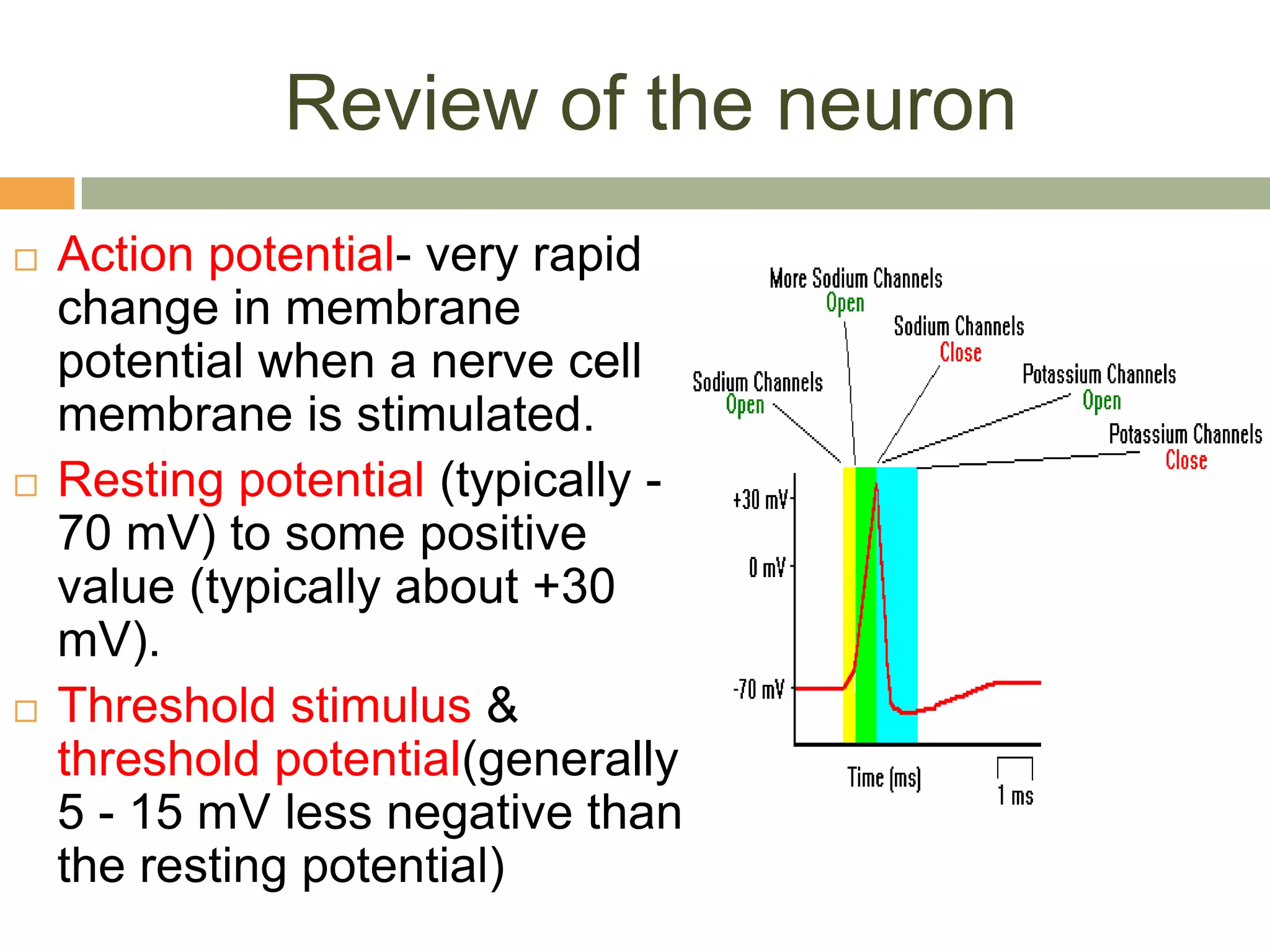
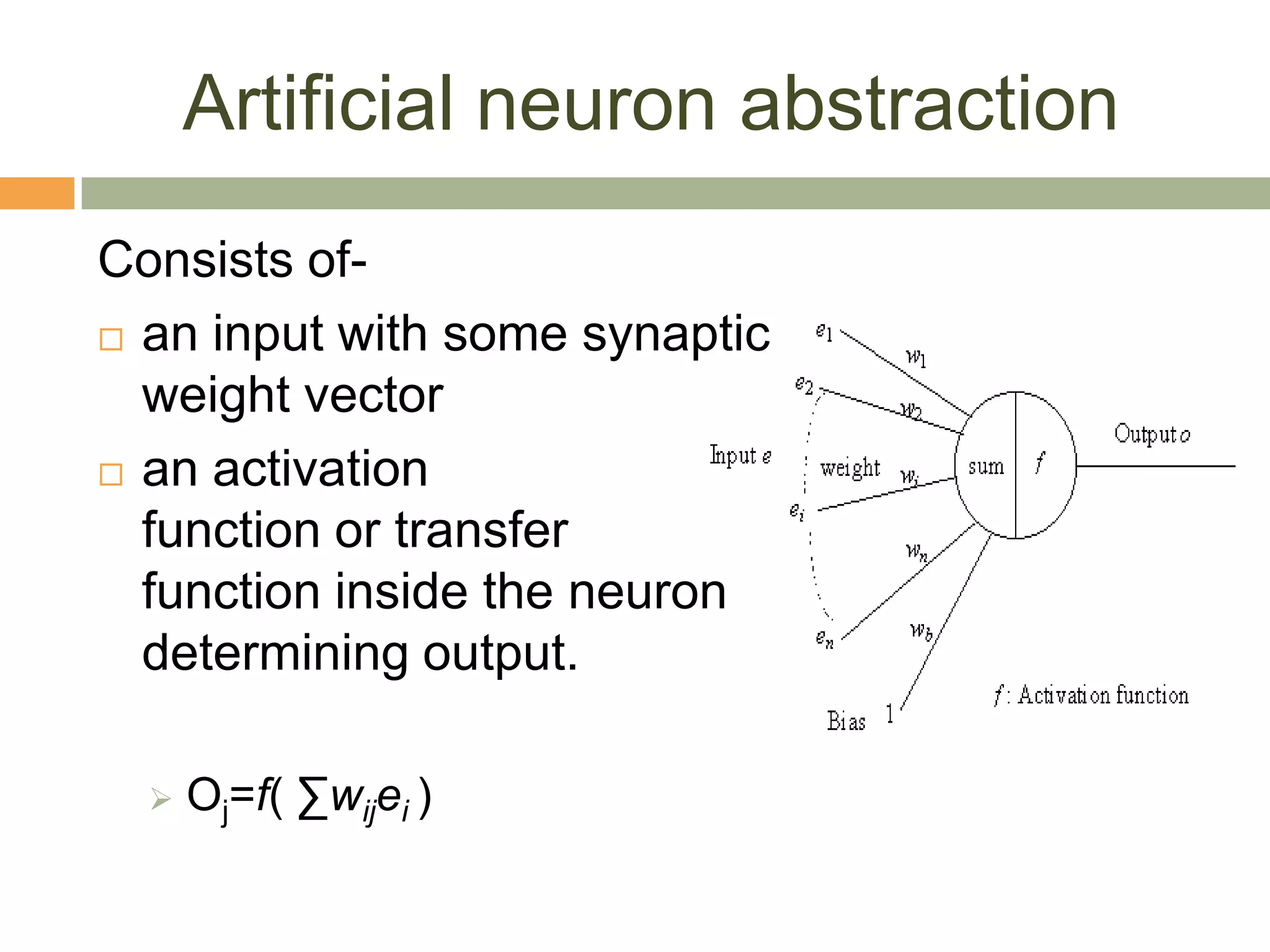
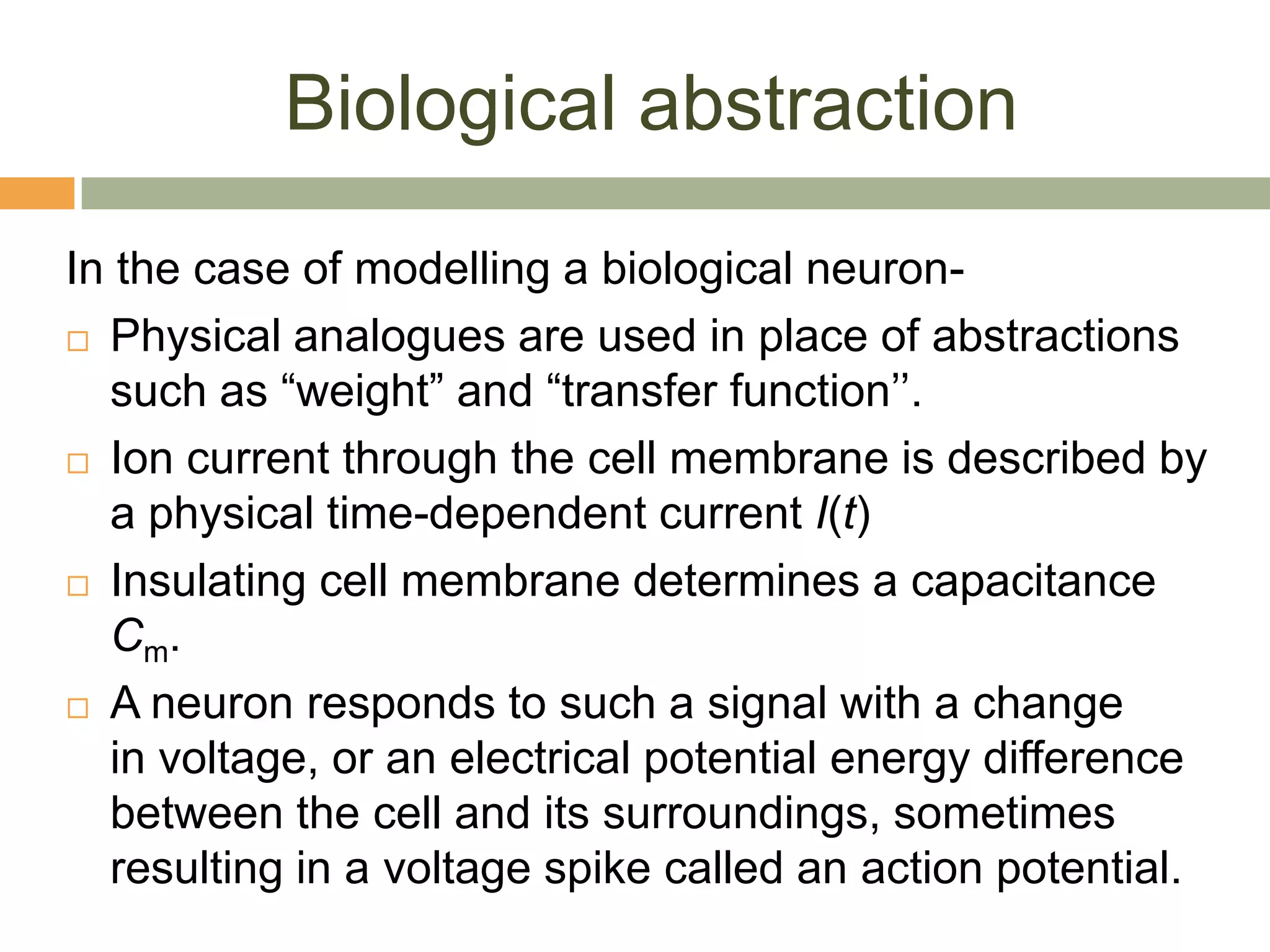
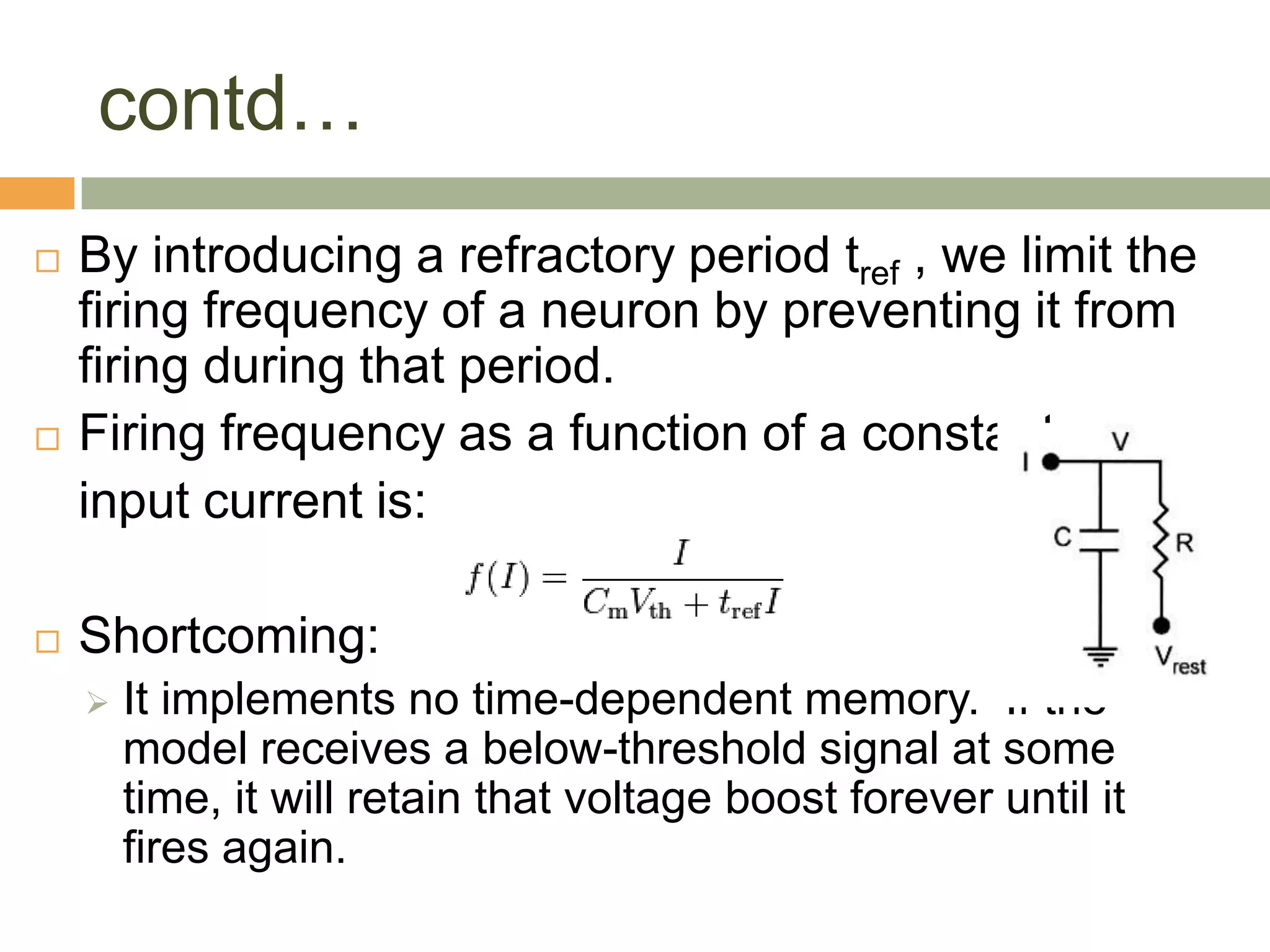
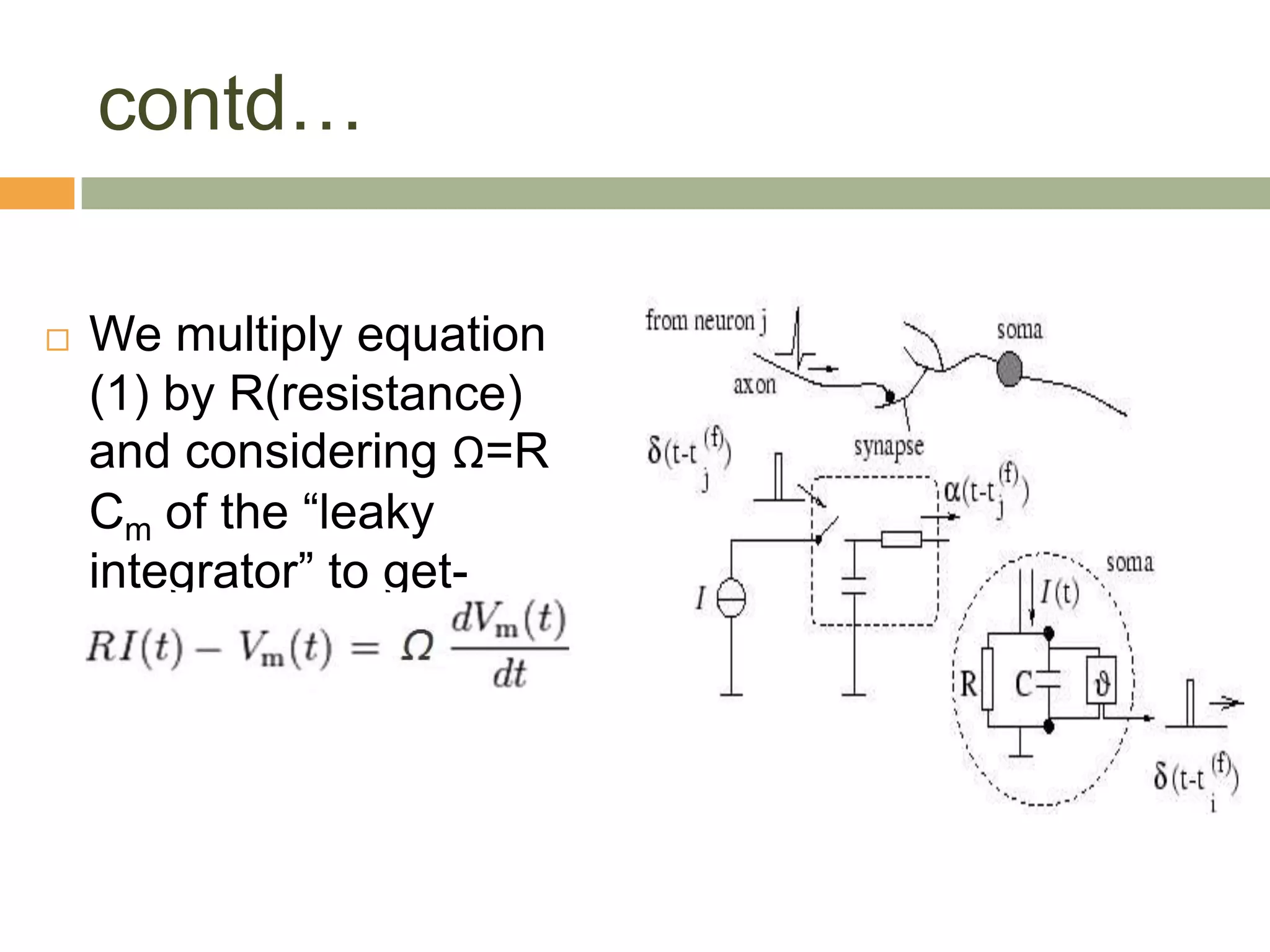
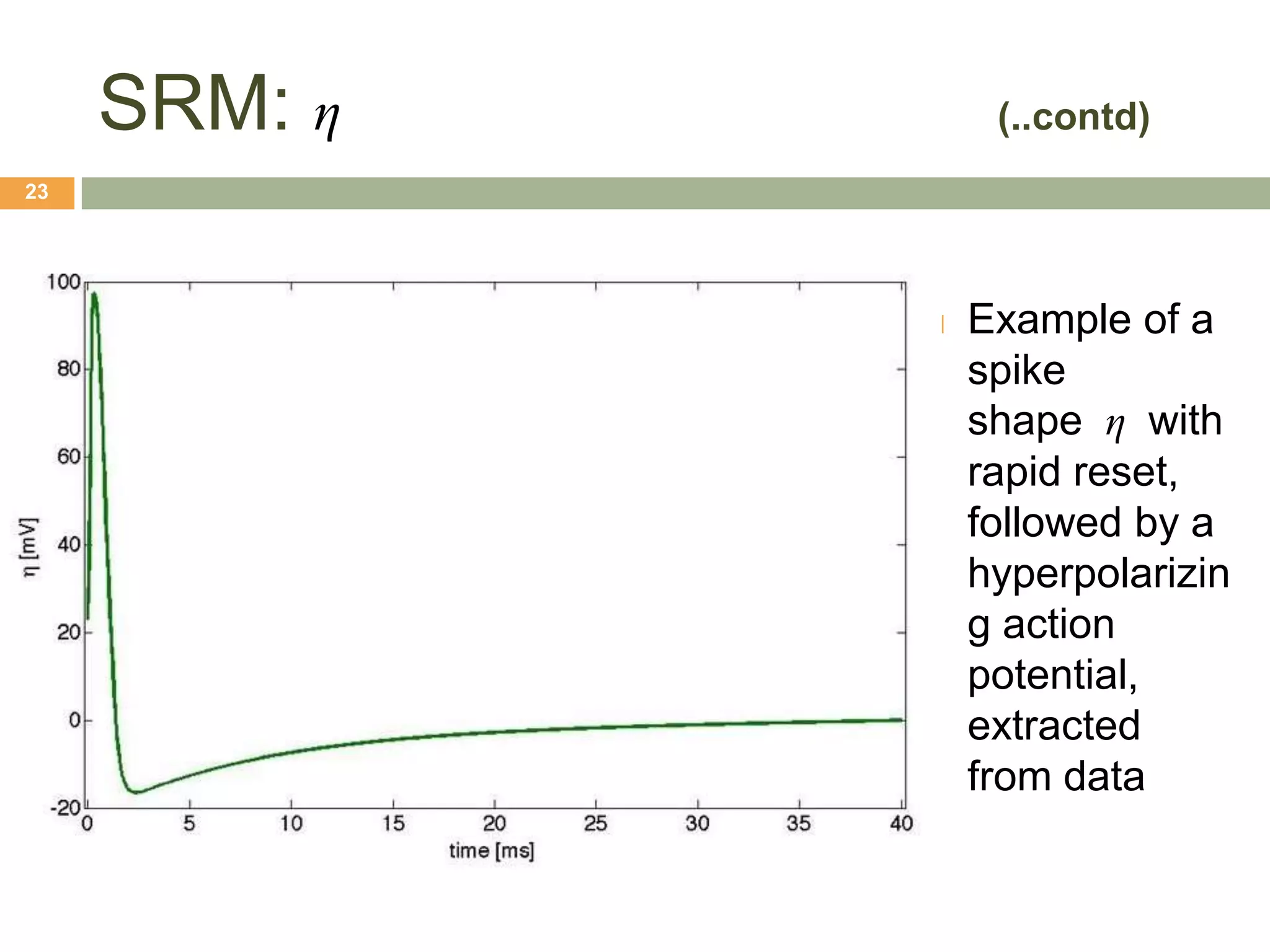
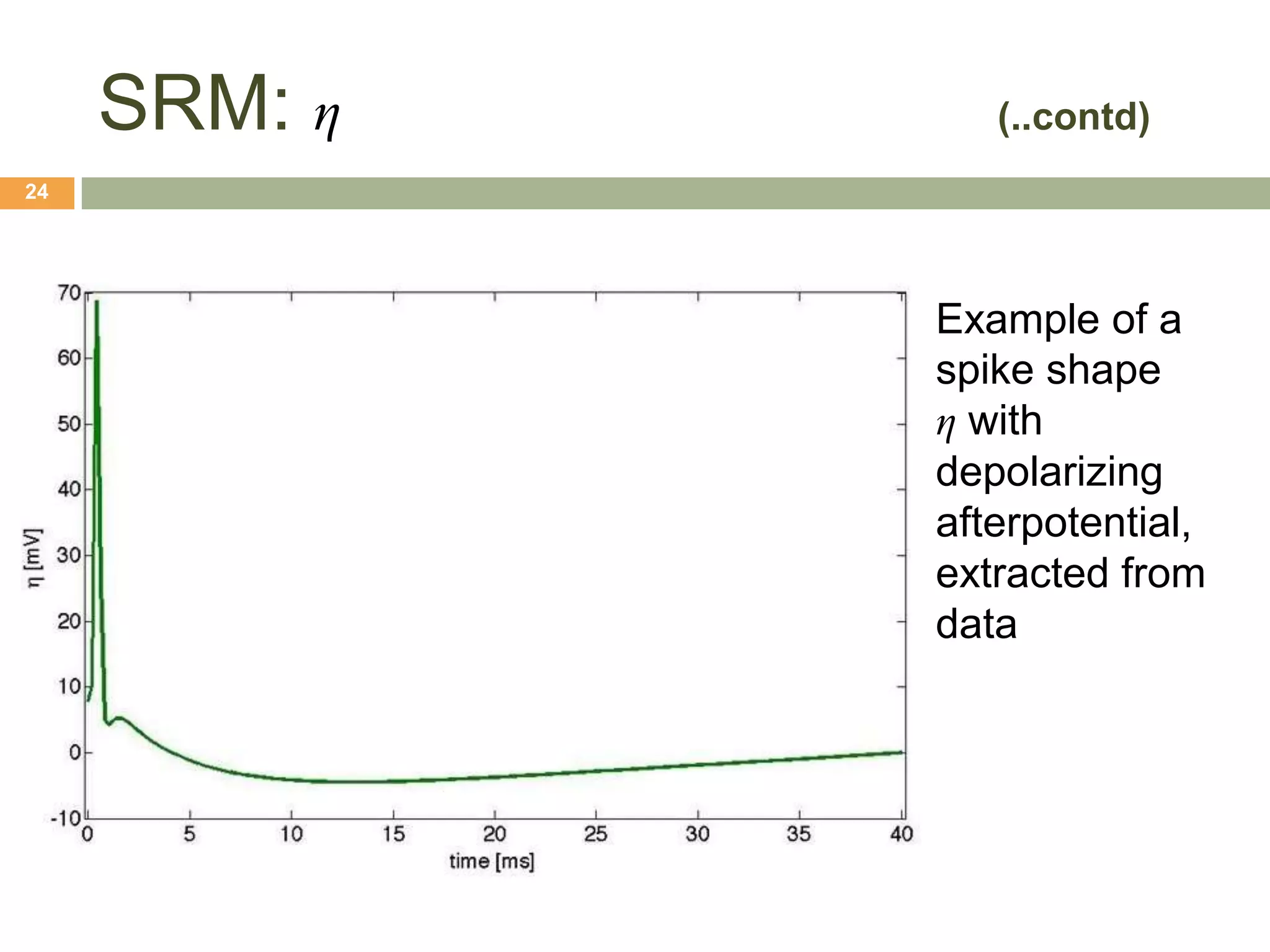
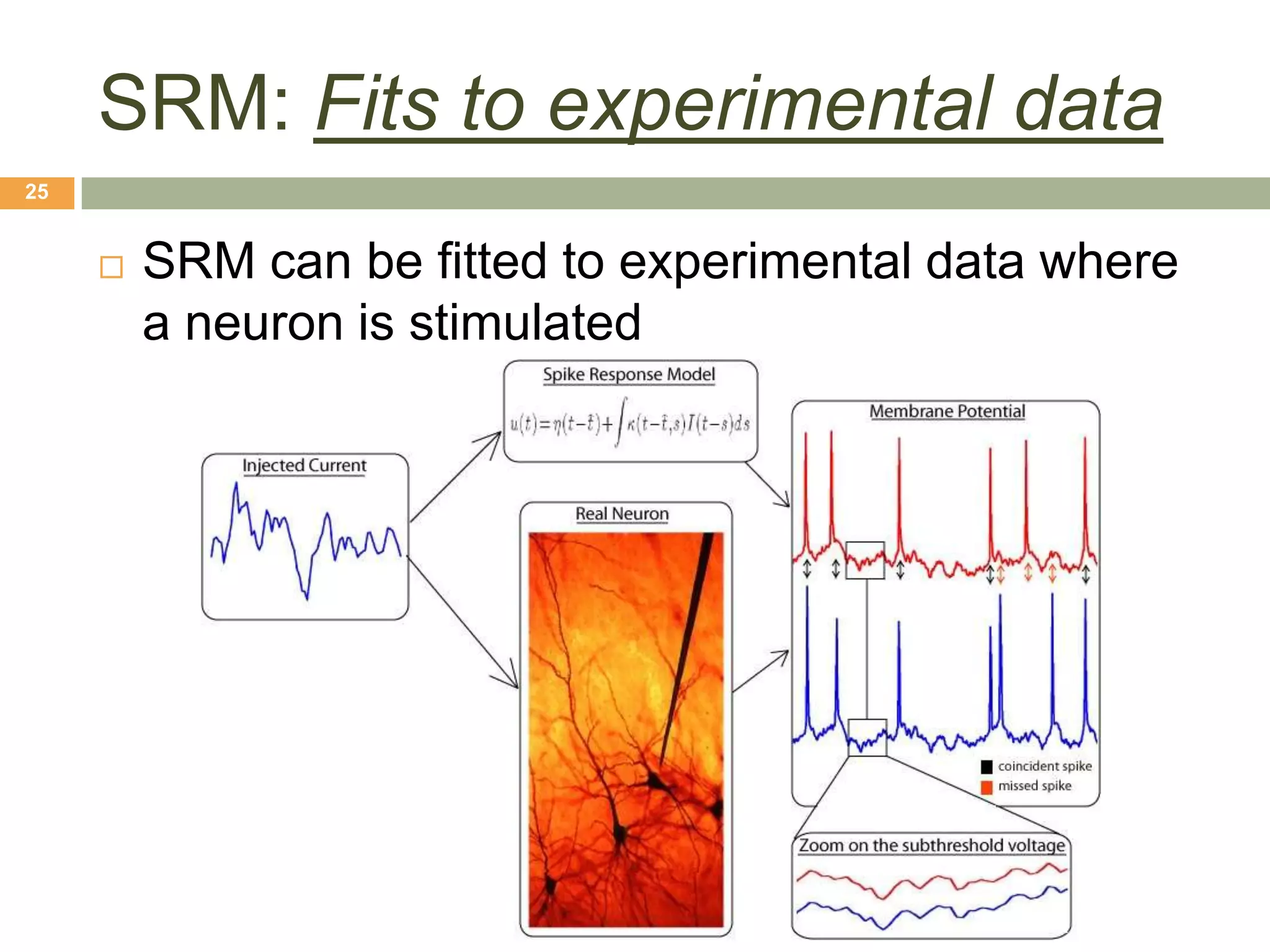
The document outlines various neuron models in neuro-engineering, including the integrate-and-fire, leaky integrate-and-fire, spike-response, and adaptive exponential integrate-and-fire models. It explains the mathematical formulations, characteristics, and applications of these models in simulating real neuronal behavior and action potentials. Additionally, the document discusses limitations and variations of these models, highlighting their relevance in understanding neural dynamics.

1. 1
ZUBIN BHUYAN (CSI 11014)
NAYANTARA KOTOKY(CSI 11025)
NIRUPAM CHOUDHURY(CSI 11033)
Basic Neuro-Engineering

2. Outline
2
 Introduction(neurons and models)
 Integrate and fire based neuron model
 Leaky integrate and fire based neuron model
 Spike-Response Model
 Mathematical Formulation
 Simulating Refractoriness
 Fitting to Experimental Data
 Variations of SRM
 Effects not captured by SRM
 Adaptive Exponential Integrate-and-Fire Model
 Definition
 Adaptation, Delayed spiking, Voltage Response, Initial bursting
 Fitting to real Neurons’ data

3. Review of the neuron
 Action potential- very rapid
change in membrane
potential when a nerve cell
membrane is stimulated.
 Resting potential (typically -
70 mV) to some positive
value (typically about +30
mV).
 Threshold stimulus &
threshold potential(generally
5 - 15 mV less negative than
the resting potential)

4. Neuron model
 Biological neuron model- mathematical
description of the properties of nerve cells.
 Artificial neuron model- aims for computational
effectiveness.

5. Artificial neuron abstraction
Consists of-
 an input with some synaptic
weight vector
 an activation
function or transfer
function inside the neuron
determining output.
 Oj=f( ∑wijei )

6. Biological abstraction
In the case of modelling a biological neuron-
 Physical analogues are used in place of abstractions
such as “weight” and “transfer function’’.
 Ion current through the cell membrane is described by
a physical time-dependent current I(t)
 Insulating cell membrane determines a capacitance
C m.
 A neuron responds to such a signal with a change
in voltage, or an electrical potential energy difference
between the cell and its surroundings, sometimes
resulting in a voltage spike called an action potential.

7. 7
Integrate-and-Fire based Neuron
Model
L. F. Abbott*, 21 May 1999, Lapicque’s introduction of
the integrate-and-fire model neuron (1907)

8. IAF model
 One of the earliest models of a neuron.
 First investigated in 1907 by Louis
Lapicque.
 Lapicque modeled the neuron using an
electric circuit consisting of a parallel capacitor
and resistor.
 When the membrane capacitor was charged to
certain threshold potential
 an action potential would be generated
 the capacitor would discharge

9. Theoretical idea
 In a biologically realistic neural network, it often
takes multiple input signals in order for a neuron to
propagate a signal.
 Multiple input signals goes from one neuron to the
next, increasing the effect of one firing by however
many connection there are(done by adjusting the
weights between each neuron).
 Every neuron has a certain threshold at which it
goes from stable to firing.
 When a cell reaches its threshold and fires, its
signal is passed onto the next neuron, which may
or may not cause it to fire.

10. contd…
 If the neuron does not fire, its potential will be raised
so that if it receives another input signals within a
certain time frame, it will be more likely to fire.
 If the neuron does fire, then the signal will be
propagated onto the next neuron.
 After this, the just-fired neuron goes into a refractory
state, in which it doesn't respond to or propagate
input signals from other neurons.
 This increased potential to fire starts to dampen
soon after the input is received.

11. Mathematical representation
 A neuron is represented in time by
 When an input current is applied, the
membrane voltage increases with time until it
reaches a constant threshold Vth , at which point
a delta function spike occurs and the voltage is reset
to its resting potential, after which the model
continues to run.
 The firing frequency of the model increases linearly
without bound as input current increases.

12. contd…
 By introducing a refractory period tref , we limit the
firing frequency of a neuron by preventing it from
firing during that period.
 Firing frequency as a function of a constant
input current is:
 Shortcoming:
 It implements no time-dependent memory. If the
model receives a below-threshold signal at some
time, it will retain that voltage boost forever until it
fires again.

13. 13 Leaky integrate and fire model
http://lcn.epfl.ch/~gerstner/SPNM/node26.html

14. Description
 In the leaky integrate-and-fire model, the
memory problem is solved by adding a "leak"
term to the membrane potential.
 It reflects the diffusion of ions that occurs
through the membrane when some equilibrium
is not reached in the cell.
(1)
 Rm is the membrane resistance
 threshold Ith = Vth / Rm

15. contd…
 When input current exceeds threshold Ith , it
causes the cell to fire, else it will simply leak
out any change in potential.
 firing frequency is:

16. contd…
 We multiply equation
(1) by R(resistance)
and considering Ω=R
Cm of the “leaky
integrator” to get-

17. 17 Spike-Response Model
Izhikevich, E.M. (2001), Resonate-and-fire neurons,
•
Neural Networks, 14:883-894
Izhikevich E.M. (2003), Simple model of spiking
•
neurons, IEEE Transactions On Neural Networks,
14:1569-1572

18. Spike-response model..
18
 Generalization of the leaky integrate-and-
fire model
 Gives a simple description of action
potential generation in neurons
 Spike response model includes refractoriness

19. SRM: Mathematical Formulation
19
 The membrane potential in the spike response model is
given by
 Here t’ is the firing time of the last spike
 η describes the form of the action potential
 Κ the linear response to an input pulse
 I(t) is a stimulating current
 The next spike occurs if the membrane potential u hits a
threshold Ɵ(t-t’) from below in which case t’ is updated

20. SRM: Mathematical Formulation (..contd)
20
 The threshold Ɵ is not fixed but depends on
the time since the last spike
 threshold is higher immediately after a spike
 then it decays back to its resting value
 The spike shape η is a function of the time
since the last spike
 Itcan describe a depolarizing, hyperpolarizing, or
resonating spike-after potential

21. SRM: Mathematical Formulation (..contd)
21
 The responsiveness Κ to an input pulse
depends on the time since the last spike
 since many ion channels are open
 typically the effective membrane time constant after a
spike is shorter
 The time course of the response Κ can include
 a single exponential
 combinations of exponentials with different time
constants
 or resonating behavior in form of a delayed oscillation
 (This is the case if the standard Hodgkin-Huxley model is
approximated by the Spike Response Model)

22. SRM: Simulating Refractoriness
22
 Refractoriness can be modelled as a
combination of
 increased threshold
 hyperpolarizing afterpotential
 and reduced responsiveness after a spike
 [as observed in real neurons (Badel et al., 2008)]

23. SRM: η (..contd)
23
 Example of a
spike
shape η with
rapid reset,
followed by a
hyperpolarizin
g action
potential,
extracted
from data

24. SRM: η (..contd)
24
 Example of a
spike shape
η with
depolarizing
afterpotential,
extracted from
data

25. SRM: Fits to experimental data
25
 SRM can be fitted to experimental data where
a neuron is stimulated

26. SRM: Fits to experimental data (…contd.)
26
 SRM fits experimental data to a high degree of
accuracy
 Predicts a large fraction of spikes with a
precision of +/-2ms, (Jolivet et al., 2006).

27. Variations of SRM: SRM0
27
 A simplified version of the SRM.
 Does not include a dependence of the response
kernel K upon the time since the last spike
 The threshold can be dynamic as before
 Easier to fit to experimental data than the full
SRM
 since it needs less data (Jolivet et al. 2006)

28. Cumulative Spike Response Model
28
 Refractoriness and adaptation are modeled by
the combined effects of the spike
afterpotentials of several previous spikes
 And not the most recent spike
 The advantage of the cumulative model is that it
accounts for adaptation and bursting

29. SRM with a cumulative dynamic
threshold
29
 Value of the threshold depends on all previous
spikes
 and not only the most recent one
 The threshold Ɵ is calculated as
tk denotes previous moments of spike firing
 Ɵo is the value of the threshold at rest
 v(t-tk) describes the effect of a spike at time tk

30. Noise in the SRM
30
 Noise can be included into the SRM by
replacing the strict threshold criterion,
u(t) = Ɵ, by a stochastic process
 The probability P of firing a spike within a very
short time Δt is
 P = ρ(t) Δt
 where the instantaneous firing rate ρ(t) is a function of
the momentary difference between the membrane
potential u(t) and the threshold Ɵ(t),
 ρ = f(u - Ɵ)

31. Effects not captured by a SRM
31
 Pharmacological blocking of ion channels
 Biophysics of the neuronal membrane is not
described explicitly
 combined effects of several ion channel are
captured
 model cannot make predictions about blocking of
individual ion channels
 Delayed spike initiation due to different
amplitude of the input pulse
 because of the strict threshold criterion
 Dependence of the threshold upon the input

32. Adaptive Exponential Integrate-and-
32
Fire Model
Brette R. and Gerstner W. (2005), Adaptive
Exponential Integrate-and-Fire Model as an
Effective Description of Neuronal Activity, J.
Neurophysiol. 94: 3637 - 3642.

33. AdEx
33
 A spiking neuron model with two equations
 The first equation describes the dynamics of
the membrane potential
 includes an activation term with an exponential
voltage dependence
 Voltage is coupled to a second equation which
describes adaptation
 Both variables are reset if an action potential has
been triggered

34. AdEx: Mathematical Definition
(…contd.)
34
 The model is described by two differential
equations
V is the membrane potential C the membrane capacitance
I the input current EL the leak reversal potential
gL the leak conductance ΔT the slope factor
VT the threshold w the adaptation variable
a is the adaptation coupling parameter τw is the adaptation time constant

35. AdEx (…contd.)
35
 Exponential nonlinearity describes the process of spike
generation and the upswing of the action potential
 a spike is said to occur at the time tf when the
membrane potential V diverges towards infinity
 The downswing of the action potential is a reset
of the voltage to a fixed Vr
at t=tf reset V→Vr
 Also, change the adaption value by b:
w = w +b

36. AdEx: Adaptation
36
 Adaptation and
regular firing of
the AdEx model
in response to a
current step;
voltage (top) and
adaptation
variable (bottom)
[Naud, Marcille, Colpath, Gerstner (2008), Firing patterns in the adaptive exponential integrate-and-fire model]

37. AdEx: Voltage Response
37
 Voltage
response of the
AdEx model to
a series of
regularly spaced
(10 Hz) current
pulse
[Naud, Marcille, Colpath, Gerstner (2008), Firing patterns in the adaptive exponential integrate-and-fire model]

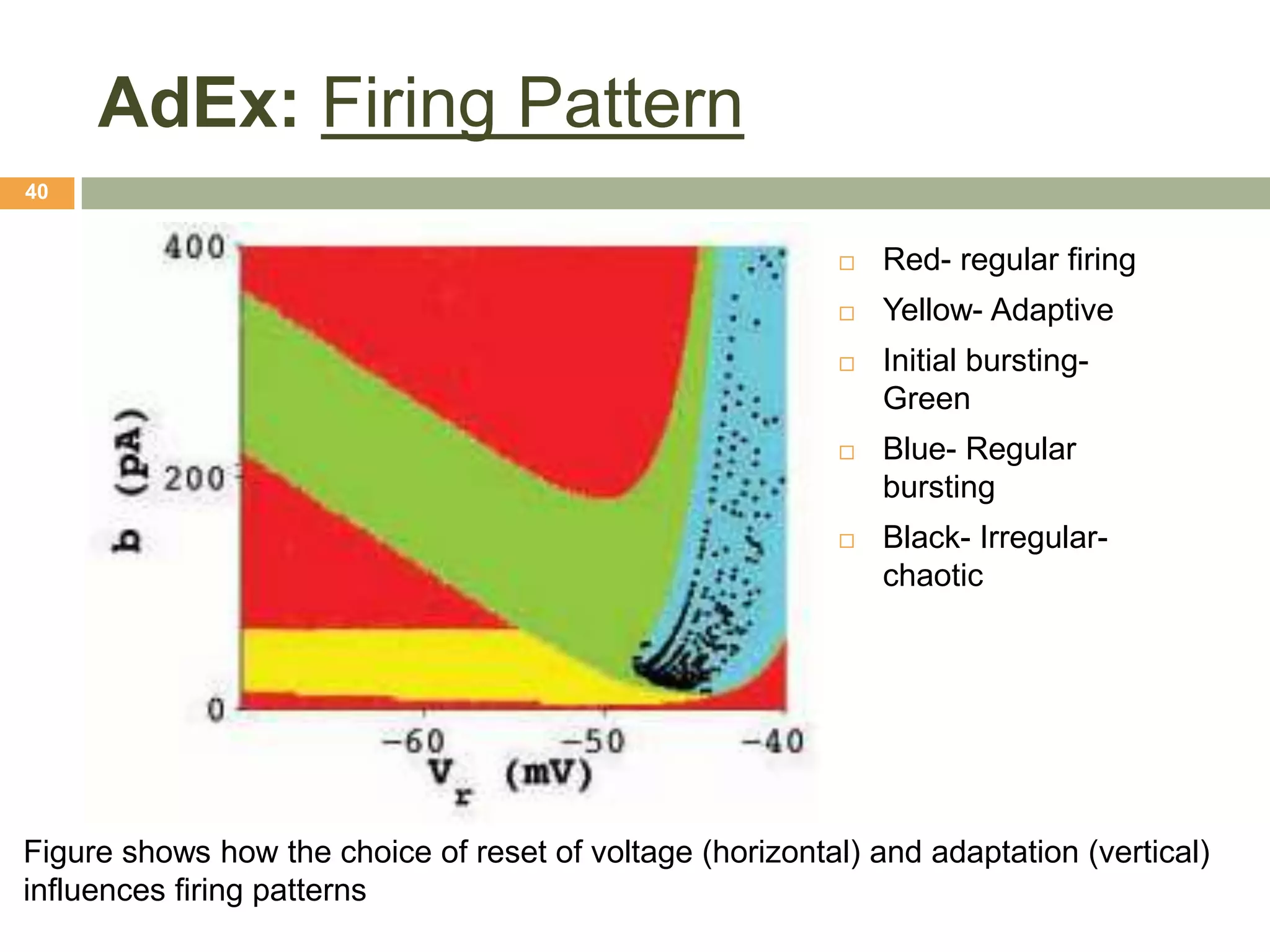
38. AdEx: Initial bursting as response
38
 Voltage (X-axis) and adaptation variable  Voltage as a function of
 Resting potential marked by cross time
 reset values marked by squares
[Naud, Marcille, Colpath, Gerstner (2008), Firing patterns in the adaptive exponential integrate-and-fire model]

39. AdEx: Bursting
39
 Bursting with 3 spikes per burst in the AdEx model
 Bursting occurs when the reset value Vr is high, so that spikes are produced
quickly after reset, until adaptation builds up
[Naud, Marcille, Colpath, Gerstner (2008), Firing patterns in the adaptive exponential integrate-and-fire model]

40. AdEx: Firing Pattern
40
 Red- regular firing
 Yellow- Adaptive
 Initial bursting-
Green
 Blue- Regular
bursting
 Black- Irregular-
chaotic
Figure shows how the choice of reset of voltage (horizontal) and adaptation (vertical)
influences firing patterns

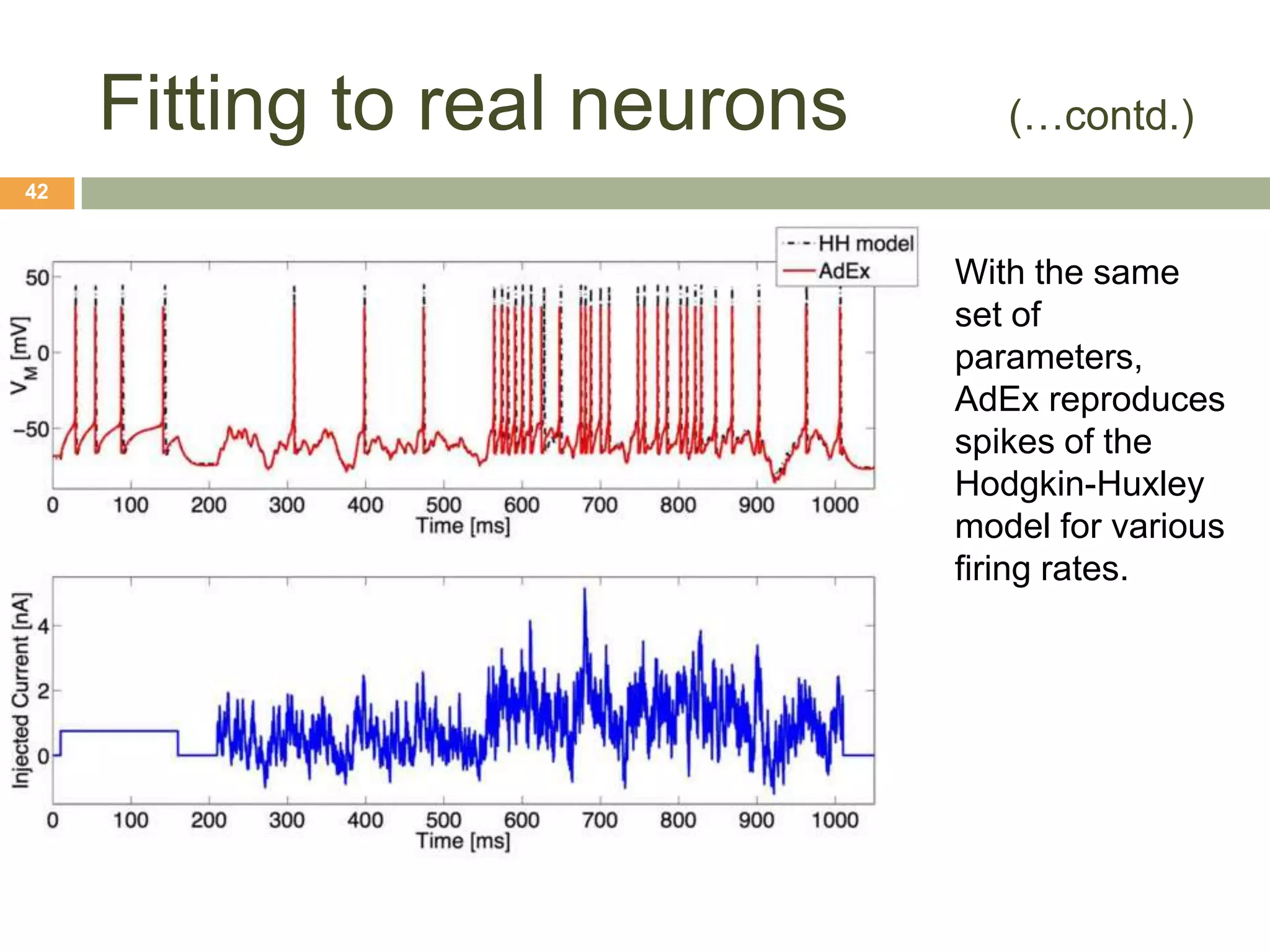
41. Fitting to real Neurons’ data
41
 The parameters of the AdEx model can be fit
to match the response of neurons
 usingsimple electrophysiological protocols
(current pulses, steps and ramps)
 AdEx model can reproduce up to 96% of the
spike times of a regular-spiking Hodgkin–
Huxley-type model
 [Brette and Gerstner, 2005]

42. Fitting to real neurons (…contd.)
42
With the same
set of
parameters,
AdEx reproduces
spikes of the
Hodgkin-Huxley
model for various
firing rates.

43. Some Limitations
43
 Single-compartment model
 But works fine
 Sodium channel activation is instantaneous
 In H-H model activation of the sodium current (via
the m variable) is rapid, but lags the evolution of the
voltage by a short time in the millisecond range
 Downswing of action potential is by resetting to
a fixed value after the spike
 Rapid potassium currents (and also partially by
sodium channel inactivation) is neglected

44. Some Limitations (…contd.)
44
 Refractoriness is only represented by the reset of
voltage and adaptation variables
 in real neurons refractoriness is due to increase in
the firing threshold and conductance after a spike and
a change in the momentary equilibrium potential
 Conductance effects are ignored, because the
adaptation variable enters as a current

45. REFERENCES
45
1. Abbott, L.F. (1999). "Lapique's introduction of the integrate-and-fire model neuron
(1907)“
2. Izhikevich, E.M. (2001), Resonate-and-fire neurons, Neural Networks, 14:883-894
3. Izhikevich E.M. (2003), Simple model of spiking neurons, IEEE Transactions On
Neural Networks, 14:1569-1572
4. Brette R. and Gerstner W. (2005), Adaptive Exponential Integrate-and-Fire Model
as an Effective Description of Neuronal Activity, J. Neurophysiol. 94: 3637 - 3642.
5. Naud, Marcille, Colpath, Gerstner (2008), Firing patterns in the adaptive
exponential integrate-and-fire model, Biological Cybernetics, DOI
10.1007/s00422-008-0264-7
6. Benda J, Herz A.V.M. (2003), A universal model for spike-frequency adaptation.
Neural Comput. 15:2523-2564.
7. http://www.scholarpedia.org/Spike-response_model (doi:10.4249/scholarpedia.1343)
8. Koch, Christof; Idan Segev (1998). Methods in Neuronal Modeling (2 ed.).
Cambridge, MA: Massachusetts Institute of Technology. ISBN 0-262-11231-0
9. http://lcn.epfl.ch/~gerstner/SPNM/node26.html

46. Thank You!
46

47. 47

48. AdEx: Delayed spiking
48
 Delayed spiking as
response of the AdEx
model to a current step
Voltage as a function of time
[Naud, Marcille, Colpath, Gerstner (2008), Firing patterns in the adaptive exponential integrate-and-fire model]