The document is a PowerPoint presentation analyzing a simple maglev system using Simulink. It includes: - An introduction to maglev systems and their applications. - Circuit diagrams and explanations of the position sensor, electromagnet actuator, and other system components. - Derivations of the system's mathematical model and equations in state space form for both nonlinear and linear controller approaches. 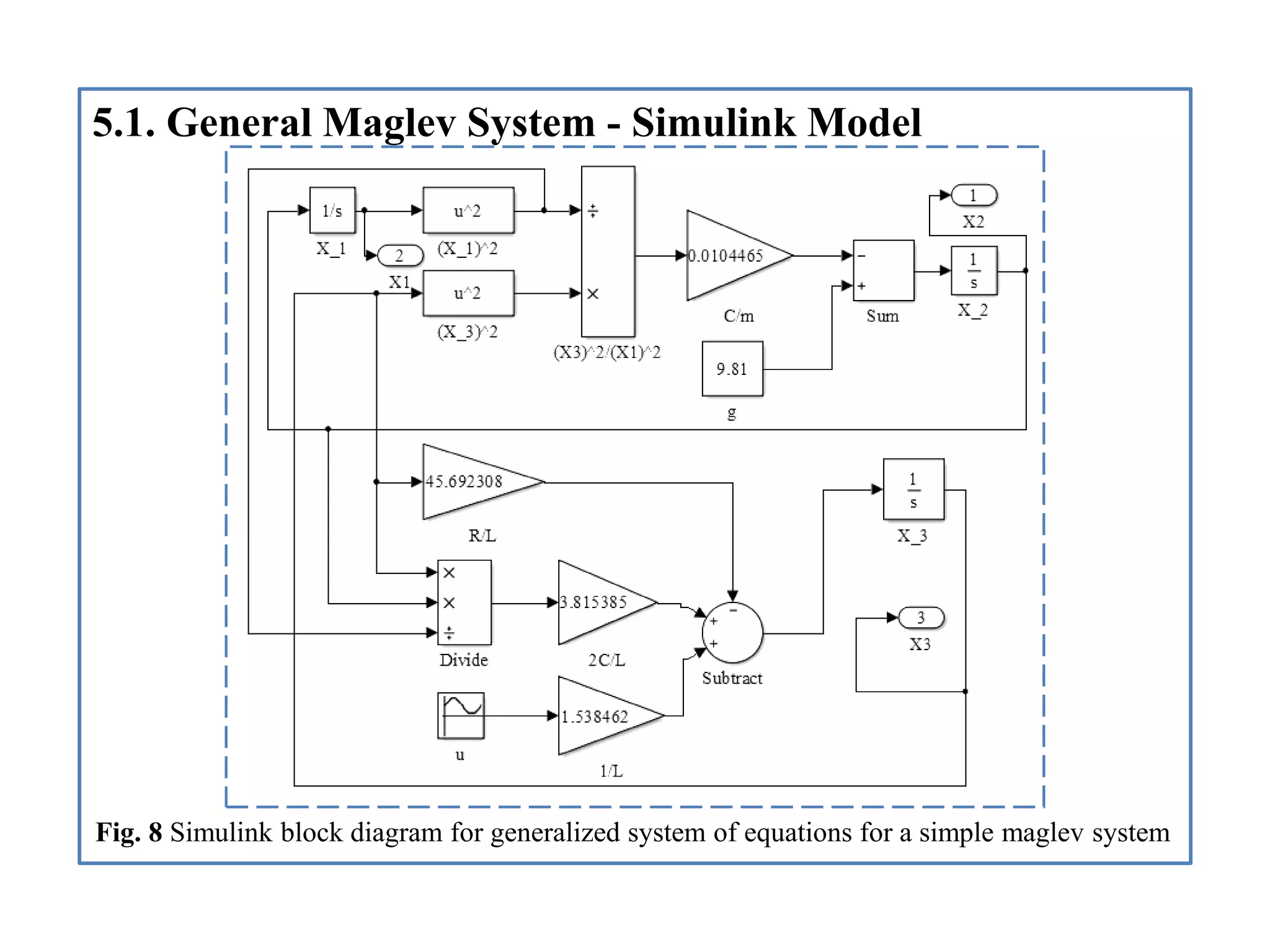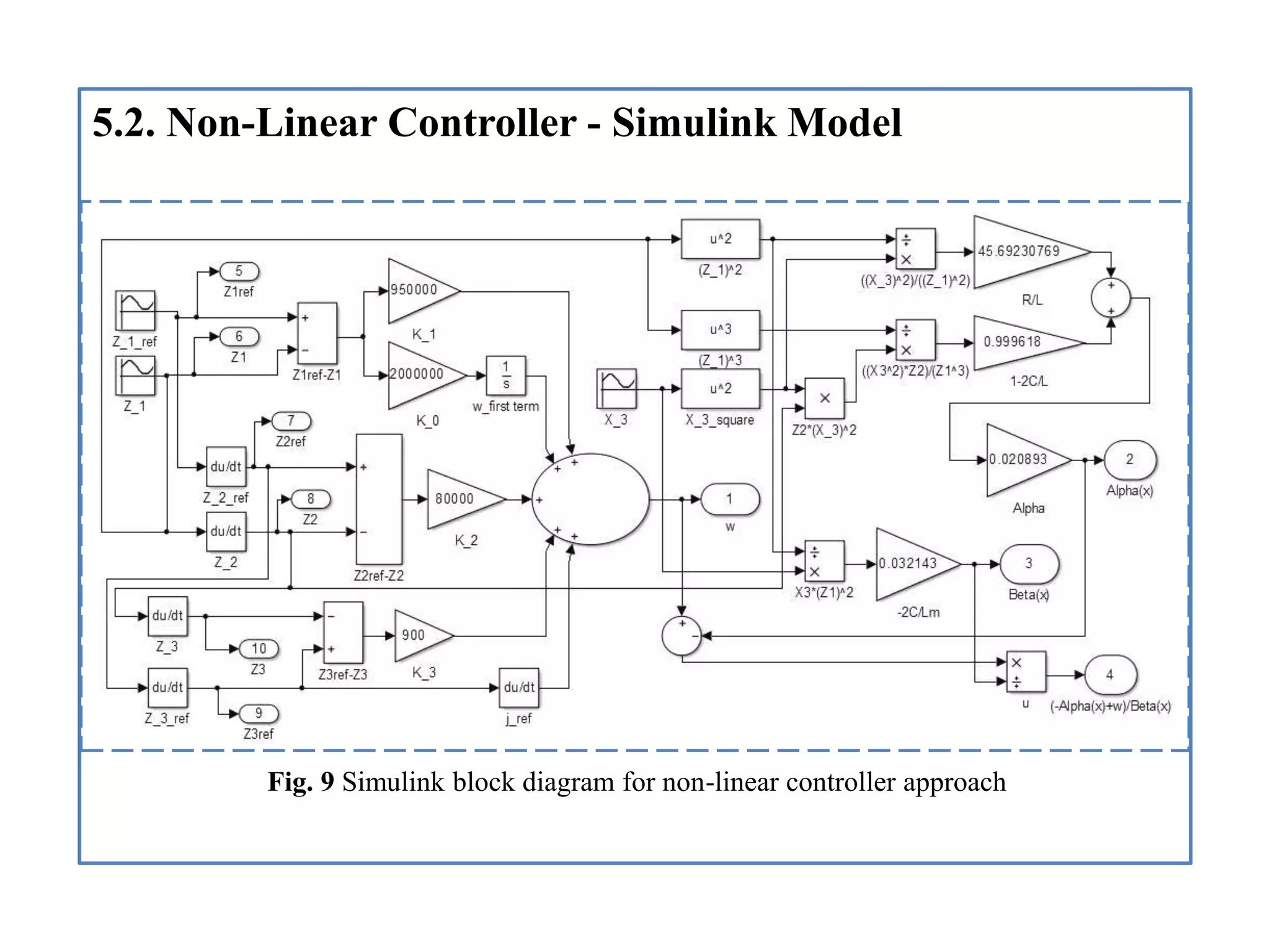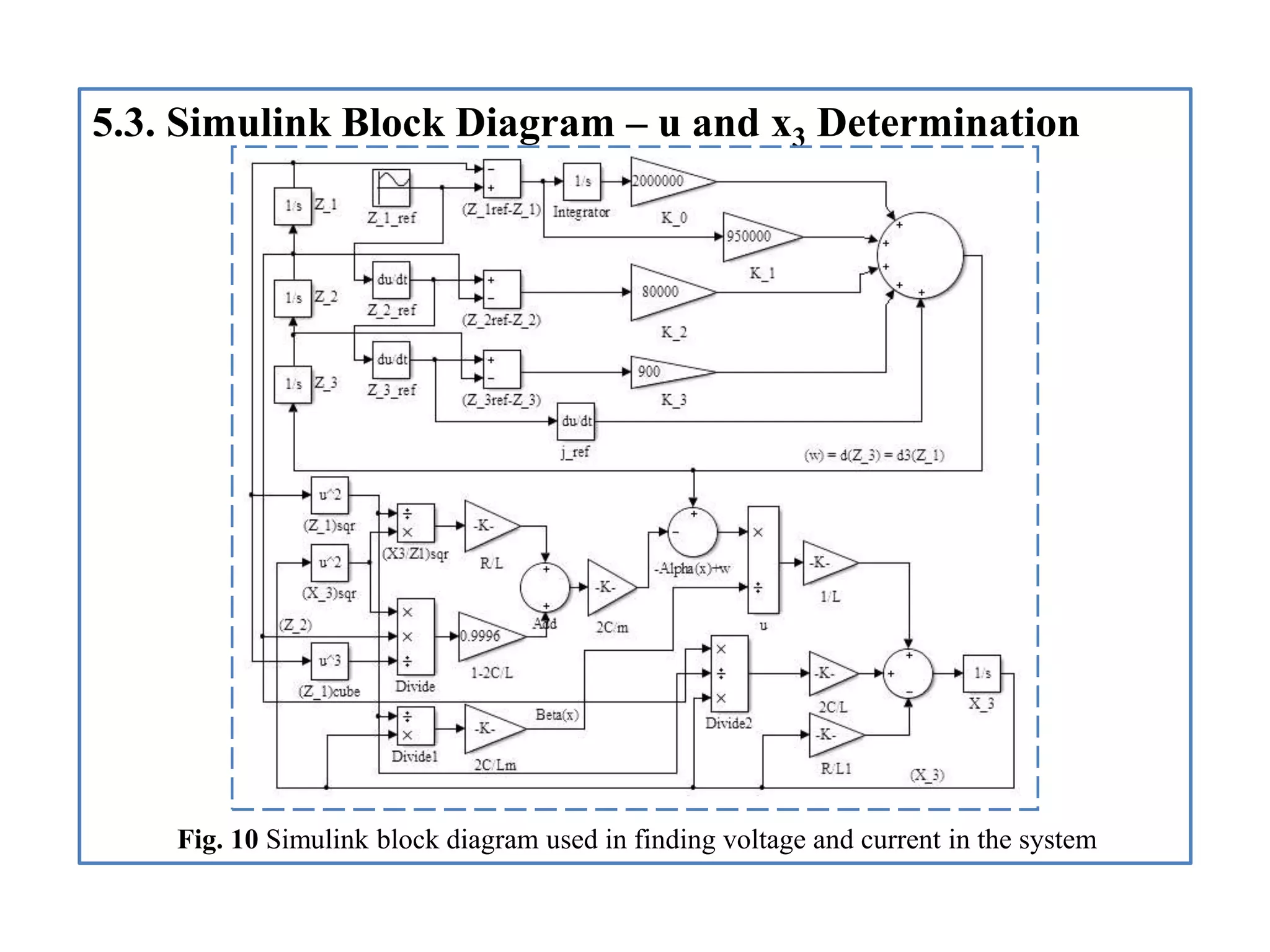- Descriptions of the Simulink models created to simulate the system, including blocks for the generalized system, nonlinear controller, and determining voltage and current. 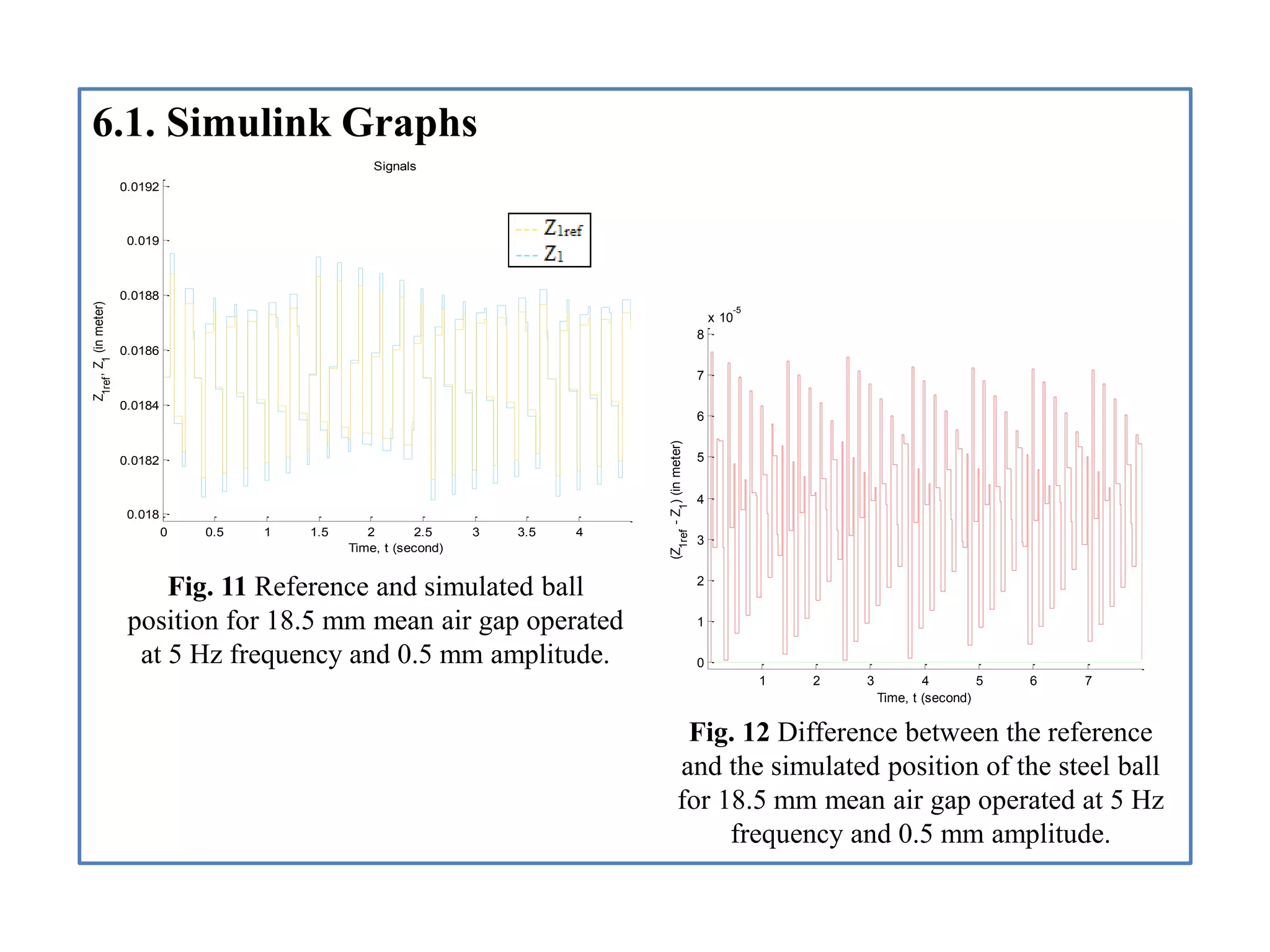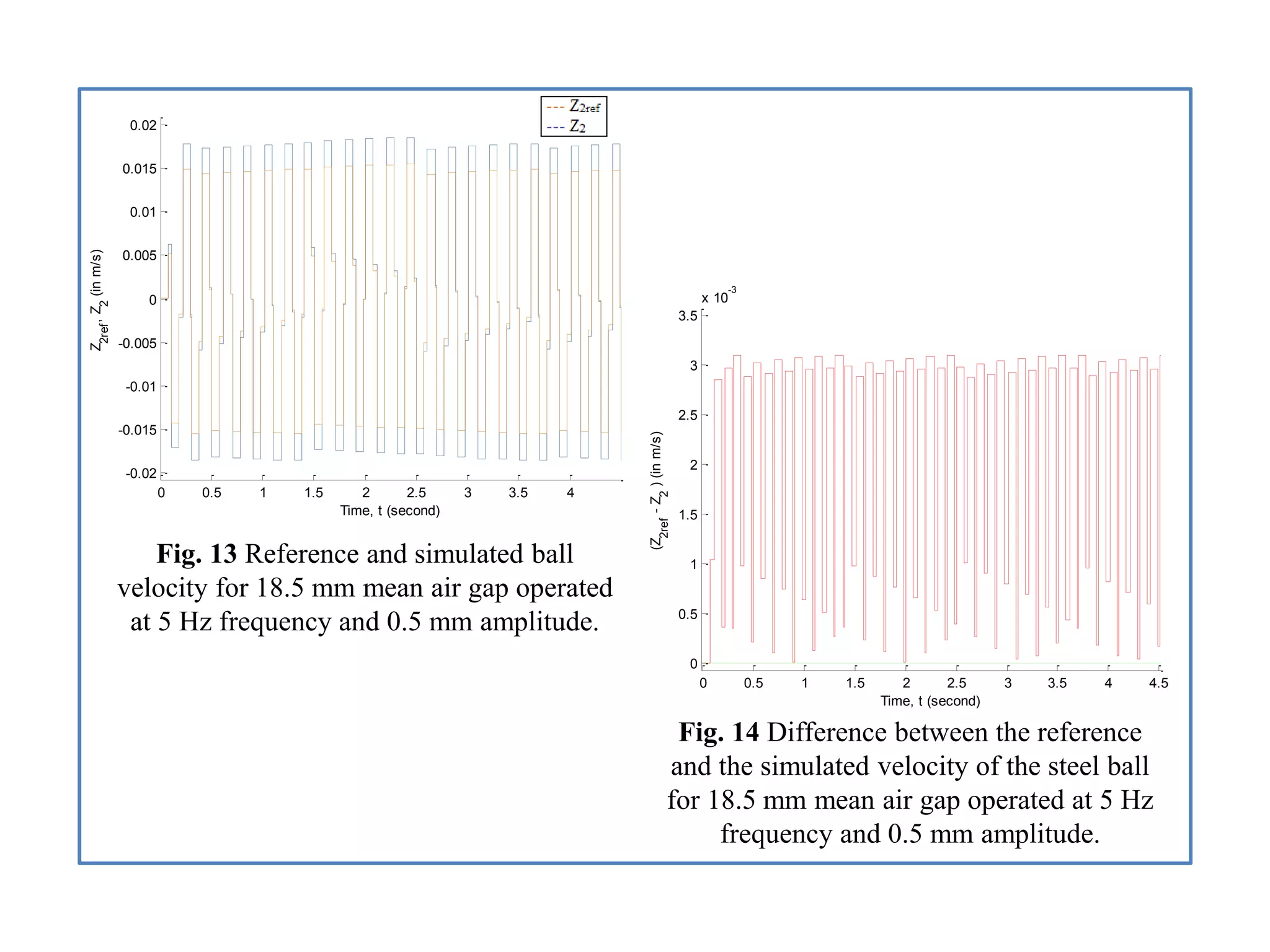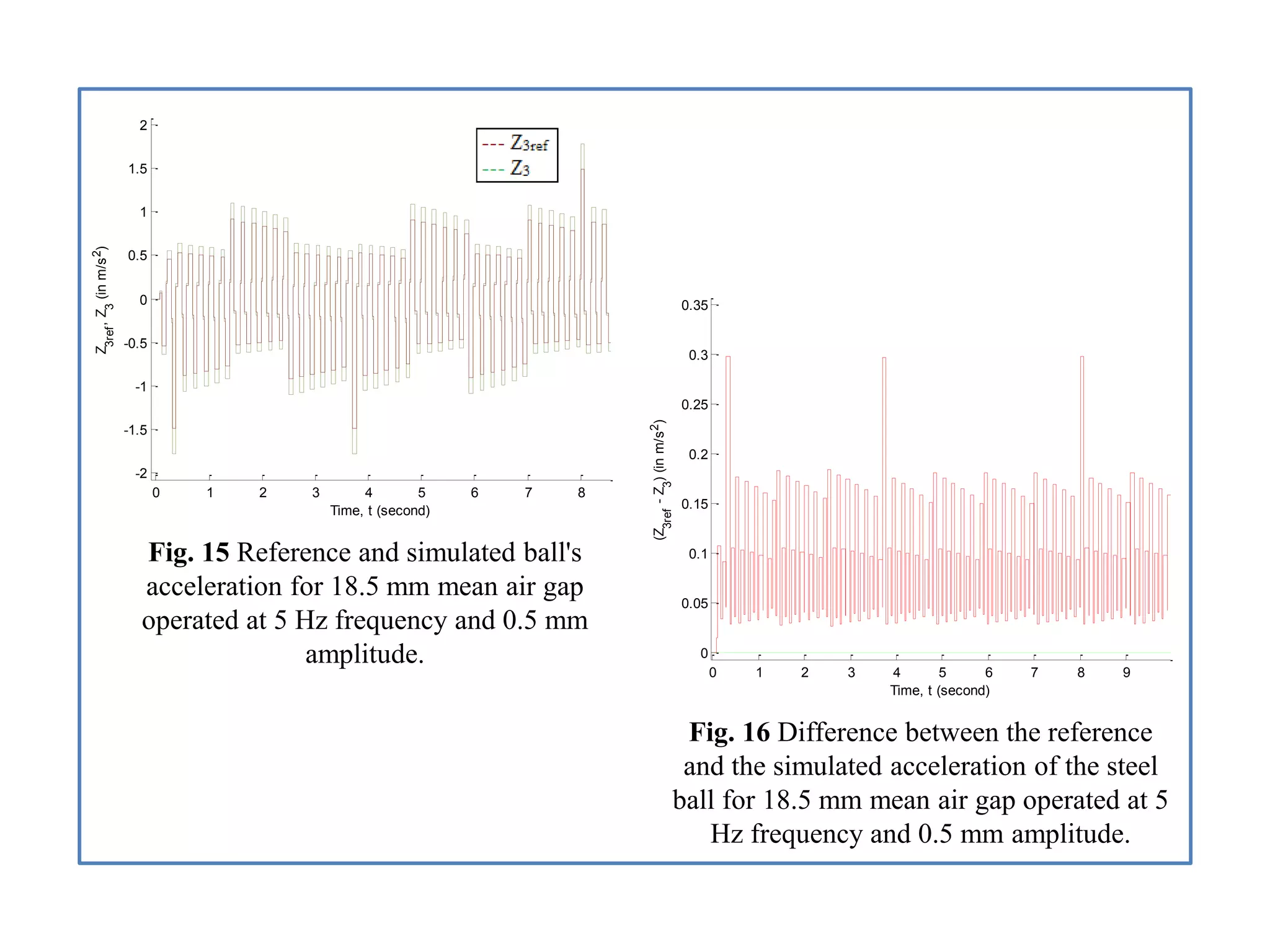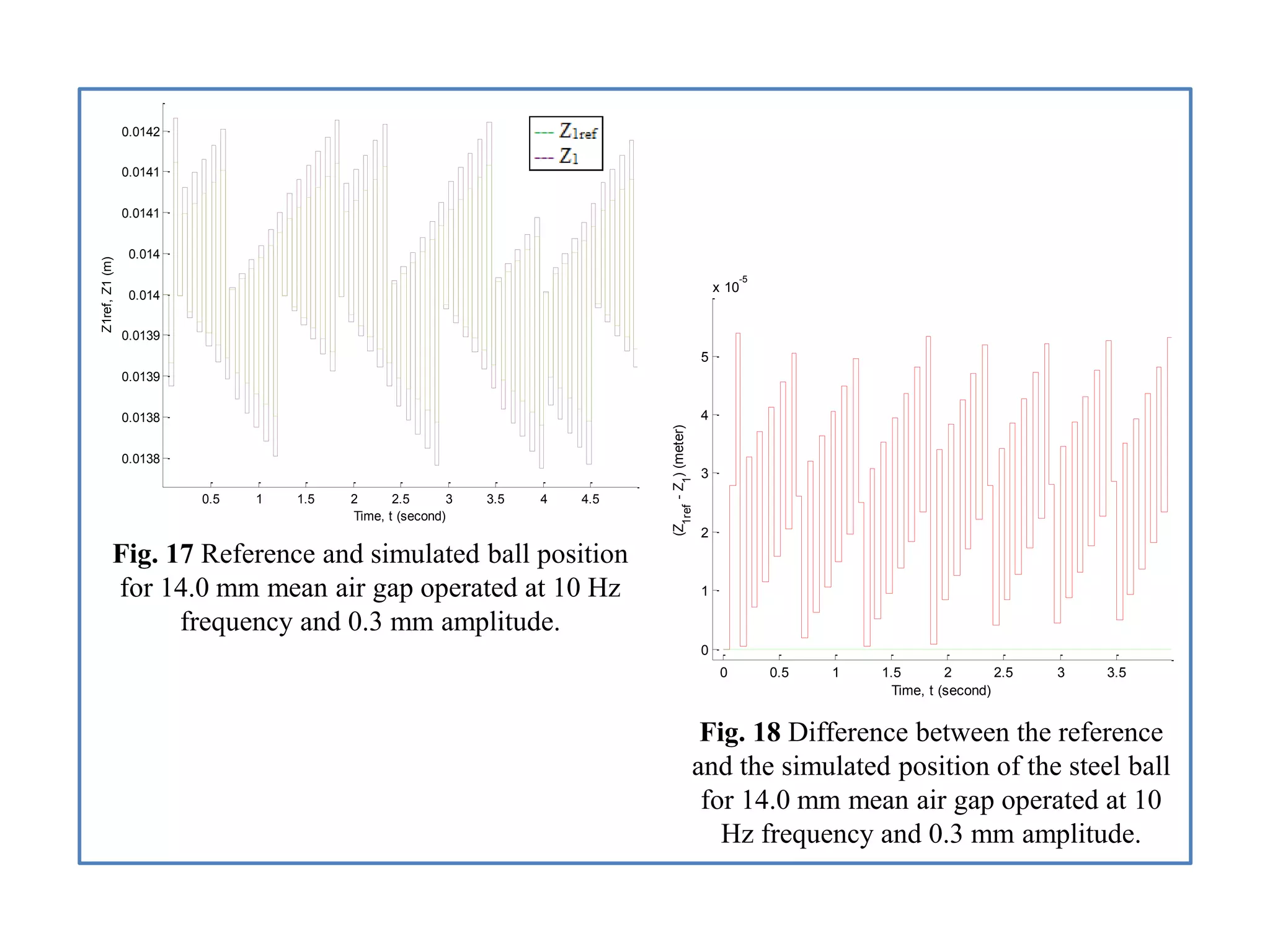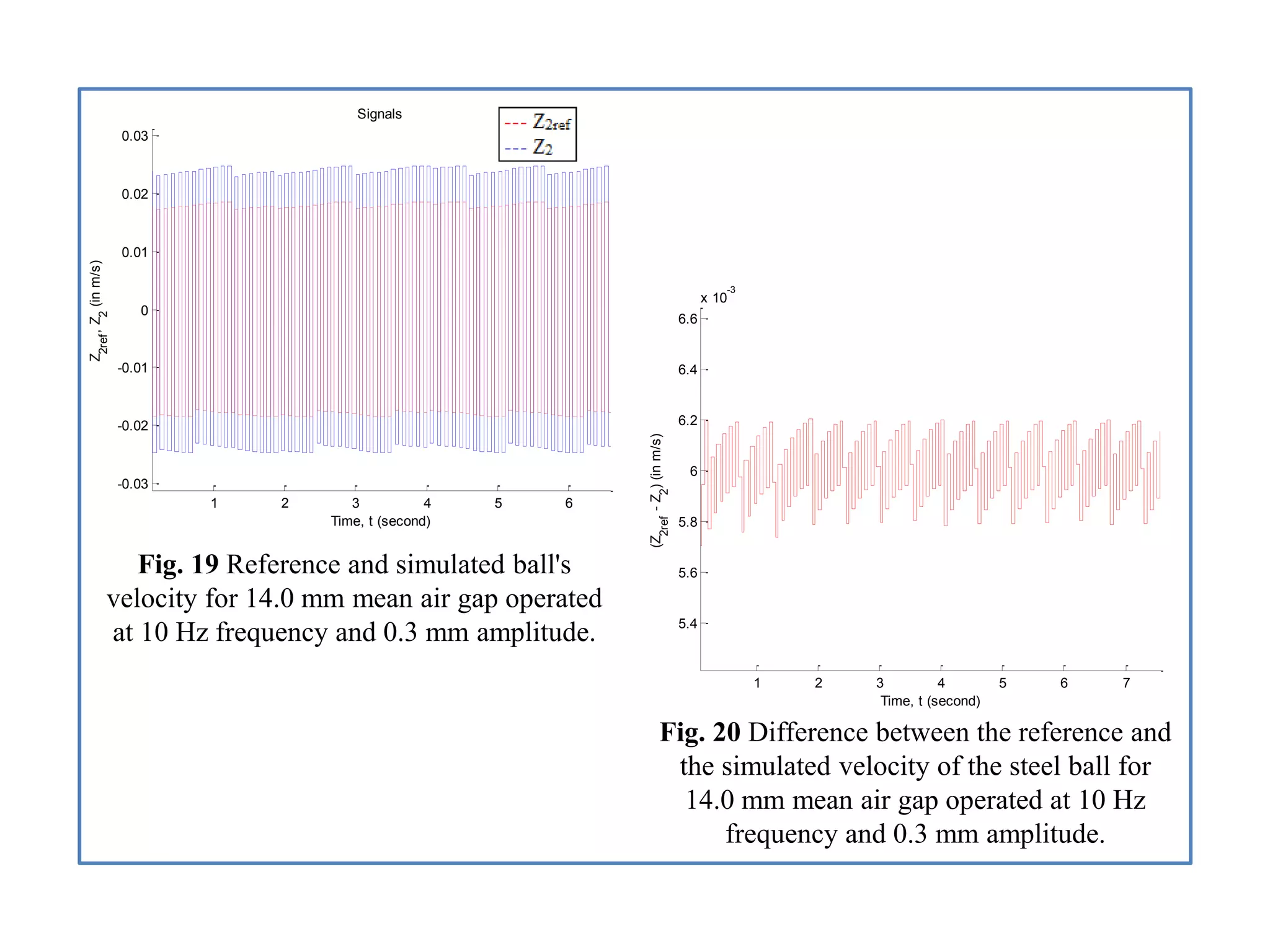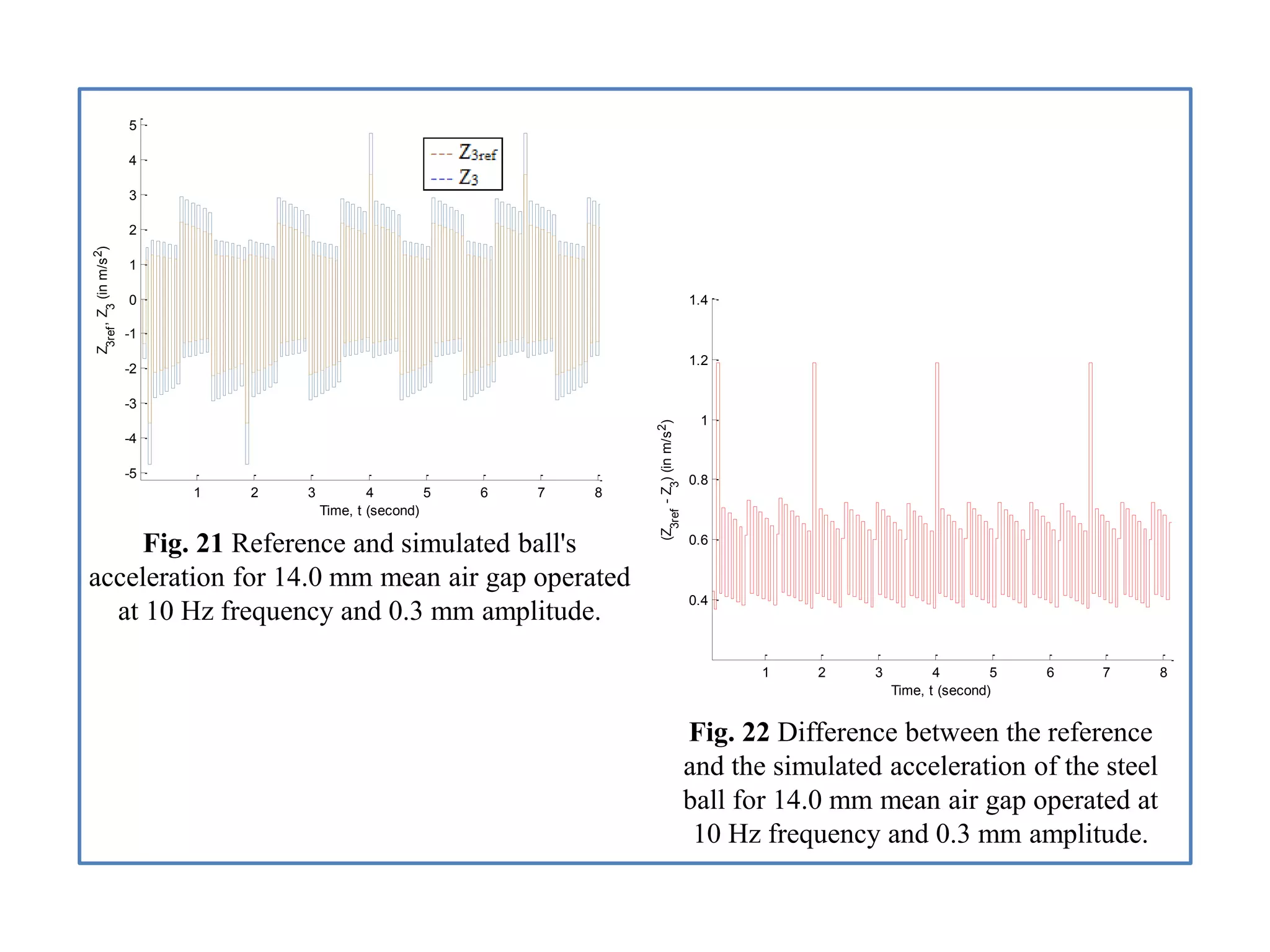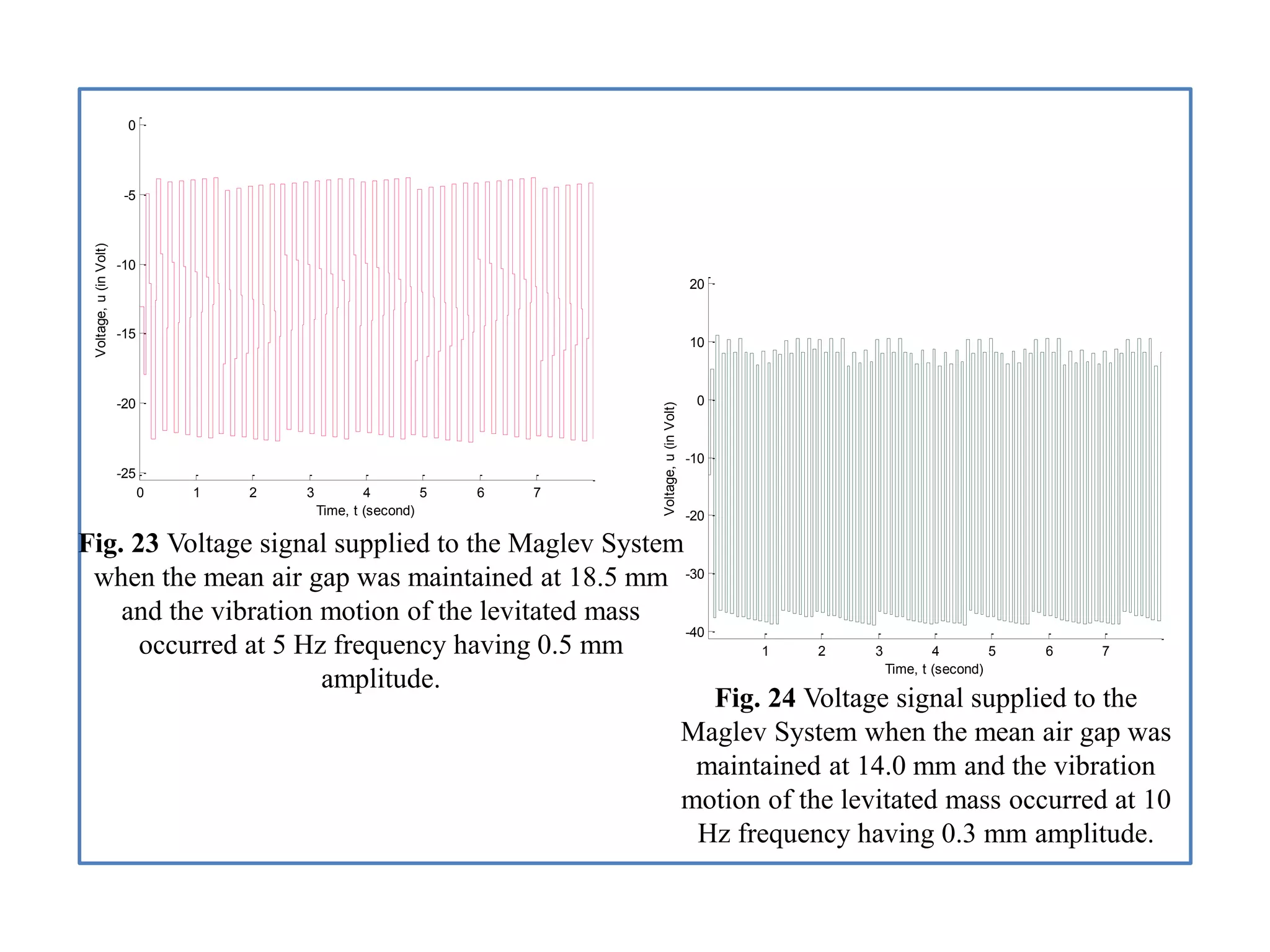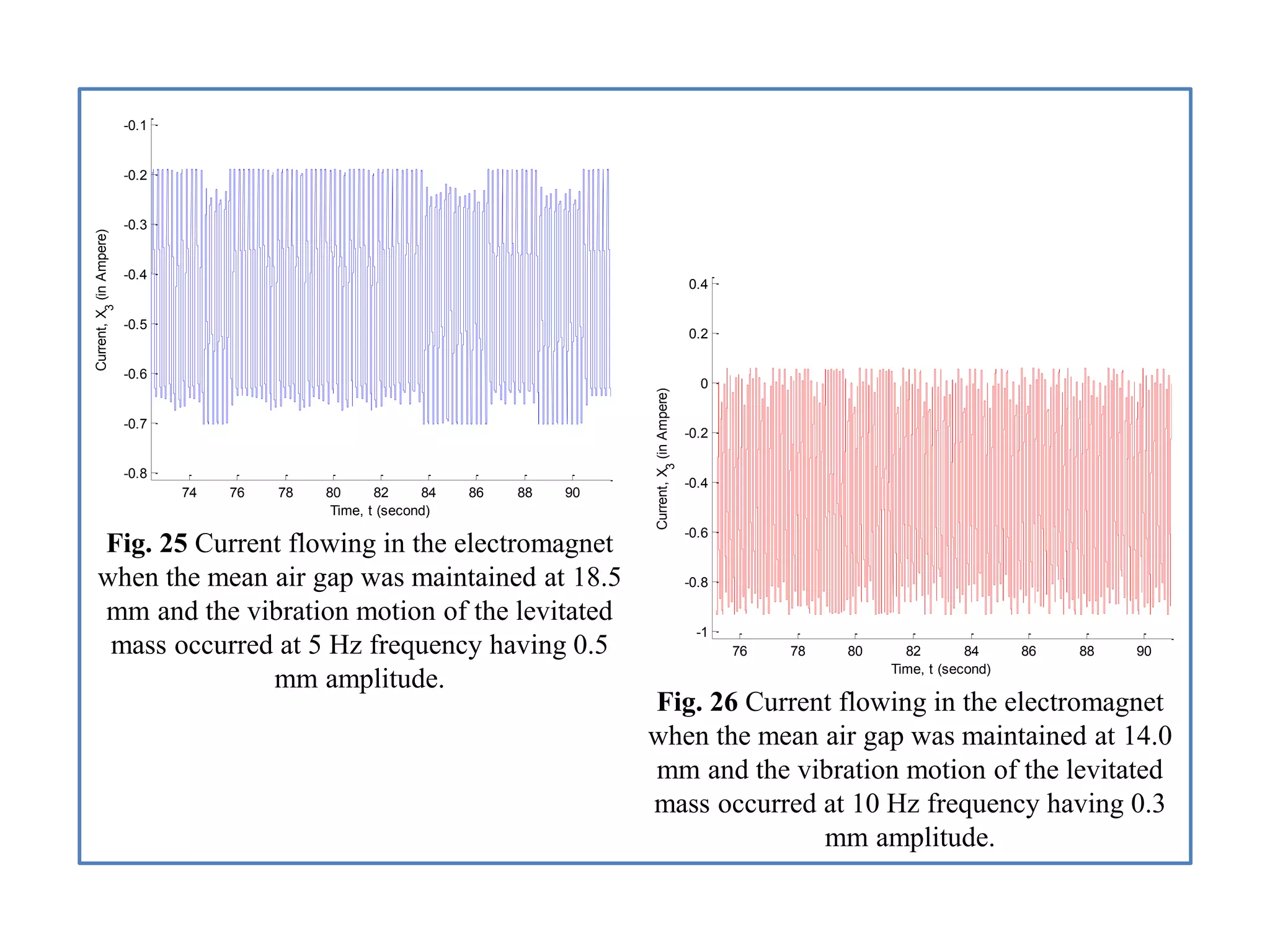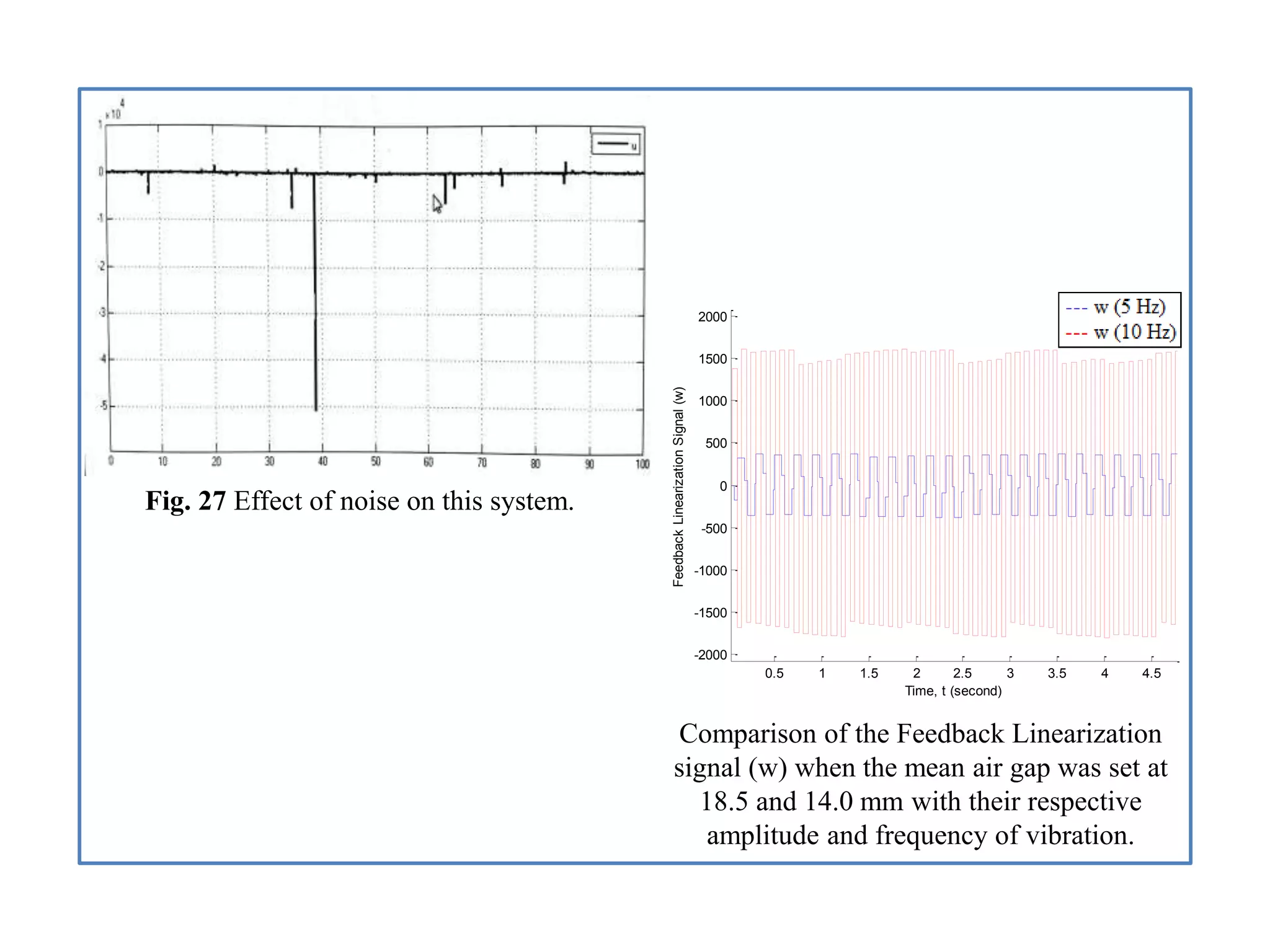- Analysis of simulation results for two air gap scenarios, comparing graphs of position, velocity, acceleration, and other signals between the scenarios.

1. A PowerPoint Presentation
On the Topic
‘Analysis of Simple MagLev System using Simulink’
Made and Submitted By
Arslan Guzel, 13MEB451
Mohd. Adnan, 13MEB417
Manish Dixit, 13MEB323
Under the supervision of
Dr. Mohd. Yaqoob Yasin
Department of Mechanical Engineering
Zakir Hussain College of Engineering Technology
Aligarh Muslim University, Aligarh
2016-17

2. Abstract
A simple Maglev system has three basic and important variables, which are the
fundamentals of even the most of the complex Maglev system, and these are – air
gap, velocity of ball, and current flowing in the electromagnet. The important
circuitry elements are satisfactorily explained for an understanding basis. sensor.
Further, the non-idealities for the electromagnet force constant, C is mentioned and
variation with the ideal values is compared theoretically and explained why we have
considered the theoretical value. Latter, the Maglev system is algebraically
formulated in general state-space form, and then by considering non-linear and linear
control theroy approach separately. The results are presented for two values of air
gaps with correspondingly different amplitude and frequency of vibration. The trends
followed by the kineamatic variables are sufficiemntly explained. The comparison
for current, feedback signal, and voltage supplied is done between the two cases. The
general understanding, concepts, and a detailed overview is given along with
practical implications to enable the reader to carry out further analysis on the
MagLev systems.

3. Content
1. Introduction
2. Circuit Elements
2.1. Actuator
2.2. Linear Amplifier
2.3. Position Sensor-Light Source, and Light Sensor
3. Magnetic Force Constant
3.1. Effect of Permeability, Hysteresis, Saturation on ‘C’
4. Problem Formulation
4.1. General State-Space Form
4.2. Non-Linear Controller Approach
4.3. Linear Controller Approach
5. MATLAB Application
5.1. General Maglev System - Simulink Model
5.2. Non-Linear Controller - Simulink Model
5.3. Simulink Block Diagram - Voltage and Current Determination
6. Data Analysis and Results
6.1. Simulink Graphs
6.2. Results and Discussion
6.3. Conclusions
References

4. 1. Introduction
 Maglev = Magnetic + Levitation.
 Magnetic Force exists in Nature – Earth – North, and South Poles.
 Has led to amazing phenomenon(s) like Aurora Borealis and Aurora Australis[1].
 Maglev trains –train floats over guide rails – eliminating friction - reach speeds up
to 350 mph.
 Magnetic bearings - no contact between moving surfaces – use of lubricant is
vanquished – virtually infinite life.
 Also has ability to withstand high and very low temperature, and vacuum.
 Some other applications - magnetic levitation of wind tunnel models, vibration
isolation of sensitive machinery, levitation of molten metal in induction furnaces,
high vacuum pumps, milling spindles, grinding spindles, gyroscope for space and the
levitation of metal slabs during manufacture.
 This paper is a presentation on a single axis electromagnetic suspension system.
 Maglev Systems - non-linear dynamics – unstable in open-loop control.
 Every Maglev system consists of three basic components - position sensor,
actuator,, controller and amplifier.

5. 2. Circuit Elements
 A steel ball is suspended between the light source and detector.
 The photodiode array produces a current proportional to the amount of light
detected, which in turn depends upon the position of the steel ball.
 The transresistance amplifier converts the photodiode current into a voltage
representative of position, which is processed by the computer. After completion of
this process, the amplifier receives the voltage signal from the computer and in
response changes the amount of current flowing into the coil correspondingly.
 The position sensor uses an array of bright light emitting electrical/electronic
equipment as a light source and a photosensitive screen as a light detector.
Fig. 1 Schematic representation of Maglev system

6. 2.1. Actuator
 Actuator = Electromagnet coupled with Controller.
 Electromagnet is a core, made up of electrically conducting material (generally
soft iron), wounded by insulated wires in a proper fashion around it. The more the
number of turns the more is the electromagnetic force generated.
 Controller is an electrical equipment which must have an amplifier preceding it.
2.2. Linear Amplifier
 Amplifier chosen according to it’s slew rate.
 Slew rate – Function(Type of input, type of output and range of operation).
 Slew rate defines the ability to change the current drawn into the circuit.
 If air gap  0, This calls for the need of maximum negative slew rate amplifier.

7. 2.3. Position Sensor
 Light detected by position sensor α (air gap).
 Position Sensor calibrated initially (as per experiment need).
2.3.1. Light Source
 Light source is vertical array of anything that emits light but should have the
characteristics mentioned as follows:
 high output intensity ( in lumen )
 low power consumption
 effectively operate on low current value
 least interference with ambient light
Therefore, LED light are preferable over incandescent light.
2.3.2. Light Sensor
 Light sensor is a photosensitive diode array that senses light falling on it and
responds by producing an output voltage corresponding to the intensity of light
received.

8. Fig. 2 A Light Source
Fig. 3 Circuit diagram of a 5 element Light Source

9. 3. Magnetic Force Constant
 Denoted by ‘C’, and has unit Nm2/A2 (in SI).
 For an ideal case the force produced by the electromagnet is written in the
following form,
 The above equation shows that the air gap must never be zero, and if so the force
exerted will be infinite which is impractical.
 In our case the air gap variable is taken to be greater than 10.0 mm. Thus, this
non-ideality has no effect.
Permeability is the ability of a magnetizable substance to modify the magnetic
flux in the region occupied by it in a magnetic field. Ideally it is assumed that
everywhere there is infinite permeability except in the air gap. If x  0, this implies
the flux should reach ∞.
 The above two non-idealities can be corrected by replacing ‘x’ by (x+x0).
 Hysteresis - A phenomenon of decreased value of magnetic field density due to
material properties happening during a cyclic reversal of magnetic intensity supplied
to the electromagnetic material. Or the ferromagnetic material tends to stay
magnetized even after the magnetic intensity is turned to zero.

10.  Remedy – use softer Iron core.
 Hysteresis also states that the magnetic flux is dependent on both the current
flowing into the coil and prior history of magnetization.
Thus, arithmetic mean of flux is taken which can be determined as shown in the
figure 5.
Fig. 4 Hysteresis Curve
Fig. 5 Arithmetic mean of force curve versus time

11.  Saturation is a phenomenon, which causes slower increase in magnetic field
density relative to prior rate of increase while increasing the magnetic field intensity.
 Occurs in all iron core magnets.
 When a small amount of force is applied, the domains in the electromagnetic
material align in large numbers easily and produce high magnetic field density.
However, as the magnetic field intensity (force) is increased less number of domains
are left to be aligned. At this point beyond, after certain magnitude of force has been
supplied further increasing the force produces no more magnetic field density. This
phenomenon is termed as 'saturation'.
 In figure 5 the curve segment corresponding to the highest values of current
represents saturation.

12. 4. Problem Formulation
 Enables to understand the system with or without any assumptions as required.
 Algebraic formulation – mathematical representation – dependency of results with
respect to variables – Neglecting of terms and defining additional or new approach
becomes easier.
 Thus, algebraic problem formulation eases the understanding, and in laboratory
conditions give approximate results, which are quite sufficient to solve errors
occurring in real life situations.
 Drawback – All real life situations can not be modelled algebraically perfectly
without taking impractical assumptions into account.

13. Fig. 6 Forces acting on ball: Schematic representation

14. Fig. 7 Circuit diagram of a simple Maglev system

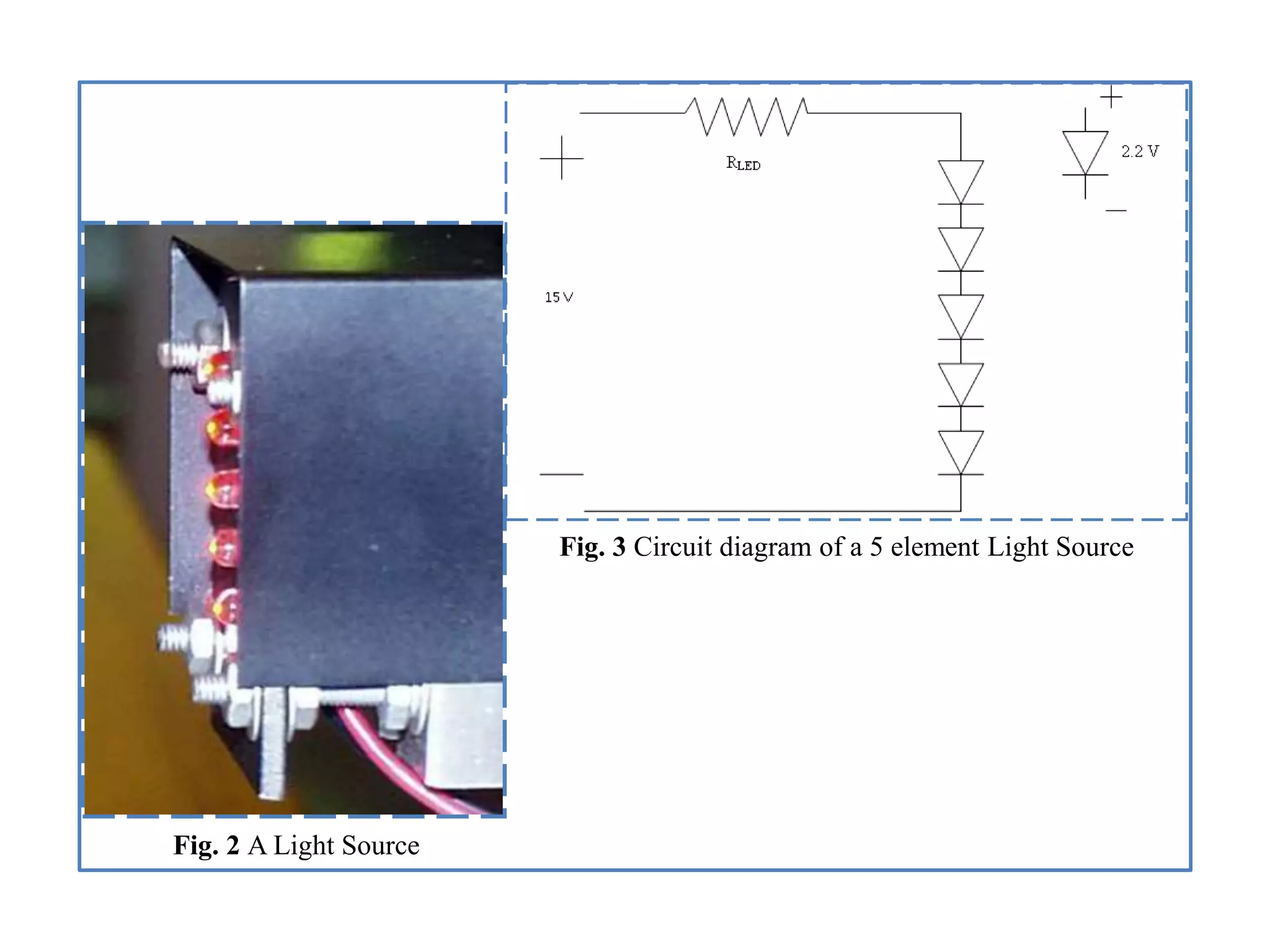
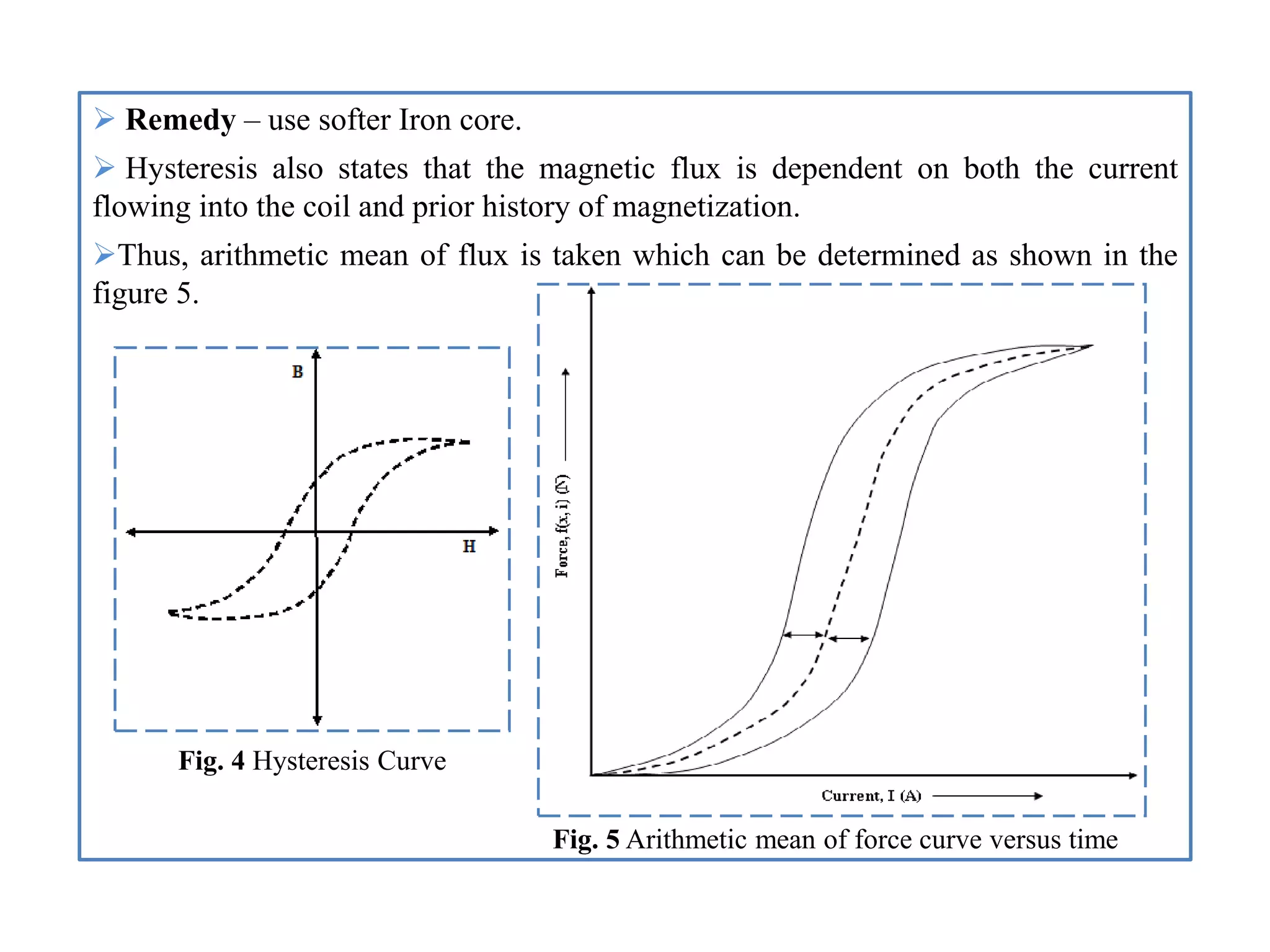
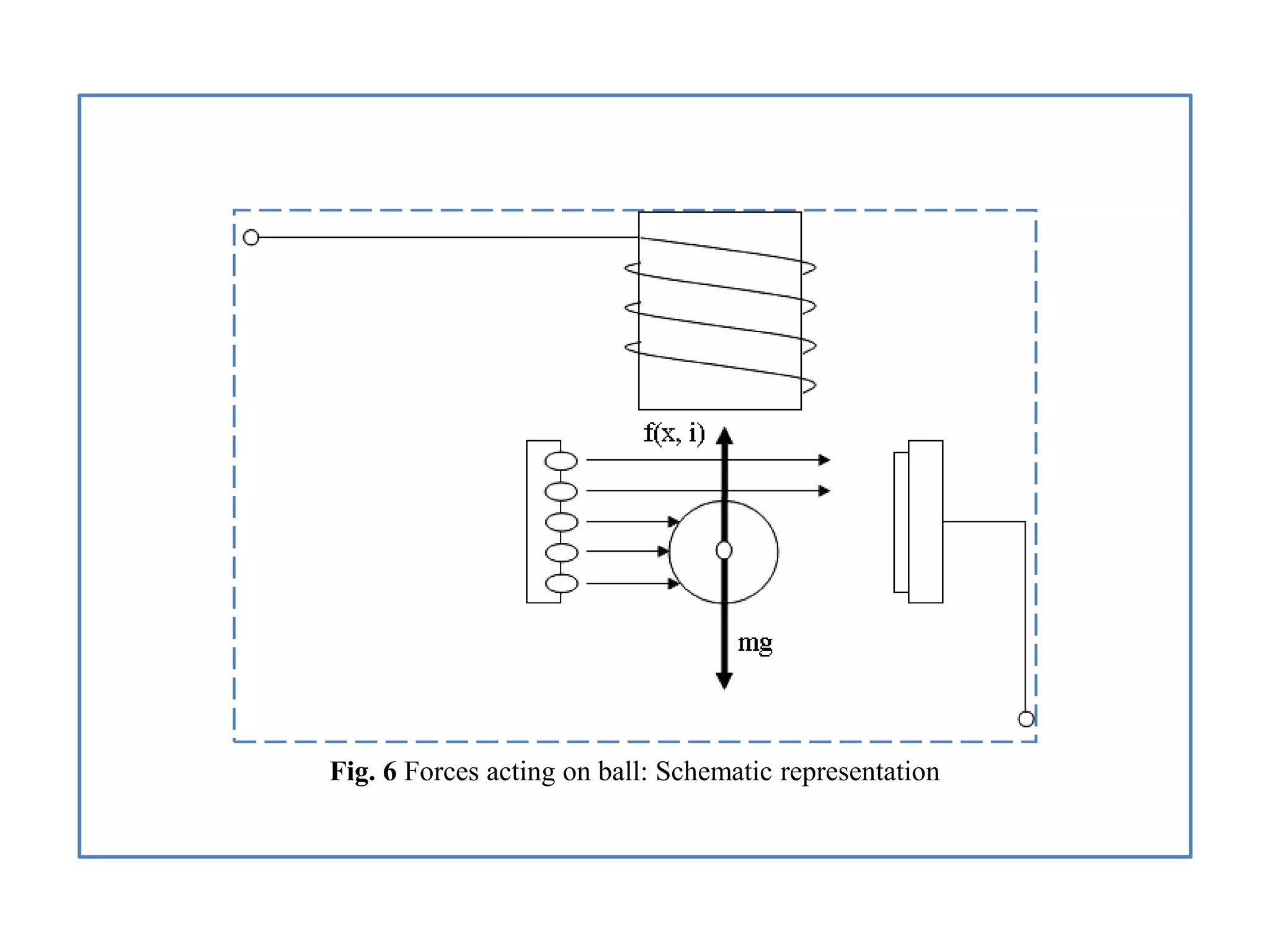
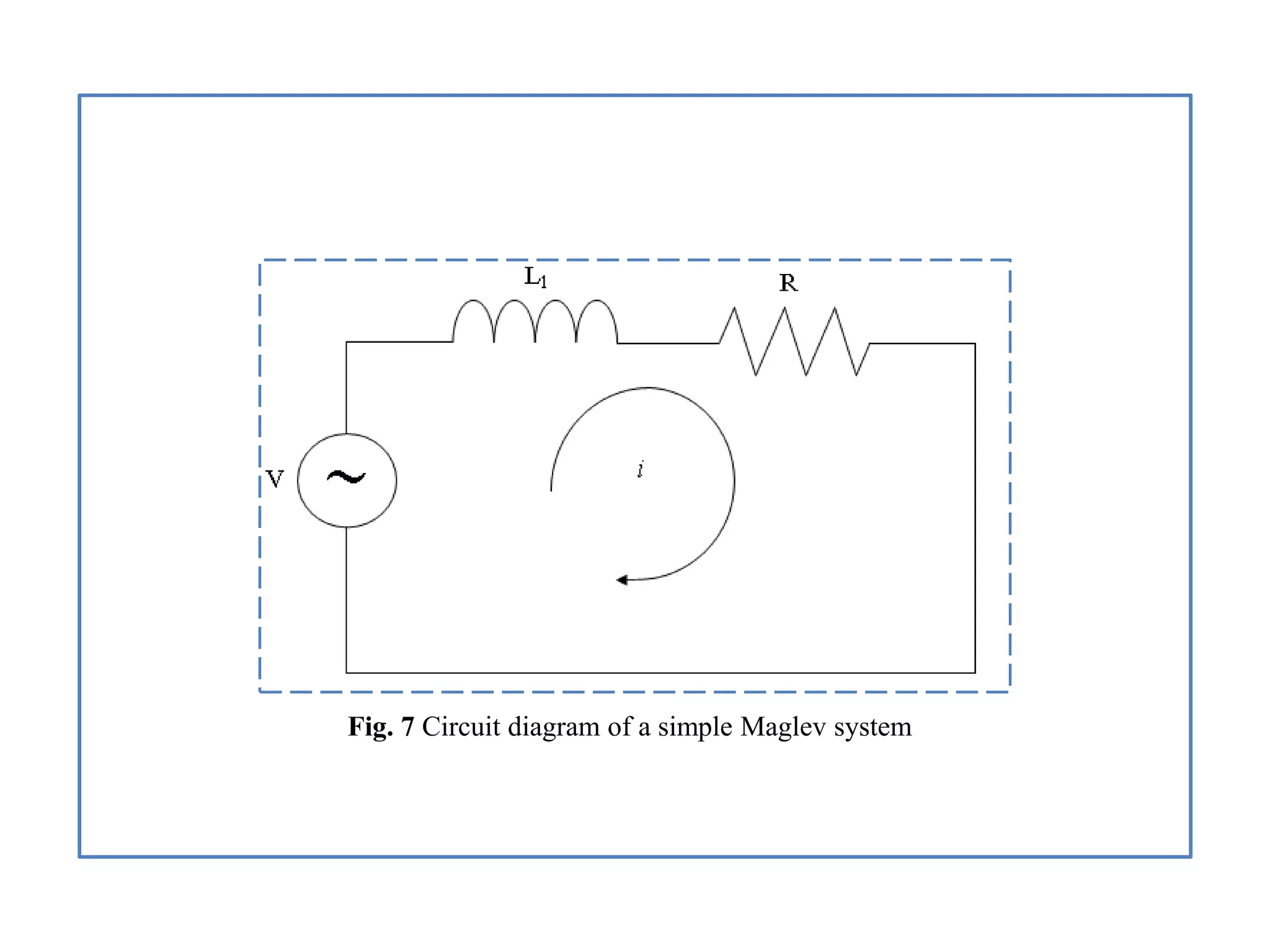
15. 4.1. General State-Space Transformation
Using the fundamental principle of dynamics,
We know from the law of mutual inductance that
A simple circuit diagram of the maglev system is shown in Figure 7. Applying
Kirchhoff's voltage law, we get,
As per Wong [2] the inductance is assumed to vary inversely with respect to ball's
position x.
Where x0 is the correction constant to incorporate the non-idealities in permeability.

16. Since it is well known that is approximately 25 times smaller than L1. Therefore, the
third term on the RHS can be neglected. Rewriting the above equation, we get,
Now we will do energy analysis on the system.
Energy stored in inductor (WL) =
Mechanical energy of the system (WM) =
Now we replace the existing variables with new variables as follows,

17. Upon replacing with the new variables mentioned in the previous slide, we get the
generalized state-space form of the equations as follows,

18. 4.2. Non-Linear Controller Approach
The assumption made in this approach constraints current and position are to always
have positive values which confirms that our transformation will be invertible [3].
Let new state variables be Z1, Z2, and Z3 denoting the the levitated ball's position,
velocity and acceleration respectively. Thus now, we can write the transformation as,
According to the state feedback control,
, and
Where,
[4]
[4]

19. The state-space representation of the non-linear controller or the exact linearization
controller is written as follows:
Let an arbitrary reference trajectory z1ref, z2ref, z3ref, and reference input jref (all the
four reference parameters are time dependent which should be quite obvious) such
that,
So, now the feedback control can be written as,
The non-linear controller feedback gains are chosen to ensure that the closed loop
poles of the system lie in the left-half plane.

20. 4.3. Linear Controller Approach
Cho et al. [4] did a comparison of sliding mode controller versus a linear controller.
They proved a better response from a sliding mode controller than the linear
controller. The MagLev system can be linearized by using the following
procedure[6]. Consider a nominal input voltage u0 producing nominal current x30=i0,
which levitates the ball to the equilibrium position x10=x0 and x20=v=0.
Using the Taylor's series expansion , we get,
Using above equations in the generalized state-space equation, we get,
At nominal operating point,
, and
Therefore,

21. Now, we will write all the equations together in a standard way as follows, and we
get the algebraic form of state-space equations for linear controller, which on the
next slide will be written in matrix form and along with the feedback term.

22. Where,
Where,

23. 5. MATLAB Application
All the necessary equations have been derived in the earlier.
Now we will mainly try to understand the technique to form Simulink diagrams.
Simulink file basically consists of blocks and can be stored in .slx (latest version)
format or the old conventional .mdl format.
There are many operations provided in the Simulink interface ranging from simple
math operations to highly complex integral operations. It also has the capability of
solving experimental data and plot graphs etc.
The next three slides will show the Simulink model’s diagrams.

24. 5.1. General Maglev System - Simulink Model
Fig. 8 Simulink block diagram for generalized system of equations for a simple maglev system

25. 5.2. Non-Linear Controller - Simulink Model
Fig. 9 Simulink block diagram for non-linear controller approach

26. 5.3. Simulink Block Diagram – u and x3 Determination
Fig. 10 Simulink block diagram used in finding voltage and current in the system

27. 6. Data Analysis and Results
 Simulink diagram – analyzed – two values of air gap.
 Distinct air gap – distinct operating frequency as well as amplitude.
 Air gap, Z1ref = A0 + A1sin(ωt)
 ω = 2πf
1st set values  A0=18.5 mm, A1=0.5 mm, and f=5 Hz
K0=2*106, K1=9,50,000, K2=80,000, and K3=900.
2nd set values  A0=14.0 mm, A1=0.3 mm, and f=10 Hz
K0=6*107, K1=3*106, K2=1,95,000 , and K3=1,050.
The next slides will include the analysis data and the latter part will have discussion
and conclusion.

28. 6.1. Simulink Graphs
0 0.5 1 1.5 2 2.5 3 3.5 4
0.018
0.0182
0.0184
0.0186
0.0188
0.019
0.0192
Signals
Time, t (second)
Z
1ref
,Z
1
(inmeter)
1 2 3 4 5 6 7
0
1
2
3
4
5
6
7
8
x 10
-5
Time, t (second)
(Z
1ref
-Z
1
)(inmeter)
Fig. 11 Reference and simulated ball
position for 18.5 mm mean air gap operated
at 5 Hz frequency and 0.5 mm amplitude.
Fig. 12 Difference between the reference
and the simulated position of the steel ball
for 18.5 mm mean air gap operated at 5 Hz
frequency and 0.5 mm amplitude.

29. 0 0.5 1 1.5 2 2.5 3 3.5 4
-0.02
-0.015
-0.01
-0.005
0
0.005
0.01
0.015
0.02
Time, t (second)
Z
2ref
,Z
2
(inm/s)
Fig. 13 Reference and simulated ball
velocity for 18.5 mm mean air gap operated
at 5 Hz frequency and 0.5 mm amplitude.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5
0
0.5
1
1.5
2
2.5
3
3.5
x 10
-3
Time, t (second)
(Z
2ref
-Z
2
)(inm/s)
Fig. 14 Difference between the reference
and the simulated velocity of the steel ball
for 18.5 mm mean air gap operated at 5 Hz
frequency and 0.5 mm amplitude.

30. 0 1 2 3 4 5 6 7 8
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Time, t (second)
Z
3ref
,Z
3
(inm/s2)
Fig. 15 Reference and simulated ball's
acceleration for 18.5 mm mean air gap
operated at 5 Hz frequency and 0.5 mm
amplitude.
0 1 2 3 4 5 6 7 8 9
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
Time, t (second)
(Z
3ref
-Z
3
)(inm/s2)
Fig. 16 Difference between the reference
and the simulated acceleration of the steel
ball for 18.5 mm mean air gap operated at 5
Hz frequency and 0.5 mm amplitude.

31. 0.5 1 1.5 2 2.5 3 3.5 4 4.5
0.0138
0.0138
0.0139
0.0139
0.014
0.014
0.0141
0.0141
0.0142
Time, t (second)
Z1ref,Z1(m)
Fig. 17 Reference and simulated ball position
for 14.0 mm mean air gap operated at 10 Hz
frequency and 0.3 mm amplitude.
0 0.5 1 1.5 2 2.5 3 3.5
0
1
2
3
4
5
x 10
-5
Time, t (second)
(Z
1ref
-Z
1
)(meter)
Fig. 18 Difference between the reference
and the simulated position of the steel ball
for 14.0 mm mean air gap operated at 10
Hz frequency and 0.3 mm amplitude.

32. 1 2 3 4 5 6
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
Signals
Time, t (second)
Z
2ref
,Z
2
(inm/s)
Fig. 19 Reference and simulated ball's
velocity for 14.0 mm mean air gap operated
at 10 Hz frequency and 0.3 mm amplitude.
1 2 3 4 5 6 7
5.4
5.6
5.8
6
6.2
6.4
6.6
x 10
-3
Time, t (second)
(Z
2ref
-Z
2
)(inm/s)
Fig. 20 Difference between the reference and
the simulated velocity of the steel ball for
14.0 mm mean air gap operated at 10 Hz
frequency and 0.3 mm amplitude.

33. 1 2 3 4 5 6 7 8
-5
-4
-3
-2
-1
0
1
2
3
4
5
Time, t (second)
Z
3ref
,Z
3
(inm/s2)
Fig. 21 Reference and simulated ball's
acceleration for 14.0 mm mean air gap operated
at 10 Hz frequency and 0.3 mm amplitude.
1 2 3 4 5 6 7 8
0.4
0.6
0.8
1
1.2
1.4
Time, t (second)
(Z
3ref
-Z
3
)(inm/s2)
Fig. 22 Difference between the reference
and the simulated acceleration of the steel
ball for 14.0 mm mean air gap operated at
10 Hz frequency and 0.3 mm amplitude.

34. 0 1 2 3 4 5 6 7
-25
-20
-15
-10
-5
0
Time, t (second)
Voltage,u(inVolt)
Fig. 23 Voltage signal supplied to the Maglev System
when the mean air gap was maintained at 18.5 mm
and the vibration motion of the levitated mass
occurred at 5 Hz frequency having 0.5 mm
amplitude.
1 2 3 4 5 6 7
-40
-30
-20
-10
0
10
20
Time, t (second)Voltage,u(inVolt)
Fig. 24 Voltage signal supplied to the
Maglev System when the mean air gap was
maintained at 14.0 mm and the vibration
motion of the levitated mass occurred at 10
Hz frequency having 0.3 mm amplitude.

35. 74 76 78 80 82 84 86 88 90
-0.8
-0.7
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
Time, t (second)
Current,X
3
(inAmpere)
Fig. 25 Current flowing in the electromagnet
when the mean air gap was maintained at 18.5
mm and the vibration motion of the levitated
mass occurred at 5 Hz frequency having 0.5
mm amplitude.
76 78 80 82 84 86 88 90
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
Time, t (second)
Current,X
3
(inAmpere)
Fig. 26 Current flowing in the electromagnet
when the mean air gap was maintained at 14.0
mm and the vibration motion of the levitated
mass occurred at 10 Hz frequency having 0.3
mm amplitude.

36. 0.5 1 1.5 2 2.5 3 3.5 4 4.5
-2000
-1500
-1000
-500
0
500
1000
1500
2000
Time, t (second)
FeedbackLinearizationSignal(w)
Fig. 27 Effect of noise on this system.
Comparison of the Feedback Linearization
signal (w) when the mean air gap was set at
18.5 and 14.0 mm with their respective
amplitude and frequency of vibration.

37. 6.2. Results and Discussion
 Figure 12 and Figure 18 – when instantaneous air gap = mean air gap  error
(Z1ref -Z1)  minimum or Zero.
 In Figure 11, 12, 17, and 18 - maxima/minima results after a stipulated time which
depends upon the frequency of operation.
 These maximas/minimas form a locus - straight lines - slope = constant in
magnitude but can be positive or negative.
 Figure 13, 19 - at mean position the value of simulated velocity ≈ reference
velocity.
 Figure 14, 20 - near the extreme ends - (Z2ref -Z2) increases and decreases with
time and so on. Here too straight lines can show the locus of velocities near extreme
ends.

38.  The velocity of ball requires numerical differentiation, which amplifies the noise
occurring during position measurement. The noise must be eliminated very carefully
using a proper filter to avoid the delay in estimate and to avoid degradation of system
performance or else the smallest of the disturbance can make the system unstable.
Moreover, this is the reason why there is a steep increase/decrease in acceleration
of the ball after some time regularly (shown in Figure 15, 16, 21, 22). Obviously,
it is because of the nature of working of the controller.
 The variation of L with respect to x is neglected. L0x0/x < 25(L1).
 Overall uniformity, gentle slope nature, and greater repeatability of plot(s)
obtained when the mean air gap was maintained at 14.0 mm with frequency 10 Hz as
compared to mean air gap 18.5 mm and frequency 5 Hz.
 Thus for our controller approach, 10 Hz frequency of operation seemed to give
more pleasant results because of the fact that the controller could vary the current
and thus the electromagnetic force exerted on the ball more frequently, thus keeping
the system out of unstable zone.
 Figure 23, 24 shows that when the mean air gap is equal to 18.5 mm and the
frequency of operation is 5 Hz and amplitude is 0.5 mm, the voltage supplied is
negative throughout, unlike the case of 14.0 mm mean air gap where the voltage
ranges between 12 to -36 Volts. So the earlier case will be relatively unstable.

39.  This clearly shows that the second set of results (mean air gap = 14.0 mm,
frequency=10 Hz and amplitude = 0.3 mm) are more stabilized. Hence, the working
range for our model must be near 14.0 mm and above 10.0 mm.
 Figure 25, 26 has no regular and simple nature.
 The feedback signal versus time shown in Figure 28 has a simple and regular
pattern for the first set of data (i.e. 18.5 mm mean air gap). Whereas the second set
(i.e. 14.0 mm mean air gap) shows a gradual increasing and/or decreasing nature and
the magnitude of the feedback signal is larger for the second set of data.

40. 6.3. Conclusions
This report presents the algebraic transformations and Simulink model formulation
of a simple Maglev system. We demonstrated the effectiveness of feedback
linearization approach namely nonlinear control theory by examining the kinematic
parameters (position, velocity, acceleration) and their errors with respect to the
reference values. The current, voltage and feedback signal were also examined. The
bottom line for this experiment is that the operating/stable range lies near 14.0 mm
(>10.0 mm) with frequency of operation 10 Hz (>5 Hz) and amplitude of vibration
equal to 0.3 mm (<0.5 mm). The operating range for Maglev systems is very
important and the same implies to the type of feedback control approach used. This
is particularly important in systems where large deviations are expected and where
the mean air gap must remain unaffected (almost) under interaction with external
disturbances (noise). However, the system we made is satisfactorily acceptable under
circumstances without noise signal. Moreover, the system can be improved to the
extent of practical, robust application iff one has the knowledge of advanced, and
complex controller approaches.

41. References
[1] Siscoe, G. L. (1986). "An historical footnote on the origin of 'aurora
borealis'", History of Geophysics: Vol. 2,. p. 11. ISBN 0-87590-276-6.
[2] Wong,T., 1986, Design of a magnetic levitation system-an undergraduate
project, IEEE Transactions on Education, 29,196-200.
[3] Isidori, A., 1989, Nonlinear Control Systems, New York: Springer-Verlag.
[4] Krener, A., and Respondek, W., 1985, Nonlinear observers with
linearizable error dynamics, SIAM Journal on Control and Optimization.
[5] Cho, D., Kato, Y., Spilman, D., 1993, Experimental comparison of sliding
mode and classical controllers in magnetic levitation systems, IEEE
Control Systems.
[6] Krener, A., and Isidori, A., 1983, Linearization by output injection and
nonlinear observers, System and Control Letters, 3, 52-57.