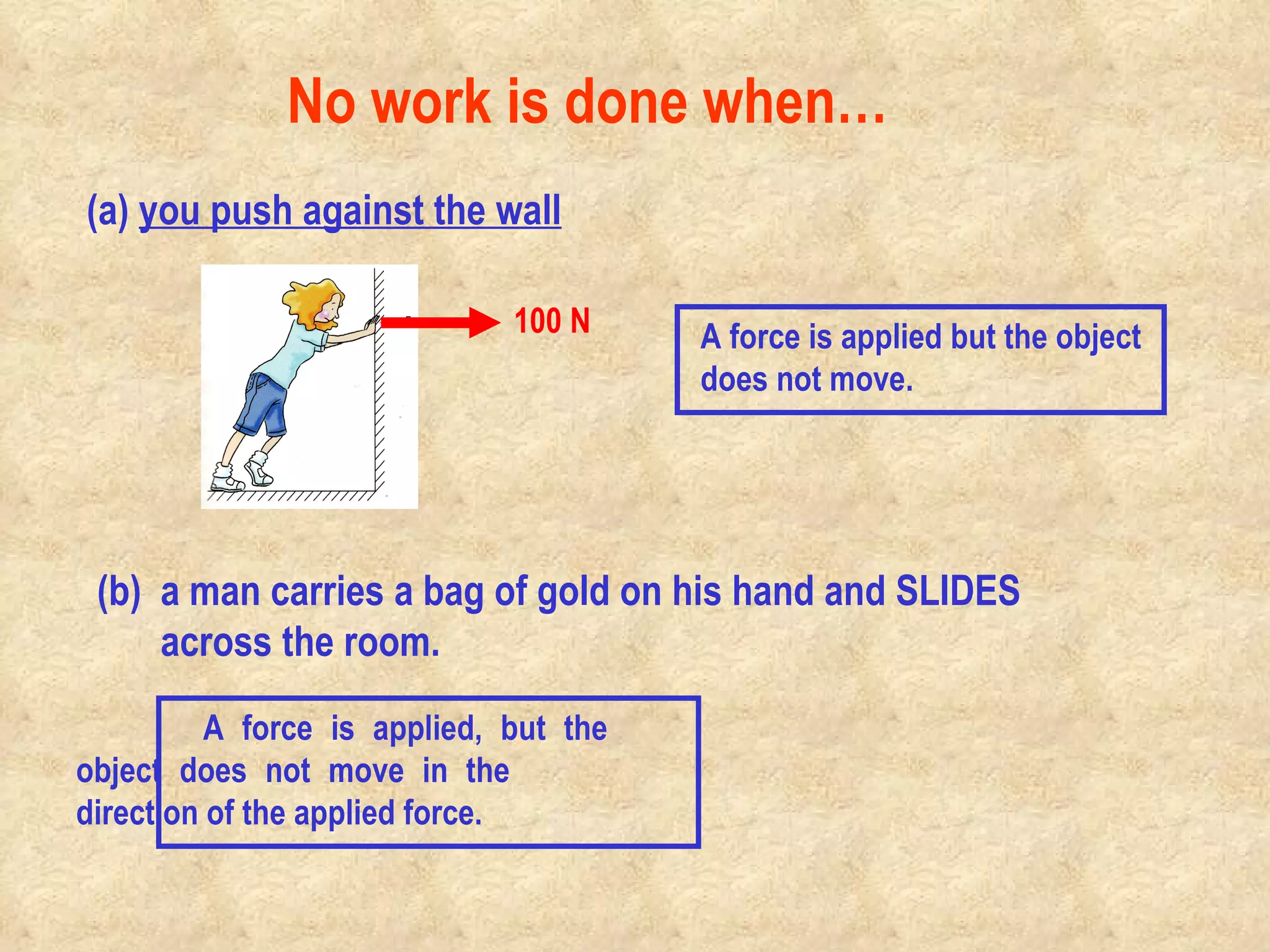
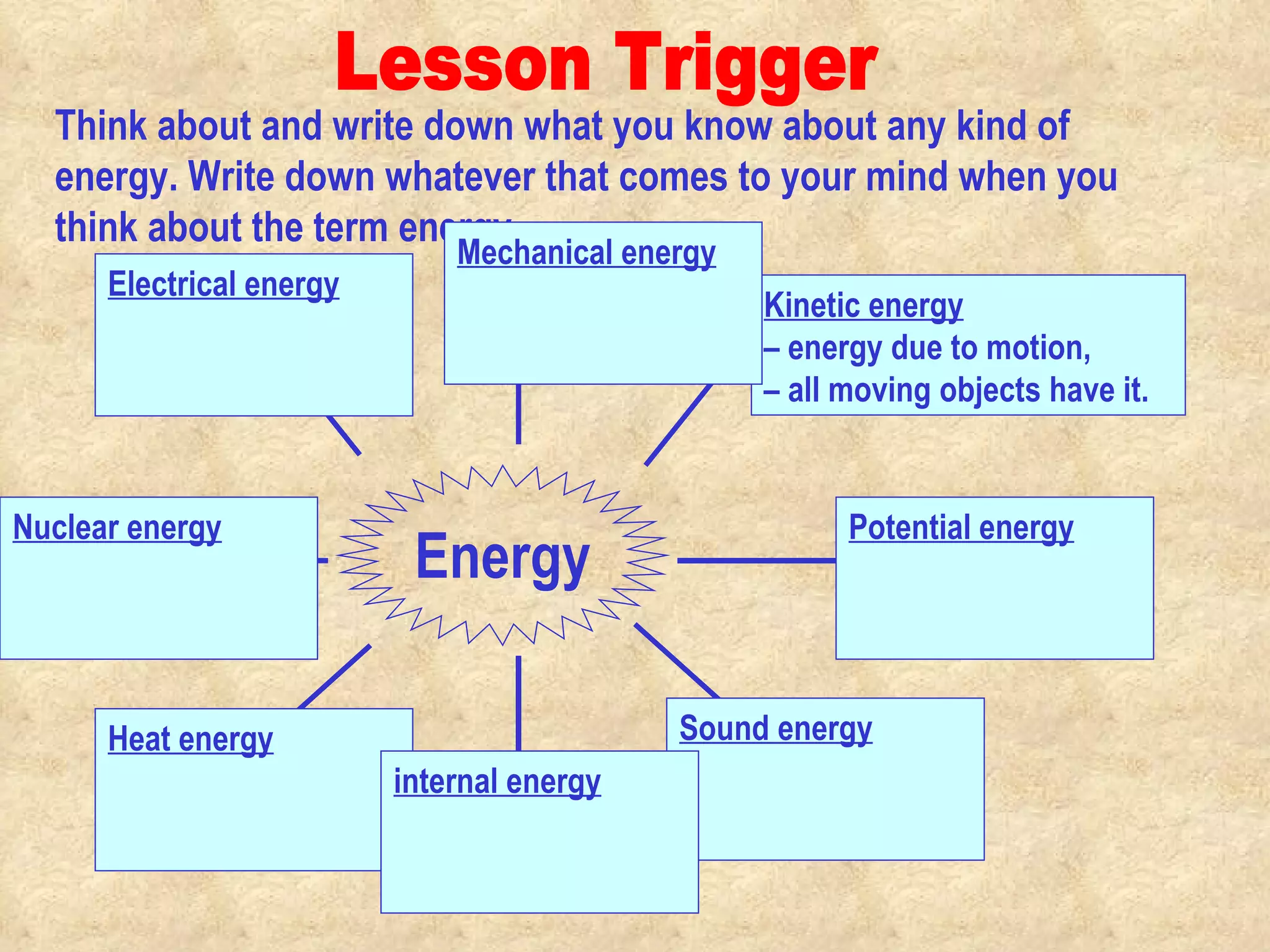
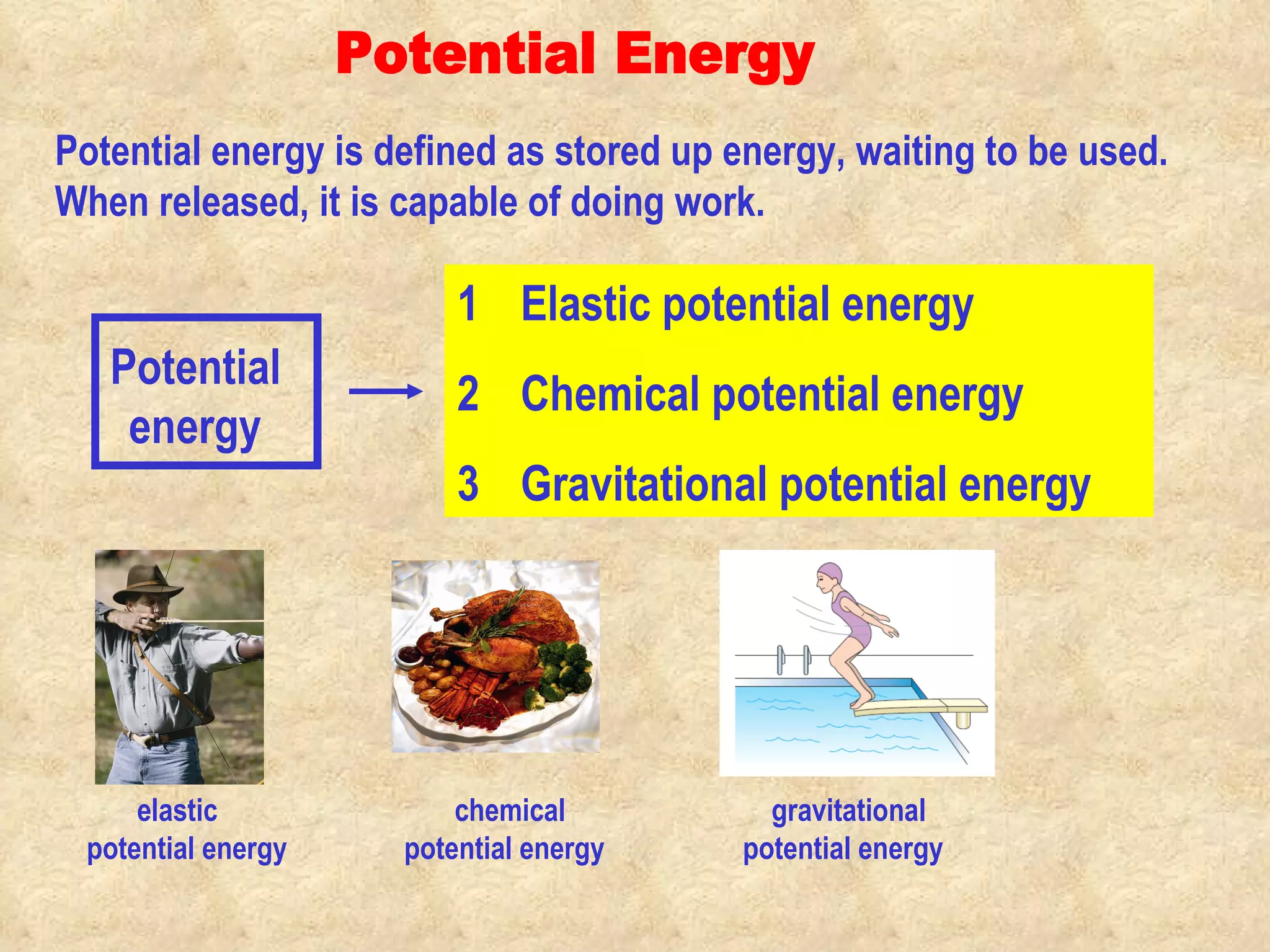
1) Work is done when a force causes an object to move in the direction of the force. Different types of energy include kinetic, potential, chemical and thermal.
2) The principle of conservation of energy states that energy cannot be created or destroyed, only converted from one form to another.
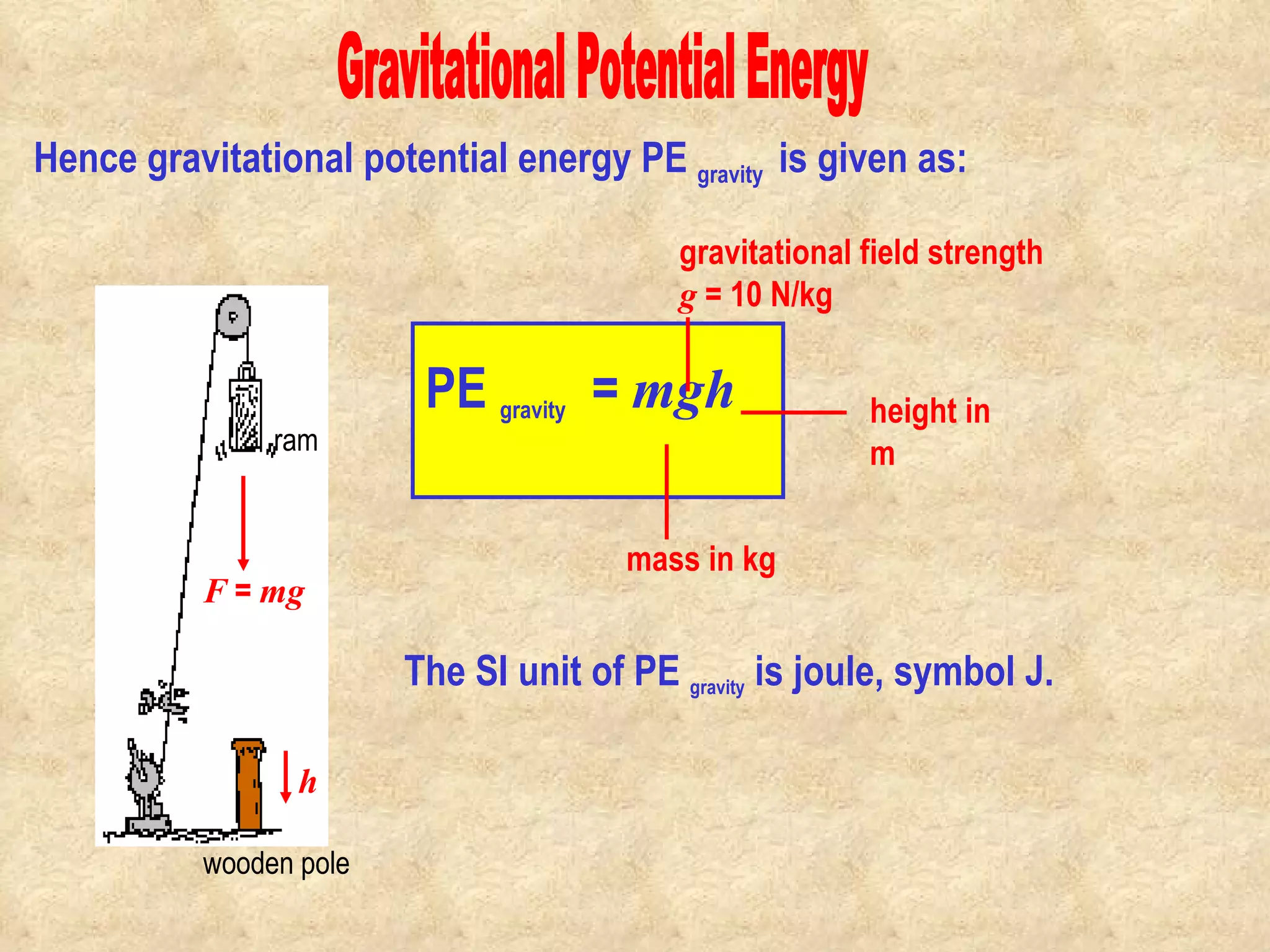
3) Kinetic energy is defined as E_k=1/2mv^2 and gravitational potential energy as E_p=mgh. These relationships can be used to solve problems involving work, energy and power.