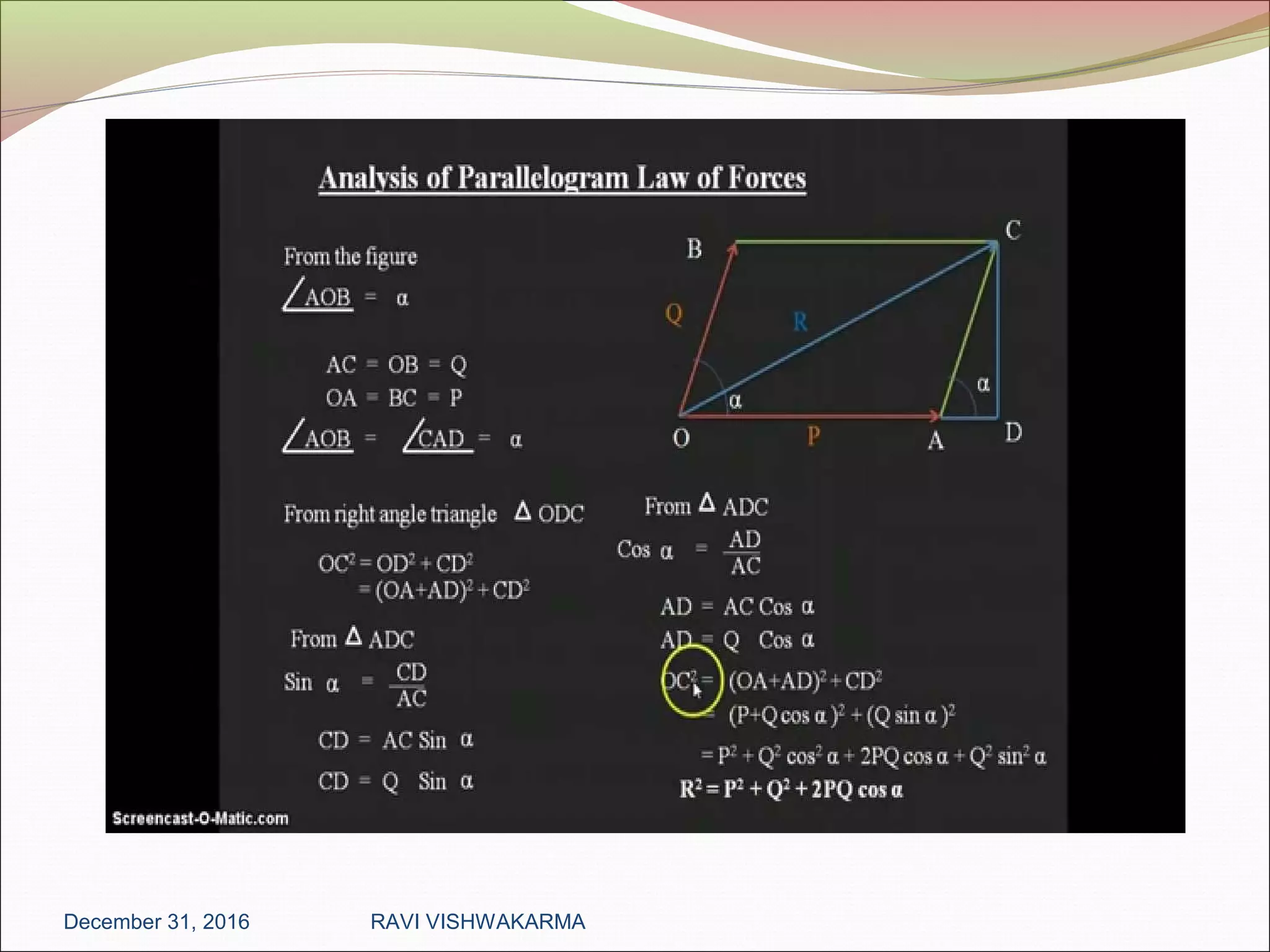
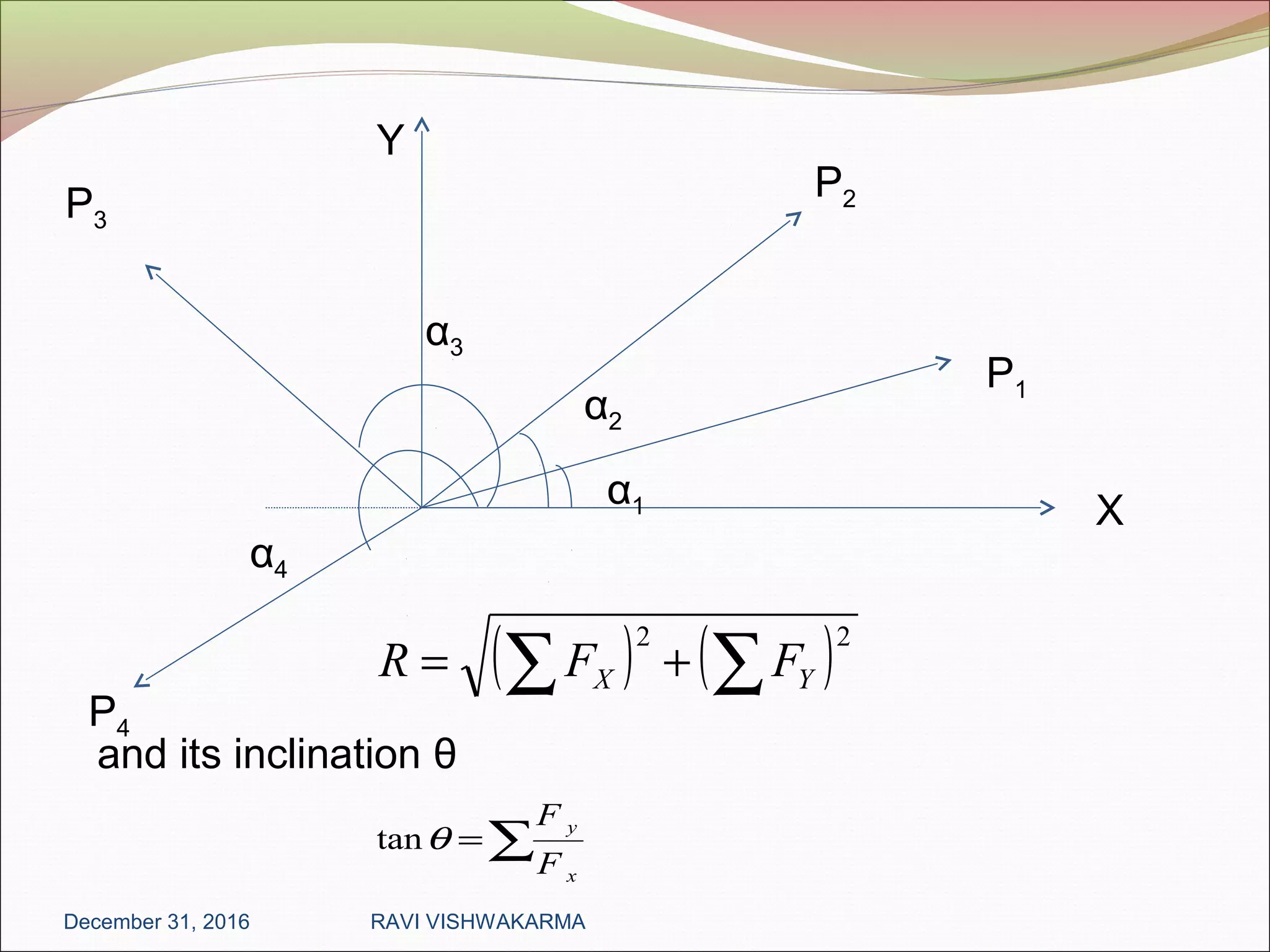
The document outlines fundamental concepts of mechanical engineering, focusing on force systems, concurrent forces, moments, and principles like Lami's theorem and Varignon’s theorem. Key topics include the definitions of force, moment of force, couples, resolution of forces, free body diagrams, center of gravity, centroids, and moment of inertia. It serves as a comprehensive guide to understanding the elements and calculations of mechanical forces and their effects.

1. JAHANGIRABAD INSTIUTE OF TECHNOLOGY
BARABANKI
Department of Mechanical Engineering
Elements of Mechanical Engineering
December 31, 2016 RAVI VISHWAKARMA

2. CONTENTS
1. Force System
2. Law of Parallelogram
3. Collinear forces
4. Concurrent Forces
5. Lami's Theorem
6. Principle of Transmissibility
7. Moment of Force
8. Couple
9. Varignon’s Theorem
10. Resolution of force
11. Resultant of Coplanar –Concurrent force
12. Free Body Diagram
13. Center of gravity & Centroid
14. Moment of Inertia
December 31, 2016 RAVI VISHWAKARMA

3. Force System
If all the forces in a system lie in a single plane through a single
point, they constitute a coplanar concurrent force system. it is
possible to find a single force which will have the same effect as
that of number of force acting. Such single force is called
Resultant force and the process of finding the resultant force is
called composition of forces.
December 31, 2016 RAVI VISHWAKARMA

4. Force
1) Force is a push or pull.
2) Force is the capacity to do work or cause physical
change.
3) Force= Mass times acceleration (F = ma)
4) A force is that which changes or tends to change the state
of rest or motion of a body.
December 31, 2016 RAVI VISHWAKARMA

5. Law of Parallelogram
This law is applicable to determine the resultant of two
coplanar concurrent forces only. This law states ―If two
forces acting at a point are represented both in magnitude
and direction by the two adjacent sides of a parallelogram,
then the resultant of the two forces is represented both in
magnitude and direction by the diagonal of the
parallelogram passing through the same point.”
December 31, 2016 RAVI VISHWAKARMA

6. December 31, 2016 RAVI VISHWAKARMA

7. Collinear forces
Forces have the same line of action.
May act in same or different directions.
December 31, 2016 RAVI VISHWAKARMA

8. Collinear forces
Forces have the same line of action.
May act in same or different directions.
December 31, 2016 RAVI VISHWAKARMA

9. Concurrent Forces
Forces do not act along same line, but do act through
the same point.
In physics, concurrent forces are defined as forces that
pass through a common point.
In other words,
a concurrent force system is a set of two or
more forces whose lines of action intersect at a point
at the same time.
December 31, 2016 RAVI VISHWAKARMA

10. Lami’s Theorem
If a body is in equilibrium under the action of only three
forces, each force is proportional to the sine of the angle
between the other two forces.
F2 F1
α
F3
γ
β
γβα sinsinsin
321 FFF
==
December 31, 2016 RAVI VISHWAKARMA

11. Principle of Transmissibility
States that the conditions of equilibrium or conditions of
motion of a rigid body will remain unchanged if a
force acting at a give point of the rigid body is
replaced by a force of the same magnitude and same
direction, but acting at a different point, provided that
the two forces have the same line of action.
December 31, 2016 RAVI VISHWAKARMA

12. Moment of Force
Moment of force about a point is the measure of rotational
effect of the force. Moment of a force about a point is
defined as the product of the magnitude of the force and
the perpendicular distance of the point from the line of
action of the force. The point about which the moment is
considered is called moment center and the perpendicular
distance of the point from the line of action of the force is
called moment arm.
December 31, 2016 RAVI VISHWAKARMA
d2
d1
F

13. Couple
A couple is a pair of forces, equal in magnitude,
oppositely directed, and displaced by perpendicular
distance or moment.
The simplest kind of couple consists of two equal and
opposite force whose lines of action do not coincide.
This is called a "simple couple". The forces have a
turning effect or moment called a torque about an
axis which is normal (perpendicular) to the plane of
the forces. The SI unit for the torque of the couple
is newton meter.
December 31, 2016 RAVI VISHWAKARMA

14. Varignon’s theorem
French mathematician Varignon(1654-1722) gave the
following which is also known as principles of moments:
The algebraic sum of moments of a system of coplanar
forces about a moment center is equal to the moment of
their resultant force about the same moment center.
December 31, 2016 RAVI VISHWAKARMA

15. Resolution of force
Finding the components of a given force in two given
direction is called resolution. These component forces will
have the same effect on the body as given single force.
P=R Cosα
Q=R Sin α
Q R
P X
Y
December 31, 2016 RAVI VISHWAKARMA

16. Resultant of coplanar –Concurrent forces
The analytical method is based on theorem of resolved
parts which states that
“ The algebraic sum of the resolved parts of two forces
in a given direction is equal to the resolved part of
their resultant in the same direction.”
December 31, 2016 RAVI VISHWAKARMA

17. α3
( ) ( )22
∑∑ += YX FFR
and its inclination θ
∑=
x
y
F
F
θtan
X
Y
P2P3
P4
α1
α2
α4
P1
December 31, 2016 RAVI VISHWAKARMA

18. Free Body Diagram
The force analysis of a structure is made in a simplified way
by considering the equilibrium of a portion of the
structure. For that, the portion is drawn separately
showing applied forces, self weight and reactions at the
point of contact with other bodies. The resulting diagram
is known as free body diagram.
In a FBD, all the supports (like walls ,floors, hinges etc) are
removed and replaced by the reactions which these
supported exert on the body.
Examples-…….
December 31, 2016 RAVI VISHWAKARMA

19. Center of Gravity
• The point at which all the mass of the body may be assumed to
be concentrated.
• The point through which the force of gravity is considered to
act vertically downwards, with a force equal to the weight of
the body. The point about which the body would balance. The
center of gravity of a homogeneous body is at its geometrical
center.
December 31, 2016 RAVI VISHWAKARMA

20. Centroids
The centroid of an area is situated at its geometrical centre. In
each of the following figures ‘G’ represents the centroid, and if
each area was suspended from this point it would balance.
December 31, 2016 RAVI VISHWAKARMA

21. Moment of Inertia
The product of the elemental area and square of the
perpendicular distance between the centroid of area and the
axis of reference is the “Moment of Inertia” about the reference
axis.
Ixx
= ∫dA. y2
Iyy
= ∫dA. x2
x
December 31, 2016 RAVI VISHWAKARMA
dA
Y
X
Y