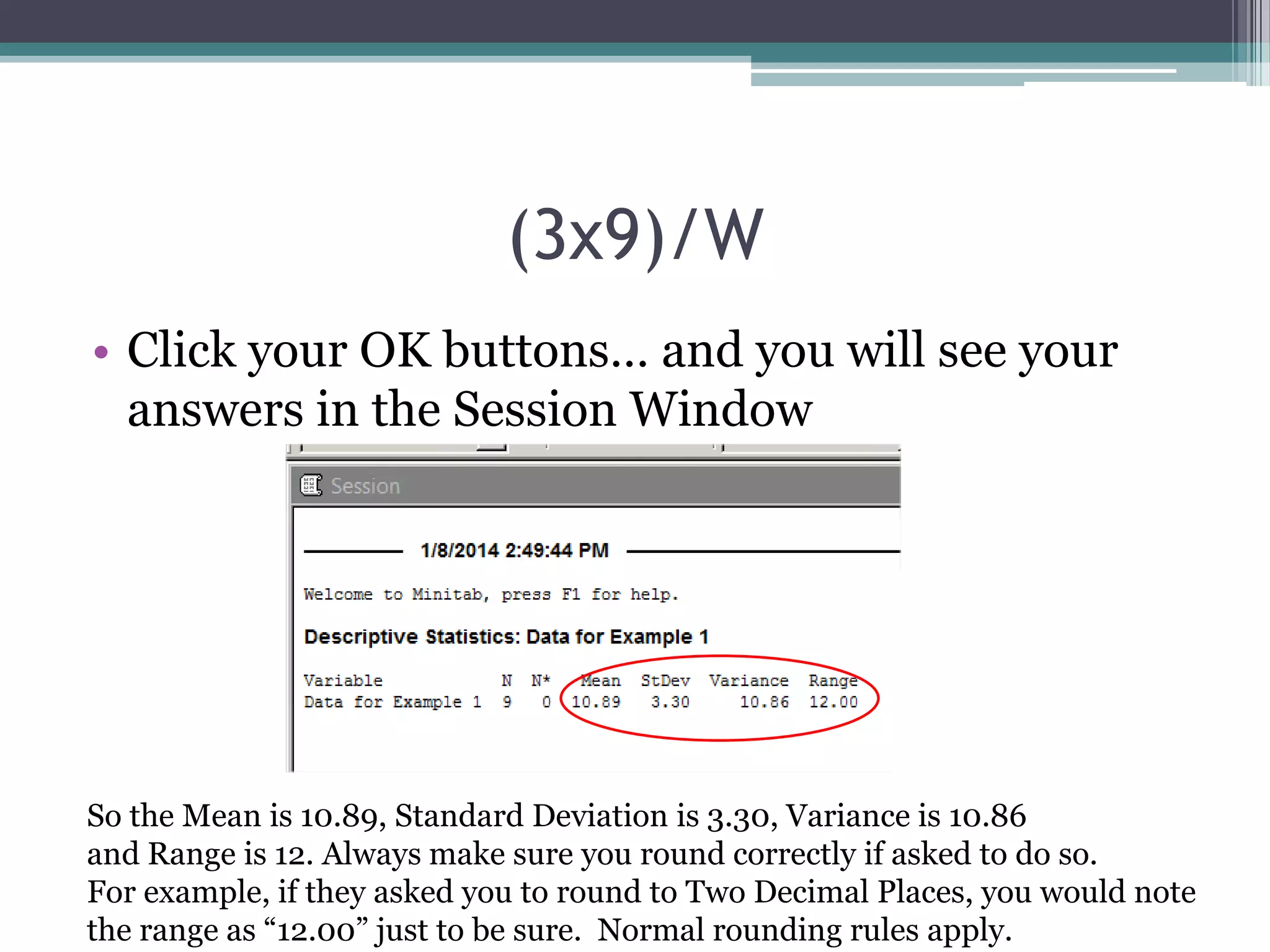
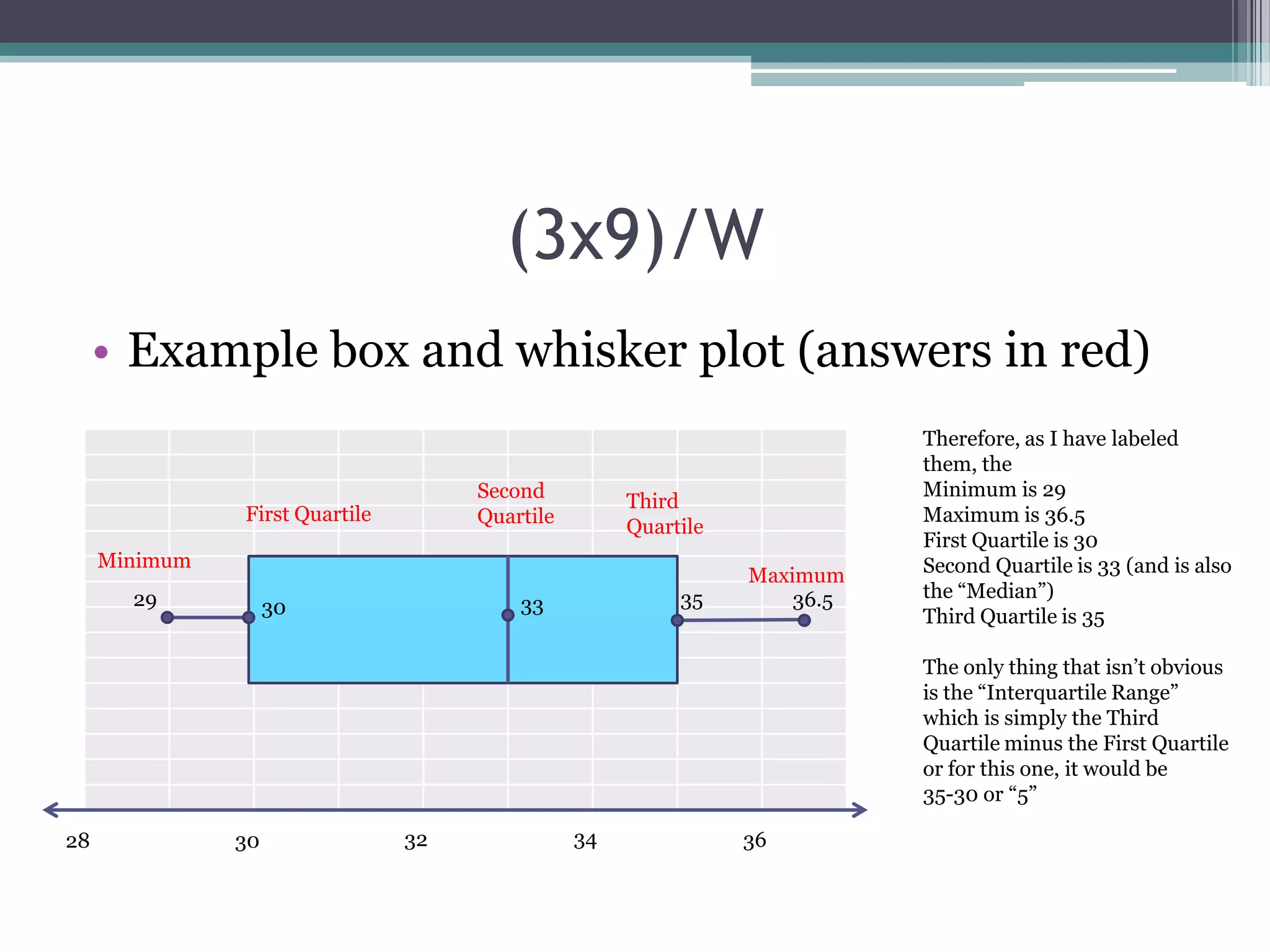
This document provides examples and explanations for 3 extra homework problems from a statistics class. (1) The first problem asks students to find the range, mean, variance and standard deviation for a sample data set using Minitab software. Step-by-step instructions are given. (2) The second problem involves interpreting parts of a box-and-whisker plot like minimum, maximum, and quartiles. (3) The third problem has students match z-scores to points on a histogram by considering where values above, below, or at the mean would fall. An unusual z-score is identified as well.

1. Week 1 3 Extra Homework
Examples (3x9)/W
MA 221
Statistics for Decision Making
Professor Brent Heard
Not to be copied or linked to
without my permission

2. (3x9)/W
• As noted, this term I will post three additional
homework examples by 9 PM (Mountain Time)
on Wednesday evening in the Statcave.
• (3x9)/W just means “3 by 9 PM on Wednesday.”
• This week, I will do problems similar to number
18, 22 and 24.

3. (3x9)/W
• Number 18 is a basic “Find the range, mean,
variance and standard deviation” type problem.
I will show you how to do one in Minitab easily.
• Please note that I change the numbers so I don’t
give the exact homework problem.

4. (3x9)/W
• Example for 18
▫ Find the range, mean, variance and standard
deviation of the sample data set.
9 12 5 13 12 10 9 17 11

5. (3x9)/W
• First go to Minitab (I access Minitab by going to
the iLab link under Course Home and then
follow the “Go to Citrix” link.)
• This term there seems to be a little different look
to it, but I still found Minitab in the Apps easily.

6. (3x9)/W
• Enter the data in the spreadsheet part of
Minitab. I labeled mine “Data for Example 1”

7. (3x9)/W
• At the top of Minitab, go to Stat >> Basic
Statistics >> Display Descriptive Statistics
Put your cursor in the Variables
box and click, then choose/
double click C1 on the left

8. (3x9)/W
• Now it should look similar to this based on what
you called your data

9. (3x9)/W
• Click the Statistics button and select/check what
you need from the menu that pops up…

10. (3x9)/W
• Click your OK buttons… and you will see your
answers in the Session Window
So the Mean is 10.89, Standard Deviation is 3.30, Variance is 10.86
and Range is 12. Always make sure you round correctly if asked to do so.
For example, if they asked you to round to Two Decimal Places, you would note
the range as “12.00” just to be sure. Normal rounding rules apply.

11. (3x9)/W
• Number 22 is a box and whisker plot type
problem and is actually very easy.
• By looking at a box and whisker plot, you are
asked to identify (a) the minimum, (b) the
maximum, (c) the first quartile, (d) the second
quartile, (e) the third quartile and (f) the
interquartile range.

12. (3x9)/W
• Example box and whisker plot (answers in red)
Second
Quartile
First Quartile
Third
Quartile
Minimum
29
35
33
30
Maximum
36.5
Therefore, as I have labeled
them, the
Minimum is 29
Maximum is 36.5
First Quartile is 30
Second Quartile is 33 (and is also
the “Median”)
Third Quartile is 35
The only thing that isn’t obvious
is the “Interquartile Range”
which is simply the Third
Quartile minus the First Quartile
or for this one, it would be
35-30 or “5”
28
30
32
34
36

13. (3x9)/W
• Number 24 is a histogram where we are
matching z scores to a place on the histogram.
• Don’t let this one worry you, it’s actually very
intuitive and easy.
• Let’s look at an example.

14. (3x9)/W
• Let’s say they want us to identify points A, B and
C with z scores. Our choices are:
z=0
z = -1.88
z = 3.20
Answers next page
16
21
26
31
36
41
46

15. (3x9)/W
• Let’s say they want us to identify points A, B and
C with z scores. Our choices are:
z=0
Why?
Think about it…
A z score of zero means you are right on
the mean. Look where B is and the
shape of the histogram. It looks very
symmetrical, thus the mean would be
toward the middle.
16
21
26
31
36
41
46

16. (3x9)/W
• Let’s say they want us to identify points A, B and
C with z scores. Our choices are:
z = -1.88
Why?
Think about it…
A negative z score means you are that
many standard deviations “below” the
mean. So with this close to symmetric
histogram, it would be on the “left” side.
16
21
26
31
36
41
46

17. (3x9)/W
• Let’s say they want us to identify points A, B and
C with z scores. Our choices are:
z = 3.20
Why?
Think about it…
Positive z scores are that many
standard deviations “above” the mean.
So it has to be on the right side.
16
21
26
31
36
41
46

18. (3x9)/W
• Last question, “Are there any z scores that are
unusual?”
• YES, the z score of 3.20 would be considered
unusual because it is more than two standard
deviations away from the mean.
• z scores less than -2.00 (for example -2.02, -3.11,
etc.) or greater than 2.00 (for example 2.14, 2.01,
4.19, etc.) are “MORE than two standard deviations
away from the mean)

19. (3x9)/W
• Hope you enjoyed this…
• More examples next week….