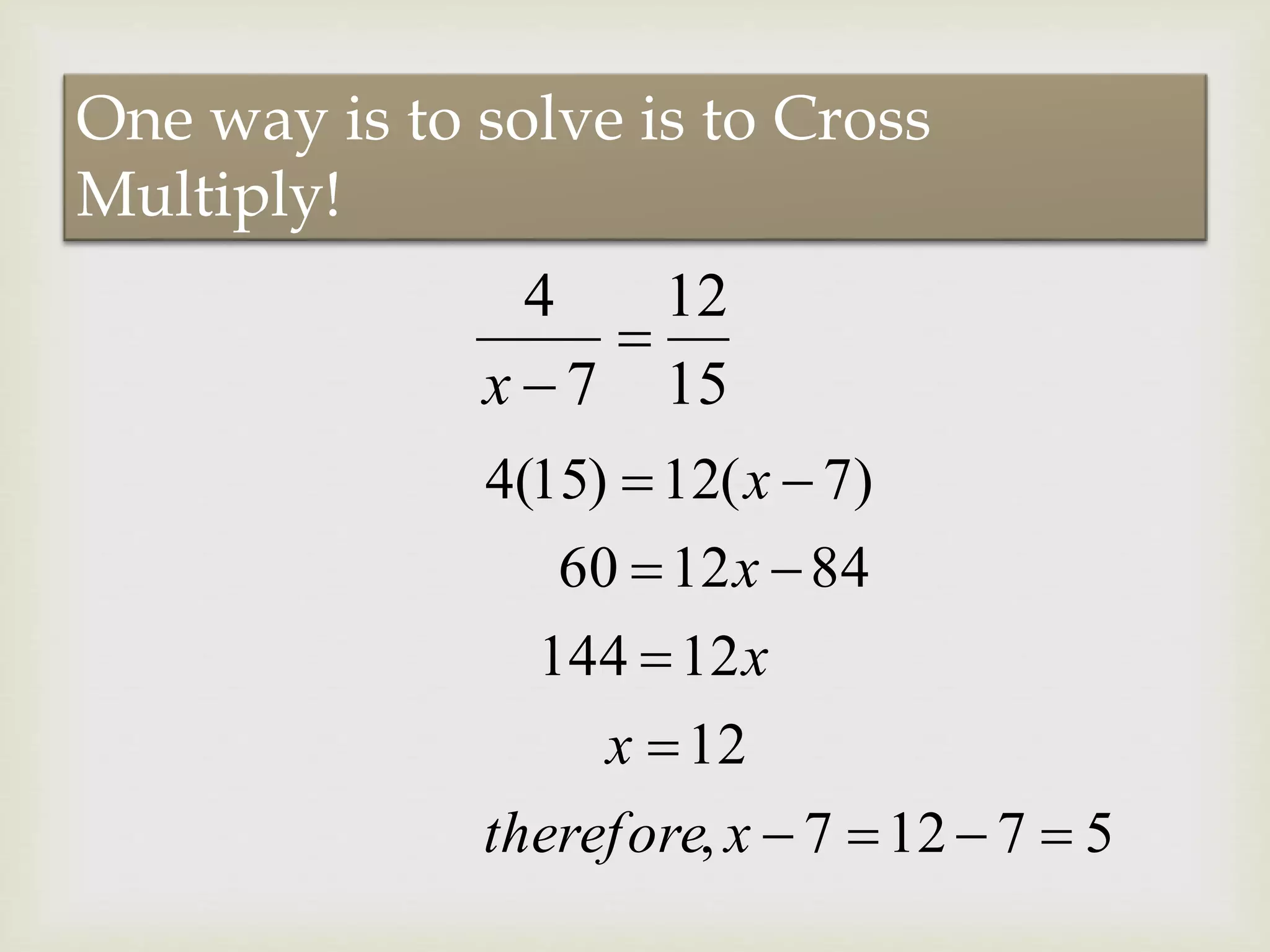The document provides information and examples about solving rational equations. It discusses that a rational equation contains one or more rational expressions. It then provides two main methods for solving rational equations - cross multiplying and finding the least common denominator. Several steps are outlined for using the least common denominator method, including finding the common denominator, clearing denominators by multiplying both sides by the LCM, solving the resulting equation, and checking solutions. Examples of using both methods to solve rational equations are shown. Additional resources for learning more about solving rational equations are also provided.

1. Can the student solve rational equations?

2. A rational equation is an equation that has one
or more rational expressions.
Examples:
Rational Equations
3
21


xx xx
x
x
x
2
1
1
3
3
2






3. 15
12
7
4

x
One way is to solve is to Cross
Multiply!
57127,
12
12144
841260
)7(12)15(4





xtherefore
x
x
x
x

4. xx
3
2
5


3
62
635
)2(3)(5




x
x
xx
xx
Check your work! 11,,
3
3
5
5
 becauseyes

5. 
Another way to Solving Rational
Eqns.
4. Check the solutions.
3. Solve the resulting equation.
2. Clear denominators by multiplying both
sides of the equation by the LCM.
1. Find the common denominator.
To solve a rational equation:

6. 













x
xx
x
xx
3
)2)((
2
5
)2)((
xx
3
2
5


The LCD is x(x+2)
Multiply both sides by this.
Now Simplify
3
62
635
)2(35




x
x
xx
xx

7. 
Easy example:
xx
12
2
13

LCD: 2x
Multiply each fraction
through by the LCD xx
12
2
13

2x2x2x
x
xx
x
x 24
2
26

246  x
18 x
18x

8. 
Factor denominator
Distribute and
set equal to zero.
Factor and solve
The LCM is (x – 3)(x – 5).
x2 – 8x + 15 = (x – 3)(x – 5)
x(x – 5) = –6
x2 – 5x + 6 = 0
(x – 2)(x – 3) = 0
x = 2 or x = 3
Check. x = 3 is not a solution since both sides would be undefined.
)5)(3(
6
3 


 xxx
x












 )5)(3(
6
3 xxx
x )5)(3()5)(3(  xxxx
Example: .
158
6
3 2



 xxx
x
)5)(3()5)(3(  xxxx

9. 9
12
3
3
3
2
2




 mmm
equationthistosolutionnoistheremSince
m
mm
mm
m
mm
m
mm
m
mm
,3
3m
3m
1215
129362
12)3(3)3(2
9
12
)3)(3(
3
3
)3)(3(
3
2
)3)(3( 2












Recall that you can not divide by 0. So from the original
Equation you see that m = 3 and m = -3
m2 – 9 factors to (m+3)(m-3), therefore our LCD is (m+3)(m-3)

10. 
If R is the total resistance for a parallel circuit with two
resistors of resistances, r1 and r2 , then .
Find the resistance, r1, if the total resistance, R, is 25
ohms and r2 is 95 ohms.
Round your answer to the nearest ohm if necessary.
21
111
rrR

34
9286.33
47514
1
475
14
1
95
1
25
1
95
11
25
1
1
1
1
1
1
1






r
r
r
r
r
r
Word Problem

11. 5
21
4
1 rr 


3
1
x
Examples Answer
4
18
10
24





x
x
x
x
3x
2
7
5
3
10

yy
5x
63
5
9
11
2
4


 mm 11
1
x

12. 
 http://www.purplemath.com/modules/solvrtnl2.ht
m
 http://www.algebra-online.com/solving-rational-
equations-3.htm
 https://www.khanacademy.org/math/algebra2/rati
onal-expressions-equations-and-functions/solving-
rational-equations/v/ex-1-multi-step-equation
Additional Resources