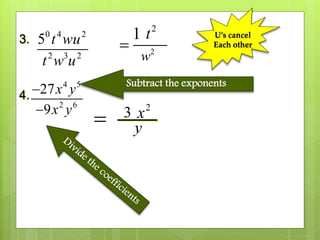
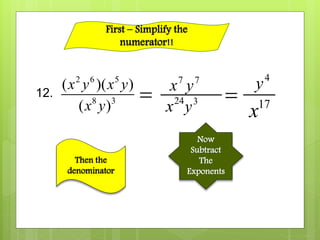
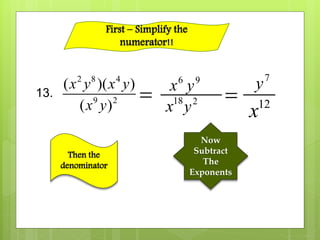
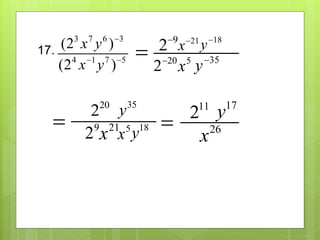This document provides an overview and examples for multiplying and dividing monomials with exponents. It defines key terms like monomial, base, and exponent. It explains the product rule for multiplying monomials by adding exponents of the same base. It also explains how to divide monomials by subtracting the exponents of the same base or changing the sign of negative exponents. The document includes 17 examples of multiplying and dividing monomials using these rules.

1. Ultimate Guide to
Multiplying & Dividing
Monomials with
Exponents

2. Monomials
 Multiplying &
Dividing Monomials
 Applying Exponent
Rules to Monomials

3. Vocabulary
 Monomials - a number, a variable, or a product of a number
and one or more variables
4x, 20x2yw3, -3, a2b3, and 3yz are all monomials.
 Constant – a monomial that is a number without a variable.
 Base – In an expression of the form xn, the base is x.
 Exponent – In an expression of the form xn, the exponent is
n.

4. Writing Expressions Using Exponents
Write the expression with exponents
(as multiplication):
8a3b38 ● a ● a ● a ● b ● b ● b =
Could the above expression be
written as a power of a product?
( )x
x x x x y  y y y
xy xy xy xy xy 4
or

5. Simplify the following expression: (5a2)(a5)
Step 1: Write out the expressions in expanded form.
Step 2: Rewrite using exponents.
Product Rule
5a
2
 a
5
  5 a  a  a a  a  a a
How many terms are there?
What operation is being performed? Multiplication!
5a
2
 a
5
  5 a
7
 5a
7

6. Multiplying Monomials: The Product Rule
4) 3k
5
mn
4
 7k
3
m
3
n
3
 
5) 12 x
2
y
3
 2xy
2
  24x3
y5
21k8
m4
n7
If the monomials have coefficients, multiply
those, but still add powers of common bases.

7. If the monomial inside the parentheses has more than one
variable, raise each variable to the outside power using
the power of a power rule.
(ab)m = am•bm
(9xy)2 = (-5x)2 = -(5x)2 =

8. Simplify the following: ( x3 )4
Note: 3 x 4 = 12
The monomial is the term inside the parentheses.
1. Multiply the exponents, write the simplified monomial
x
3
 
4
 x
12
For any number, a, and all integers m and n, am
 
n
 amn
.
1) b
9
 
10
 b90
2) c
3
 
3
 c9

9. 1) 2b
9
 
3
 8b27
2) 5c
3
 
3
 125c9
3) 7w
12
 
2
 49w24
If the monomial inside the parentheses has a
coefficient, raise the coefficient to the power, but still
multiply the variable powers.

10. Dividing
Monomials

11. For all integers “m” and “n” and any nonzero
number “a” ……
Let's review the rules.
m
n
a
a
m n
a 

When the problems look like this,
and the bases are the same, you will
subtract the exponents.
0
1a 
ANY number raised to the zero power
is equal to ONE.
n
a 1
n
a

If the exponent is negative, it is written
on the wrong side of the fraction bar,
move it to the other side, and change the
sign.

12. 1.
3 2 2
f g h
fgh
 3 1 2 1 2 1
f g h  
  2 1 1
f g h 
2.
3 5
7
24
6
x y
xy
Subtract the exponents
 4 2
x
2
y
Reminder: Never finish a
problem with negative
exponents

13. 3. 0 4 2
2 3 2
5 t wu
t w u
1

4.
4 5
2 6
27
9
x y
x y


Subtract the exponents
 3 2
x
y
U’s cancel
Each other
2
t
2
w

14. 5.
9 3
6 2
x y
xw u
 
Remember, if the exponent is negative, move it to the
other side of the fraction bar and make it positive.
 1
10
x 6 2 3
w u y
6.
6
8
x
x

  6
x
8
x
Now
Subtract
The
Exponents
 
2
x
1
2
x

15. 7.
6
3
40
10
x
x
Fix the
negative
exponent

6
40x
10
3
x 
Now divide the coefficients but ADD the exponents
4 9
x
1
 9
4x
8.
0 8 4 6
6 2
5 x w u
xw u

ANY number raised to the zero power is
equal to ONE.
1 7
x 2
w
4
u

16. 9.
10 2 16
5 6 4
30
5
x y z
x y z

 
Fix the
negative
exponents
 30
5
5
x
10
x
2 16
y z
6
y
4
z

Now divide the coefficients and combine the exponents
6
5
x 4
y
20
z

17. 10. 54
3
b
c
 
 
 
20
15
b
c

11.
2
9 3
6
v
w
 
 
 
6
v
 4
w

18. 2 6 5
8 3
( )( )
( )
x y x y
x y
12. 
7
x 7
y
Then the
denominator
24
x 3
y
Now
Subtract
The
Exponents

4
y
17
x
First – Simplify the
numerator!!

19. 2 8 4
9 2
( )( )
( )
x y x y
x y
13. 
6
x 9
y
Then the
denominator
18
x 2
y
Now
Subtract
The
Exponents

7
y
12
x
First – Simplify the
numerator!!

20. 14.
45 4 0
4 3 3
7
5
a b c
a b c

 
 
 
Exponents OUTSIDE
And INSIDE …… Distribute!!

4
( 7)
 20
a 16
b 0
c
4
5 16
a 12
b 12
c 
Fix your
Negative exponents
4
( 7)
4
5
20
a
16
a
16
b
12
b 12
c0
c

4
5
4
7
4
a 4
b
12
c
Now
Subtract
The
Exponents

21. 15.
64 3 0
2 2 4
4
3
a b c
a b c

 
 
 
Exponents OUTSIDE
And INSIDE …… Distribute!!

6
( 4)
 24
a 18
b 0
c
6
3 12
a 12
b 24
c 
Fix your
Negative exponents
6
( 4)
6
3
24
a
12
a
18
b
12
b 24
c0
c

6
3
6
4
12
a 6
b
24
c
Now
Subtract
The
Exponents

22. 16.
3 5 4 2
5 1 5 4
(4 )
(4 )
x y
x y

 

6
4 10
x 8
y
20
4 4
x 20
y
 6
4
20
4
10
x 4
x
8
y
20
y

14
4
14
x
12
y

23. 17.
3 7 6 3
4 1 7 5
(2 )
(2 )
x y
x y

 

9
2 21
x 18
y
20
2 5
x 35
y
 9
2
20
2
21
x 5
x
18
y
35
y

11
2
26
x
17
y