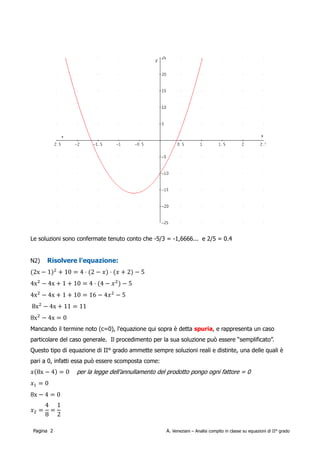
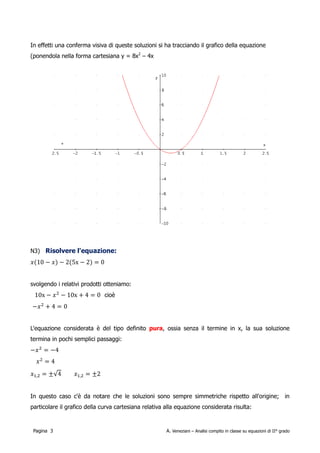
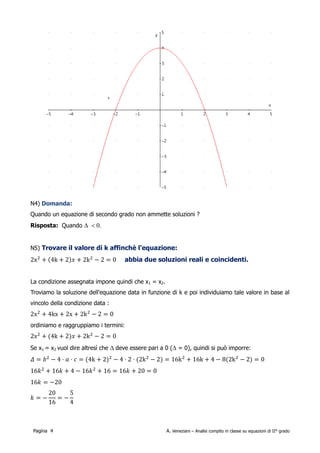
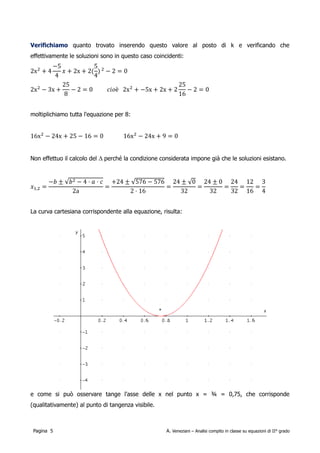
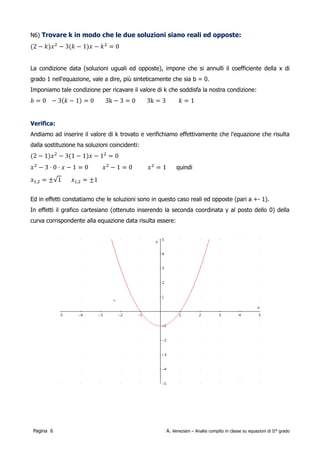
Il documento analizza il compito in classe di matematica riguardante le equazioni di secondo grado, illustrando vari esempi di risoluzione e condizioni per le soluzioni reali. Viene discussa la determinazione del discriminante e la possibilità di ottenere soluzioni coincidenti o opposte in base ai parametri dell'equazione. In aggiunta, si menzionano conferme visive attraverso grafici delle equazioni trattate.

1. Matematica – dalla lezione del 27-1-2011 del prof. L.G. Cancelliere
Classe 2E
Svolgimento esercizi assegnati nel compito in classe del 24/1/2011:
Risolvere l'equazione:
19
3x 2=2− x
5
Per prima cosa si porta tutti a sinistra gli addendi che formano l'espressione:
19
3x 2 x−2=0
5
Eliminiamo poi il coefficiente frazionario moltiplicando per 5 tutta l'equazione (ovviamente a destra
il risultato di tale operazione da ancora 0 in quanto 5 x 0 = 0)
19
5⋅3x 25⋅ x−5⋅2 = 15 x 219 x−10 = 0
5
Successivamente ci si chiede se l'equazione abbia effettivamente soluzioni (reali), e per far ciò
calcolo il ∆:
=b 2−4⋅a⋅c=192−4⋅15⋅−10=361−600=961  0
allora risulta quindi che le soluzioni reali esistono e sono distinte (caso ∆ > 0).
Andiamo allora a calcolarle tramite la classica formula risolutiva per le equazioni di II° grado:
−b±  −b±  b 2−4⋅a⋅c −19± 19 −4⋅15⋅−10
2
x 1,2= = = =¿
2a 2a 2⋅15
−19± 961 −19±31 −1931 12 4 2
x 1,2= = x 1= = = =
30 30 30 30 10 5
−19−31 50 5
x 2= = =
30 30 3
Queste soluzioni possono essere indirettamente confermate cercando di plottare l'equazione con
uno strumento quale Derive; risulta il grafico qui a seguire:
Pagina 1 A. Veneziani – Analisi compito in classe su equazioni di II° grado

2. Le soluzioni sono confermate tenuto conto che -5/3 = -1,6666... e 2/5 = 0.4
Risolvere l'equazione:
2x−1210=4⋅2−x⋅ x2−5

4x 2−4x110=4⋅ 4−x 2−5
4x 2−4x110=16−4 x 2−5
8x 2−4x11=11 8x 2−4x=0
Mancando il termine in x, l'equazione qui sopra è detta pura, e rappresenta un caso particolare del
caso generale. Il procedimento per la sua soluzione può essere “semplificato”.
Questo tipo di equazione di II° grado x 1=0 ammette sempre soluzioni reali e distinte, una delle
quali è pari a 0, infatti essa può essere scomposta come:
x 8x−4=0
4 1
8x−4=0 x 2= =
8 2
In effetti una conferma visiva di queste soluzioni si ha tracciando il grafico della equazione
Pagina 2 A. Veneziani – Analisi compito in classe su equazioni di II° grado

3. (ponendola nella forma cartesiana y = 8x2 – 4x):
Risolvere l'equazione:
x 10− x−25x−2=0
svolgendo i relativi prodotti otteniamo:
10x− x 2−10x 4=0 −x 24=0
L'equazione considerata è del tipo definito spuria, ossia senza il termine in x, la sua soluzione
termina in pochi semplici passaggi:
−x 2=−4 x 2=4 x 1,2=± 4=±2
In questo caso c'è da notare che le soluzioni sono sempre simmetriche rispetto all'origine; in
particolare il grafico della curva cartesiana relativa alla equazione considerata risulta:
Pagina 3 A. Veneziani – Analisi compito in classe su equazioni di II° grado

4. Domanda: Quando un equazione di secondo grado non ammette soluzioni ?
Risposta: Quando ∆ < 0.
Trovare il valore di k affinchè l'equazione:
2x 24k2 x2k 2−2=0
abbia due soluzioni reali e coincidenti.
La condizione assegnata impone quindi che x1 = x2.
Troviamo la soluzione dell'equazione data in funzione di k e poi individuiamo tale valore in base al
vincolo della condizione data :
2x 24kx2x2k 2−2=0
ordiniamo e raggruppiamo i termini:
2x 24k2 x2k 2−2=0
Se x1 = x2 vuol dire altresì che ∆ deve essere pari a 0 (∆ = 0), quindi si può imporre:
=b 2−4⋅a⋅c=4k22−4⋅2⋅2k 2−2=16k 216k4−82k 2 −2=0
16 k 216 k 4−16 k 216=16 k20=0
16 k =−20 20 5
k=− =−
16 4
Verifichiamo quanto trovato inserendo questo valore al posto di k e verificando che effettivamente
Pagina 4 A. Veneziani – Analisi compito in classe su equazioni di II° grado

5. le soluzioni sono in questo caso coincidenti:
2
2x 42−5
4  
x2x2
5
4
−2=0 
2
2x −5x2x2  
25
16
−2=0
25 moltiplichiamo tutta l'equazione per 8:
2x 2−3x −2=0
8
16x 2−24x25−16=0 16x 2−24x9=0
Non effettuo il calcolo del ∆ perché la condizione considerata impone già che le soluzioni esistano.
−b± b 2−4⋅a⋅c 24±  576−576 24±  0 24±0 24 12 3
x 1,2= = = = = = =
2a 2⋅16 32 32 32 16 4
La curva cartesiana corrispondente alla equazione, risulta:
e come si può osservare tange l'asse delle x nel punto x = ¾ = 0,75, che corrisponde
(qualitativamente) al punto di tangenza visibile.
Pagina 5 A. Veneziani – Analisi compito in classe su equazioni di II° grado

6. Trovare k in modo che le due soluzioni siano reali ed opposte:
2−k  x 2−3 k−1 x−k 2=0
La condizione data (soluzioni uguali ed opposte), impone che si annulli il coefficiente di grado 1
(ossia della x) nell'equazione, vale a dire, più sinteticamente che sia b = 0.
Imponiamo tale condizione per ricavare il valore di k che soddisfa la nostra condizione:
b=0=3k −1 3k−3=0 3k=3 k=1
Andiamo ad inserire il valore di k trovato e verifichiamo effettivamente che l'equazione che risulta
dalla sostituzione ha soluzioni coincidenti:
2−1 x 2−31−1 x−1 2=0 x 2−3⋅0⋅x−1=0
x 2−1=0 x 2=1 x 1,2=± 1=±1
Ed in effetti constatiamo che le soluzioni sono in questo caso reali ed opposte (pari a +- 1).
In effetti il grafico cartesiano (ottenuto inserendo la seconda coordinata y al posto dello 0) della
curva corrispondente alla equazione data risulta essere:
Pagina 6 A. Veneziani – Analisi compito in classe su equazioni di II° grado