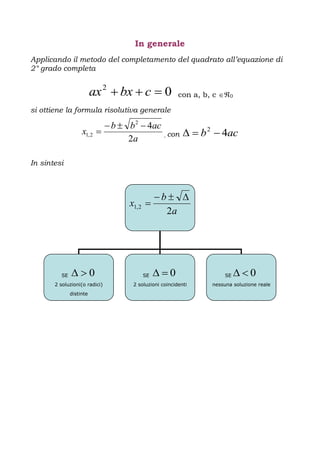
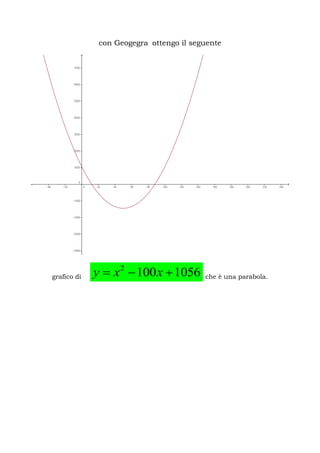
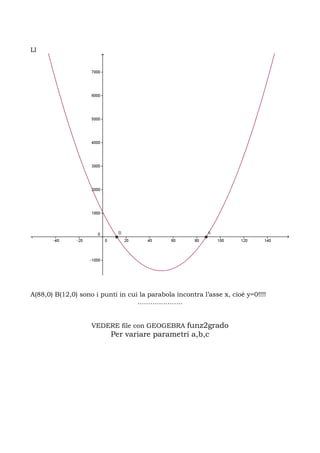
Il documento tratta la risoluzione delle equazioni di 2° grado, presentando l'equazione x^2 - 100x + 1056 = 0. Vengono descritti due metodi per risolverla: la scomposizione in fattori e il completamento del quadrato, trovando le soluzioni x1=12 e x2=88, con solo x=12 valida nel contesto specificato. Infine, viene definita la funzione associata e menzionato un grafico della parabola tramite Geogebra.

1. Equazioni di 2° grado
PROBLEMA
(Es. es. 457 pag. 841 vol. 2 Zanichelli biennio)
…… siamo giunti all’equazione di 2° grado
x 2  100 x  1056  0 con 0  x  75
Come risolvere le equazioni di 2° grado
Metodo 1
Scomposizione in fattori e legge di annullamento del prodotto
x 2  100 x  1056  x  12x  88
x 12  x  88  0
X1=12 X2=88
Metodo 2
Completamento del quadrato
x 2  100 x  1056  0
si può scrivere come
x  502  1444
da cui …….
X1=12 e X2=88

2. In generale
Applicando il metodo del completamento del quadrato all’equazione di
2° grado completa
ax 2  bx  c  0 con a, b, c 0
si ottiene la formula risolutiva generale
 b  b 2  4ac
x1, 2  , con   b
2
 4ac
2a
In sintesi
b 
x1, 2 
2a
SE 0 SE 0 SE 0
2 soluzioni(o radici) 2 soluzioni coincidenti nessuna soluzione reale
distinte

3. Casi particolari
(da completare)

4. Dall’equazione di 2° grado alla funzione di 2° grado
Per risolvere il problema (es. 457 pag. 841 vol. 2 Zanichelli biennio)
siamo giunti all’equazione di 2° grado
x 2  100 x  1056  0 con 0  x  75
Delle due soluzioni ( o radici) trovate x1=12 e x2=88
Per le C.E. x2=88 non è accettabile, pertanto il problema ammette una
soluzione x=12.
Definisco ora la funzione di 2° grado associata …
f :x  y
y  x 2  100 x  1056 , con x 
oppure
f ( x)  x 2  100 x  1056
e la rappresento graficamente ….

5. con Geogegra ottengo il seguente
grafico di y  x 2  100 x  1056 che è una parabola.

6. Ll
A(88,0) B(12,0) sono i punti in cui la parabola incontra l’asse x, cioè y=0!!!!
…………………
VEDERE file con GEOGEBRA funz2grado
Per variare parametri a,b,c