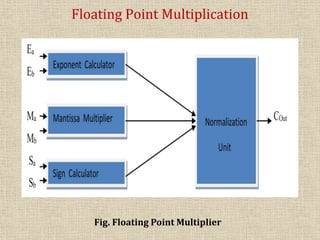
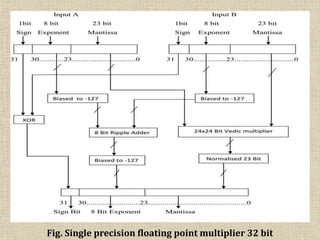
This seminar report summarizes the design and implementation of a floating point multiplier using Vedic multiplication techniques on an FPGA. It describes the key components of a floating point multiplier, reviews existing multiplication algorithms, and introduces the ancient Vedic multiplication method. The report outlines the design of a proposed 32-bit floating point Vedic multiplier, including mantissa, exponent, and sign calculation units. Experimental results show the Vedic multiplier utilizes 9% of slices on the target FPGA and has a maximum delay of 18.872ns, demonstrating its advantages over other multipliers in terms of speed and area efficiency.

1. A
Seminar Report On
“FPGA Implementation of Vedic Floating Point
Multiplier”
By
Mr. Bhushan Sunil Mhaske.
2016MVE006
1St Year M-Tech ES&VLSI Design
Under The Guidance of
Prof. Y.V.JOSHI
Dept. of Electronics and Telecommunication Engineering
Shri Guru Gobind Singhji Institute of Engineering and Technology,
Nanded -431606 (MS)

2. Flow of the presentation…
Introduction
Literature Review
Floating Point Multiplication
An Overview of Vedic Multiplication
Algorithms for Vedic Multiplication
Experimental Result & Verification
conclusion
References

3. INTRODUCTION
Most of the scientific operation involve floating point computations.
Fixed point and floating point number representations are being
widely used by various applications in the design of (DSPs).
Dynamic range and precision considerations determine whether fixed
point or floating point representations are to be used.
Among various floating point arithmetic operations, multiplication is
more frequently used in many applications.
As multipliers play a critical role in any digital design, It is necessary
to implement faster multipliers occupying less area and consuming
less power.
facilitates optimized utilization of resources & minimum time delay.

4. LITERATURE REVIEW
 The floating point numbers in binary number system are represented
in two formats namely, IEEE 754 single and double precision.
 These formats are characterized by exponent, mantissa and sign fields.
 i)Single Precision Representation (32 bit)
 ii) Double precision Representation (64 bit)
Mantissa 52 bit
(LSB)
Exponent 11 bitSign1 bit
(MSB)
Sign1 bit
(MSB)
Exponent 8 bit Mantissa 23 bit
(LSB)

5.  Floating point multiplication utilizes a 24- bit and 53- bit multiplier
for multiplication of its significand in single precision and double
precision respectively.
 Different multiplication algorithms are used for multiplying the
significand likewise Booths & Add Shift Technique.
 Array multiplier, redundant binary structures & tree structures
also used but they have problem of larger delay.
 Floating point multiplication can also be done by using pipelining
method wherein addition of exponents, multiplication of
significands and calculation of sign bit can be done in parallel.
 In this we introduced an algorithm using ancient Vedic
mathematics rules for fast multiplication which generate partial
products concurrently.
Contd....

6. Floating Point Multiplication
Fig. Floating Point Multiplier

7.  Multiplication of two floating point number is done by multiplying
the normalized 24 bit mantissa.
 The exponents of both the operands are added to obtain the
product exponent.
 To obtain biased exponent the resultant sum is subtracted from
127 in case of single precision and 1023 in case of double
precision.
 The addition operation involves the use of 8- bit and 11- bit ripple
carry adder for single and double precisions respectively.
 for the sign calculation the input sign bits are XORed.
Contd....

8. An Overview of Vedic Multiplication
 The Vedic multiplication system is based on 16 Vedic sutras which
describes natural ways of solving a whole range of mathematical
problems.
 Out of these 16 Vedic Sutras the Urdhva-triyakbhyam sutra is general
multiplication formula applicable to all cases. it literally means
vertically & crosswise.
Fig.The Vedic Multiplication Method

9.  Consider the numbers A and B where A = a2a1a0 and B = b2b1b0. The
LSB of A is multiplied with the LSB of B: s0=a0b0; Then a0 is
multiplied with b1, and b0 is multiplied with a1 and the results are
added together as: c1s1=a1b0+a0b1;
 Here c1 is carry and s1 is sum. Next step is to add c1 with the
multiplication results of a0 with b2, a1 with b1 and a2 with
b0.c2s2=c1+a2b0+a1b1 + a0b2;
 Next step is to add c2 with the multiplication results of a1 with b2 and
a2 with b1.
c3s3=c2+a1b2+a2b1;
Similarly the last step
c4s4=c3+a2b2;
Now the final result of multiplication of A and B is c4s4s3s2s1s0.
 In this method the partial products are generated simultaneously
which itself reduces delay and makes this method fast.
Contd....

10. PROPOSED DESIGN
 The proposed multiplier for floating point numbers can divided in
four different units:
1. Mantissa Calculation unit
2. Exponent calculation unit
3. Sign calculation unit
4.Control unit
 Mantissa calculation unit requires a 24 bit multiplier.
 Exponent calculation unit is implemented by using 8 bit ripple
carry adder .
 The advantage of ripple carry adder is its low area and simple
layout.

11. Algorithm Steps
1. Multiplying the significand (1.M1*1.M2 )
2. Placing the decimal point in the result .
3. Adding the exponents i.e.,(E1 + E2 – Bias)
4. Obtaining the sign; i.e. s1 XOR s2
5. Normalizing the result; i.e. obtaining 1 at the MSB of the result’s
significand.
6. Checking for underflow/overflow occurrence .

12. Fig. Single precision floating point multiplier 32 bit

13.  Mantissa multiplication is done with 24 bit vedic multiplier.
 Mantissa is expressed in 23 bit which is normalized by adding 1 at
MSB.
 Since the inputs are normalized number then the intermediate
product has the ‘Leading 1’ at bit 46 or 47 .
 If the leading one is at bit 46 (i.e. to the left of the decimal point)
then the intermediate product is already a normalized number and
no shift is needed.
 If the leading one is at bit 47 then the intermediate product is
shifted to the right and the exponent is incremented by 1.
 The shift operation is done using combinational shift logic made by
multiplexers.
Contd....

14. Fig. Block Diagram of 24*24 Bit Vedic Multiplier
24*24 Bit Vedic Multiplier

15. Block Diagram Explanation
 A 24*24 Vedic multiplier is design by using four 12*12 Vedic
multipliers based urdhva Triyakbhyam.
 It requires four 12x12 BIT multipliers and two 36 BIT ripple carry
adders and one 24 BIT ripple carry adders.
 Here first block 12X12 multiplier consists of lower 12 bits of x i.e.
x(11 down to 0) and y(11 down to 0),
 second block 12*12 Vedic multiplier inputs are x(23 down to 12)
and y(11 down to 0) .
 out off 24 bit output of first block lower 12 bits are separated and
higher order bits are appended as 12 lower bits in front
augmented with “000000000000” (12 zeroes).

16. Contd...
 Higher order 12 bit of y(23 down to 12) and lower order 12 bits of
x i.e. x(11 down to 0) are multiplied and appended in-front with
“000000000000”(MSB) to make 36 bit data .
 similarly both higher order 12 bits of x and y i.e. x(23 down to 12)
and y(23 down to 12) are multiplied and 36 bit data is formed by
appending “000000000000”(LSB).
 Resultant of 24*24 bit multiplier is 48 bits consists of 36 higher
bits from 36 bit adder output and lower order 12 bits 36+12=48
bits.

17. Experimental Result & Verification
 We implement the 32 bit Vedic multiplier in Xilinx with xc5vlx50t-
2ff1136 as targeted device and we found the following
experimental results:
RTL Schematic

18. Maximum combinational path delay: 18.872ns
Number of occupied Slices: 676 out of 7,200
Utilization factor = 9%

19. Conclusion
 Vedic multiplier is faster than array multiplier and Booth
multiplier.
 As the number of bits increases from 8x8 bits to 16x16 bits, the
timing delay is greatly reduced for Vedic multiplier as compared to
other multipliers.
 Vedic multiplier has the greatest advantage as compared to other
multipliers over gate delays and regularity of structures.

20. Reference
1. IEEE 754-2008, IEEE Standard for Floating-Point Arithmetic.
2. Brian Hickmann, Andrew Krioukov, and Michael Schulte, Mark
Erle, ”A Parallel IEEE 754 Decimal Floating-Point Multiplier,” In
25th International Conference on Computer Design ICCD, Oct.
2007.
3. Kavita Khare, R.P.Singh, NilayKhare,”Comparison of pipelined
IEEE- 754 standard floating point multiplier with npipelined
multiplier”.
4. verilog-code.blogspot.com
5. www.vedicmaths.com

21. Thank You…!!!
“My amount is little, but my efforts are sincere.”