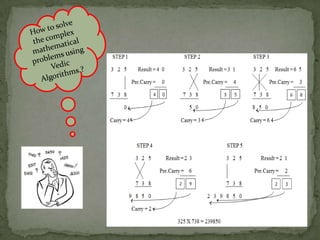
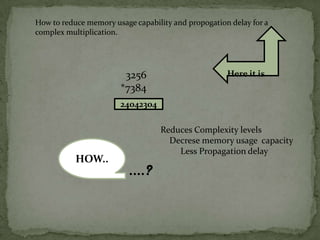
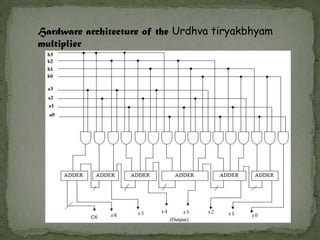
The document discusses different methods for multiplication and their associated delays. It introduces the concept of Vedic mathematics as an ancient methodology for calculations based on 16 formulas. It then describes the Urdhva Tiryakbhyam multiplier technique, which reduces complexity, memory usage, and propagation delay for multiplication by calculating partial products in parallel rather than sequentially. This technique can be implemented in hardware to create an efficient complex multiplier with improved speed and lower power consumption compared to other architectures.

1. Presented by..
S.Noor Mohammad

4. Vedic
Mathematics

5. The delay associated with the array multiplier is the
Array
time taken by the signals to propagate through the
Multiplier
gates that form the multiplication array.
Large booth arrays are required for high speed
multiplication and exponential operations which in
turn require large partial sum and partial carry
Booth registers.
Multiplier
Multiplication of two n-bit operands using a radix-4
booth recording multiplier requires approximately n
/ (2m) clock cycles to generate the least significant
half of the final product, where m is the number of
Booth recorder adder stages. Thus, a large
propagation delay is associated with this case.

6. What is Vedic Mathematics..?
The word „Vedic‟ is derived from the word „veda‟
which means the store-house of all knowledge.
Jagadguru Shankaracharya Bharati Krishna Teerthaji
Maharaja (1884-1960)
Vedic Mathematics is the ancient methodology of
Indian mathematics which has a unique technique of
calculations based on 16 Sutras (Formulae).
It covers explanation of several modern mathematical
terms including arithmetic, geometry (plane, co-
ordinate), trigonometry, quadratic
equations, factorization and even calculus.

7. 16 Suthras(Formules) in Vedic Mathematics
1) (Anurupye) Shunyamanyat
2) Chalana-Kalanabyham
3) Ekadhikina Purvena
4) Ekanyunena Purvena
5) Gunakasamuchyah
16) Yaavadunam 6) Gunitasamuchyah
15) Vyashtisamanstih 7)Nikhilam Navatashcaramam
14) Urdhva-tiryakbhyam Dashatah
13) Sopaantyadvayamantyam 8) Paraavartya Yojayet
12) Shunyam Saamyasamuccaye 9) Puranapuranabyham
11) Shesanyankena Charamena 10) Sankalana- vyavakalanabhyam

9. Conventional method for 4-bit
multiplication.
3256*7384
3256
*7384
13024 Memory usage is high
for each stage
26048+ and causes delay in
9768++ execution
22792+++
24042304

10. How to reduce memory usage capability and propogation delay for a
complex multiplication.
3256 Here it is
*7384
24042304
Reduces Complexity levels
Decrese memory usage capacity
Less Propagation delay
HOW..
….?

11. 1. CP X0 = X0 * Y0 = A
Y0
2. CP X1 X0 = X1 * Y0+X0 * Y1 = B
Y1 Y0
3. CP X2 X1 X0 = X2 * Y0 +X0 * Y2 +X1 * Y1 = C
Y2 Y1 Y0
4. CP X3 X2 X1 X0 = X3 * Y0 +X0 * Y3+X2 * Y1 +X1 *Y2 = D
Y3 Y2 Y1 Y0
5. CP X3 X2 X1 = X3 * Y1+X1 * Y3+X2 * Y2 = E
Y3 Y2 Y1
6. CP X3 X2 = X3 * Y2+X2 * Y3 = F
Y3 Y2
7 CP X3 = X3 * Y3 = G
Y3

12. Hardware architecture of the Urdhva tiryakbhyam
multiplier

13. Where it can be used
Basic Applications: Vedic Mathematics is a branch of
Mathematics which teaches pattern-observation and
faster calculations.
Vedic Mathematics covers Arithmatics
Decimal operations in all decimal work,
Ratios, Proportions,
Trigonometry, Percentages,
Averages, Interest, Annuities,
Discount, the Centre of Gravity of Hemispheres,
Transformation of Equations, Dynamics,
Statistics, Hydro Statistics,
Pneumatics, Applied Mechanics,
Solid Geometry, Plane Spherical
Trigonometry, Astronomy, etc.
ASCI Application: The propagation delay of the resulting
(16, 16)x(16, 16) complex multiplier is only 4ns and
consume 6.5 mW power. We achieved almost 25%
improvement in speed from earlier reported complex
multipliers, e.g. parallel adder and DA based architectures.