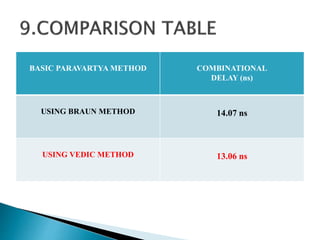
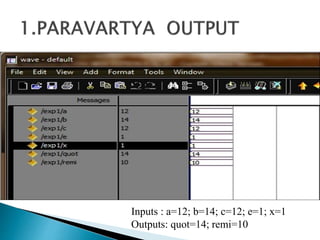
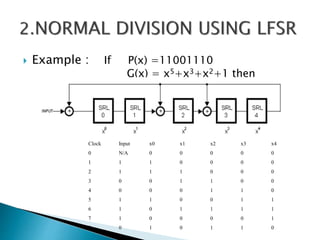
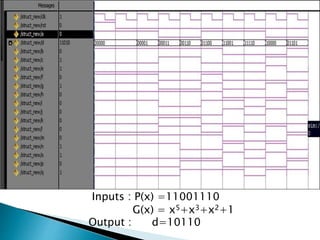
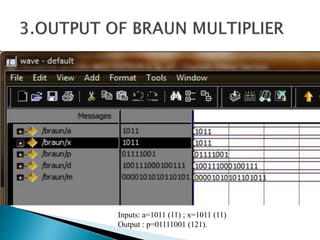
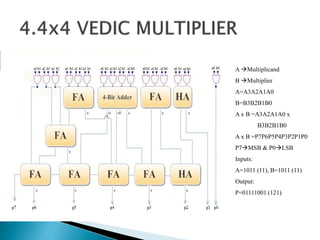
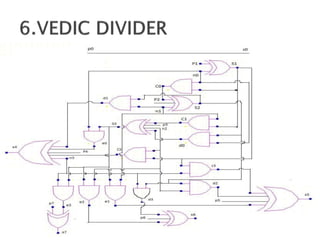
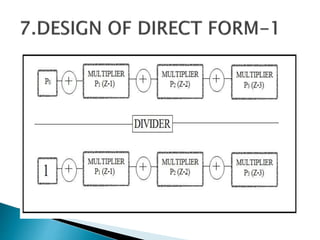
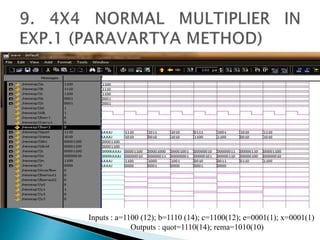
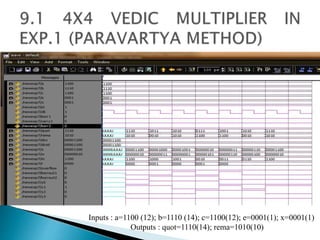
1) The document presents the design of arithmetic operations using Vedic mathematics to improve parameters like combinational delay, number of slices, flip flops, and LUTs compared to conventional methods. 2) It describes the Vedic mathematics techniques of Paravartya and Urdhva Tiryagbhyam and shows their implementation in 4x4 multipliers and dividers in VHDL with improvements in delay and resource usage. 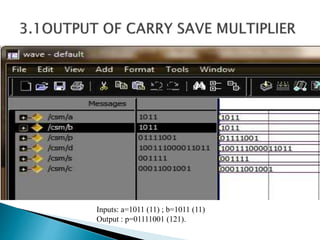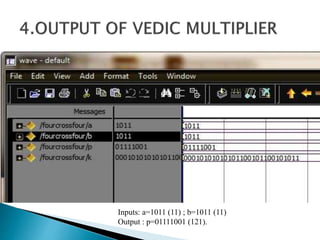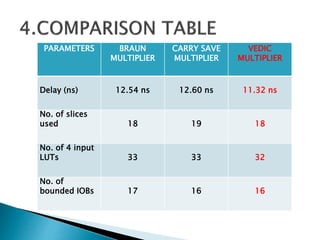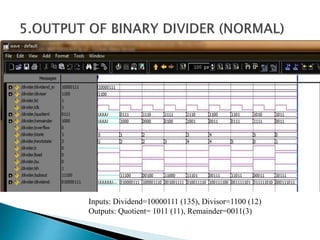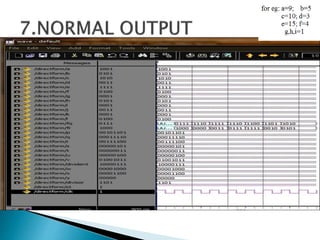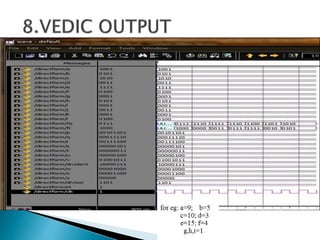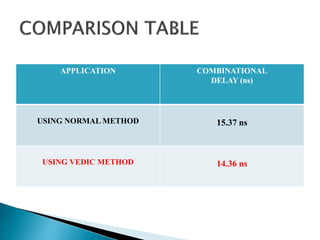3) The experiments show that the Vedic multiplier and divider have lower delay and use fewer resources than conventional designs, with the Paravartya method also improving speed in applications like polynomial division.

1. PRESENTED BY GUIDED BY
BINU SIVA SINGH S K Mr. KISHOR SONTI
REG NO:3182105 ASSISTANT PROFESSOR
MTECH VLSI DESIGN

2. To design architecture for ARITHEMATIC
OPERATIONS using VEDIC MATHEMATICS and
to improve the parameters in terms of
combinational delay, No. of slices, No. of slice
Flip Flops, No. of bounded IOBs, No. of 4
input LUTs.

3.  Vedic Mathematics ?
Because it was originated by Vedas (Atharva Vedas) and with
the help of sixteen sutras and sub sutras it was reintroduced by
Swami Krishna tirtha ji
 How it is differ from Conventional Mathematics?
Number of steps is getting reduced while compared to
normal Mathematics as a result VLSI basics parameters area
power and speed are improved
 This is so because the Vedic formulae are claimed to be based on
the natural principles on which the human mind works
 Vedic Mathematics is a methodology of arithmetic rules that
allow more efficient speed implementation
 It also provides some effective algorithms which can be applied
to various branches of engineering such as computing.

4. 1.Basic PARAVARTYA METHOD
2.Normal division using LFSR
3.4x4 Multiplier (Braun,CSM)
4.4x4 Vedic Multiplier
Comparison Table
5.Binary Divider (Normal)
6.Binary Divider (Vedic)
Comparison Table
7.Application : Faster form Realization (Normal
Multiplier)
8. Application : Faster form Realization
(Paravartya Method)

5. 9.4x4 Vedic Multiplier in exp.1(PARAVARTYA
METHOD)
10.4x4 Vedic Multiplier in exp.7
11.4x4 Vedic Multiplier in exp.8
12.Compare exp 10 & 11
13.Compare exp 1 & 9

7.  TOOLSET : XILINX 12.1
: MODELSIM 6.3
 LANGUAGE : VHDL

8.  ‘Paravartya’ method of Vedic mathematics is
useful for polynomial division of any order
 “Paravartya Yojayet” or “transpose and apply”
is an advanced form of Remainder theorem or
Horner’s synthetic division process
 Advantage
- hardware utilization and timing
optimization as compared to other methods

10. Inputs : a=12; b=14; c=12; e=1; x=1
Outputs: quot=14; remi=10

11.  Example : If P(x) =11001110
G(x) = x5+x3+x2+1 then
Clock Input x0 x1 x2 x3 x4
0 N/A 0 0 0 0 0
1 1 1 0 0 0 0
2 1 1 1 0 0 0
3 0 0 1 1 0 0
4 0 0 0 1 1 0
5 1 1 0 0 1 1
6 1 0 1 1 1 1
7 1 0 0 0 0 1
8 0 1 0 1 1 0

12. Inputs : P(x) =11001110
G(x) = x5+x3+x2+1
Output : d=10110

13.  Braun Multiplier is the simple parallel Multiplier
 Array consists of (n-1) rows of carry save adder, in which
each row contains (n-1) full adder cells and n2 number of and
gate for the given n numbers of inputs
 The last row is the Ripple Carry Adder for carry propagation

14. A Multiplicand
X Multiplier
A=A3A2A1A0
X=X3X2X1X0
A x X =A3A2A1A0 x X3X2X1X0
A x X =P7P6P5P4P3P2P1P0
P7MSB & P0LSB
Inputs:
A=1011 (11), X=1011 (11)
Output:
P=01111001 (121)

15. Inputs: a=1011 (11) ; x=1011 (11)
Output : p=01111001 (121).

16.  Carry save multiplier has three main stages
1. The first stage is an array of half adders
2. The middle stages are arrays of full adders
3. The last stage is an array of ripple carry adders .This
stage is called the vector merging stage

17. A Multiplicand
B Multiplier
A=A3A2A1A0
B=B3B2B1B0
A x B =A3A2A1A0 x B3B2B1B0
A x B =P7P6P5P4P3P2P1P0
P7MSB & P0LSB
Inputs:
A=1011 (11), B=1011 (11)
Output:
P=01111001 (121)

18. Inputs: a=1011 (11) ; b=1011 (11)
Output : p=01111001 (121).

19. It has a glitching problem which is due
to the Ripple Carry Adder in the last stage
of the design

20.  Vedic multiplier is based on Urdhya Tiragbhyam. This Sutra
have been used for the multiplication of two binary numbers
 Designed by using a new 4-bit adder and implemented in
HDL language
 Advantage:
Hardware utilization
Delay is reduced as compared to other multipliers

21. This method consider
two four digit binary
numbers by urdhva
tiryakbhyam as shown
in the figure. The digits
of the both side of the
line are multiplied and
added with the carry
from the initial step.
Initially carry is taken to
be zero.

22. Inputs: a=1011 (11) ; b=1011 (11)
Output : p=01111001 (121).

23.  4-bit adder performs the function of 4-bit addition that
gives a sum and two bits of carry as output
 A,B,C,D are four inputs; C0 and C1 are LSB and MSB of
carry outputs respectively and Sum is the sum of four
inputs
The Boolean expressions for the same are given below

25. Inputs: a=‘1’; b=‘1’;c=‘1’; d=‘1’
Outputs: sum=‘0’; ca=‘0’; cb=‘1’

26. A Multiplicand
B Multiplier
A=A3A2A1A0
B=B3B2B1B0
A x B =A3A2A1A0 x
B3B2B1B0
A x B =P7P6P5P4P3P2P1P0
P7MSB & P0LSB
Inputs:
A=1011 (11), B=1011 (11)
Output:
P=01111001 (121)

27. Inputs: a=1011 (11) ; b=1011 (11)
Output : p=01111001 (121).

28. PARAMETERS BRAUN
MULTIPLIER
CARRY SAVE
MULTIPLIER
VEDIC
MULTIPLIER
Delay (ns) 12.54 ns 12.60 ns 11.32 ns
No. of slices
used 18 19 18
No. of 4 input
LUTs 33 33 32
No. of
bounded IOBs 17 16 16

29.  By Comparing method (3,3.1 & 4) ,I conclude
that compare to normal multiplier vedic
multiplier is more effective by reducing the
delay and number of slices

30.  Design of parallel divider for positive
numbers
 For eg. 8 bit Dividend and 4 bit Divisor to
obtain 4 bit quotient
 Binary multiplication can be carried out as a
series of add and shift operations
 Division can be carried out by a series of
subtraction and shift operations.

31. Inputs: Dividend=10000111 (135), Divisor=1100 (12)
Outputs: Quotient= 1011 (11), Remainder=0011(3)

32.  Design of parallel divider for positive numbers
For eg. 8 bit Dividend and 4 bit Divisor to obtain
4 bit quotient
Consider a dividend polynomial
 p(x)=x7+x6+x4+x+1 and divisor polynomial
m(x)= x4+x+1.
 Writing divisor in terms of binary coefficients and
neglecting the highest power
 n(x) = 0x3+0x2+x+1
 c(x) = sn-1 * (n(x)) = 1 * {0,0,1,1} = {0,0,1,1}
 d(x) = sn-2 * (n(x)) = 0 * {0,0,1,1} = {0,0,0,0}
 e(x) = sn-3 * (n(x)) = 0 * {0,0,1,1} = {0,0,0,0}

35. Inputs : p= 11010011, n=10011
Outputs :Quotient=1100, Remainder=0111.

36. PARAMETERS NORMAL DIVIDER VEDIC DIVIDER
Delay (ns) 8.6 ns 8.2 ns
No. of slices used 17 7
No. of 4 input LUTs 31 12
No. of bounded IOBs 23 20

37.  Faster form Realization
-Direct Form I Realization
-Direct Form II Realization
-Cascade Form Realization
-Parallel Form Realization

38.  Consider the equation as
ax(n-1)+bx(n-2)+cx(n-3)
1+dx(n-1)+ex(n-2)+fx(n-3)

39.  The design of Direct Form as follows
NORMAL METHOD VEDIC METHOD
4 bit Adder 4 bit Adder
Normal Multiplier Vedic Multiplier
Normal Divider Vedic Divider

43. APPLICATION COMBINATIONAL
DELAY (ns)
USING NORMAL METHOD 15.37 ns
USING VEDIC METHOD 14.36 ns

44.  By Comparing method (5 & 8) ,I conclude that
compare to normal method, vedic method is
more effective by reducing the delay and
number of slices

45. Inputs : a=1100 (12); b=1110 (14); c=1100(12); e=0001(1); x=0001(1)
Outputs : quot=1110(14); rema=1010(10)

46. Inputs : a=1100 (12); b=1110 (14); c=1100(12); e=0001(1); x=0001(1)
Outputs : quot=1110(14); rema=1010(10)

47. BASIC PARAVARTYA METHOD COMBINATIONAL
DELAY (ns)
USING BRAUN METHOD 14.07 ns
USING VEDIC METHOD 13.06 ns

48.  Harpreet Singh Dhillon and Abhijit Mitra, “A Reduced– Bit Multipliction
Algorithm for Digital Arithmatics”, International Journal of Computational
and Mathematical Sciences 2.2 @ www.waset.orgSpring2008
 Parth Mehta, Dhanashri Gawali, “Conventional versus Vedic mathematics
method for Hardware implementation of a multiplier”, International
conference on Advance in Computing, Control, and Telecommunication
Technologies, 2009
 Sumita Vaidya and Deepak Dandekar, “Delay-Power Performance
comparison of Multipliers in VLSI Circuit Design”, International Journal of
Computer Networks & Communications (IJCNC), Vol.2, No.4, July 2010.
 S.S.Kerur, Prakash Narchi, Jayashree C N, Sabari Harish M Kittur and
Girish V A “Implementation of Vedic Multiplier For Digital Signal
Processing” International conference on VLSI communication &
instrumentation (ICVCI) 2011

49.  Jagadguru Swami Sri Bharat Krsna Thirthaji Maharaja “Vedic
Mathematics” , Motialal Banarsidass Publishers Pvt. Ltd, Delhi,
India
 M. Morris Mano, “Digital Logic and Computer Design” Prentice,
Hall of India Pvt. Ltd, New Delhi, India
 Samir Palnitkar, “Verilog HDL –A guide to Digital Design and
Synthesis”, Pearson Education., New Delhi, India
 Tomas Henriksson and Dake Liu, “Implementation of Fast CRC
Algorithm”, Dept. Of Electrical Engineering, Linkopings
Universitet, Sweden
 Azaleah Amina P. Chio, Jonathan A. Sahagun, and Delfin Jay M.
Sabido IX, “VLSI Implementation Of a (255, 223) Reed-Solomon
Error-Correction Codec”, Advanced Science and Technology
Institute, Department of Science and Technology, Proceedings of
2nd National ECE Conference