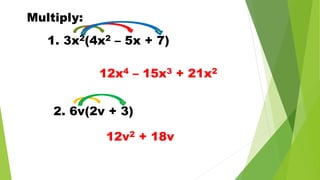
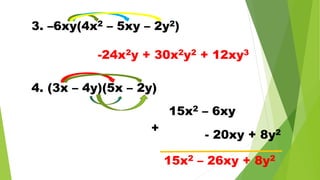
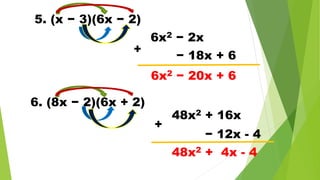
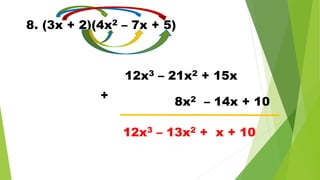
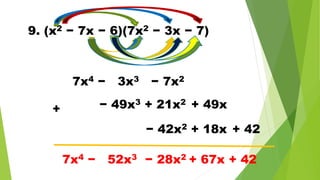
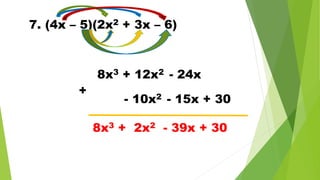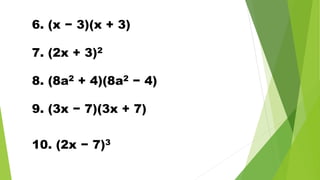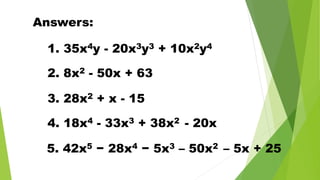The document discusses multiplying polynomials, including multiplying monomials, combining like terms, and special cases such as the sum and difference of binomials, squares of binomials, and cubes of binomials. Examples are provided for multiplying polynomials with 2, 3, or 4 terms. Formulas and step-by-step workings are shown for finding products of binomial expressions.

1. Multiplication of
Polynomials

2. 1. -t4 + 5t3 + 3t2 - 16
Answer to the assignment:
2. 5x + 2y - 6

3. Review:
Multiply the following monomials:
(3)(4x) = 12x
(5x3 y2)(2x3y) =
(y3)(-y3) =
(3x2)(4xy3) =
(6xy4)(2x3y3) =
(-x4y3)(-x3y3) =
(2xy5)(-8x3y) =
(7xy4)(2x3y3) =
10x6y3
-y6
12x3y3
12x4y7
x7y6
-16x4y6
14x4y7

4. Combine like terms (if you can).
Distribute each term of the first
polynomial to every term of the second
polynomial.
Remember that when you multiply two
terms together you must multiply the
coefficient (numbers) and add the
exponents.

5. Multiply:
1. 3x2(4x2 – 5x + 7)
12x4 – 15x3 + 21x2
2. 6v(2v + 3)
12v2 + 18v

6. 3. –6xy(4x2 – 5xy – 2y2)
-24x2y + 30x2y2 + 12xy3
4. (3x – 4y)(5x – 2y)
15x2 – 6xy
- 20xy + 8y2
15x2 – 26xy + 8y2
+

7. 5. (x − 3)(6x − 2)
6x2 − 2x
− 18x + 6
+
6x2 − 20x + 6
6. (8x − 2)(6x + 2)
48x2 + 16x
+
− 12x - 4
48x2 + 4x - 4

8. 7. (4x – 5)(2x2 + 3x – 6)
8x3 + 12x2 - 24x
- 10x2 - 15x + 30
+
8x3 + 2x2 - 39x + 30

9. 8. (3x + 2)(4x2 – 7x + 5)
12x3 – 21x2 + 15x
8x2 – 14x + 10
+
12x3 – 13x2 + x + 10

10. 9. (x2 − 7x − 6)(7x2 − 3x − 7)
7x4 − 3x3 − 7x2
− 49x3 + 21x2 + 49x
− 42x2 + 18x + 42
+
7x4 − 52x3 − 28x2 + 67x + 42

11. Special Products:
Sum and Difference of Two Binomials
1. (x + 5)(x − 5) 1. x2 - 25
(a)2 – (b) 2
2. (x - 8)(x + 8) 2. x2 - 64
3. (x – 2y)(x + 2y) 3. x2 – 4y2
(a – b)(a+b) =

12. Squares of Two Binomials
(a+b)2 = (a + b)(a + b) = (a)2 ± 2(a)(b) +(b)2
1. (x − 1)2 = (x)2 ± 2(x)(1) +(1)2
= x2 + 2x + 1
2. (x − 6)(x – 6)2 = (x − 6)2
= (x)2 - 2(x)(6) +(6)2 = x2 - 12x + 36
3. (2x − 5)2 = (2x)2 - 2(2x)(5) +(5)2
= 4x2 - 20x + 25

13. Cube of a Binomial:
(a+b)3 = (a + b)(a + b)(a + b) =
(a)3 ± 3(a) 2(b) ± 3(a)(b)2 ± (b) 3
1. (x + 3)3
= (x)3 + 3(x) 2(3) + 3(x)(3)2 + (3) 3
= x3 + 9x 2 + 27x + 27

14. 2. (2x - 5)3
= (2x)3 - 3(2x) 2(5) + 3(2x)(5)2 - (5) 3
= 8x3 - 60x2 + 150x - 125

15. 2. (3x + 7)3
= (3x)3 + 3(3x) 2(7) + 3(3x)(7)2 + (7) 3
= 27x3 + 189x2 + 441x + 343

16. Find the product:
1. 5x2y(7x2 – 4xy2 + 2y3)
2. (4x – 7)(2x – 9)
3. (4x + 3)(7x – 5)
4. (2x2 – 5x)(9x2 + 6x + 4)
5. (6x2 − 4x − 5)(7x3 + 5x − 5)

17. 6. (x − 3)(x + 3)
7. (2x + 3)2
8. (8a2 + 4)(8a2 − 4)
9. (3x − 7)(3x + 7)
10. (2x − 7)3

18. Answers:
1. 35x4y - 20x3y3 + 10x2y4
5. 42x5 − 28x4 − 5x3 – 50x2 – 5x + 25
2. 8x2 - 50x + 63
3. 28x2 + x - 15
4. 18x4 - 33x3 + 38x2 - 20x

19. 6. x2 - 9
7. 4x2 + 24x + 9
8. 64x4 - 16
9. 9x2 - 49
10. 8x3 - 84x2 + 294x - 373

20. Assignment:
1. The dimensions of a window
are 3x + 10 and 2x + 6.
What is the area of the window?
(assuming the window is rectangle)