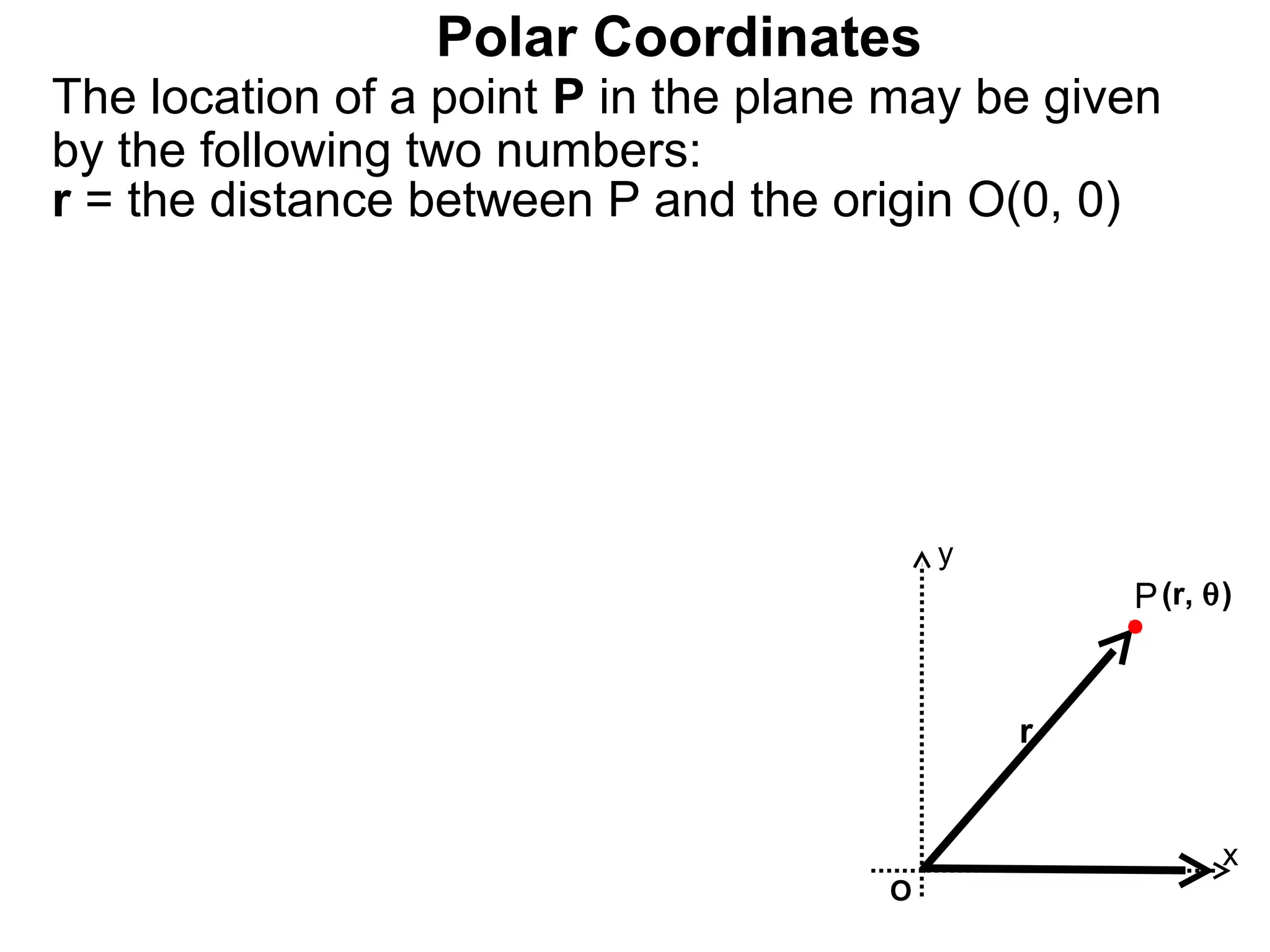
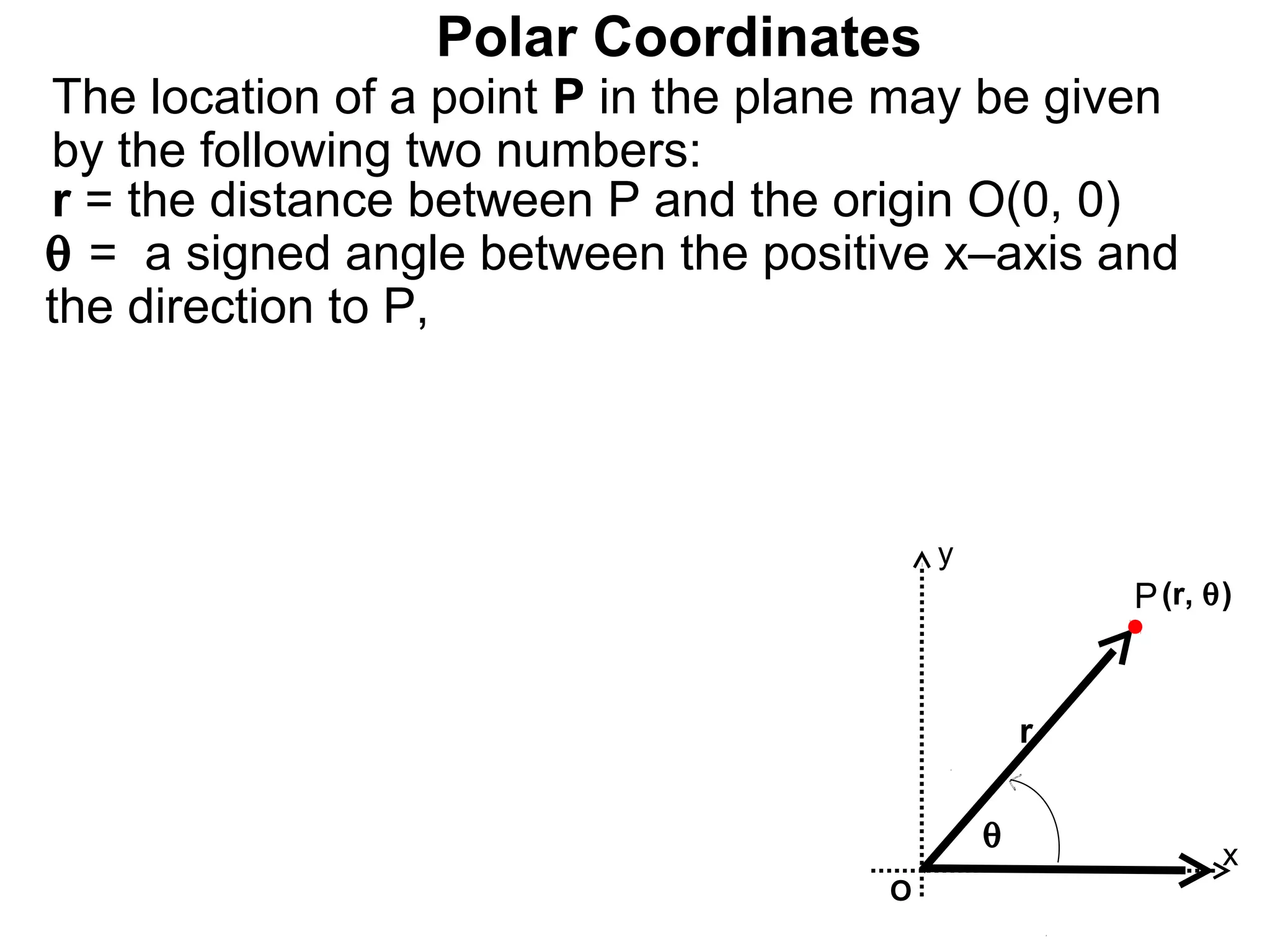
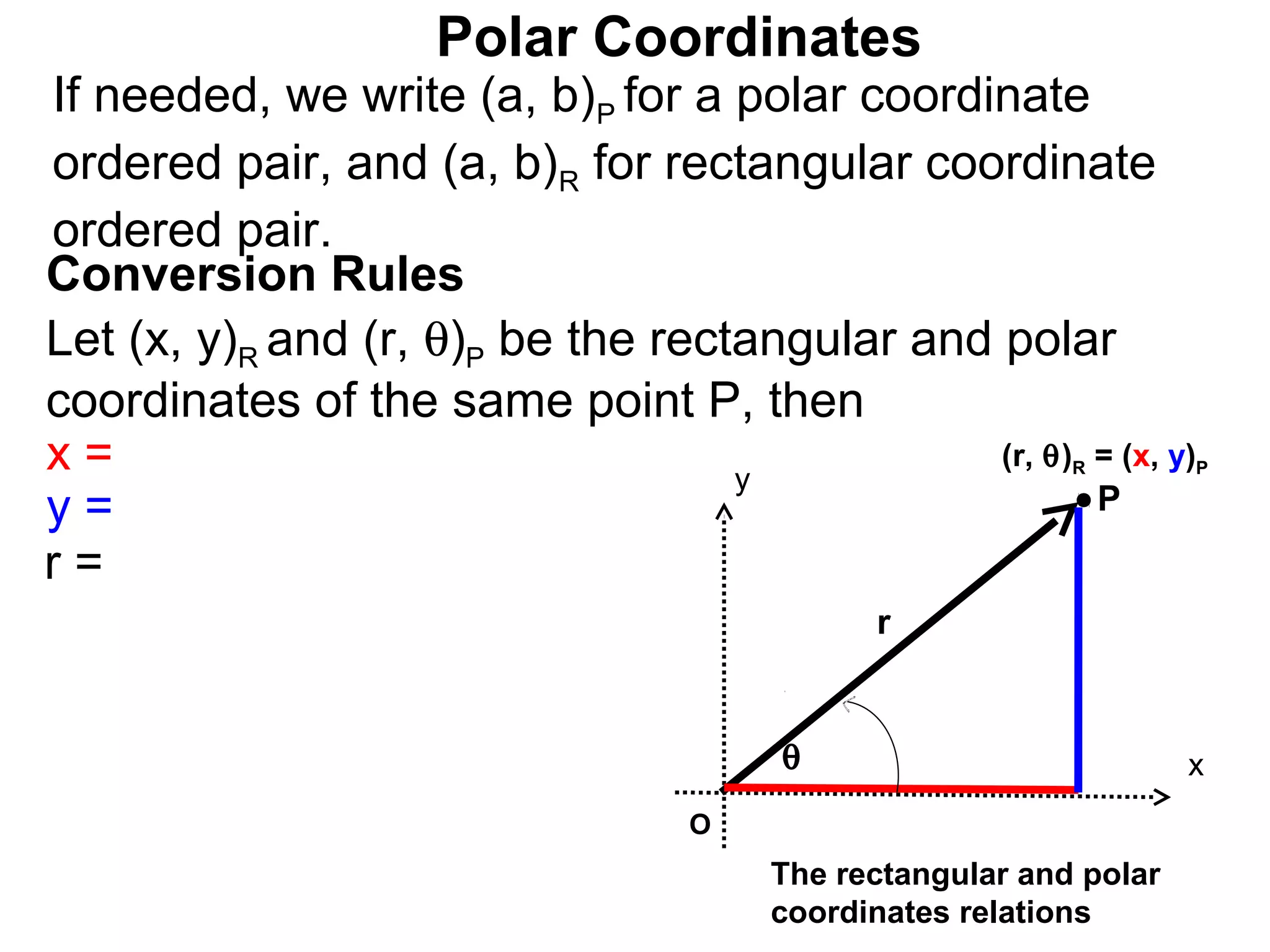
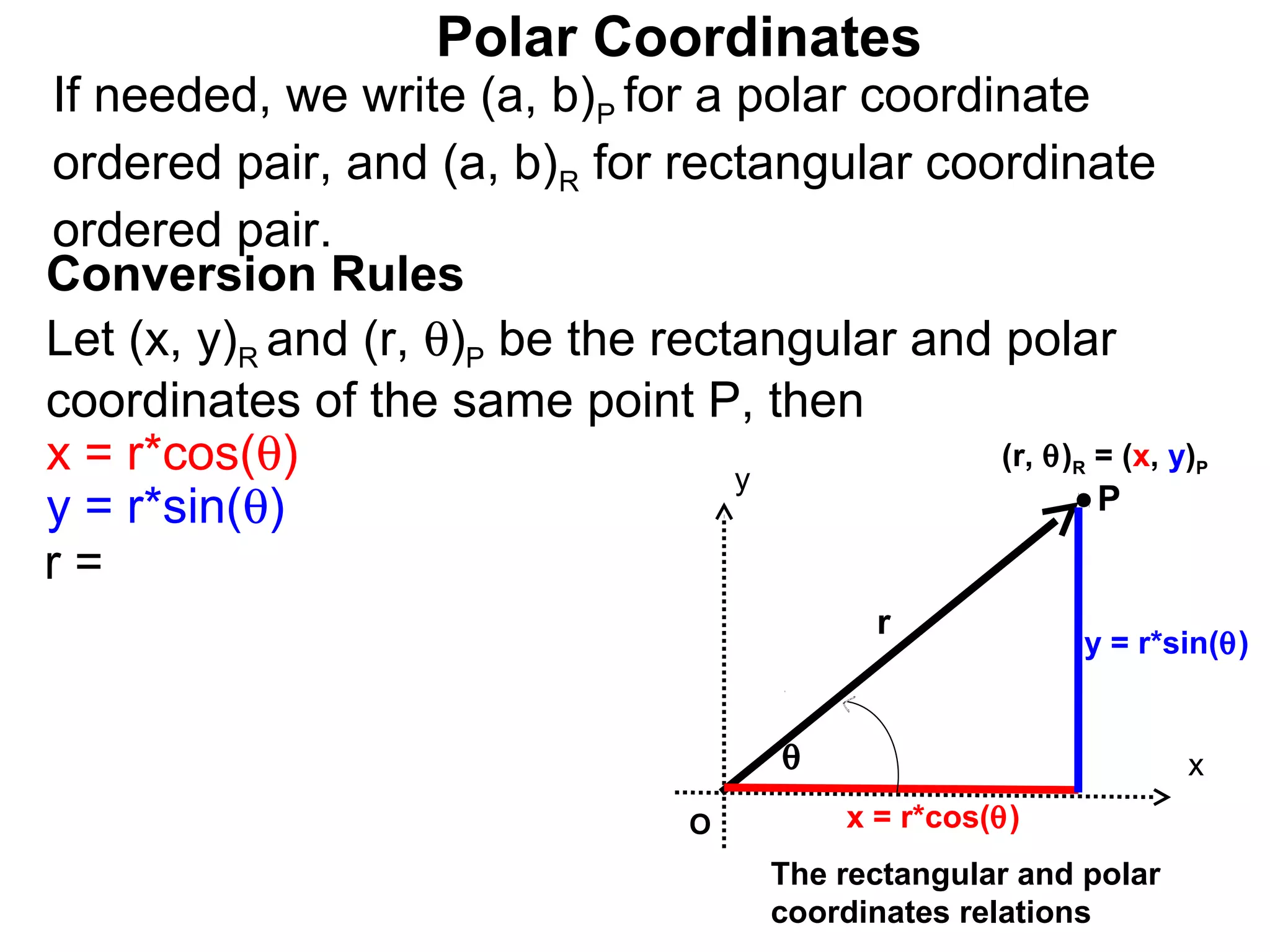
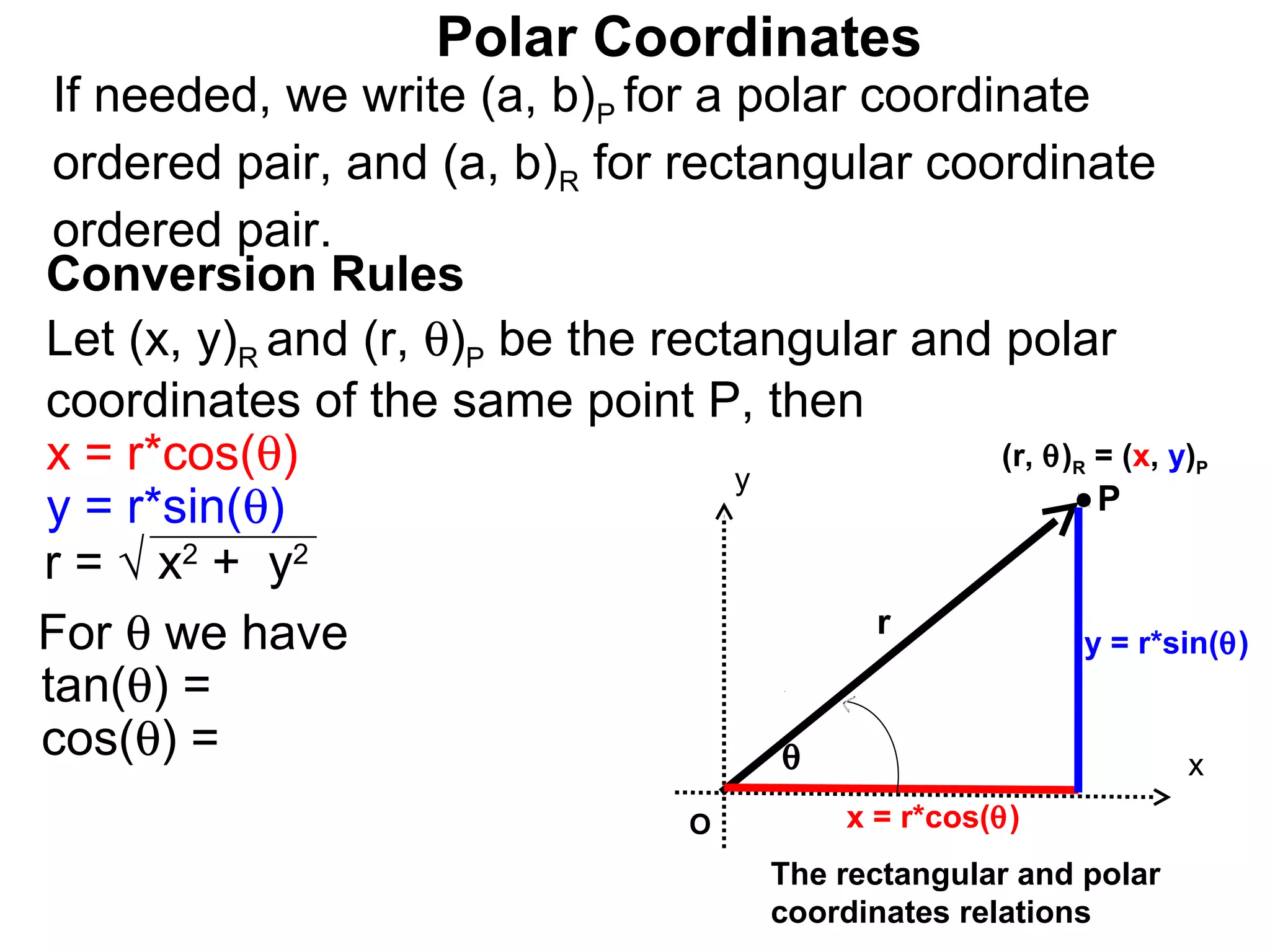
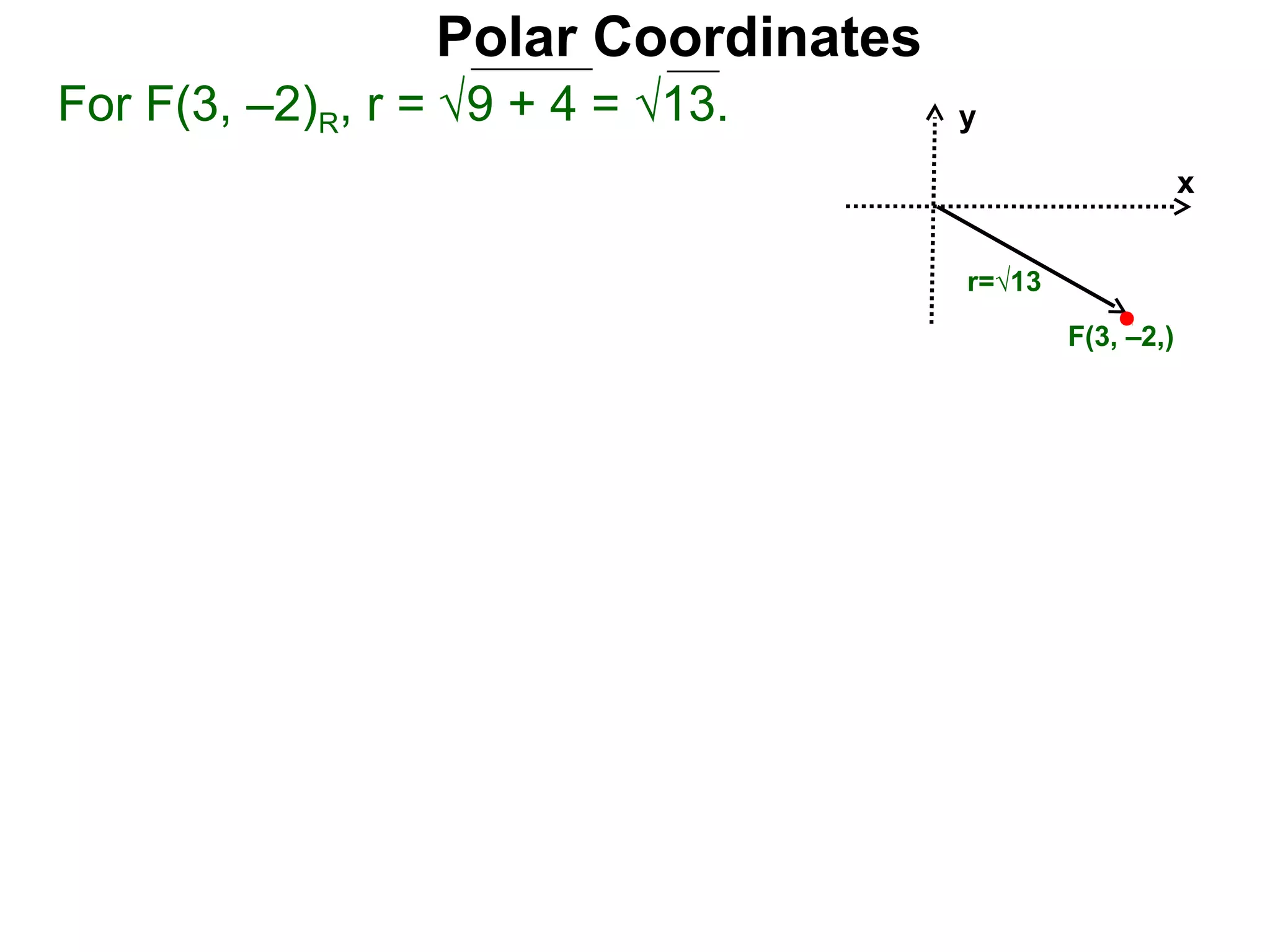
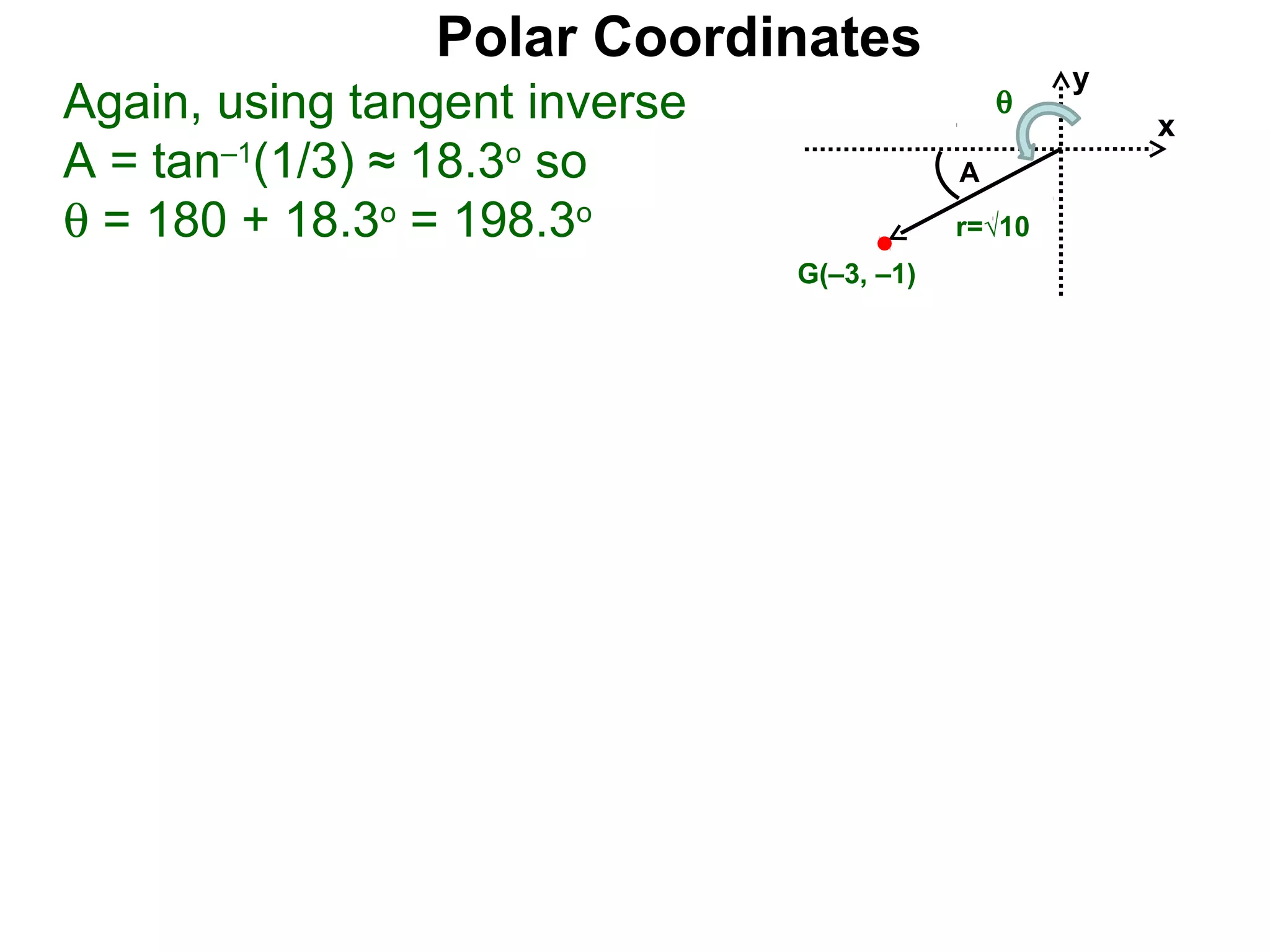
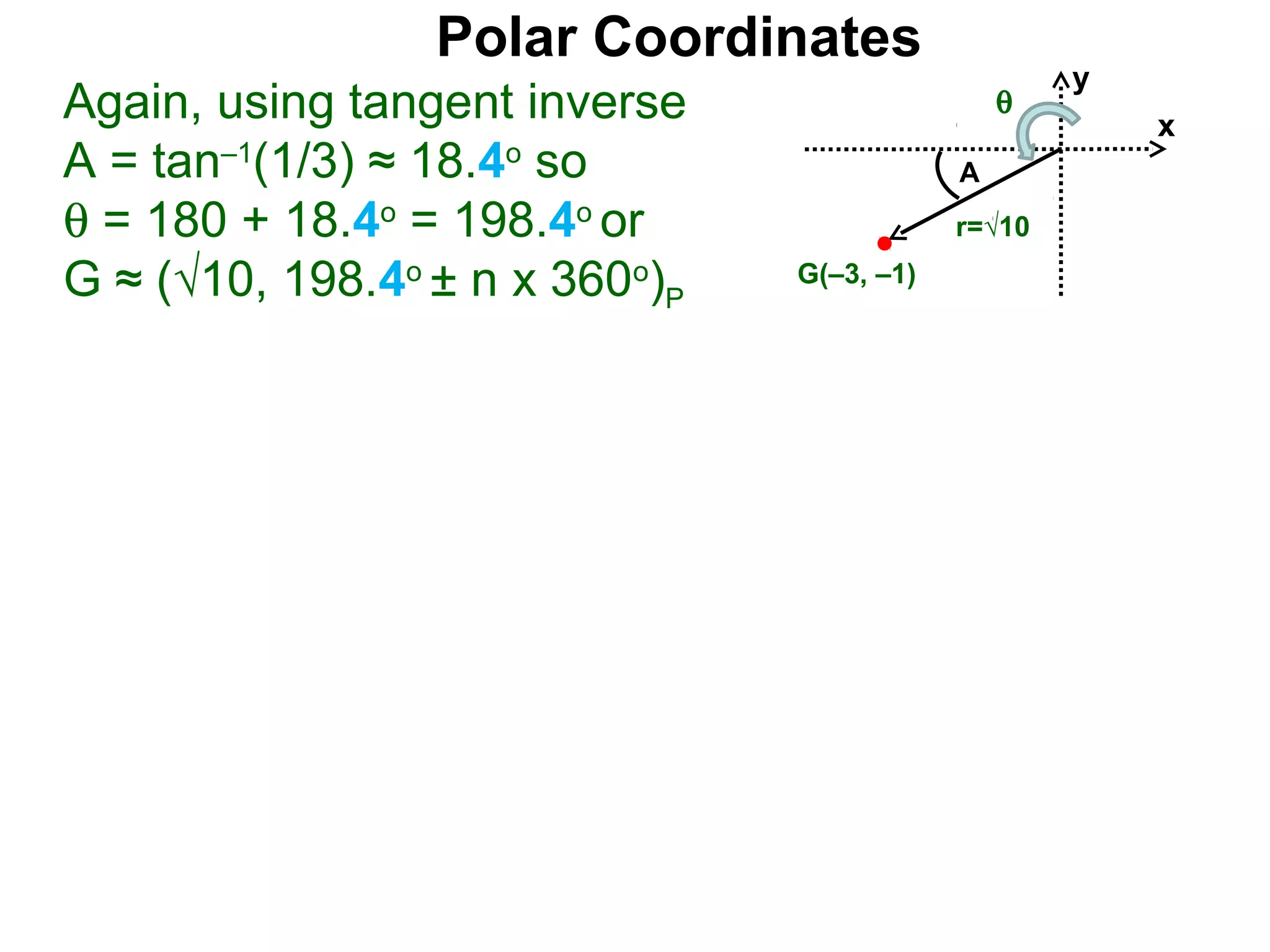
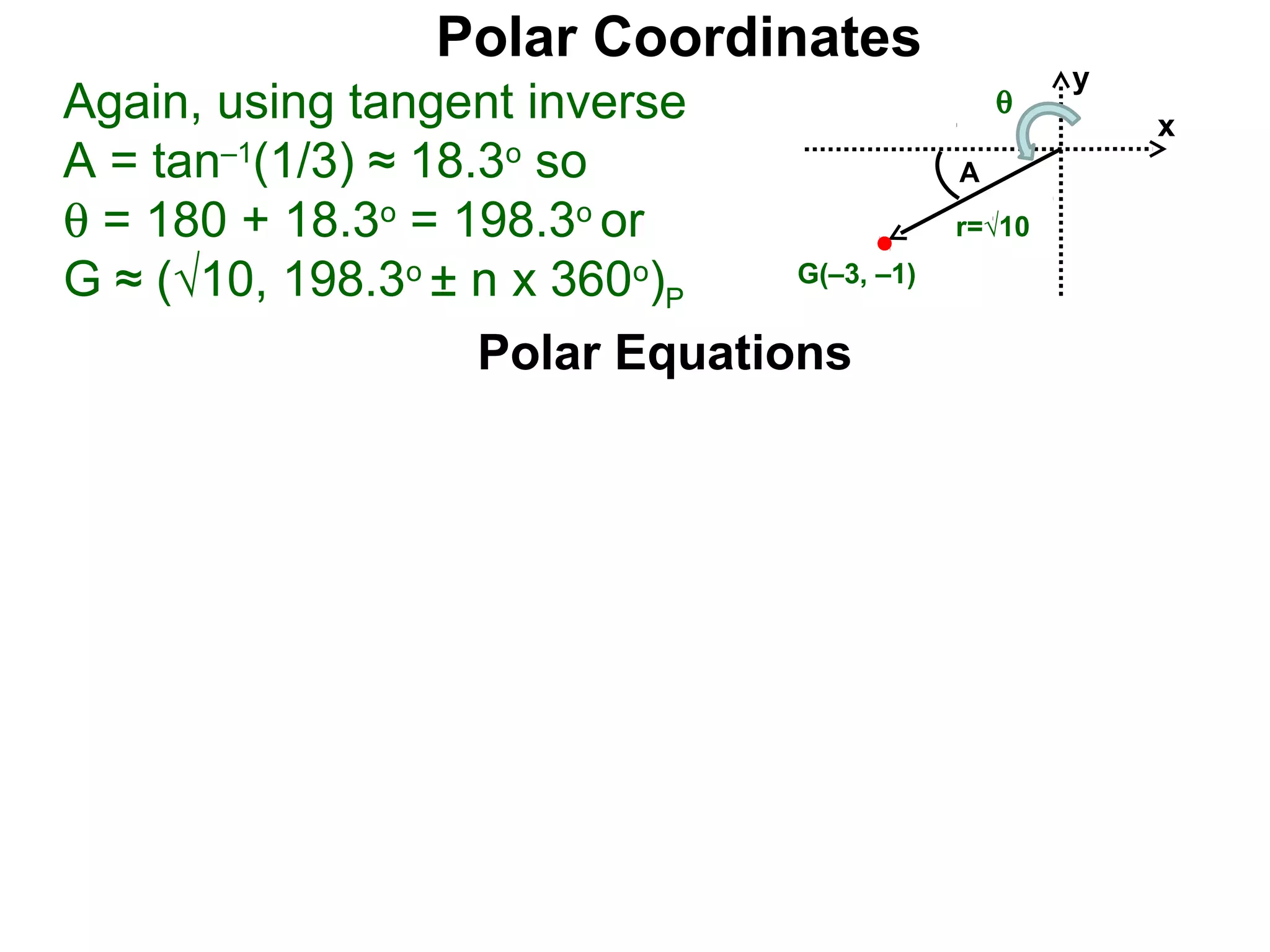
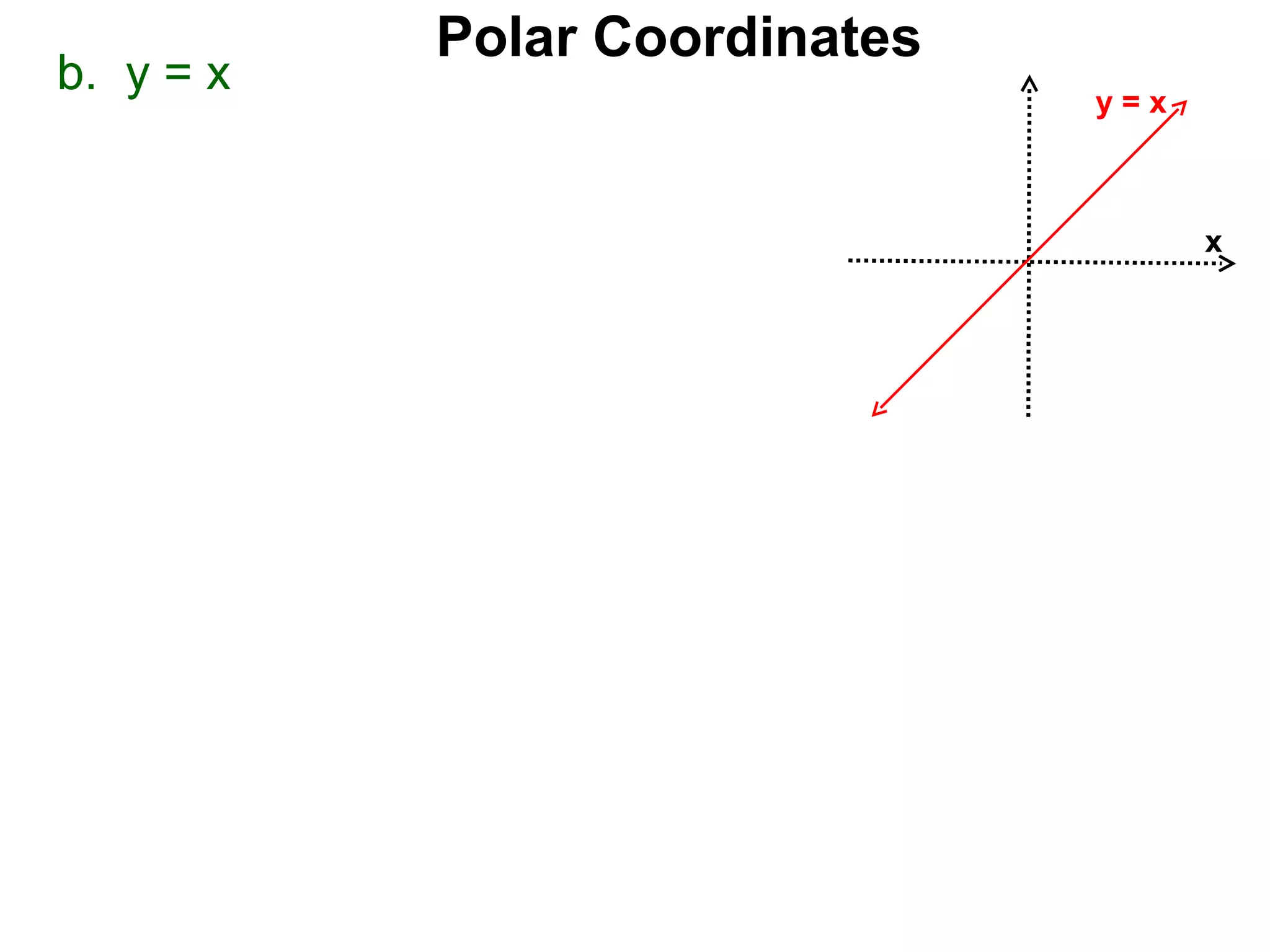
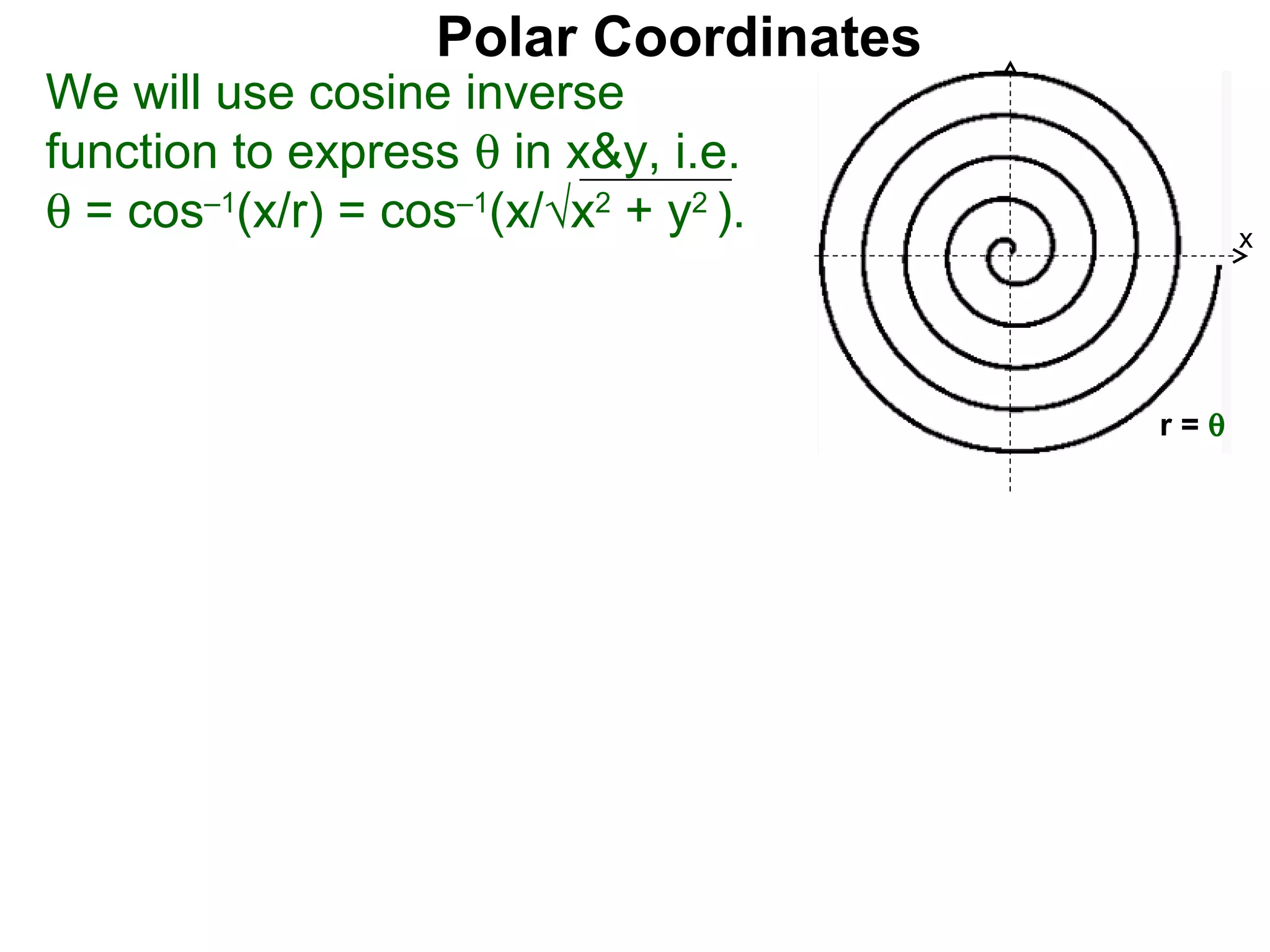
The document describes polar coordinates, which represent the location of a point P in a plane using two numbers: r, the distance from P to the origin O, and θ, the angle between the positive x-axis and the line from O to P. θ is positive for counter-clockwise angles and negative for clockwise angles. The polar coordinate (r, θ) uniquely identifies P's location. The document also provides the conversion formulas between polar coordinates (r, θ) and rectangular coordinates (x, y).

1. Polar Coordinates

2. Polar Coordinates
The location of a point P in the plane may be given
by the following two numbers:
y
P (r, θ)
x
O

3. Polar Coordinates
The location of a point P in the plane may be given
by the following two numbers:
r = the distance between P and the origin O(0, 0)
y
P (r, θ)
r
x
O

4. Polar Coordinates
The location of a point P in the plane may be given
by the following two numbers:
r = the distance between P and the origin O(0, 0)
θ = a signed angle between the positive x–axis and
the direction to P,
y
P (r, θ)
r
θ
x
O

5. Polar Coordinates
The location of a point P in the plane may be given
by the following two numbers:
r = the distance between P and the origin O(0, 0)
θ = a signed angle between the positive x–axis and
the direction to P, specifically,
θ is + for counter clockwise measurements and
θ is – for clockwise measurements .
y
P (r, θ)
r
θ
x
O

6. Polar Coordinates
The location of a point P in the plane may be given
by the following two numbers:
r = the distance between P and the origin O(0, 0)
θ = a signed angle between the positive x–axis and
the direction to P, specifically,
θ is + for counter clockwise measurements and
θ is – for clockwise measurements
The ordered pair (r, θ) is a polar coordinate of P.
y
P (r, θ)
r
θ
x
O

7. Polar Coordinates
The location of a point P in the plane may be given
by the following two numbers:
r = the distance between P and the origin O(0, 0)
θ = a signed angle between the positive x–axis and
the direction to P, specifically,
θ is + for counter clockwise measurements and
θ is – for clockwise measurements
The ordered pair (r, θ) is a polar coordinate of P.
The ordered pairs (r, θ ±2nπ ) with y
n = 0,1, 2, 3… give the same P (r, θ)
geometric information hence lead to
the same location P(r, θ).
r
θ
x
O

8. Polar Coordinates
The location of a point P in the plane may be given
by the following two numbers:
r = the distance between P and the origin O(0, 0)
θ = a signed angle between the positive x–axis and
the direction to P, specifically,
θ is + for counter clockwise measurements and
θ is – for clockwise measurements
The ordered pair (r, θ) is a polar coordinate of P.
The ordered pairs (r, θ ±2nπ ) with y
n = 0,1, 2, 3… give the same P (r, θ)
geometric information hence lead to
the same location P(r, θ).
r
We also use signed distance,
i.e. with negative values of r which
θ
means we are to step backward for x
O
a distance of lrl.

9. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for the rectangular
coordinate ordered pair.

10. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for rectangular coordinate
ordered pair.
Conversion Rules

11. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for rectangular coordinate
ordered pair.
Conversion Rules
Let (x, y)R and (r, θ)P be the rectangular and polar
coordinates of the same point P, then
x= y
(r, θ) = (x, y)
R P
y= P
r=
r
θ x
O
The rectangular and polar
coordinates relations

12. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for rectangular coordinate
ordered pair.
Conversion Rules
Let (x, y)R and (r, θ)P be the rectangular and polar
coordinates of the same point P, then
x = r*cos(θ) y
(r, θ) = (x, y)
R P
y = r*sin(θ) P
r=
r
y = r*sin(θ)
θ x
O x = r*cos(θ)
The rectangular and polar
coordinates relations

13. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for rectangular coordinate
ordered pair.
Conversion Rules
Let (x, y)R and (r, θ)P be the rectangular and polar
coordinates of the same point P, then
x = r*cos(θ) y
(r, θ) = (x, y)
R P
y = r*sin(θ) P
r = √ x2 + y2
r
y = r*sin(θ)
θ x
O x = r*cos(θ)
The rectangular and polar
coordinates relations

14. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for rectangular coordinate
ordered pair.
Conversion Rules
Let (x, y)R and (r, θ)P be the rectangular and polar
coordinates of the same point P, then
x = r*cos(θ) y
(r, θ) = (x, y)
R P
y = r*sin(θ) P
r = √ x2 + y2
For θ we have r
y = r*sin(θ)
tan(θ) =
cos(θ) = θ x
O x = r*cos(θ)
The rectangular and polar
coordinates relations

15. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for rectangular coordinate
ordered pair.
Conversion Rules
Let (x, y)R and (r, θ)P be the rectangular and polar
coordinates of the same point P, then
x = r*cos(θ) y
(r, θ) = (x, y)
R P
y = r*sin(θ) P
r = √ x2 + y2
For θ we have r
y = r*sin(θ)
tan(θ) = y/x
cos(θ) = x/√x2 + y2 θ x
x = r*cos(θ)
The rectangular and polar
coordinates relations

16. Polar Coordinates
If needed, we write (a, b)P for a polar coordinate
ordered pair, and (a, b)R for rectangular coordinate
ordered pair.
Conversion Rules
Let (x, y)R and (r, θ)P be the rectangular and polar
coordinates of the same point P, then
x = r*cos(θ) y
(r, θ) = (x, y)
R P
y = r*sin(θ) P
r = √ x2 + y2
For θ we have r
y = r*sin(θ)
tan(θ) = y/x
cos(θ) = x/√x2 + y2 or using θ x
inverse trig. functions that O x = r*cos(θ)
θ = tan–1(y/x) The rectangular and polar
θ = cos–1 (x/√x2 + y2) coordinates relations

17. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.

18. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P y
x
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

19. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P y A(4, 60 ) o
P
4
60o x
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

20. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)),
4
60o x
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

21. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)),
4
= (2, 2√3)
60o x
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

22. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)),
4
= (2, 2√3)
for B(5, 0o)P, (x, y) = (5, 0), 60 o
x
B(5, 0)P
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

23. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)),
4
= (2, 2√3)
for B(5, 0o)P, (x, y) = (5, 0), 60 o
x
–45 o
B(5, 0)
for C and D, P
4
C
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

24. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)), 3π/4
4
= (2, 2√3)
for B(5, 0o)P, (x, y) = (5, 0), 60 o
x
–45 o
B(5, 0)
for C and D, P
4 C
&
D
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

25. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P D
y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)), 3π/4
4
= (2, 2√3)
for B(5, 0o)P, (x, y) = (5, 0), 60 o
x
–45 o
B(5, 0)
for C and D, P
4
C
C(4, –45o)P
= D(–4, 3π/4 rad)P
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

26. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P D
y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)), 3π/4
4
= (2, 2√3)
for B(5, 0o)P, (x, y) = (5, 0), 60 o
x
–45 o
B(5, 0)
for C and D, P
(x, y)R = (4cos(–45), 4sin(–45)) 4
C
= (–4cos(3π/4), –4sin(3π/4)) C(4, –45 ) o
P
= D(–4, 3π/4 rad)P
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

27. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P D
y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)), 3π/4
4
= (2, 2√3)
for B(5, 0o)P, (x, y) = (5, 0), 60 o
x
–45 o
B(5, 0)
for C and D, P
(x, y)R = (4cos(–45), 4sin(–45)) 4
C
= (–4cos(3π/4), –4sin(3π/4)) C(4, –45 ) o
P
= (2√2, –2√2) = D(–4, 3π/4 rad) P
x = r*cos(θ) r2 = x2 + y2
y = r*sin(θ) tan(θ) = y/x

28. Polar Coordinates
Example A. a. Plot the following polar coordinates
A(4, 60o)P , B(5, 0o)P, C(4, –45o)P, D(–4, 3π/4 rad)P.
Find their corresponding rectangular coordinates.
For A(4, 60o)P D
y A(4, 60 ) o
P
(x, y)R = (4*cos(60), 4*sin(60)), 3π/4
4
= (2, 2√3)
for B(5, 0o)P, (x, y) = (5, 0), 60 o
x
–45 o
B(5, 0)
for C and D, P
(x, y)R = (4cos(–45), 4sin(–45)) 4
C
= (–4cos(3π/4), –4sin(3π/4)) C(4, –45 ) o
P
= (2√2, –2√2) = D(–4, 3π/4 rad) P
Converting rectangular positions
into polar coordinates requires x = r*cos(θ) r = x + y
2 2 2
y = r*sin(θ) tan(θ) = y/x
more care.

29. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.

30. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
y
E(–4, 3)
x

31. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
y
E(–4, 3)
x

32. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
hence for E, r = √16 + 9 = 5. y
E(–4, 3)
r=5
x

33. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
hence for E, r = √16 + 9 = 5. y
There is no single formula that
would give θ. E(–4, 3)
θ
r=5
x

34. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
hence for E, r = √16 + 9 = 5. y
There is no single formula that
would give θ. This is because θ has E(–4, 3) θ
to be expressed via the inverse r=5
x
trig–functions hence the position of
E dictates which inverse function
would be easier to use to extract θ.

35. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
hence for E, r = √16 + 9 = 5. y
There is no single formula that
would give θ. This is because θ has E(–4, 3) θ
to be expressed via the inverse r=5
x
trig–functions hence the position of
E dictates which inverse function
would be easier to use to extract θ. Since E is in the
2nd quadrant, the angle θ may be recovered by the
cosine inverse function (why?).

36. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
hence for E, r = √16 + 9 = 5. y
There is no single formula that
would give θ. This is because θ has E(–4, 3) θ
to be expressed via the inverse r=5
x
trig–functions hence the position of
E dictates which inverse function
would be easier to use to extract θ. Since E is the 2nd
quadrant, the angle θ may be recovered by the cosine
inverse function (why?). So θ = cos–1(–4/5) ≈ 143o

37. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
hence for E, r = √16 + 9 = 5. y
There is no single formula that
would give θ. This is because θ has E(–4, 3) θ
to be expressed via the inverse r=5
x
trig–functions hence the position of
E dictates which inverse function
would be easier to use to extract θ. Since E is the 2nd
quadrant, the angle θ may be recovered by the cosine
inverse function (why?). So θ = cos–1(–4/5) ≈ 143o
or that E(–4, 3)R ≈ (5, 143o)P

38. Polar Coordinates
b. Find a polar coordinate then list all possible polar
coordinates for each of the following points
(with r > 0): E(–4, 3)R, F(3, –2)R, and G(–3, –1)R.
We have the distance formula r = √x2 + y2,
hence for E, r = √16 + 9 = 5. y
There is no single formula that
would give θ. This is because θ has E(–4, 3) θ
to be expressed via the inverse r=5
x
trig–functions hence the position of
E dictates which inverse function
would be easier to use to extract θ. Since E is the 2nd
quadrant, the angle θ may be recovered by the cosine
inverse function (why?). So θ = cos–1(–4/5) ≈ 143o
or that E(–4, 3)R ≈ (5, 143o)P = (5, 143o±n*360o)P

39. Polar Coordinates
For F(3, –2)R, y
x
F(3, –2,)

40. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
x
r=√13
F(3, –2,)

41. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
Since F is in the 4th quadrant, the x
angle θ may be recovered by the θ
sine inverse or the tangent inverse r=√13
function. F(3, –2,)

42. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
Since F is the 4th quadrant, the x
angle θ may be recovered by the θ
sine inverse or the tangent inverse r=√13
function. The tangent inverse has F(3, –2,)
the advantage of obtaining the answer directly from
the x and y coordinates.

43. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
Since F is the 4th quadrant, the x
angle θ may be recovered by the θ
sine inverse or the tangent inverse r=√13
function. The tangent inverse has F(3, –2,)
the advantage of obtaining the answer directly from
the x and y coordinates. So θ = tan–1(–2/3)
≈ –0.588rad and that F(3, –2)R ≈ (√13, –0.588rad)P

44. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
Since F is the 4th quadrant, the x
angle θ may be recovered by the θ
sine inverse or the tangent inverse r=√13
function. The tangent inverse has F(3, –2,)
the advantage of obtaining the answer directly from
the x and y coordinates. So θ = tan–1(–2/3)
≈ –0.588rad and that F(3, –2)R ≈ (√13, –0.588rad)P
= (√13, –0.588rad ± 2nπ)P

45. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
Since F is the 4th quadrant, the x
angle θ may be recovered by the θ
sine inverse or the tangent inverse r=√13
function. The tangent inverse has F(3, –2,)
the advantage of obtaining the answer directly from
the x and y coordinates. So θ = tan–1(–2/3)
≈ –0.588rad and that F(3, –2)R ≈ (√13, –0.588rad)P
= (√13, –0.588rad ± 2nπ)P
y
For G(–3, –1)R, r = √9 + 1 = √10.
x
r=√10
G(–3, –1)

46. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
Since F is the 4th quadrant, the x
angle θ may be recovered by the θ
sine inverse or the tangent inverse r=√13
function. The tangent inverse has F(3, –2,)
the advantage of obtaining the answer directly from
the x and y coordinates. So θ = tan–1(–2/3)
≈ –0.588rad and that F(3, –2)R ≈ (√13, –0.588rad)P
= (√13, –0.588rad ± 2nπ)P
y
For G(–3, –1)R, r = √9 + 1 = √10.
G is the 3rd quadrant. Hence θ can’t x
be obtained directly via the inverse– r=√10
trig functions. G(–3, –1)

47. Polar Coordinates
For F(3, –2)R, r = √9 + 4 = √13. y
Since F is the 4th quadrant, the x
angle θ may be recovered by the θ
sine inverse or the tangent inverse r=√13
function. The tangent inverse has F(3, –2,)
the advantage of obtaining the answer directly from
the x and y coordinates. So θ = tan–1(–2/3)
≈ –0.588rad and that F(3, –2)R ≈ (√13, –0.588rad)P
= (√13, –0.588rad ± 2nπ)P
y
For G(–3, –1)R, r = √9 + 1 = √10.
G is the 3rd quadrant. Hence θ can’t x
A
be obtained directly via the inverse– r=√10
trig functions. We will find the angle G(–3, –1)
A as shown first, then θ = A + π.

48. Polar Coordinates
y
Again, using tangent inverse x
A = tan–1(1/3) ≈ 18.4o A
r=√10
G(–3, –1)

49. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.3o so A
θ = 180 + 18.3o = 198.3o r=√10
G(–3, –1)

50. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.4o so A
θ = 180 + 18.4o = 198.4o or r=√10
G ≈ (√10, 198.4o ± n x 360o)P G(–3, –1)

51. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.3o so A
θ = 180 + 18.3o = 198.3o or r=√10
G ≈ (√10, 198.3o ± n x 360o)P G(–3, –1)
Polar Equations

52. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.3o so A
θ = 180 + 18.3o = 198.3o or r=√10
G ≈ (√10, 198.3o ± n x 360o)P G(–3, –1)
Polar Equations
A polar equation is a description of the relation
between points using their distances and directions.

53. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.3o so A
θ = 180 + 18.3o = 198.3o or r=√10
G ≈ (√10, 198.3o ± n x 360o)P G(–3, –1)
Polar Equations
A polar equation is a description of the relation
between points using their distances and directions. In
symbols, polar equations look like our old equations
except that x and y are replaced with r and θ.

54. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.3o so A
θ = 180 + 18.3o = 198.3o or r=√10
G ≈ (√10, 198.3o ± n x 360o)P G(–3, –1)
Polar Equations
A polar equation is a description of relation between
points using their distances and directions. In symbols,
polar equations look like our old equations except that
x and y are replaced with r and θ. However, the
geometry described respectively by the symbols are
completely different.

55. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.3o so A
θ = 180 + 18.3o = 198.3o or r=√10
G ≈ (√10, 198.3o ± n x 360o)P G(–3, –1)
Polar Equations
A polar equation is a description of relation between
points using their distances and directions. In symbols,
polar equations look like our old equations except that
x and y are replaced with r and θ. However, the
geometry described respectively by the symbols are
completely different. We use the x = r*cos(θ)
conversion rules to translate y = r*sin(θ)
equations between the two systems. r = √x2 + y2
tan(θ) = y/x

56. Polar Coordinates
y
Again, using tangent inverse θ
x
A = tan–1(1/3) ≈ 18.3o so A
θ = 180 + 18.3o = 198.3o or r=√10
G ≈ (√10, 198.3o ± n x 360o)P G(–3, –1)
Polar Equations
A polar equation is a description of relation between
points using their distances and directions. In symbols,
polar equations look like our old equations except that
x and y are replaced with r and θ. However, the
geometry described respectively by the symbols are
completely different. We use the x = r*cos(θ)
conversion rules to translate y = r*sin(θ)
equations between the two systems. r = √x2 + y2
Let’s start with some basic equations. tan(θ) = y/x

57. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.

58. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.
Example B. Convert each of the following rectangular
equations into the corresponding polar form.
Write the answer in the r = f(θ) form and interpret its
geometric significances in terms of distances and
directions.

59. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.
Example B. Convert each of the following rectangular
equations into the corresponding polar form.
Write the answer in the r = f(θ) form and interpret its
geometric significances in terms of distances and
directions.
a. x = k
x
x=k

60. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.
Example B. Convert each of the following rectangular
equations into the corresponding polar form.
Write the answer in the r = f(θ) form and interpret its
geometric significances in terms of distances and
directions.
a. x = k
Replacing x with r*cos(θ)
we get that r*cos(θ) = k
x
x=k

61. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.
Example B. Convert each of the following rectangular
equations into the corresponding polar form.
Write the answer in the r = f(θ) form and interpret its
geometric significances in terms of distances and
directions.
a. x = k
Replacing x with r*cos(θ)
we get that r*cos(θ) = k
or that r = k*sec(θ) = f(θ). x
x=k

62. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.
Example B. Convert each of the following rectangular
equations into the corresponding polar form.
Write the answer in the r = f(θ) form and interpret its
geometric significances in terms of distances and
directions.
a. x = k
Replacing x with r*cos(θ)
we get that r*cos(θ) = k
or that r = k*sec(θ) = f(θ). x
In the picture, r = k*sec(θ) gives
the basic trig. relation of points
on the vertical line x = k as
x=k

63. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.
Example B. Convert each of the following rectangular
equations into the corresponding polar form.
Write the answer in the r = f(θ) form and interpret its
geometric significances in terms of distances and
directions.
a. x = k (k, y)
Replacing x with r*cos(θ)
we get that r*cos(θ) = k
or that r = k*sec(θ) = f(θ). θ x
In picture, r = k*sec(θ) gives the k
basic trig. relation of points on
the vertical line x = k as shown.
x=k

64. Polar Coordinates
Equations in x and y are called rectangular equations
and equations in r and θ are called polar equations.
Example B. Convert each of the following rectangular
equations into the corresponding polar form.
Write the answer in the r = f(θ) form and interpret its
geometric significances in terms of distances and
directions.
a. x = k (k, y)
Replacing x with r*cos(θ)
we get that r*cos(θ) = k r = k*sec(θ )
or that r = k*sec(θ) = f(θ). θ x
In picture, r = k*sec(θ) gives the k
basic trig. relation of points on
the vertical line x = k as shown.
x=k

65. Polar Coordinates
b. y = x y=x
x

66. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
r*sin(θ) = r*cos(θ), x

67. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),

68. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),
dividing by cos(θ) we have that
tan(θ) = 1

69. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
θ = π/4.
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),
dividing by cos(θ) we have that
tan(θ) = 1 or that θ
= π/4 ± nπ.

70. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
θ = π/4.
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),
dividing by cos(θ) we have that
tan(θ) = 1 or that θ
The equation θ = π/4 is a polar constant equation.
= π/4 ± nπ.

71. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
θ = π/4.
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),
dividing by cos(θ) we have that
tan(θ) = 1 or that θ
The equation θ = π/4 is a polar constant equation.
= π/4 ± nπ.
Since the variable r is missing, r can be of any value.

72. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
θ = π/4.
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),
dividing by cos(θ) we have that
tan(θ) = 1 or that θ
The equation θ = π/4 is a polar constant equation.
= π/4 ± nπ.
Since the variable r is missing, r can be of any value.
Geometrically, it says that the diagonal line y = x
consists of those points whose polar angles θ = π/4.

73. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
θ = π/4.
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),
dividing by cos(θ) we have that
tan(θ) = 1 or that θ
The equation θ = π/4 is a polar constant equation.
= π/4 ± nπ.
Since the variable r is missing, r can be of any value.
Geometrically, it says that the diagonal line y = x
consists of those points whose polar angles θ = π/4.
Note that there are infinitely many non–equivalent
polar equations that define the same set of diagonal
points.

74. Polar Coordinates
b. y = x y=x
For y = x, replace x = r*cos(θ)
and y = r*sin(θ), we get that
θ = π/4.
r*sin(θ) = r*cos(θ), assuming r ≠ 0, x
we have sin(θ) = cos(θ),
dividing by cos(θ) we have that
tan(θ) = 1 or that θ
The equation θ = π/4 is a polar constant equation.
= π/4 ± nπ.
Since the variable r is missing, r can be of any value.
Geometrically, it says that the diagonal line y = x
consists of those points whose polar angles θ = π/4.
Note that there are infinitely many non–equivalent
polar equations that define the same set of diagonal
points. Specifically that θ = 5π/4, θ = 9π/4, ..,
θ = –3π/4, θ = –7π/4, .. all give y = x.

75. Polar Coordinates
The non–uniqueness of the polar form is the major
difference between the rectangular & polar systems

76. Polar Coordinates
The non–uniqueness of the polar form is the major
difference between the rectangular & polar systems.
Steps employed and solutions obtained in the
rectangular x&y equations, when applied to the r&θ
polar equations, have to be reinterpreted in light of the
polar geometry.

77. Polar Coordinates
The non–uniqueness of the polar form is the major
difference between the rectangular & polar systems.
Steps employed and solutions obtained in the
rectangular x&y equations, when applied to the r&θ
polar equations, have to be reinterpreted in light of the
polar geometry.
Example C. Interpret and draw the graph of each of
the following polar equations. Convert each equation
into a corresponding rectangular form.
a. r = k

78. Polar Coordinates
The non–uniqueness of the polar form is the major
difference between the rectangular & polar systems.
Steps employed and solutions obtained in the
rectangular x&y equations, when applied to the r&θ
polar equations, have to be reinterpreted in light of the
polar geometry.
Example C. Interpret and draw the graph of each of
the following polar equations. Convert each equation
into a corresponding rectangular form.
a. r = k
The polar equation states that the
distance r, from the origin to our points,
is a constant k.

79. Polar Coordinates
The non–uniqueness of the polar form is the major
difference between the rectangular & polar systems.
Steps employed and solutions obtained in the
rectangular x&y equations, when applied to the r&θ
polar equations, have to be reinterpreted in light of the
polar geometry.
Example C. Interpret and draw the graph of each of
the following polar equations. Convert each equation
into a corresponding rectangular form.
a. r = k
The polar equation states that the r=k x
distance r, from the origin to our points,
is a constant k. This is the circle of
radius k, centered at (0, 0).

80. Polar Coordinates
Set r = √x2 + y2 = k we have that
x2 + y2 = k2 in the rectangular form.
r=k x

81. Polar Coordinates
Set r = √x2 + y2 = k we have that
x2 + y2 = k2 in the rectangular form.
r=k x
b. r = θ

82. Polar Coordinates
Set r = √x2 + y2 = k we have that
x2 + y2 = k2 in the rectangular form.
r=k x
b. r = θ
Let θ > 0 (in radian), the polar equation
states that the distance r is of the same
as θ.

83. Polar Coordinates
Set r = √x2 + y2 = k we have that
x2 + y2 = k2 in the rectangular form.
r=k x
b. r = θ
Let θ > 0 (in radian), the polar equation
states that the distance r is of the same
as θ. Hence starting at (0, 0)P, as
θ increases, r increases, so the points
are circling outward from the
origin at a steady or linear rate.

84. Polar Coordinates
Set r = √x2 + y2 = k we have that
x2 + y2 = k2 in the rectangular form.
r=k x
b. r = θ
Let θ > 0 (in radian), the polar equation
states that the distance r is of the same
as θ. Hence starting at (0, 0)P, as
θ increases, r increases, so the points x
are circling outward from the
origin at a steady or linear rate. r=θ
In general, the graph of r = f(θ) where
f(θ) is an increasing or decreasing
function is called a spiral.

85. Polar Coordinates
Set r = √x2 + y2 = k we have that
x2 + y2 = k2 in the rectangular form.
r=k x
b. r = θ
Let θ > 0 (in radian), the polar equation
states that the distance r is of the same
as θ. Hence starting at (0, 0)P, as
θ increases, r increases, so the points x
are circling outward from the
origin at a steady or linear rate. r=θ
In general, the graph of r = f(θ) where Archimedean spirals
f(θ) is an increasing or decreasing
function is called a spiral. A uniformly
banded spiral such as this one is called
an Archimedean spiral.

86. Polar Coordinates
We will use cosine inverse
function to express θ in x&y,
x
x
r=θ

87. Polar Coordinates
We will use cosine inverse
function to express θ in x&y, i.e.
θ = cos–1(x/r) = cos–1(x/√x2 + y2 ). x
x
r=θ

88. Polar Coordinates
We will use cosine inverse
function to express θ in x&y, i.e.
θ = cos–1(x/r) = cos–1(x/√x2 + y2 ). x
We have the equation that
cos–1(x/√x2 + y2) = √x2 + y2 ( = r ) x
r=θ

89. Polar Coordinates
We will use cosine inverse
function to express θ in x&y, i.e.
θ = cos–1(x/r) = cos–1(x/√x2 + y2 ). x
We have the equation that
cos–1(x/√x2 + y2) = √x2 + y2 ( = r ) x
This rectangular equation only r=θ
gives the part of the spiral where
0 < √x2 + y2 ≤ π (why?)

90. Polar Coordinates
We will use cosine inverse
function to express θ in x&y, i.e.
θ = cos–1(x/r) = cos–1(x/√x2 + y2 ). x
We have the equation that
cos–1(x/√x2 + y2) = √x2 + y2 ( = r ) x
This rectangular equation only r=θ
gives the part of the spiral where
0 < √x2 + y2 ≤ π (why?)
x
cos–1(x/√x2 + y2) = √x2 + y2
The “Lost in Translation”
from the polar to the
rectangular equation

91. Polar Coordinates
We will use cosine inverse
function to express θ in x&y, i.e.
θ = cos–1(x/r) = cos–1(x/√x2 + y2 ). x
We have the equation that
cos–1(x/√x2 + y2) = √x2 + y2 ( = r ) x
This rectangular equation only r=θ
gives the part of the spiral where
0 < √x2 + y2 ≤ π (why?)
For other segments of the
spirals, we add nπ with n = 1,2,..
x
cos–1(x/√x2 + y2) = √x2 + y2
The “Lost in Translation”
from the polar to the
rectangular equation

92. Polar Coordinates
We will use cosine inverse
function to express θ in x&y, i.e.
θ = cos–1(x/r) = cos–1(x/√x2 + y2 ). x
We have the equation that
cos–1(x/√x2 + y2) = √x2 + y2 ( = r ) x
This rectangular equation only r=θ
gives the part of the spiral where
0 < √x2 + y2 ≤ π (why?)
For other parts of the spirals,
we add nπ to θ with n = 1,2,.. to
obtain more distant segments, so x
cos–1(x/√x2 + y2) + nπ = √x2 + y2. cos–1(x/√x2 + y2) = √x2 + y2
The “Lost in Translation”
from the polar to the
rectangular equation

93. Polar Coordinates
We will use cosine inverse
function to express θ in x&y, i.e.
θ = cos–1(x/r) = cos–1(x/√x2 + y2 ). x
We have the equation that
cos–1(x/√x2 + y2) = √x2 + y2 ( = r ) x
This rectangular equation only r=θ
gives the part of the spiral where
0 < √x2 + y2 ≤ π (why?)
For other parts of the spirals,
we add nπ to θ with n = 1,2,.. to
obtain more distant segments, so x
cos–1(x/√x2 + y2) + nπ = √x2 + y2. cos–1(x/√x2 + y2) = √x2 + y2
The “Lost in Translation”
This shows the advantages of the from the polar to the
polar system in certain settings. rectangular equation