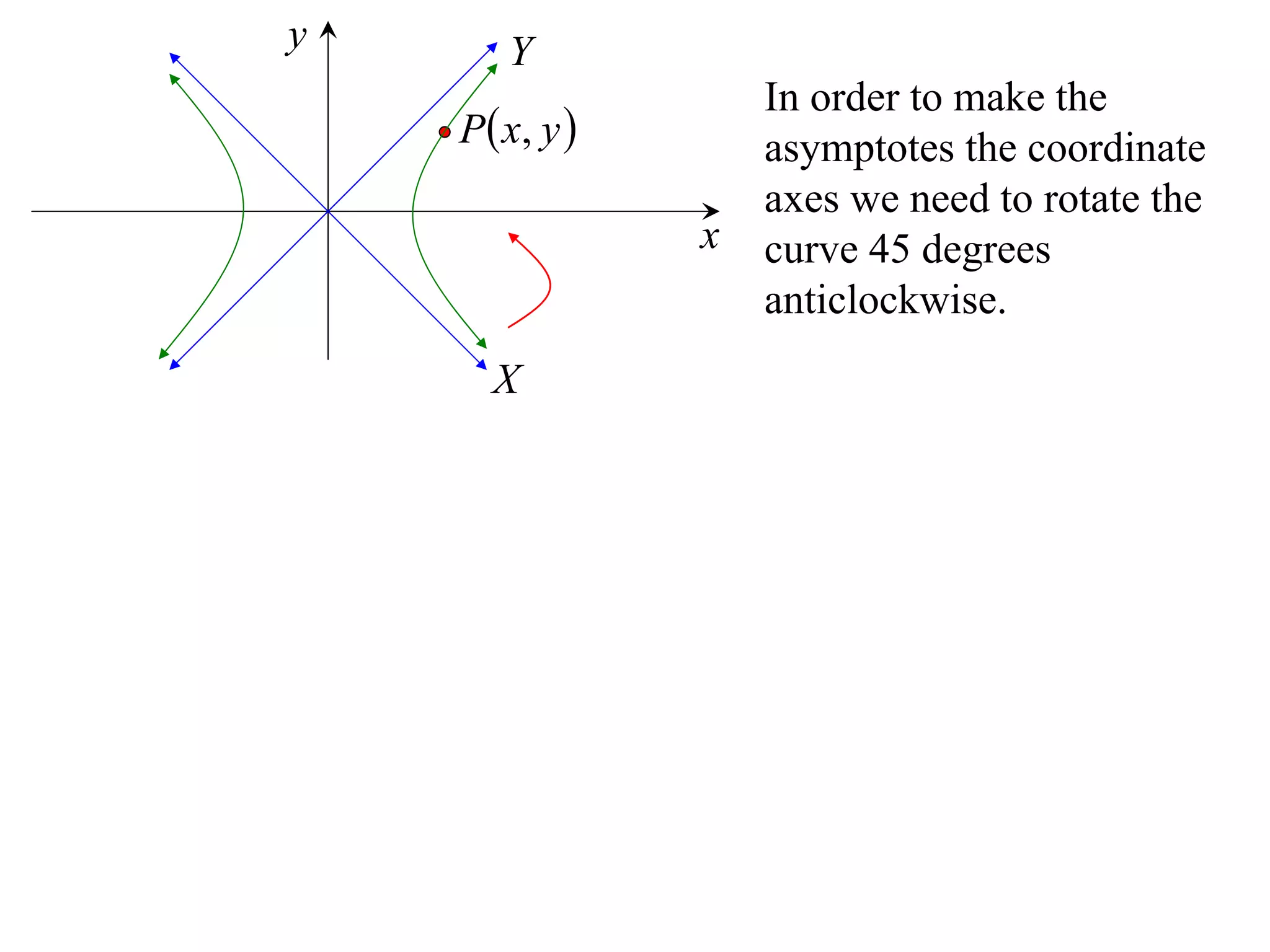
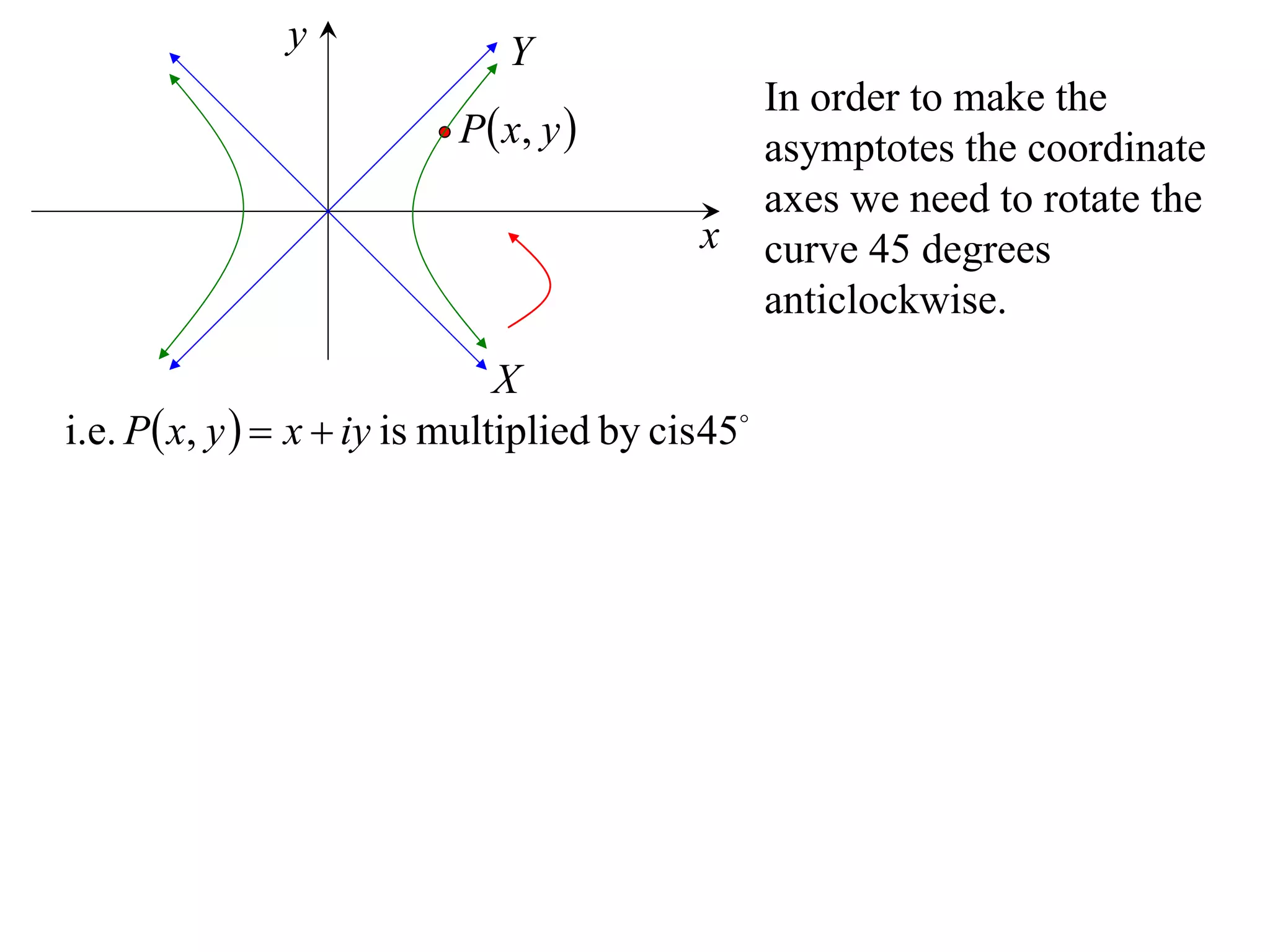
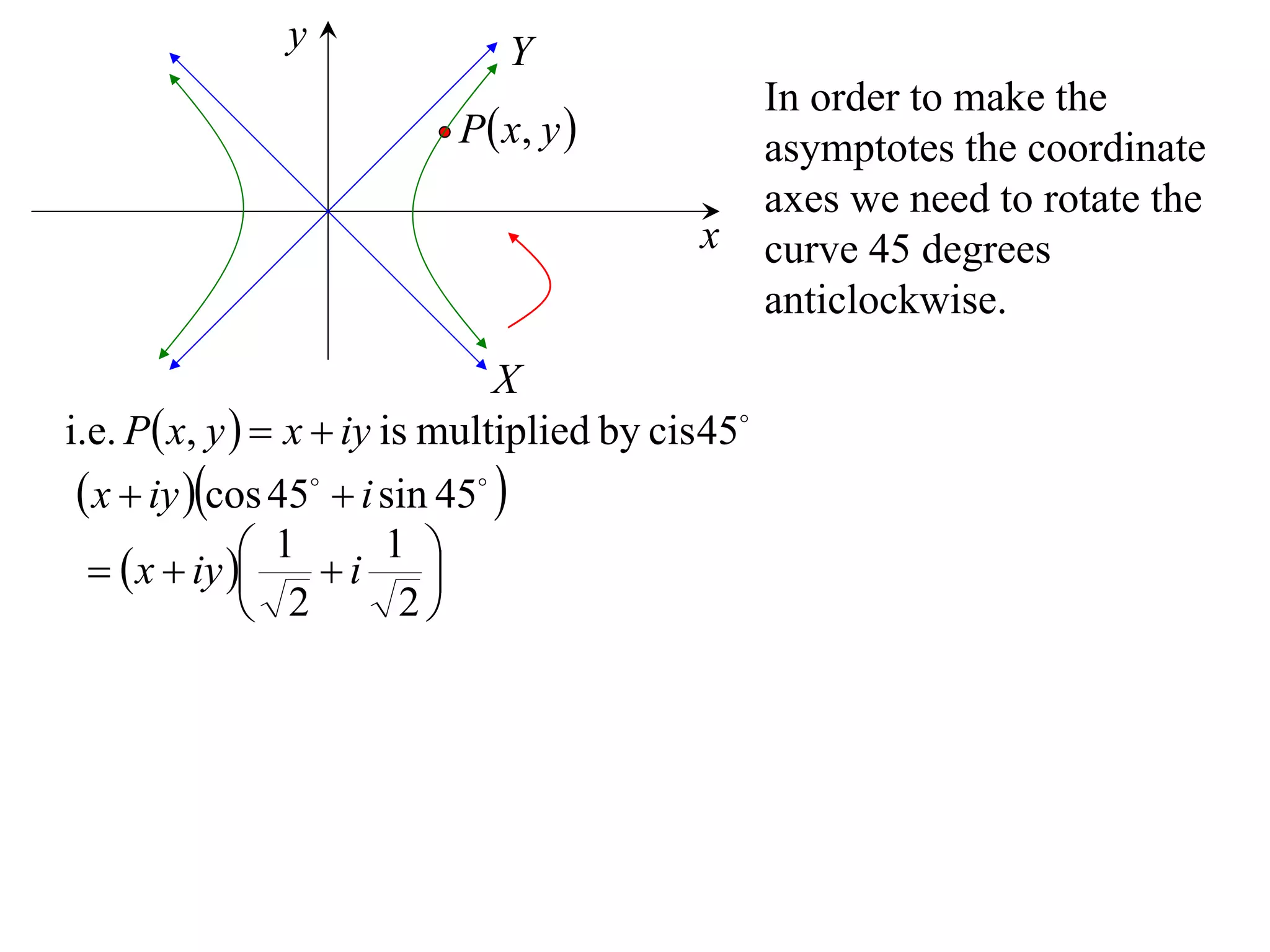
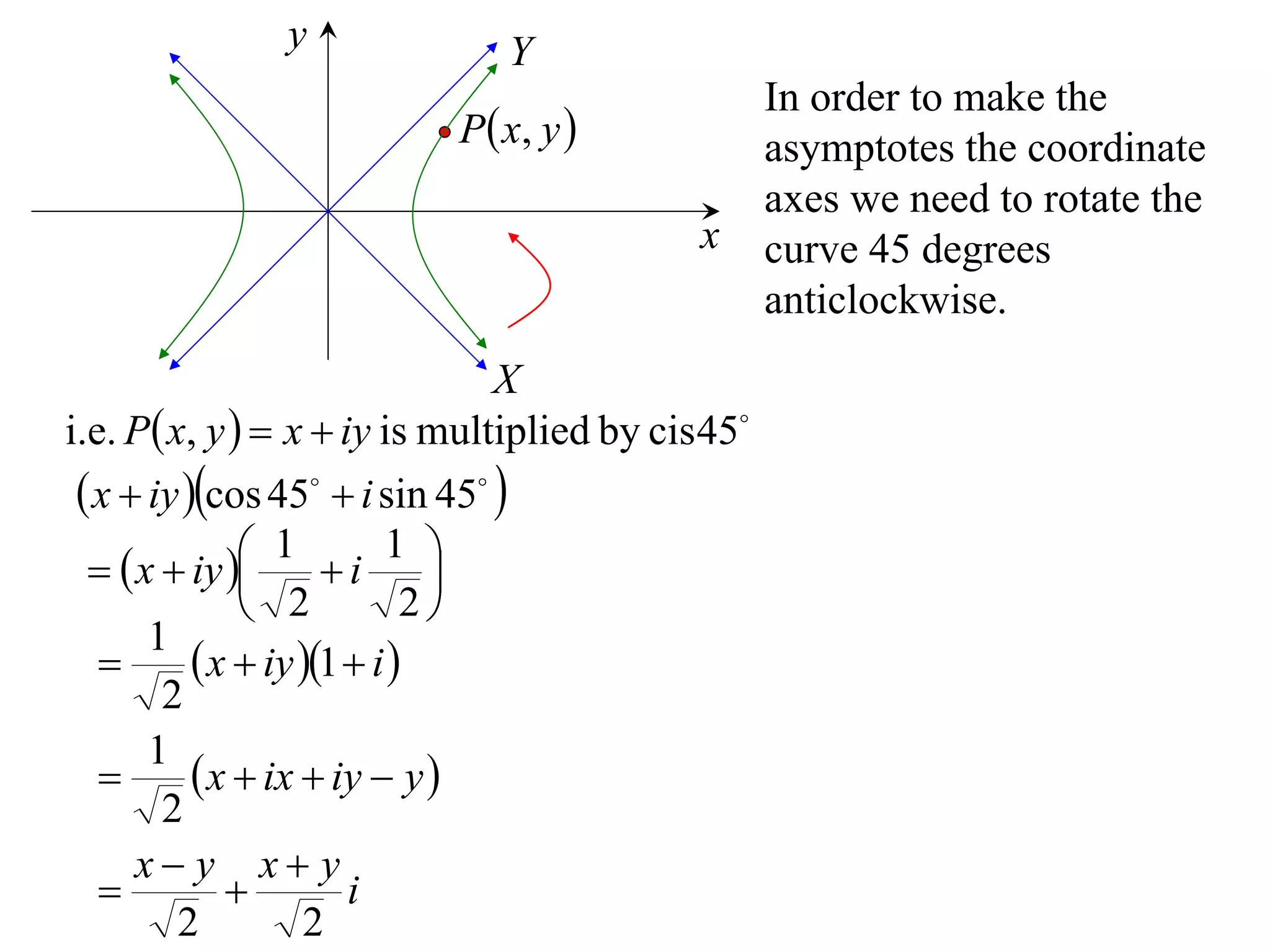
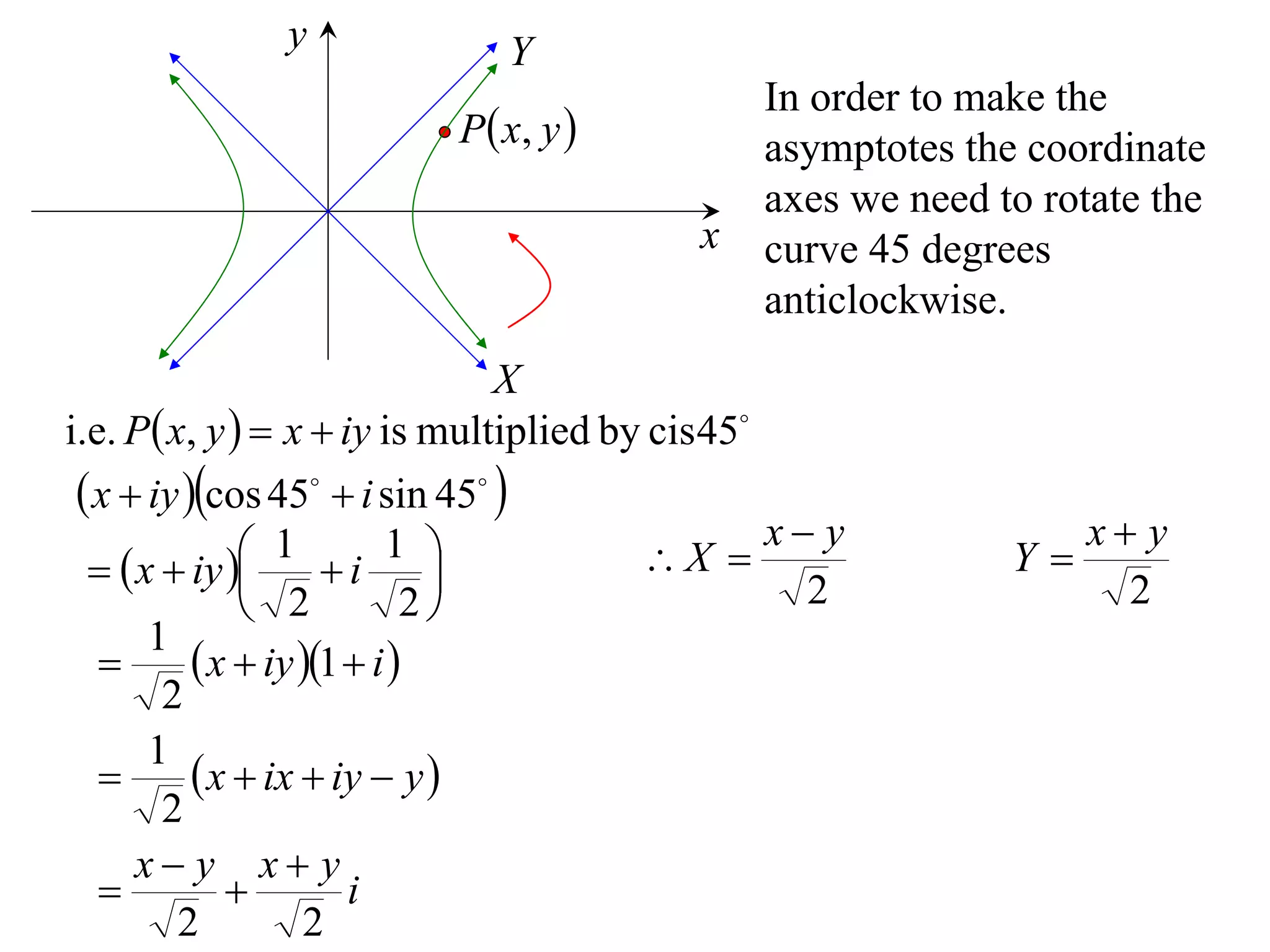
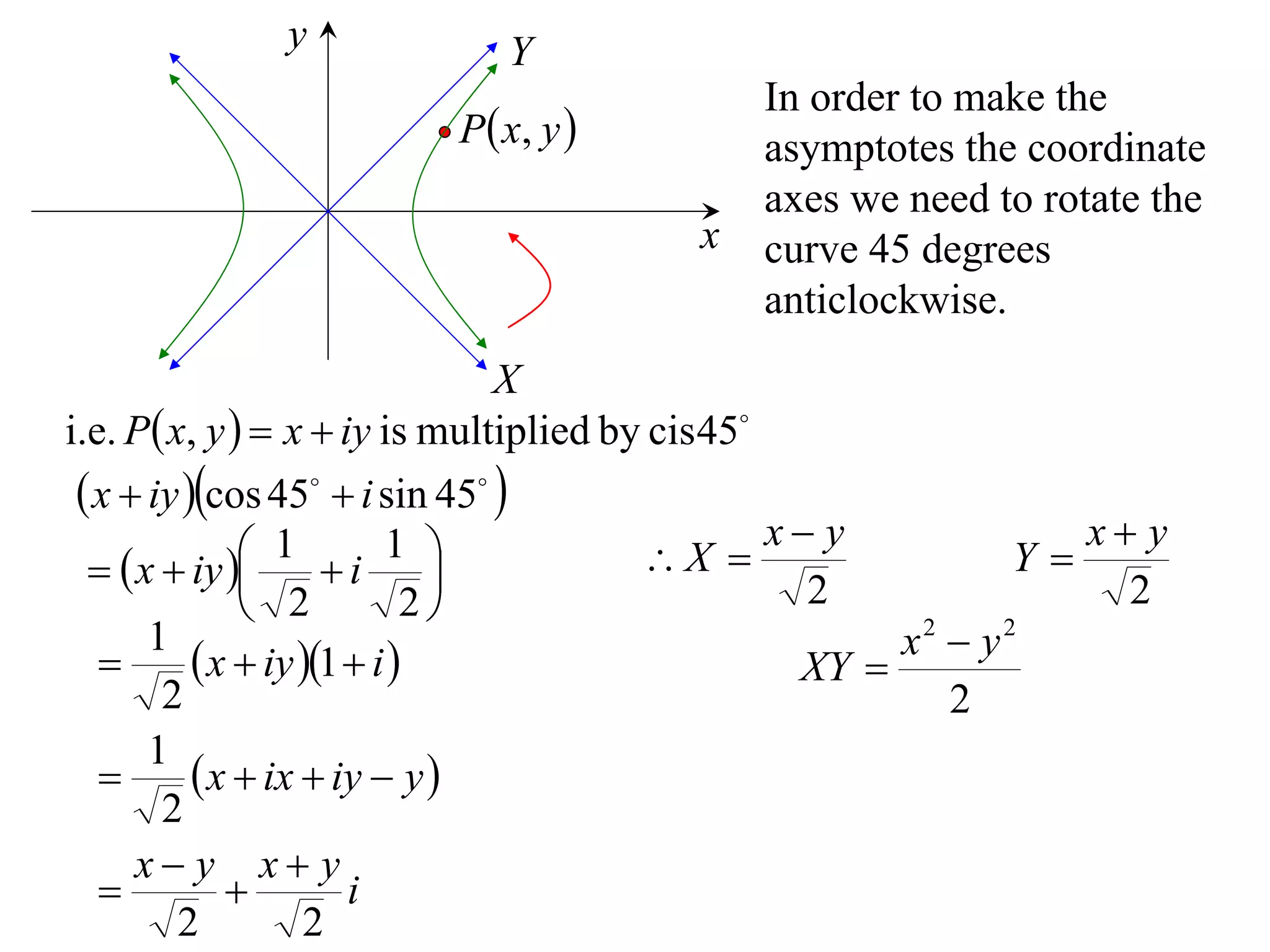
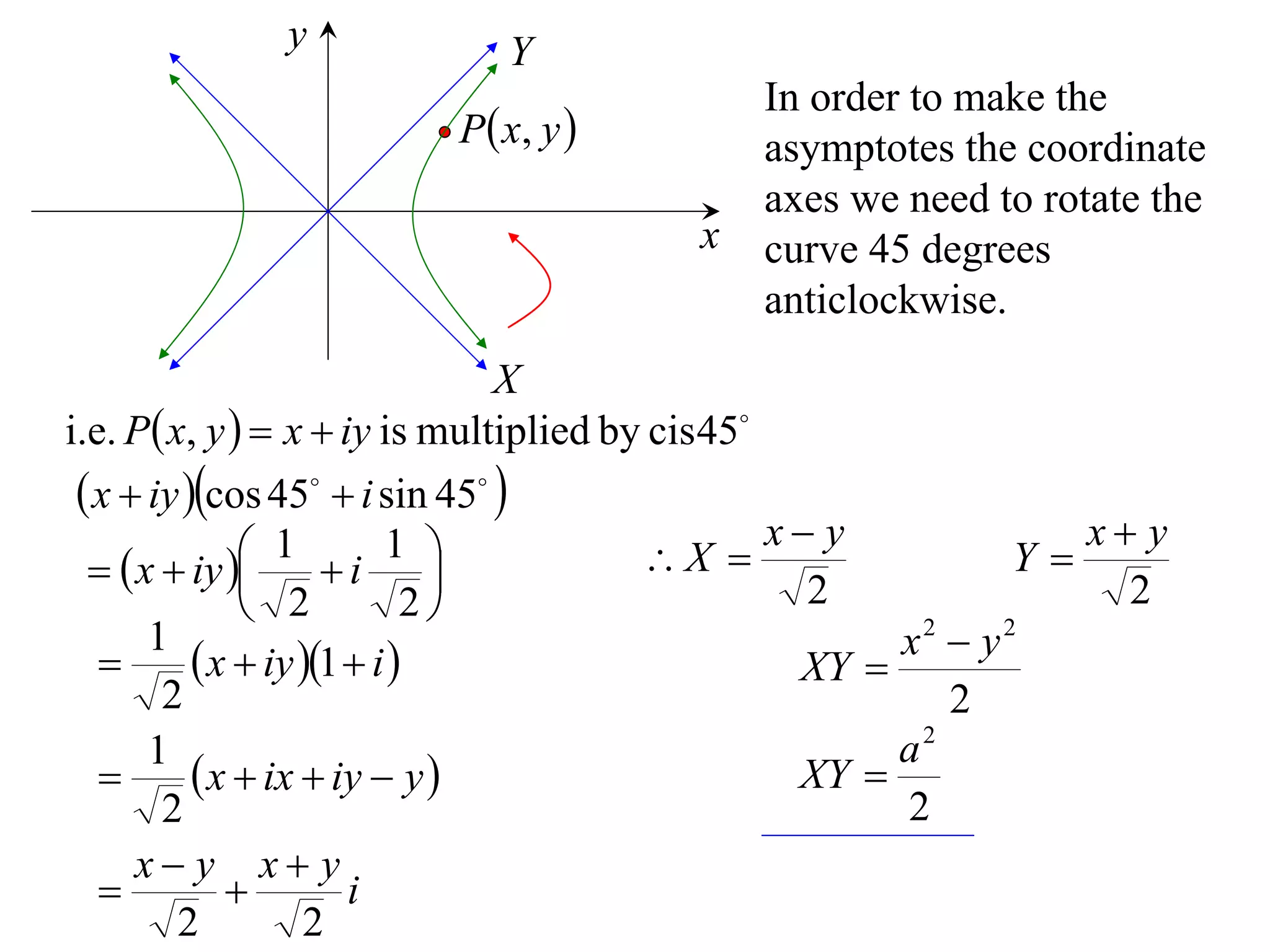
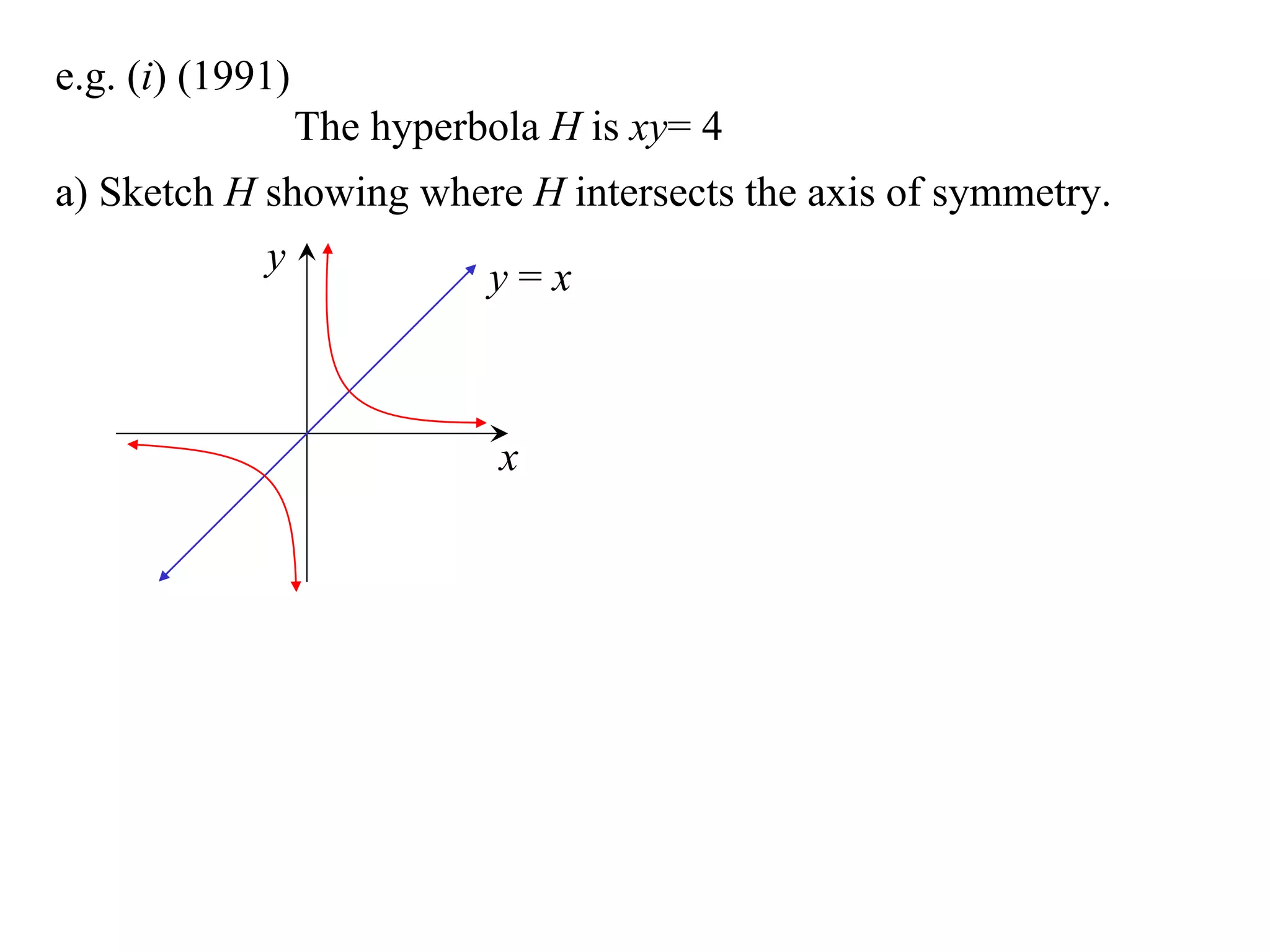
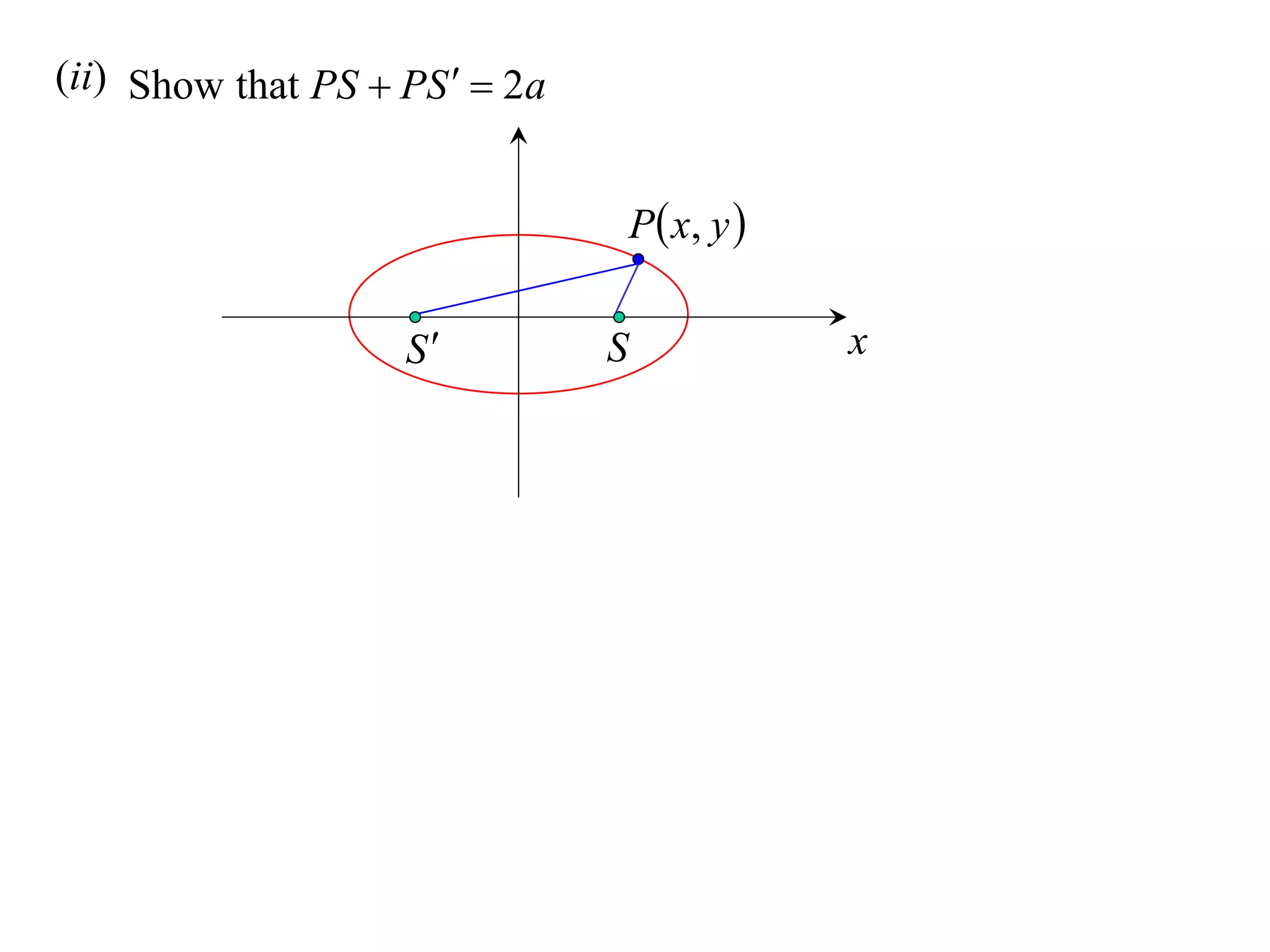
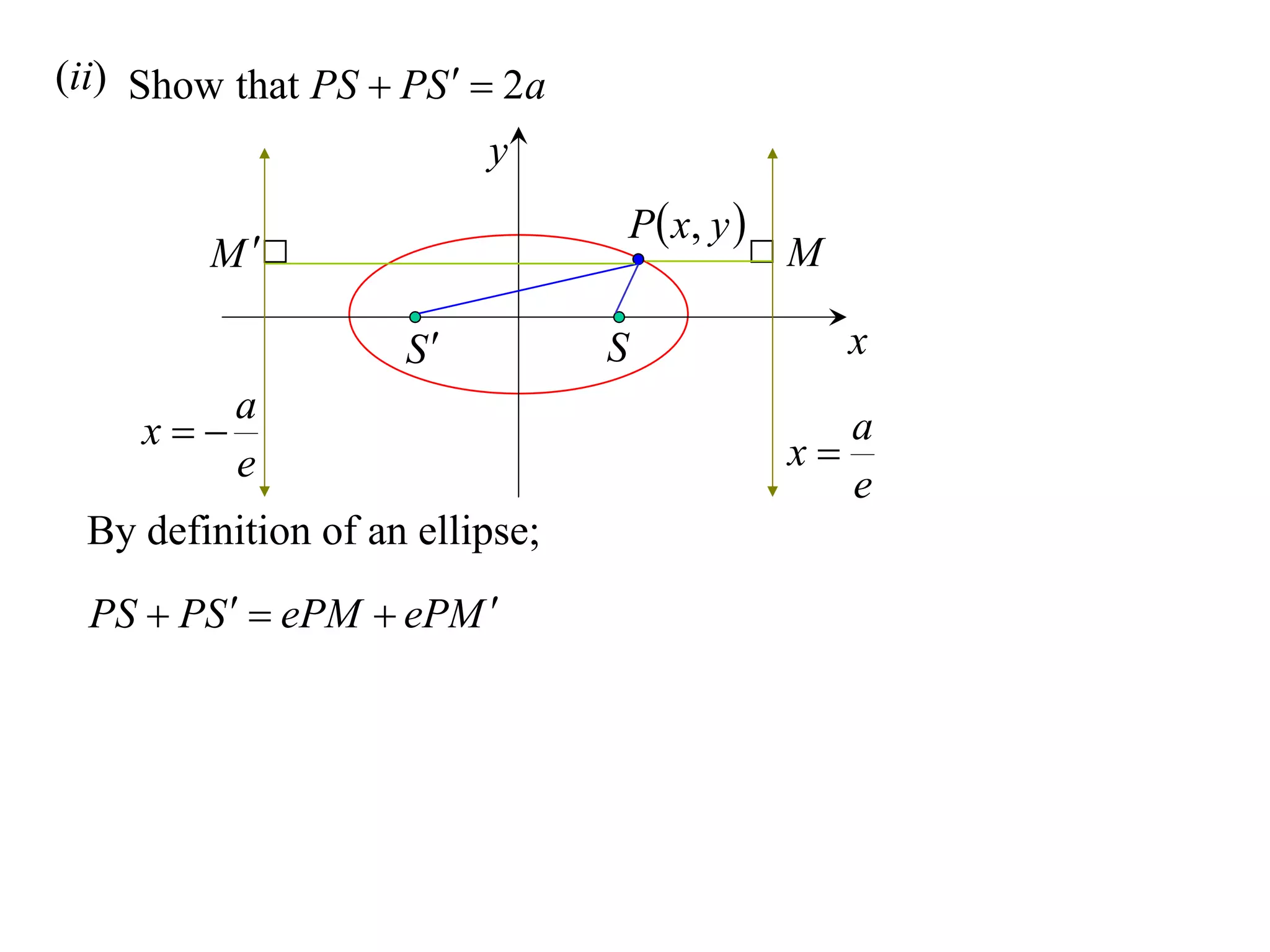
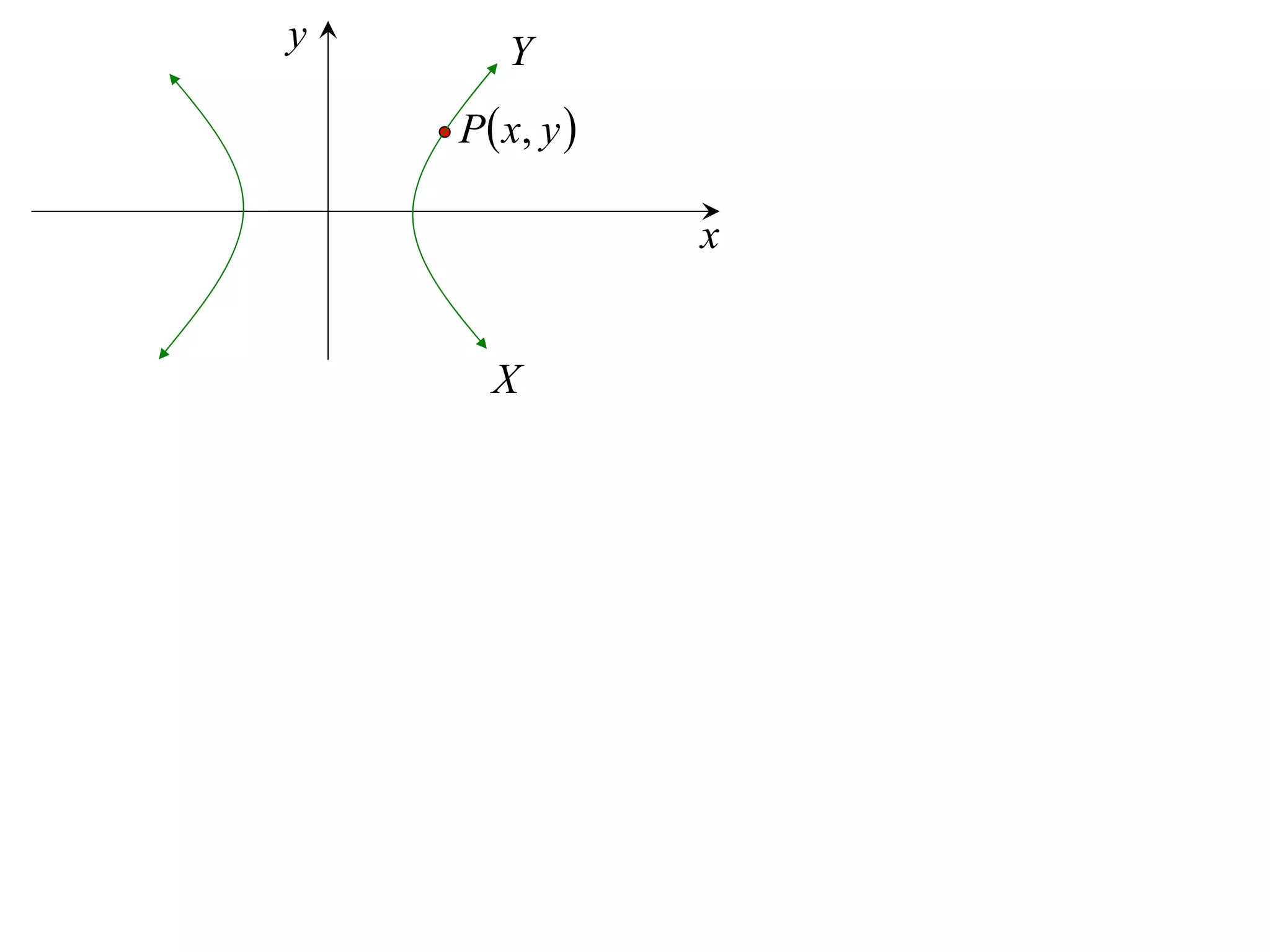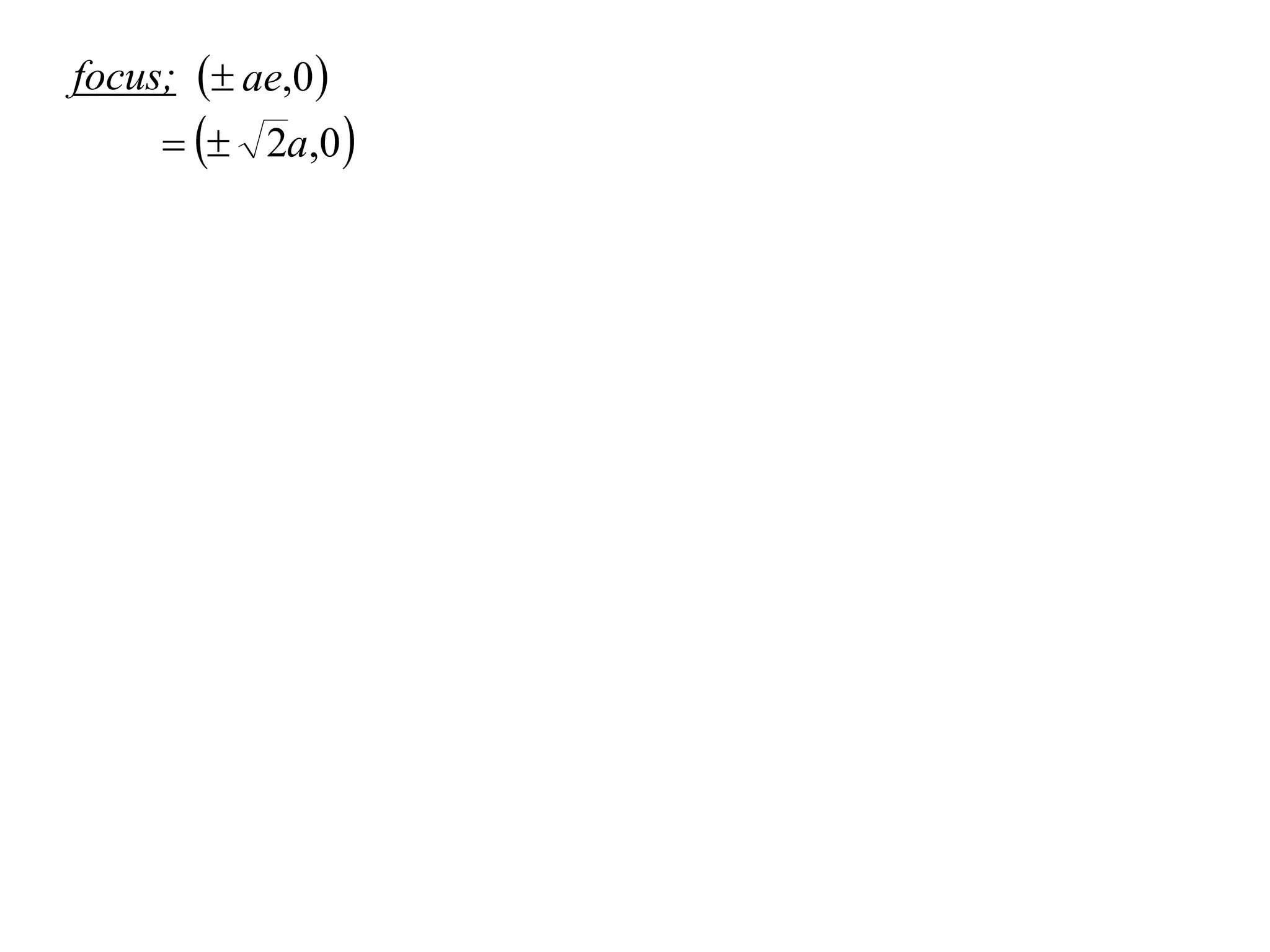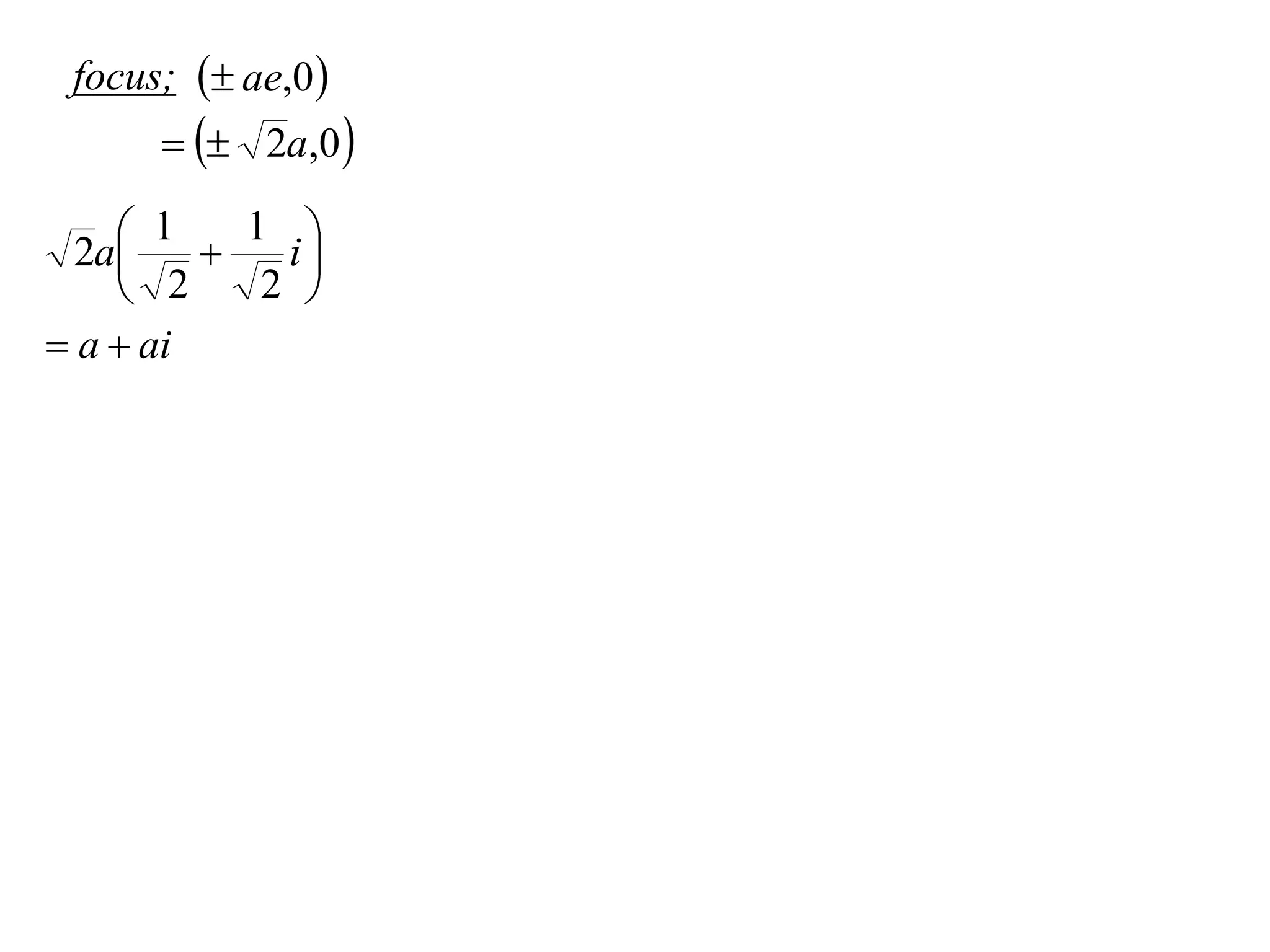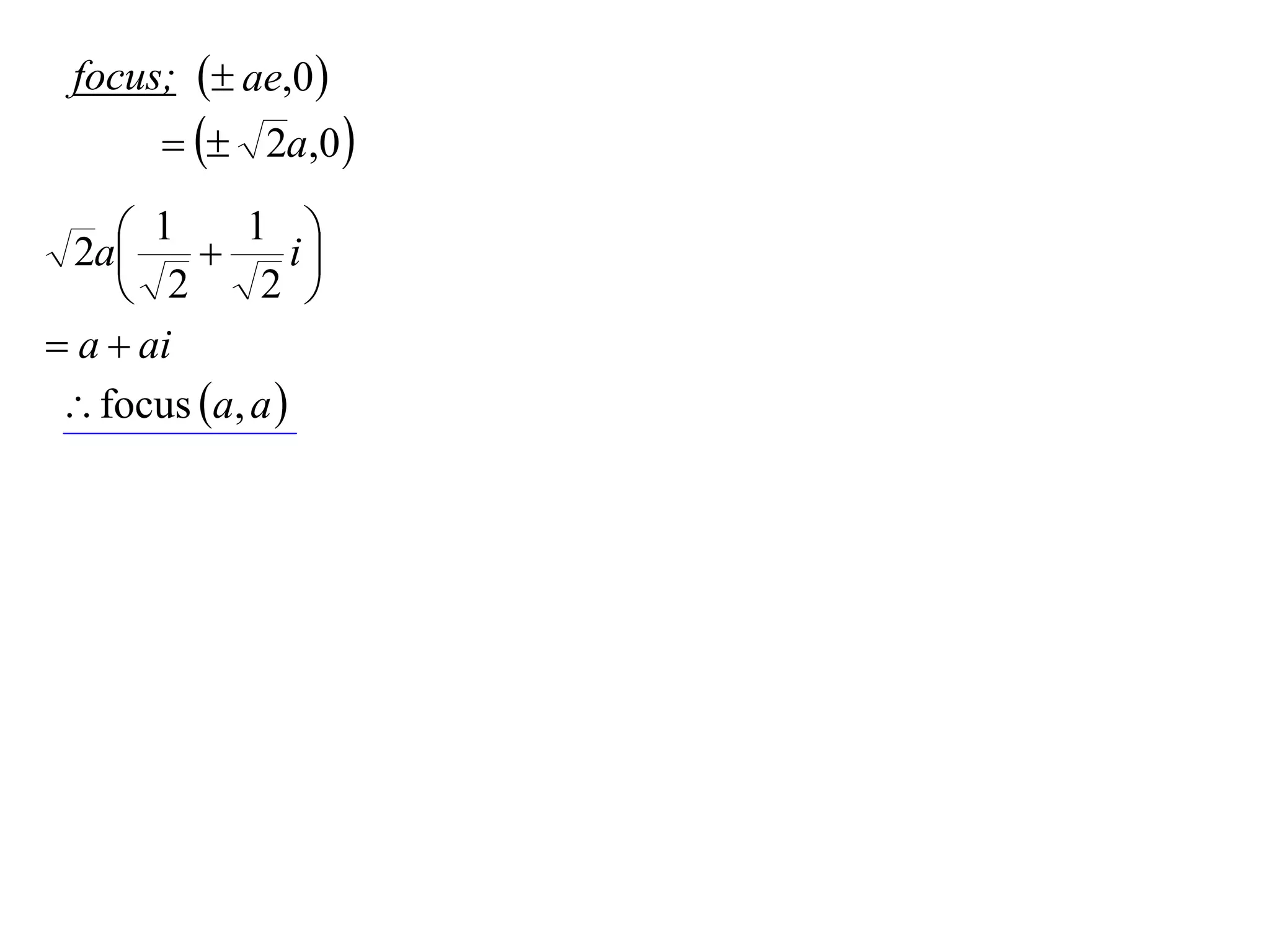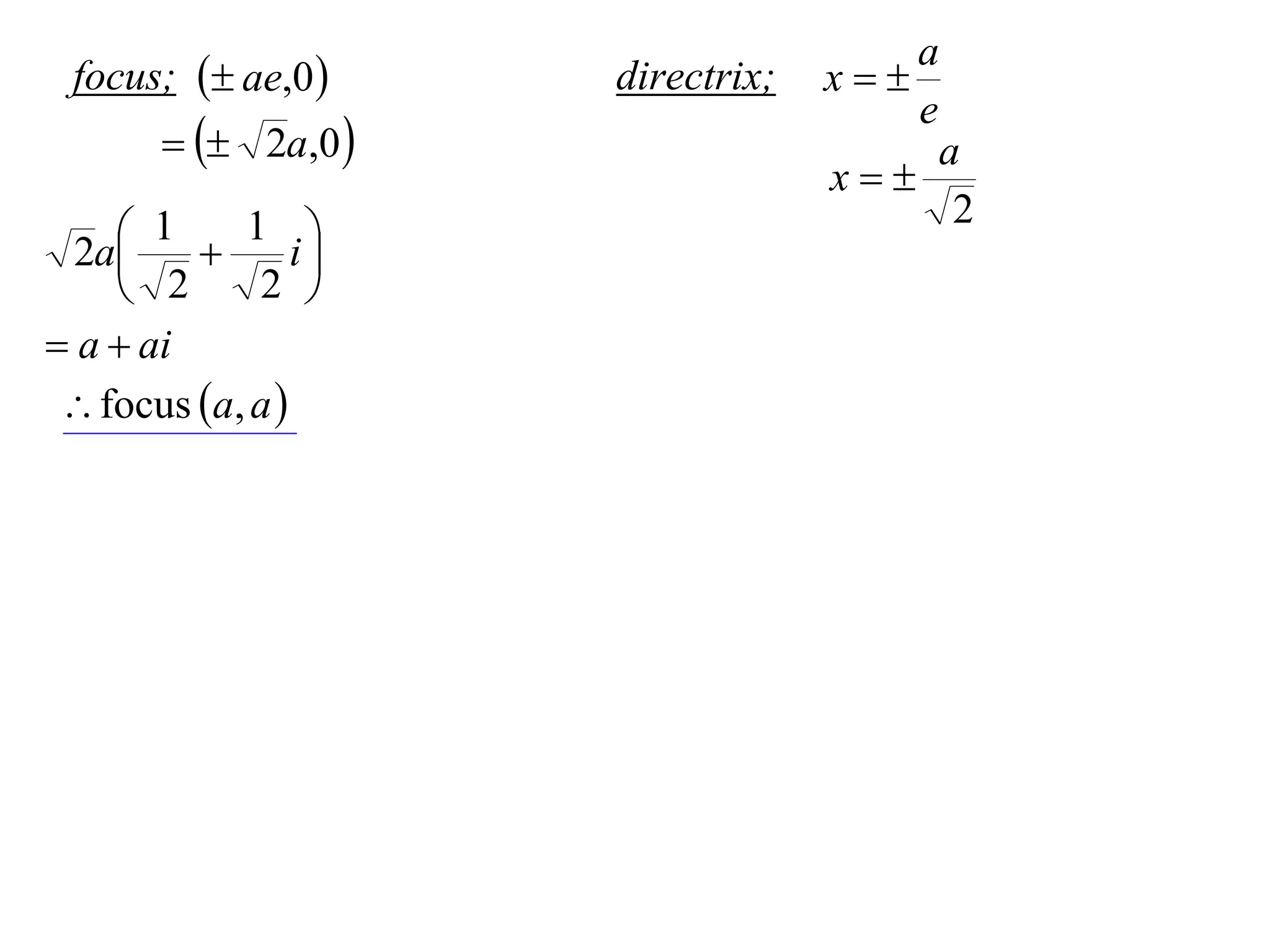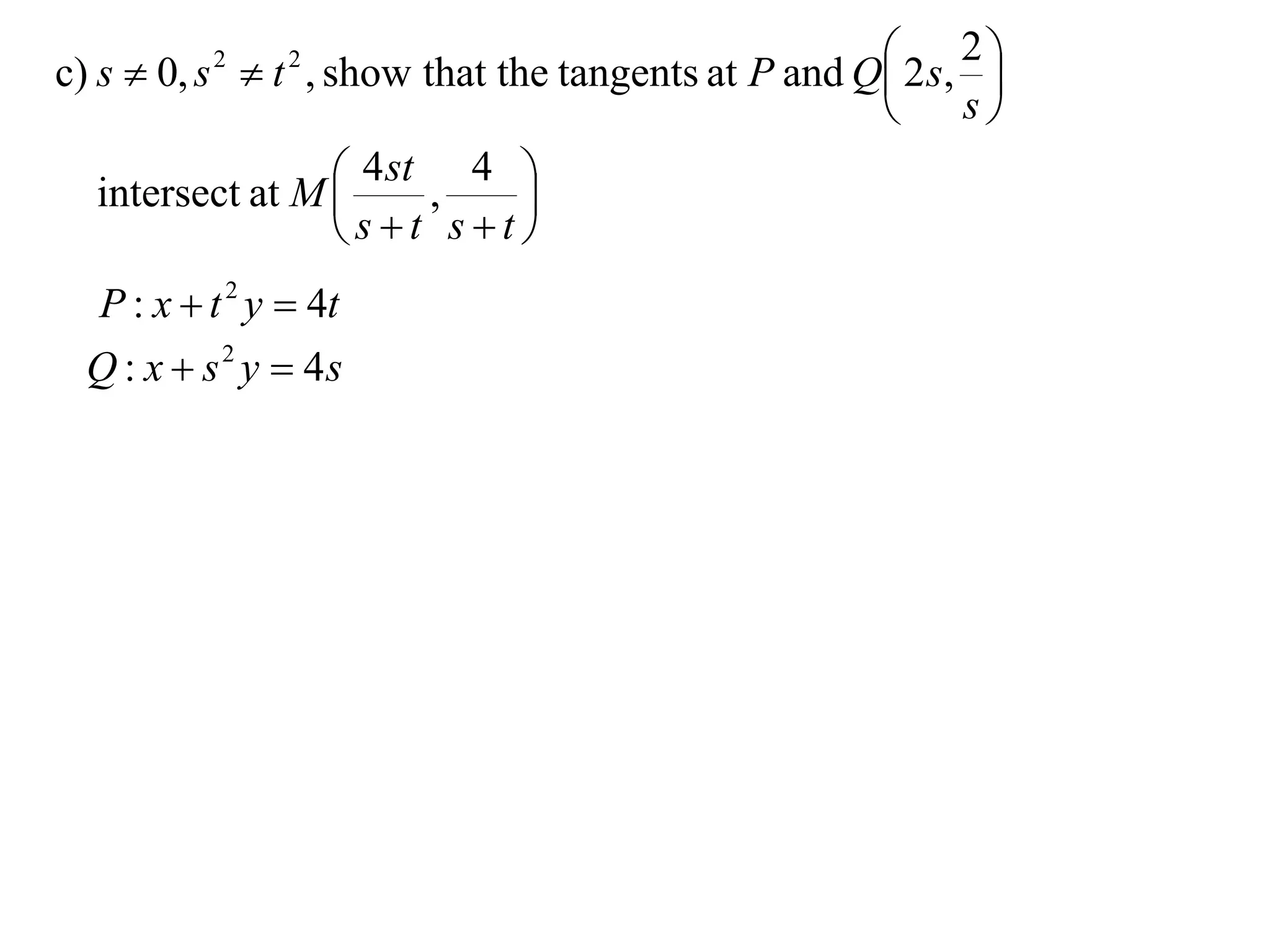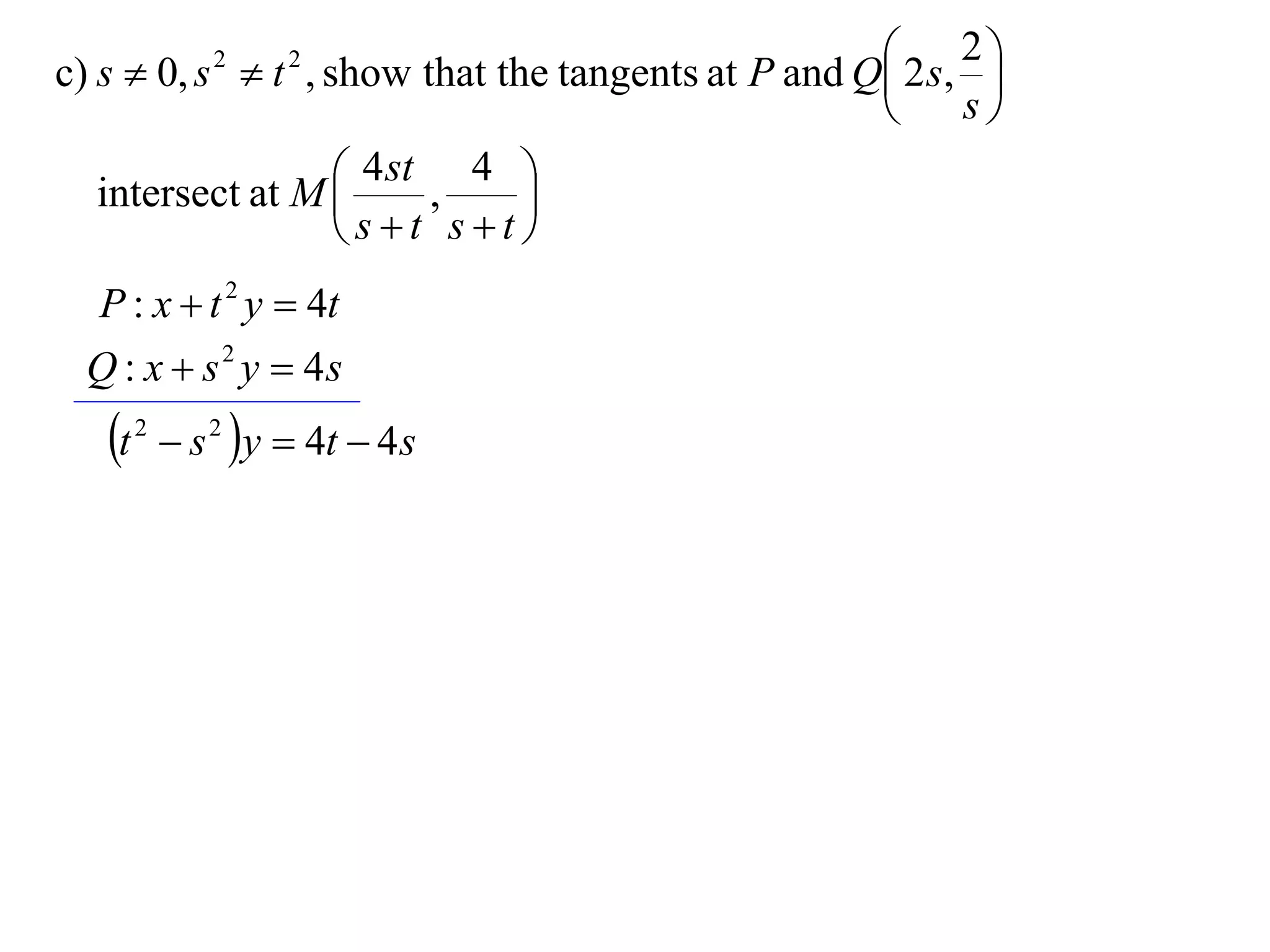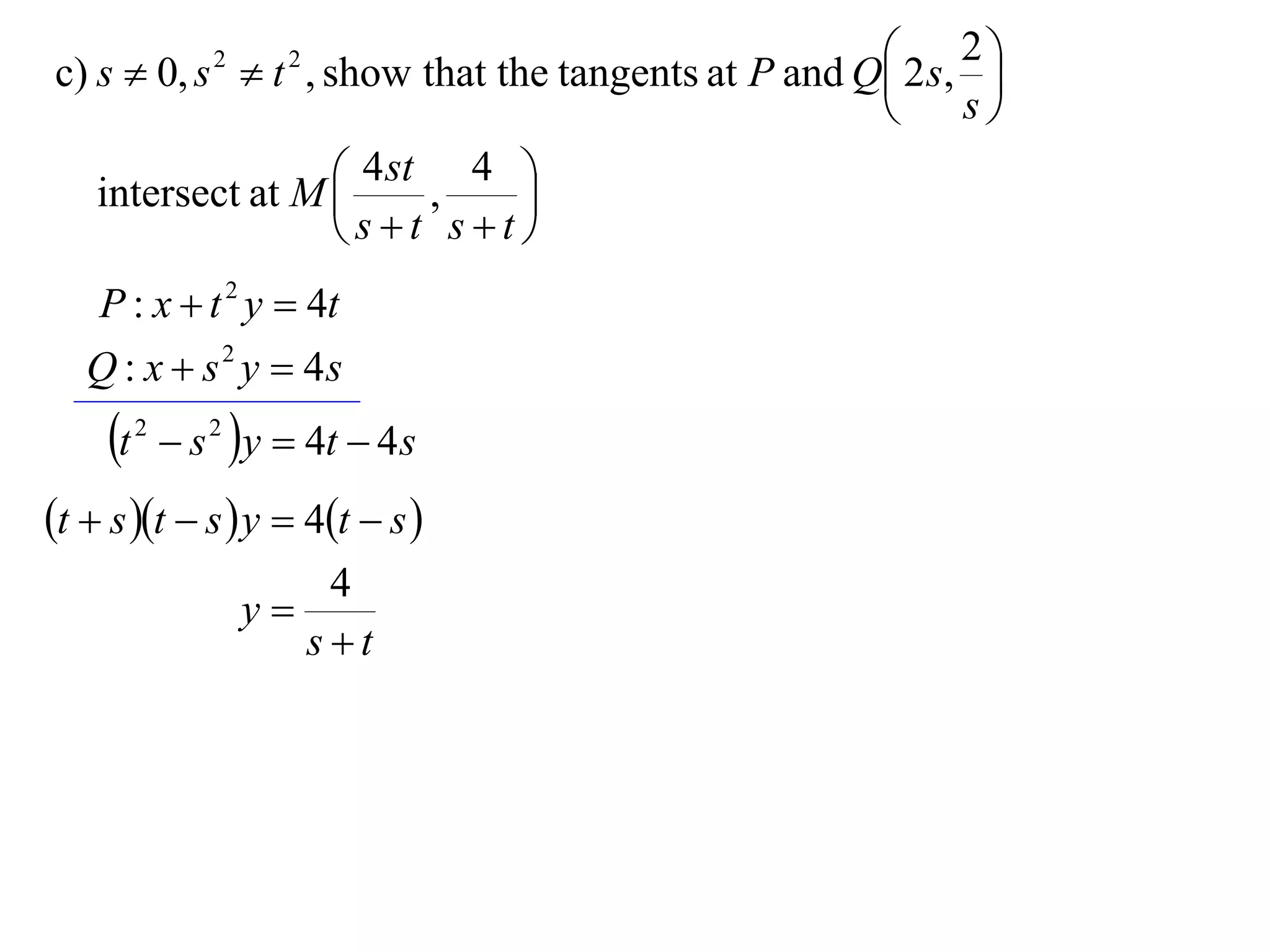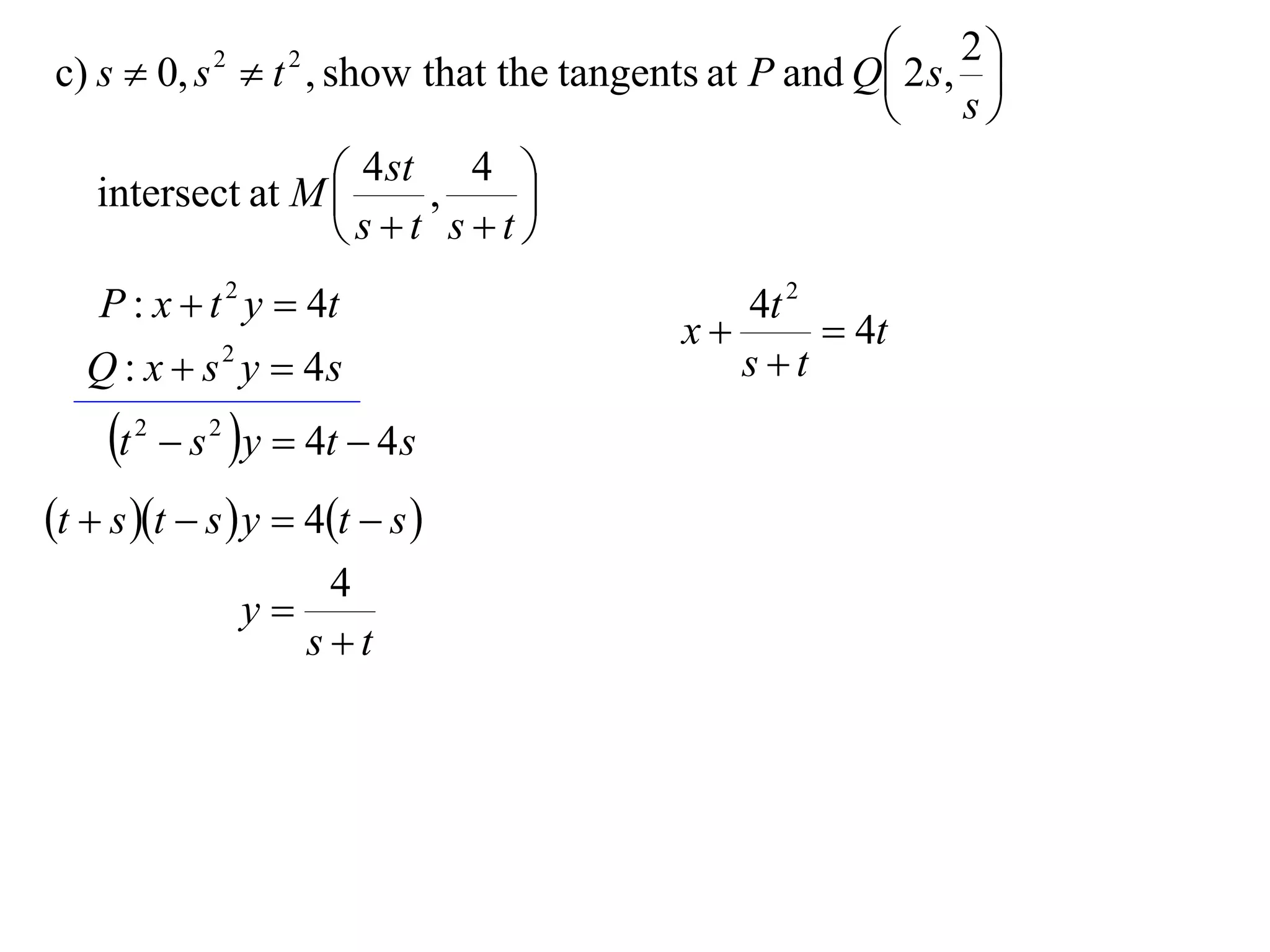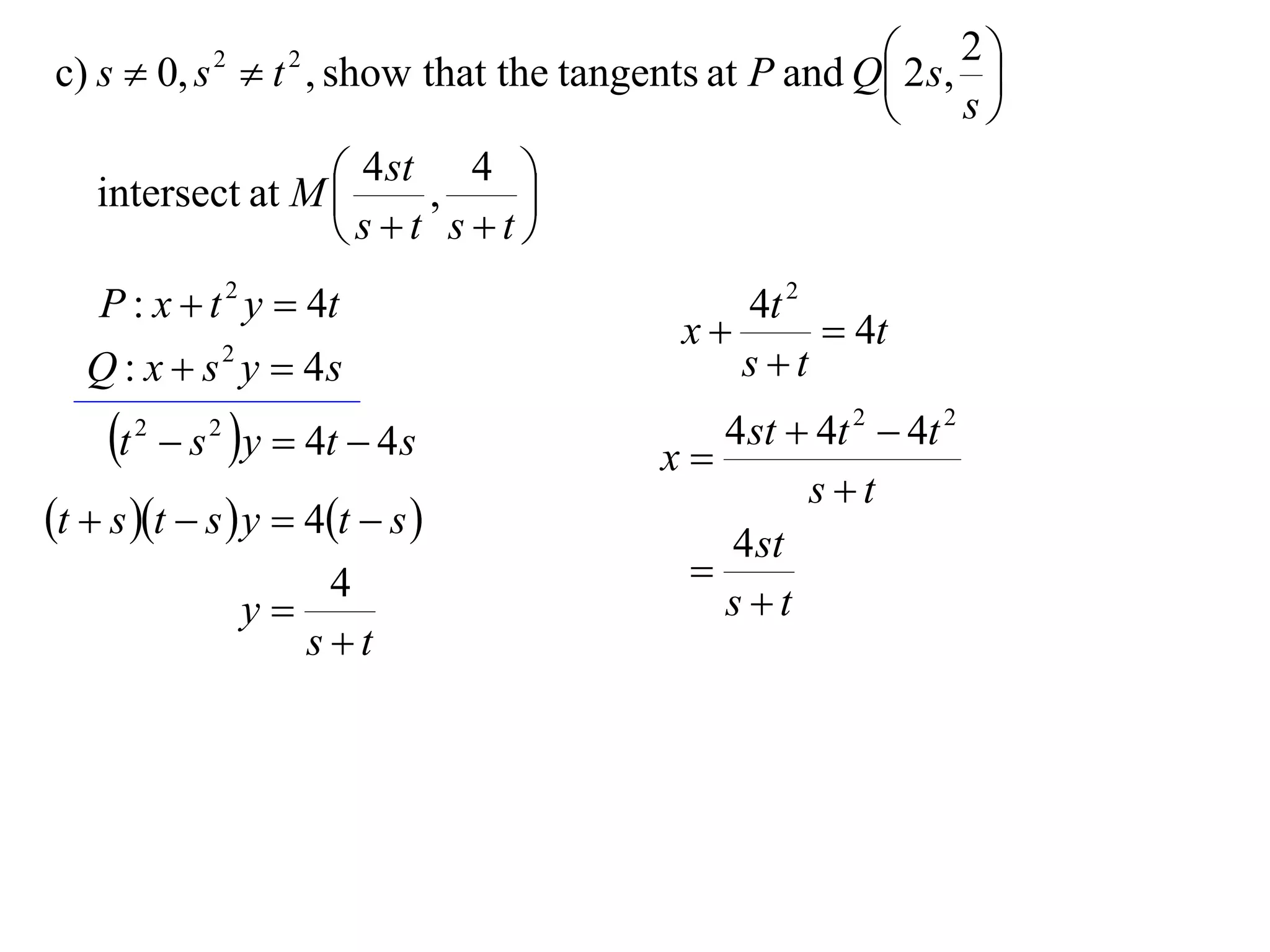A rectangular hyperbola is a hyperbola whose asymptotes are perpendicular to each other. Its equation is x2/a2 - y2/a2 = 1. Rotating the hyperbola 45 degrees anticlockwise transforms its equation to (x-y)2/a2 - (x+y)2/a2 = 1. The foci are located at (a,a) and (-a,-a). The directrices are the lines x = ±a/e, where the eccentricity e=2. The distance between the directrices is 2a.

1. Rectangular Hyperbola

2. Rectangular Hyperbola
A hyperbola whose asymptotes are perpendicular to each other

3. Rectangular Hyperbola
A hyperbola whose asymptotes are perpendicular to each other
b b
  1
a a

4. Rectangular Hyperbola
A hyperbola whose asymptotes are perpendicular to each other
b b
  1
a a
b2  a 2
ba

5. Rectangular Hyperbola
A hyperbola whose asymptotes are perpendicular to each other
b b
  1
a a
b2  a 2
ba
 hyperbola has the equation;
x2 y2
2
 2 1
a a
x2  y2  a2

6. Rectangular Hyperbola
A hyperbola whose asymptotes are perpendicular to each other
b b
  1
a a
b2  a 2
ba
 hyperbola has the equation; a 2 e 2  1  a 2
x2 y2
2
 2 1
a a
x2  y2  a2

7. Rectangular Hyperbola
A hyperbola whose asymptotes are perpendicular to each other
b b
  1
a a
b2  a 2
ba
 hyperbola has the equation; a 2 e 2  1  a 2
x2 y2 e2  1  1
2
 2 1
a a
e2  2
x2  y2  a2
e 2

8. Rectangular Hyperbola
A hyperbola whose asymptotes are perpendicular to each other
b b
  1
a a
b2  a 2
ba
 hyperbola has the equation; a 2 e 2  1  a 2
x2 y2 e2  1  1
2
 2 1
a a
e2  2
x2  y2  a2
e 2
 eccentricity is 2

9. y Y
P  x, y 
x
X

10. y Y
In order to make the
P  x, y  asymptotes the coordinate
axes we need to rotate the
x curve 45 degrees
anticlockwise.
X

11. y Y
In order to make the
P  x, y  asymptotes the coordinate
axes we need to rotate the
x curve 45 degrees
anticlockwise.
X
i.e. P x, y   x  iy is multiplied by cis 45

12. y Y
In order to make the
P  x, y  asymptotes the coordinate
axes we need to rotate the
x curve 45 degrees
anticlockwise.
X
i.e. P x, y   x  iy is multiplied by cis 45
 x  iy cos 45  i sin 45 
  x  iy 
1 1 
 i 
 2 2

13. y Y
In order to make the
P  x, y  asymptotes the coordinate
axes we need to rotate the
x curve 45 degrees
anticlockwise.
X
i.e. P x, y   x  iy is multiplied by cis 45
 x  iy cos 45  i sin 45 
  x  iy 
1 1 
 i 
 2 2
1
  x  iy 1  i 
2
1
  x  ix  iy  y 
2
x y x y
  i
2 2

14. y Y
In order to make the
P  x, y  asymptotes the coordinate
axes we need to rotate the
x curve 45 degrees
anticlockwise.
X
i.e. P x, y   x  iy is multiplied by cis 45
 x  iy cos 45  i sin 45 
 1 i 1  x y x y
  x  iy   X  Y
 2 2 2 2
1
  x  iy 1  i 
2
1
  x  ix  iy  y 
2
x y x y
  i
2 2

15. y Y
In order to make the
P  x, y  asymptotes the coordinate
axes we need to rotate the
x curve 45 degrees
anticlockwise.
X
i.e. P x, y   x  iy is multiplied by cis 45
 x  iy cos 45  i sin 45 
 1 i 1  x y x y
  x  iy   X  Y
 2 2 2 2
1 x2  y2
  x  iy 1  i  XY 
2 2
1
  x  ix  iy  y 
2
x y x y
  i
2 2

16. y Y
In order to make the
P  x, y  asymptotes the coordinate
axes we need to rotate the
x curve 45 degrees
anticlockwise.
X
i.e. P x, y   x  iy is multiplied by cis 45
 x  iy cos 45  i sin 45 
 1 i 1  x y x y
  x  iy   X  Y
 2 2 2 2
1 x2  y2
  x  iy 1  i  XY 
2 2
1 a2
  x  ix  iy  y  XY 
2 2
x y x y
  i
2 2

17. focus;  ae,0 
  2a,0 

18. focus;  ae,0 
  2a,0 
 1  1 i
2a 
 2 2 
 a  ai

19. focus;  ae,0 
  2a,0 
 1  1 i
2a 
 2 2 
 a  ai
 focus a, a 

20. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a 
 2 2 
 a  ai
 focus a, a 

21. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a  directrices are || to y axis
 2 2 
 when rotated || to y   x
 a  ai
 focus a, a 

22. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a  directrices are || to y axis
 2 2 
 when rotated || to y   x
 a  ai
thus in form x  y  k  0
 focus a, a 

23. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a  directrices are || to y axis
 2 2 
 when rotated || to y   x
 a  ai
thus in form x  y  k  0
 focus a, a  2a
Now distance between directrices is
2

24. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a  directrices are || to y axis
 2 2 
 when rotated || to y   x
 a  ai
thus in form x  y  k  0
 focus a, a  2a
Now distance between directrices is
2
a
 distance from origin to directrix is
2

25. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a  directrices are || to y axis
 2 2 
 when rotated || to y   x
 a  ai
thus in form x  y  k  0
 focus a, a  2a
Now distance between directrices is
2
a
 distance from origin to directrix is
2
00k a

2 2

26. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a  directrices are || to y axis
 2 2 
 when rotated || to y   x
 a  ai
thus in form x  y  k  0
 focus a, a  2a
Now distance between directrices is
2
a
 distance from origin to directrix is
2
00k a

2 2
k a
k  a

27. a
focus;  ae,0  directrix; x
e
  2a,0  a
x
2
 1  1 i
2a  directrices are || to y axis
 2 2 
 when rotated || to y   x
 a  ai
thus in form x  y  k  0
 focus a, a  2a
Now distance between directrices is
2
a
 distance from origin to directrix is
2
00k a

2 2
k a
k  a
 directrices are x  y   a

28. The rectangular hyperbola with x and y axes as aymptotes,
has the equation;
1 2
xy  a
2
where;
foci :  a, a 
directrices : x  y   a
eccentricity  2

29. The rectangular hyperbola with x and y axes as aymptotes,
has the equation;
1 2
xy  a
2
where;
foci :  a, a 
directrices : x  y   a
eccentricity  2
Parametric Coordinates of xy  c 2

30. The rectangular hyperbola with x and y axes as aymptotes,
has the equation;
1 2
xy  a
2
where;
foci :  a, a 
directrices : x  y   a
eccentricity  2
Parametric Coordinates of xy  c 2
c
x  ct y
t

31. The rectangular hyperbola with x and y axes as aymptotes,
has the equation;
1 2
xy  a
2
where;
foci :  a, a 
directrices : x  y   a
eccentricity  2
Parametric Coordinates of xy  c 2
c
x  ct y
t
Tangent: x  t 2 y  2ct

32. The rectangular hyperbola with x and y axes as aymptotes,
has the equation;
1 2
xy  a
2
where;
foci :  a, a 
directrices : x  y   a
eccentricity  2
Parametric Coordinates of xy  c 2
c
x  ct y
t
Tangent: x  t 2 y  2ct Normal: t 3 x  ty  ct 4  1

33. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.

34. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.
y y=x
x

35. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.
y y=x
xy  4
2,2
x2  4
x
 2,2 x  2

36. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.
y y=x
xy  4
2,2
x2  4
x
 2,2 x  2
 2t , 2  is x  t 2 y  4t
b) Show that the tangent at P 
 t

37. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.
y y=x
xy  4
2,2
x2  4
x
 2,2 x  2
 2t , 2  is x  t 2 y  4t
b) Show that the tangent at P 
 t
4
y
x
dy 4
 2
dx x

38. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.
y y=x
xy  4
2,2
x2  4
x
 2,2 x  2
 2t , 2  is x  t 2 y  4t
b) Show that the tangent at P 
 t
4 dy 4
y when x  2t ,  
x dx 2t 2
dy 4
 2 1
 2
dx x t

39. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.
y y=x
xy  4
2,2
x2  4
x
 2,2 x  2
 2t , 2  is x  t 2 y  4t
b) Show that the tangent at P 
 t
4 dy 4 2 1
y when x  2t ,   y    2  x  2t 
x dx 2t 2
t t
dy 4
 2 1
 2
dx x t

40. e.g. (i) (1991)
The hyperbola H is xy= 4
a) Sketch H showing where H intersects the axis of symmetry.
y y=x
xy  4
2,2
x2  4
x
 2,2 x  2
 2t , 2  is x  t 2 y  4t
b) Show that the tangent at P 
 t
4 dy 4 2 1
y when x  2t ,   y    2  x  2t 
x dx 2t 2
t t
dy 4 1 t 2 y  2t   x  2t
 2  2
dx x t x  t 2 y  4t

41.  2 s, 2 
c) s  0, s  t , show that the tangents at P and Q
2 2

 s
intersect at M  4 st , 4 

 st st

42.  2 s, 2 
c) s  0, s  t , show that the tangents at P and Q
2 2

 s
intersect at M  4 st , 4 

 st st
P : x  t 2 y  4t
Q : x  s 2 y  4s

43.  2 s, 2 
c) s  0, s  t , show that the tangents at P and Q
2 2

 s
intersect at M  4 st , 4 

 st st
P : x  t 2 y  4t
Q : x  s 2 y  4s
t 2
 s 2 y  4t  4 s

44.  2 s, 2 
c) s  0, s  t , show that the tangents at P and Q
2 2

 s
intersect at M  4 st , 4 

 st st
P : x  t 2 y  4t
Q : x  s 2 y  4s
t 2
 s 2 y  4t  4 s
t  s t  s  y  4t  s 
4
y
st

45.  2 s, 2 
c) s  0, s  t , show that the tangents at P and Q
2 2

 s
intersect at M  4 st , 4 

 st st
P : x  t 2 y  4t 4t 2
x  4t
Q : x  s 2 y  4s st
t 2
 s 2 y  4t  4 s
t  s t  s  y  4t  s 
4
y
st

46.  2 s, 2 
c) s  0, s  t , show that the tangents at P and Q
2 2

 s
intersect at M  4 st , 4 

 st st
P : x  t 2 y  4t 4t 2
x  4t
Q : x  s 2 y  4s st
t 2
 s y  4t  4 s
2
x
4 st  4t 2  4t 2
st
t  s t  s  y  4t  s  4 st
4 
y st
st

47.  2 s, 2 
c) s  0, s  t , show that the tangents at P and Q 
2 2
 s
intersect at M  4 st , 4 

 st st
P : x  t 2 y  4t 4t 2
x  4t
Q : x  s 2 y  4s st
t 2
 s y  4t  4 s
2
x
4 st  4t 2  4t 2
st
t  s t  s  y  4t  s  4 st
4 
y st
st
 4 st , 4 
 M is  
 st st

48. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.

49. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.
4 st 4
x y
st st

50. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.
4 st 4
x y
st st
1
s
t
st  1

51. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.
4 st 4
x y
st st
1
s
t
st  1
4
x
st

52. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.
4 st 4
x y
st st
1
s
t
st  1
4 y
4
x
st st
 x

53. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.
4 st 4
x y
st st
1
s
t
st  1
4 y
4
x
st st
 x
 y  x

54. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.
4 st 4
x y
st st
1
s
t
st  1
4 y
4
x
st st
 x
4
 y  x  0, thus M  0,0 
st

55. 1
d) Suppose that s  , show that the locus of M is a straight
t
line through the origin, but not including the origin.
4 st 4
x y
st st
1
s
t
st  1
4 y
4
x
st st
 x
4
 y  x  0, thus M  0,0 
st
 locus of M is y   x, excluding 0,0 

56. (ii) Show that PS  PS   2a
P  x, y 
S S x

57. (ii) Show that PS  PS   2a
y
P  x, y 
S S x
By definition of an ellipse;

58. (ii) Show that PS  PS   2a
y
P  x, y 
M
S S x
a
x x
a
e e
By definition of an ellipse;
PS  PS   ePM

59. (ii) Show that PS  PS   2a
y
P  x, y 
M M
S S x
a
x x
a
e e
By definition of an ellipse;
PS  PS   ePM  ePM 

60. (ii) Show that PS  PS   2a
y
P  x, y 
M M
S S x
a
x x
a
e e
By definition of an ellipse;
PS  PS   ePM  ePM 
 e PM  PM 
 2a 
 e 
 e 
 2a

61. (ii) Show that PS  PS   2a
y
P  x, y 
M M
S S x
a
x x
a
e e
By definition of an ellipse;
PS  PS   ePM  ePM 
 e PM  PM  Exercise 6D; 3, 4, 7, 10, 11a,
 2a 
 e 
12, 14, 19, 21, 26, 29,
 e  31, 43, 47
 2a