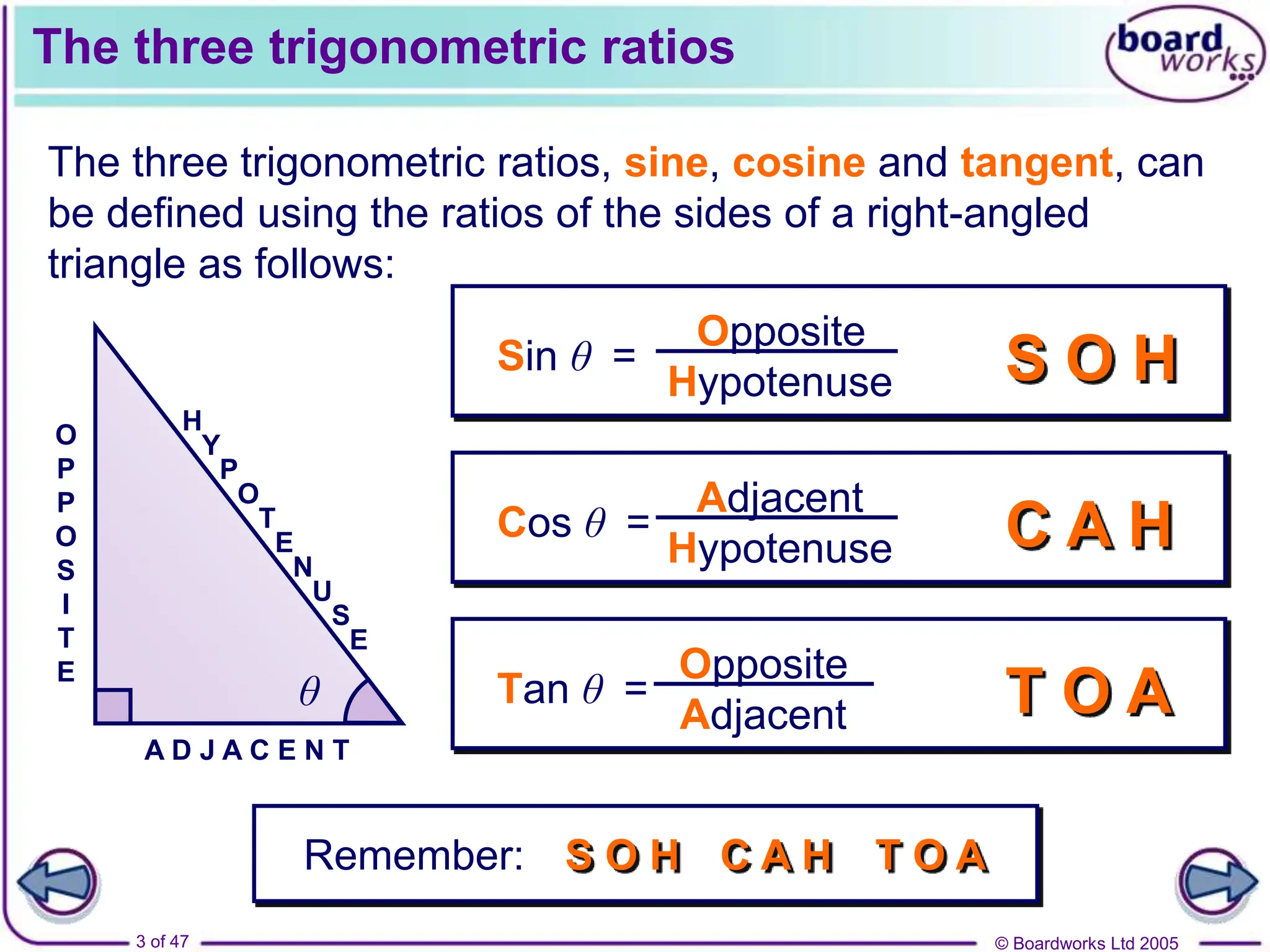
This document provides information on trigonometric functions including:
- Definitions of sine, cosine, and tangent ratios using right triangles and unit circles.
- Graphs of y=sinθ, y=cosθ, and y=tanθ showing their periodic and other key properties.
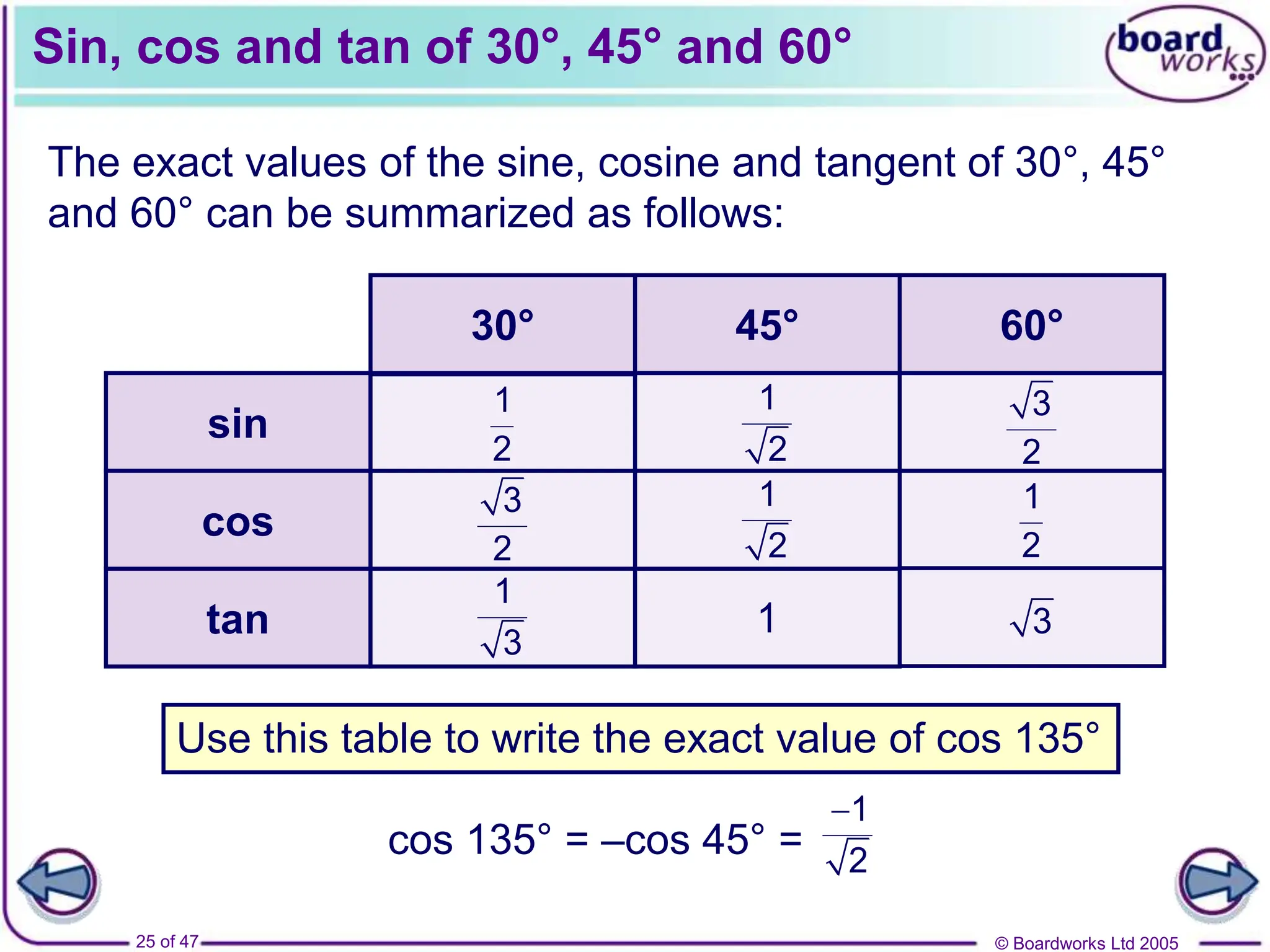
- Exact values of trig functions for common angles like 30°, 45°, 60° using example right triangles.
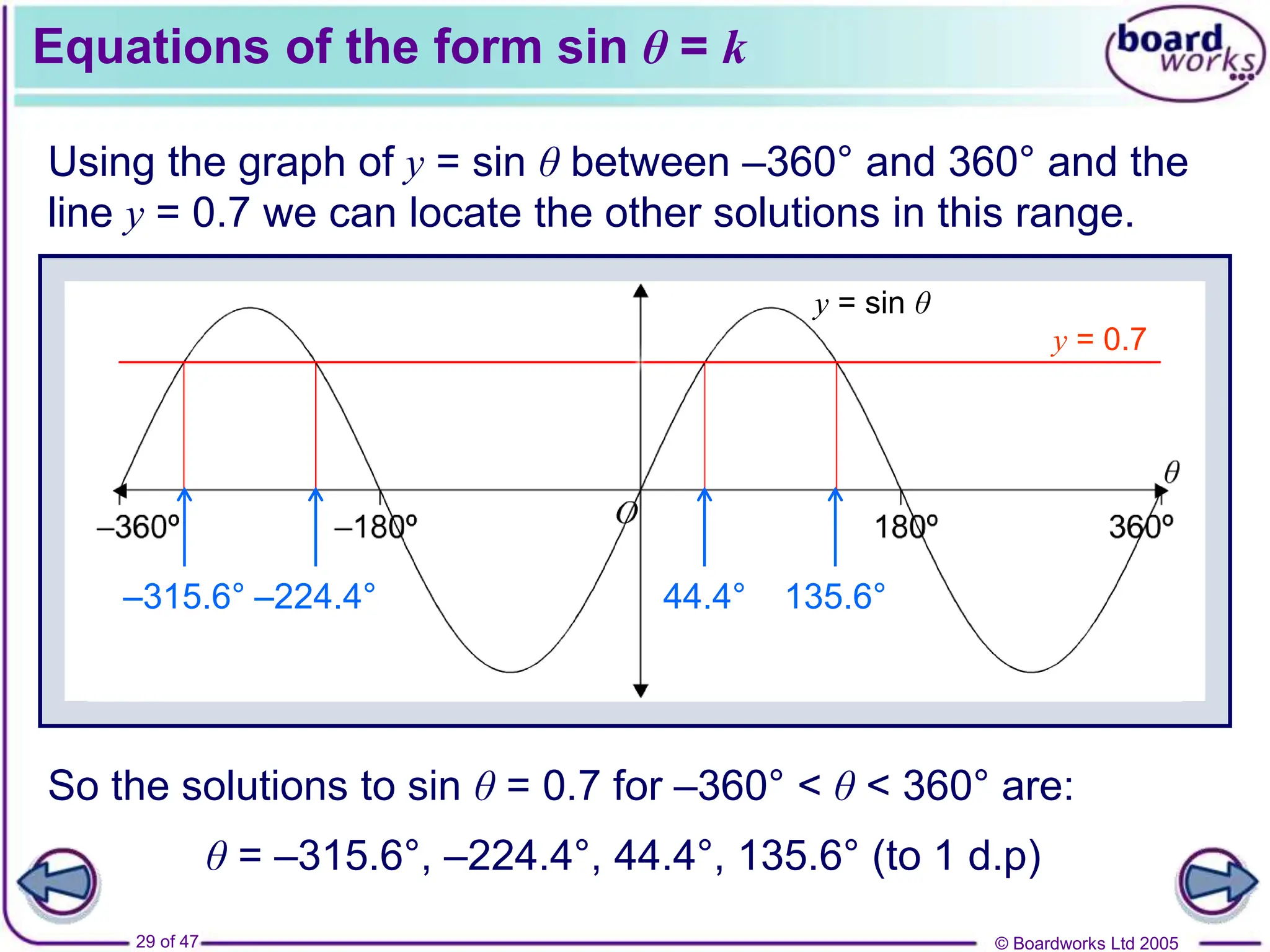
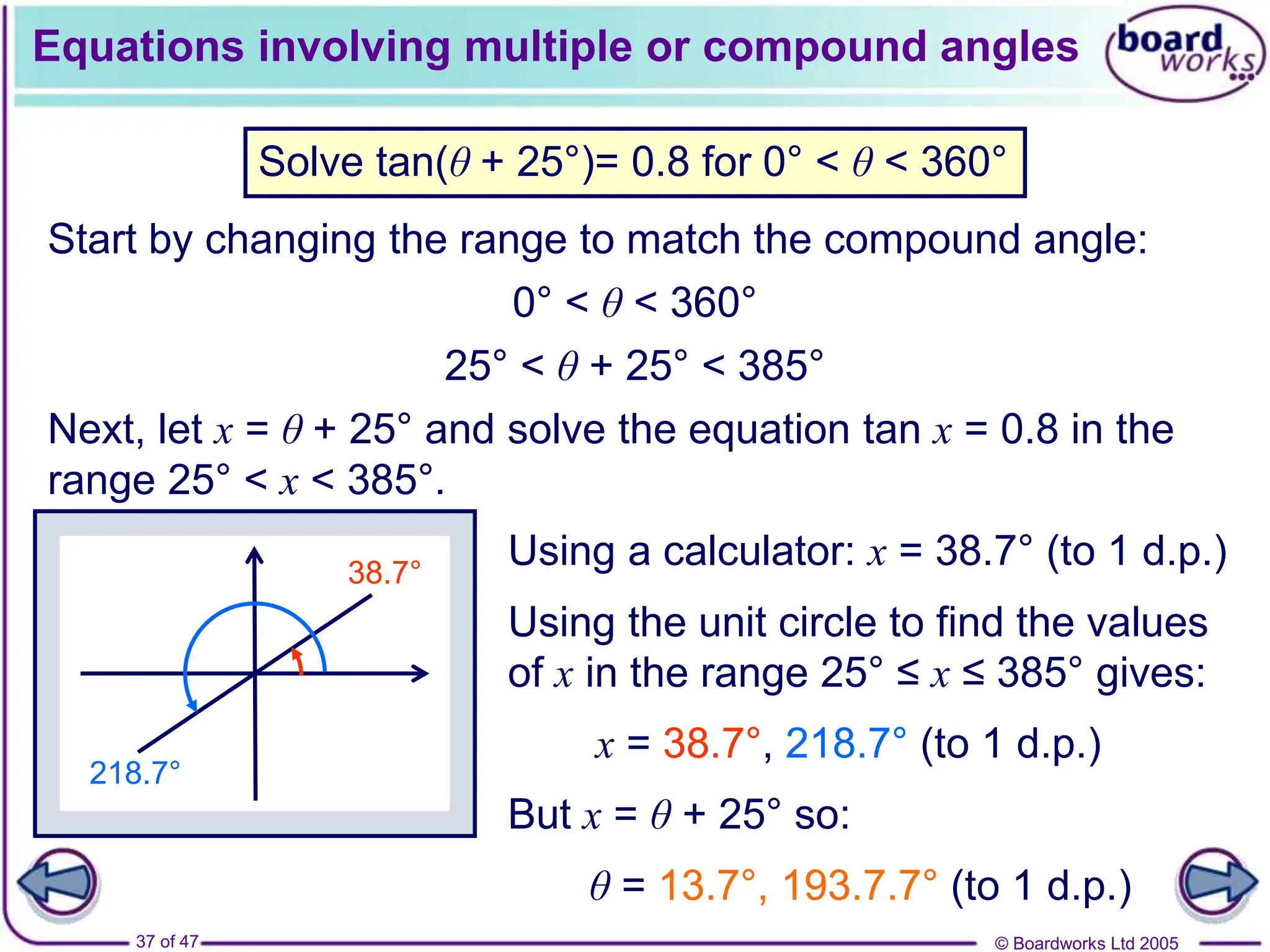
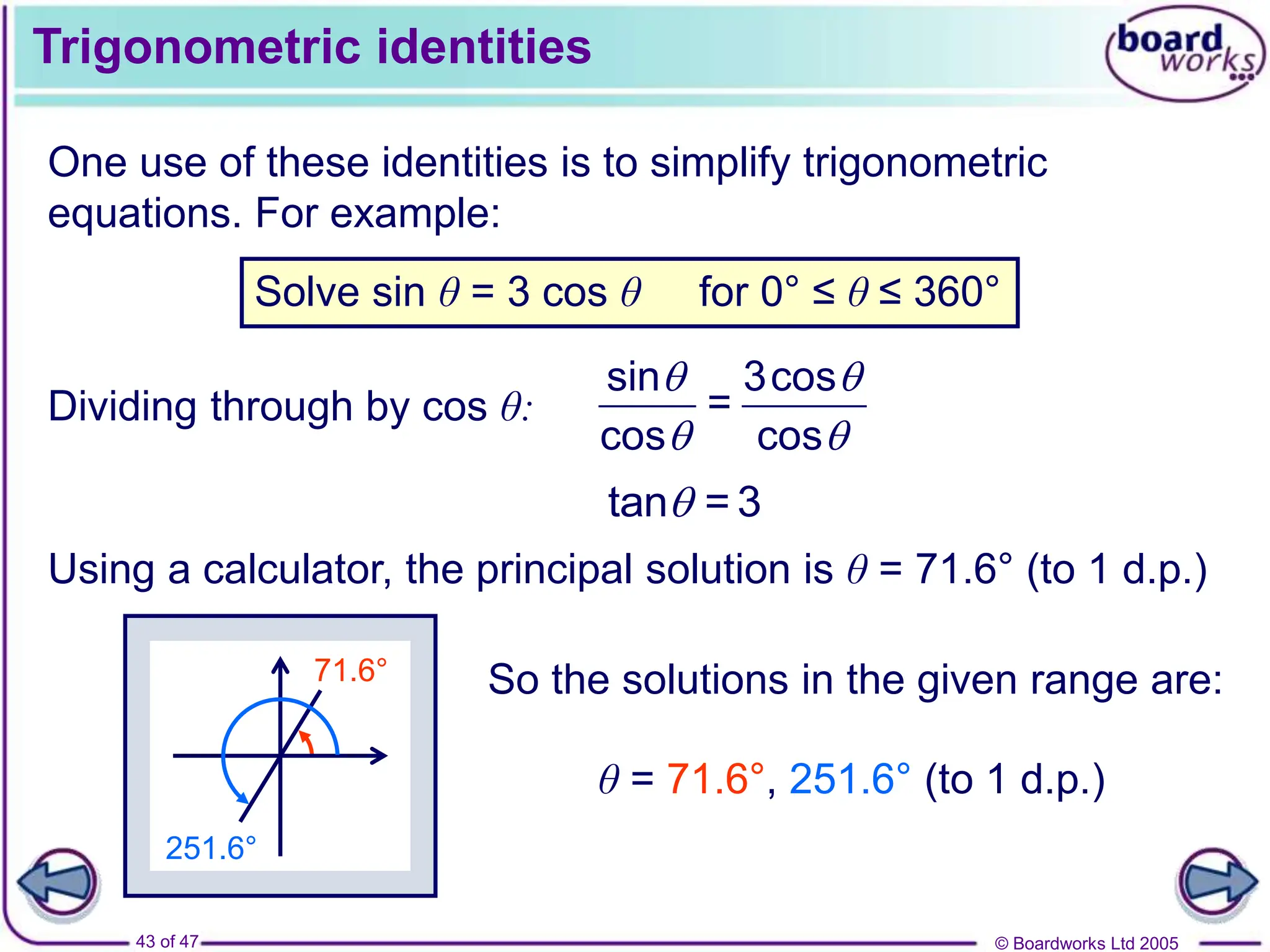
- How to solve trigonometric equations like sinθ=k that have multiple solutions over different angle ranges.