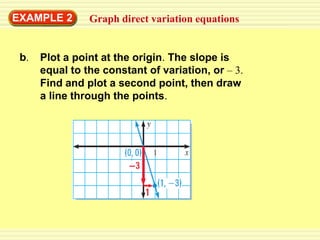
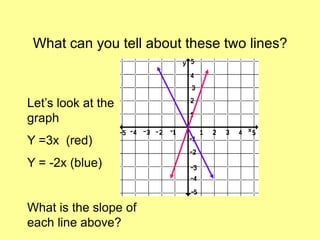
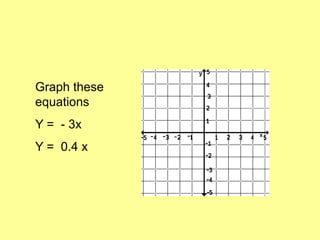
The document discusses direct variation, which is a relationship where two quantities vary proportionally such that their ratio remains constant. The key points are: 1) A direct variation relationship can be expressed as y = ax, where a is the constant of variation. 2) For a relationship to be direct variation, the equation must be able to be rewritten in the form y = ax. 3) A direct variation equation will result in a line passing through the origin when graphed.

1. Direct Variation
Section 4.6
Page 253

2. • When x and y vary directly, there is a
nonzero number a such that the following
is true:
y = ax
a is the constant of variation
For example: y = 3x or y = -1/4x
non-example : y = 4x + 5

3. • y = ax shows direct variation
between x & y
• What else is true about this type of
equation?
• YES = it goes through the origin!

4. EXAMPLE 1 Identify direct variation equations
Tell whether the equation represents direct variation.
If so, identify the constant of variation.
a. 2x – 3y = 0 b. – x + y = 4

5. EXAMPLE 1 Identify direct variation equations
SOLUTION
To tell whether an equation represents direct
variation, try to rewrite the equation in the form y = ax.
2x – 3y = 0 Write original equation.
– 3y = – 2x Subtract 2x from each side.
2x Simplify.
y= 3
ANSWER
Because the equation 2x – 3y = 0 can be
rewritten in the form y = ax, it represents direct
variation. The constant of variation is. 2
3

6. EXAMPLE 1 Identify direct variation equations
b. –x+y=4 Write original equation.
y = x+4 Add x to each side.
ANSWER
Because the equation – x + y = 4 cannot be
rewritten in the form y = ax, it does not represent
direct variation.

7. EXAMPLE 2 Graph direct variation equations
Graph the direct variation equation.
2
a. y = x b. y = – 3x
3
SOLUTION
a. Plot a point at the origin.
The slope is equal to the
constant of variation, or 2
Find and plot a second 3
point, then draw a line
through the points.

8. EXAMPLE 2 Graph direct variation equations
b. Plot a point at the origin. The slope is
equal to the constant of variation, or – 3.
Find and plot a second point, then draw
a line through the points.

9. What can you tell about these two lines?
Let’s look at the
graph
Y =3x (red)
Y = -2x (blue)
What is the slope of
each line above?

10. Graph these
equations
Y = - 3x
Y = 0.4 x

11. EXAMPLE 3 Write and use a direct variation equation
The graph of a direct variation
equation is shown.
a. Write the direct variation equation.
b. Find the value of y when x = 30.
SOLUTION
a. Because y varies directly with x, the equation
has the form y = ax. Use the fact that y = 2 when
x = – 1 to find a.
y = ax Write direct variation equation.
2 = a (– 1) Substitute.
–2=a Solve for a.

12. • Assignment:
• P. 256 (#1-15, 19-20)
• You will need graph paper