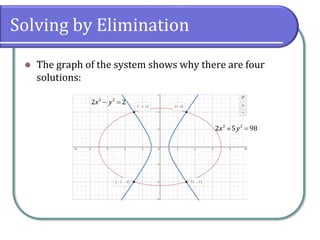
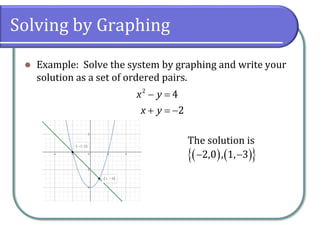
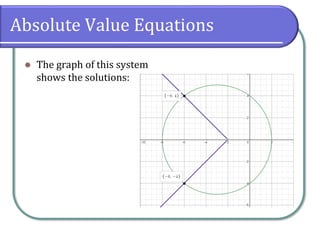
This document discusses methods for solving nonlinear systems of equations, including elimination, substitution, and graphing. It provides examples of solving systems by each method and writing the solutions as ordered pairs. Nonlinear systems contain at least one equation that is not linear. Elimination transforms equations so variables can be eliminated. Substitution solves one equation for a variable and substitutes into the other equations. Graphing can also show the intersection points that are the solutions. The document emphasizes being able to use any solving method and explains solutions may be irrational numbers. It concludes with assigning practice problems from the textbook.

1. 9.5 Nonlinear Systems
Chapter 9 Systems and Matrices

2. Concepts and Objectives
⚫ Solve nonlinear systems by
⚫ Elimination
⚫ Substitution
⚫ Graphing

3. Nonlinear Systems
⚫ A nonlinear system is one in which at least one equation
is not linear.
⚫ You can solve a nonlinear system by
⚫ Elimination – transform one or both equations so that
you can eliminate one of the variables by combining
the equations together
⚫ Substitution – solve one equation for one variable
and substitute it into the other equation(s)
⚫ Graphing (sometimes)

4. Solving by Elimination
⚫ Example: Solve the system and write your solution as a
set of ordered pairs.
 + =

− =
2 2
2 2
2 5 98
2 2
x y
x y

5. Solving by Elimination
⚫ Example: Solve the system and write your solution as a
set of ordered pairs.
Because the coefficients of x are the same, this is a good
candidate for elimination. To solve, multiply the second
equation by ‒1 and combine the two equations.
 + =

− =
2 2
2 2
2 5 98
2 2
x y
x y

6. Solving by Elimination
⚫ Example: Solve the system and write your solution as a
set of ordered pairs.
Now plug in y in one of the equations and solve for x.
 + =

− =
2 2
2 2
2 5 98
2 2
x y
x y
+ =
− + = −
2 2
2 2
2 5 98
2 2
x y
x y ‒1
=2
6 96y
=2
16y
= 4y

7. Solving by Elimination
⚫ Example: Solve the system and write your solution as a
set of ordered pairs.
− =2
2 16 2x (we already know y2 = 16)
=2
2 18x
=2
9x
= 3x
( ) ( ) ( ) ( ) − − − −3,4 , 3, 4 , 3,4 , 3, 4

8. Solving by Elimination
⚫ The graph of the system shows why there are four
solutions:
+ =2 2
2 5 98x y
− =2 2
2 2x y

9. Solving by Substitution
⚫ Example: Solve by substitution and write the solution as
a set of ordered pairs.
 + =

− = −
2 2
25
5
x y
y x

10. Solving by Substitution
⚫ Example: Solve by substitution and write the solution as
a set of ordered pairs.
Solve the second equation for y and substitute into the
first equation:
 + =

− = −
2 2
25
5
x y
y x
−= 5y x ( ) =−+
22
55 2xx

11. Solving by Substitution
⚫ Example: Solve by substitution and write the solution as
a set of ordered pairs.
Plug each value of x back in and solve for y.
( )+ − =
22
5 25x x
+ − + =2 2
10 25 25x x x
− =2
2 10 0x x
( )− =2 5 0x x
= 0,5x

12. Solving by Substitution
⚫ Example: Solve by substitution and write the solution as
a set of ordered pairs.
= −
= −
0 5
5
y = −
=
5 5
0
y
( ) ( ) −0, 5 , 5,0
+ =2 2
25x y
− = −5y x

13. Solving by Graphing
⚫ Example: Solve the system by graphing and write your
solution as a set of ordered pairs.
Open desmos.com/calculator (or use the app). Type the
two equations in. On the graph, click on the intersection
point(s). The program should display the coordinates.
Write that as your solution.
− =
+ = −
2
4
2
x y
x y

14. Solving by Graphing
⚫ Example: Solve the system by graphing and write your
solution as a set of ordered pairs.
− =
+ = −
2
4
2
x y
x y
The solution is
( ) ( ) 2,0 , 1, 3− −

15. Absolute Value Equations
⚫ Solve
( )
 + = −

+ + =
2 2
2
3 25
x y
x y

16. Absolute Value Equations
⚫ Solve
( )
 + = −

+ + =
2 2
2
3 25
x y
x y
= − −2y x
( )= − −
22
2y x
( ) ( )+ + − − =
2 2
3 2 25x x
+ + + + + =2 2
6 9 4 4 25x x x x
+ + − =2
2 10 13 25 0x x
+ − =2
2 10 12 0x x
( )( )+ − =2 6 1 0x x
= −6,1x
You can eliminate the
absolute value by squaring
both sides.

17. Absolute Value Equations
⚫ Solve
( )
 + = −

+ + =
2 2
2
3 25
x y
x y
= − −2y x = −6,1x
( )= − − −6 2y = − −1 2y
= −
=
6 2
4
= −3
not possible

= 4y( ) ( ) − − −6,4 , 6, 4

18. Absolute Value Equations
⚫ The graph of this system
shows the solutions:

19. Final Note
⚫ Although I have shown you how to find solutions by
graphing, I expect you to be able to solve by any method.
Some of the questions I ask on the classwork checks,
quizzes, and tests will be structured so that you will
need to know the other methods as well. This is
especially important if your answer is an irrational
number (such as , for example) – Desmos will only
give you a decimal approximation.
5 2

20. Classwork
⚫ College Algebra & Trigonometry
⚫ Page 894: 12-32 (4), page 876: 36-46 (even),
page 850: 48-52 (even)
⚫ 9.5 Classwork Check
⚫ Quiz 9.3