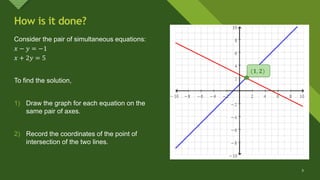
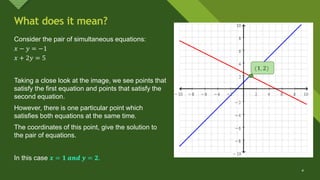
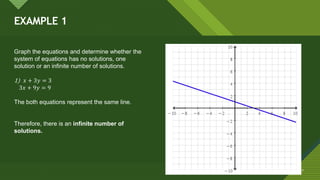
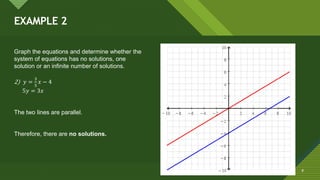
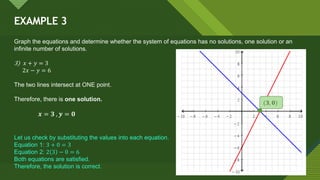
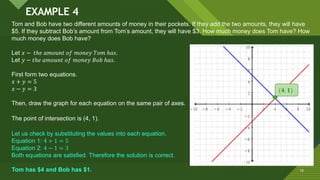
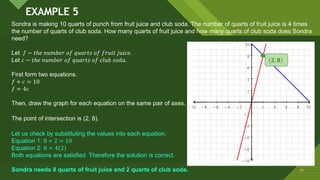
This document discusses solving systems of simultaneous linear equations graphically. It explains that the solution is found by graphing both equations on the same coordinate plane and finding the point where the lines intersect. This intersection point provides the solution values for the variables. Examples are provided to illustrate that the system can have one solution, no solution, or infinite solutions depending on whether the graphs intersect at one point, are parallel, or coincide. Steps for the graphical method are outlined.

1. Click to edit Master title style
1
Simultaneous
Linear Equations
Graphical Solution

2. Click to edit Master title style
2 2
INTRODUCTION

3. Click to edit Master title style
3
How is it done?
Consider the pair of simultaneous equations:
𝑥 − 𝑦 = −1
𝑥 + 2𝑦 = 5
To find the solution,
1) Draw the graph for each equation on the
same pair of axes.
2) Record the coordinates of the point of
intersection of the two lines.
3
(𝟏, 𝟐)

4. Click to edit Master title style
4
What does it mean?
Consider the pair of simultaneous equations:
𝑥 − 𝑦 = −1
𝑥 + 2𝑦 = 5
Taking a close look at the image, we see points that
satisfy the first equation and points that satisfy the
second equation.
However, there is one particular point which
satisfies both equations at the same time.
The coordinates of this point, give the solution to
the pair of equations.
In this case 𝒙 = 𝟏 𝒂𝒏𝒅 𝒚 = 𝟐.
4
(𝟏, 𝟐)

5. Click to edit Master title style
5
Types of Solutions
5
We get different solutions based on how
the graphs look when they are drawn.
• If the graphs intersect at ONE point, then there is one solution.
• If the graphs are parallel and do not intersect, then there are no solutions.
• If the graphs coincide (form the same line), then there is an infinite number of
solutions.

6. Click to edit Master title style
6 6
EXAMPLES

7. Click to edit Master title style
7
EXAMPLE 1
7
Graph the equations and determine whether the
system of equations has no solutions, one
solution or an infinite number of solutions.
1) 𝑥 + 3𝑦 = 3
3𝑥 + 9𝑦 = 9
The both equations represent the same line.
Therefore, there is an infinite number of
solutions.

8. Click to edit Master title style
8
EXAMPLE 2
8
Graph the equations and determine whether the
system of equations has no solutions, one
solution or an infinite number of solutions.
2) 𝑦 =
3
5
𝑥 − 4
5𝑦 = 3𝑥
The two lines are parallel.
Therefore, there are no solutions.

9. Click to edit Master title style
9
EXAMPLE 3
9
Graph the equations and determine whether the system of equations has no solutions, one solution or an
infinite number of solutions.
3) 𝑥 + 𝑦 = 3
2𝑥 − 𝑦 = 6
The two lines intersect at ONE point.
Therefore, there is one solution.
𝒙 = 𝟑 , 𝒚 = 𝟎
Let us check by substituting the values into each equation.
Equation 1: 3 + 0 = 3
Equation 2: 2 3 − 0 = 6
Both equations are satisfied.
Therefore, the solution is correct.
(𝟑, 𝟎)

10. Click to edit Master title style
10
EXAMPLE 4
10
Tom and Bob have two different amounts of money in their pockets. If they add the two amounts, they will have
$5. If they subtract Bob’s amount from Tom’s amount, they will have $3. How much money does Tom have? How
much money does Bob have?
Let 𝑥 − 𝑡ℎ𝑒 𝑎𝑚𝑜𝑢𝑛𝑡 𝑜𝑓 𝑚𝑜𝑛𝑒𝑦 𝑇𝑜𝑚 ℎ𝑎𝑠.
Let 𝑦 − 𝑡ℎ𝑒 𝑎𝑚𝑜𝑢𝑛𝑡 𝑜𝑓 𝑚𝑜𝑛𝑒𝑦 𝐵𝑜𝑏 ℎ𝑎𝑠.
First form two equations.
𝑥 + 𝑦 = 5
𝑥 − 𝑦 = 3
Then, draw the graph for each equation on the same pair of axes.
The point of intersection is (4, 1).
Let us check by substituting the values into each equation.
Equation 1: 4 + 1 = 5
Equation 2: 4 − 1 = 3
Both equations are satisfied. Therefore the solution is correct.
Tom has $4 and Bob has $1.
(𝟒, 𝟏)

11. Click to edit Master title style
11
EXAMPLE 5
11
Sondra is making 10 quarts of punch from fruit juice and club soda. The number of quarts of fruit juice is 4 times
the number of quarts of club soda. How many quarts of fruit juice and how many quarts of club soda does Sondra
need?
Let 𝑓 − 𝑡ℎ𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑞𝑢𝑎𝑟𝑡𝑠 𝑜𝑓 𝑓𝑟𝑢𝑖𝑡 𝑗𝑢𝑖𝑐𝑒.
Let 𝑐 − 𝑡ℎ𝑒 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑞𝑢𝑎𝑟𝑡𝑠 𝑜𝑓 𝑐𝑙𝑢𝑏 𝑠𝑜𝑑𝑎.
First form two equations.
𝑓 + 𝑐 = 10
𝑓 = 4𝑐
Then, draw the graph for each equation on the same pair of axes.
The point of intersection is (2, 8).
Let us check by substituting the values into each equation.
Equation 1: 8 + 2 = 10
Equation 2: 8 = 4(2)
Both equations are satisfied. Therefore the solution is correct.
Sondra needs 8 quarts of fruit juice and 2 quarts of club soda.
(𝟐, 𝟖)

12. Click to edit Master title style
12
STEPS TO SOLVE SIMULTANEOUS EQUATIONS GRAPHICALLY
12
1. Ensure both equations are in slope-intercept form.
𝑦 = 𝑚𝑥 + 𝑐
2. Graph both equations on the same pair of axes.
3. Record the coordinates of the intersection point of the two graphs. This is the
solution.
4. Check the solution to make sure it is correct.

13. Click to edit Master title style
13
The End.