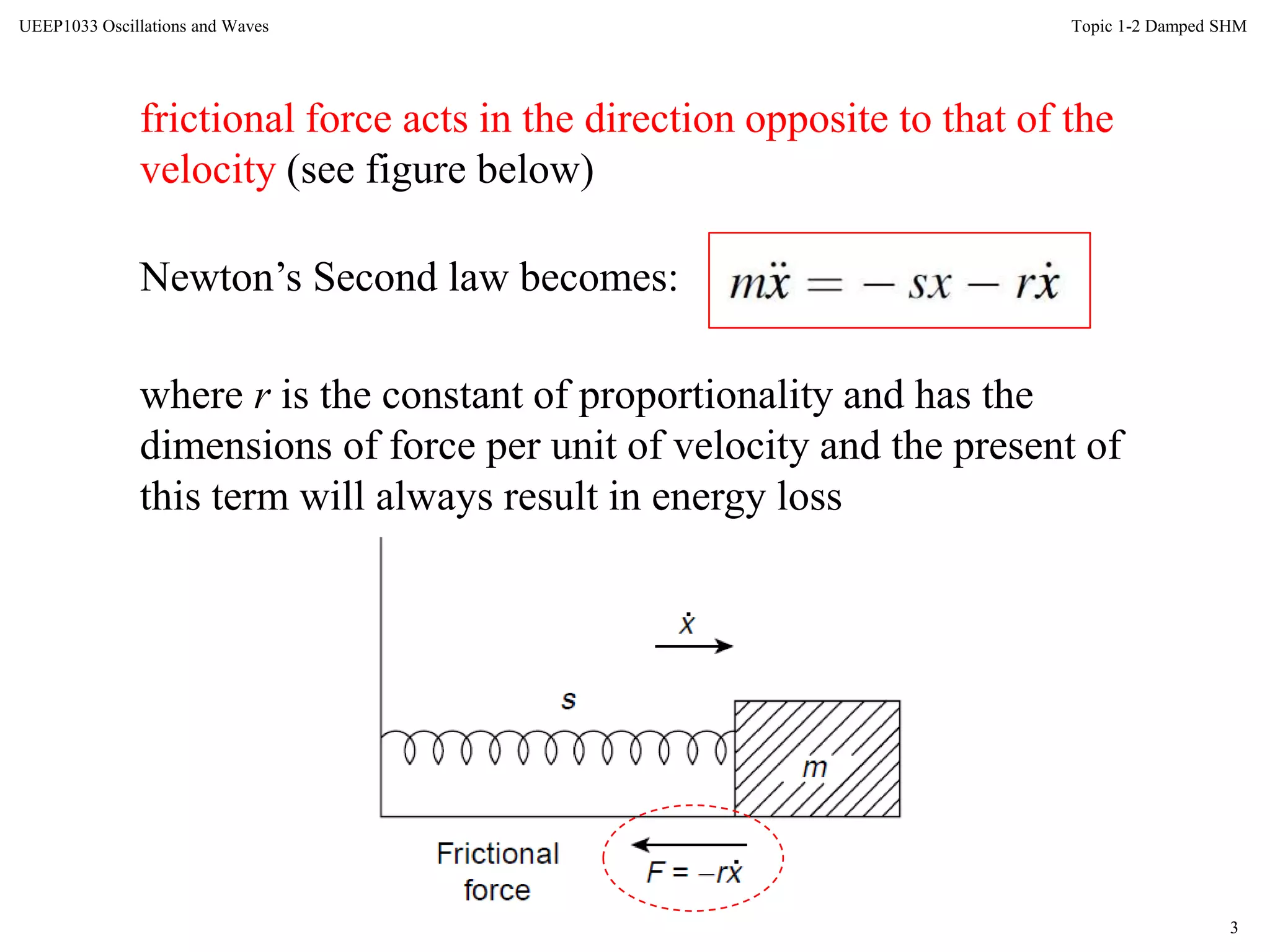
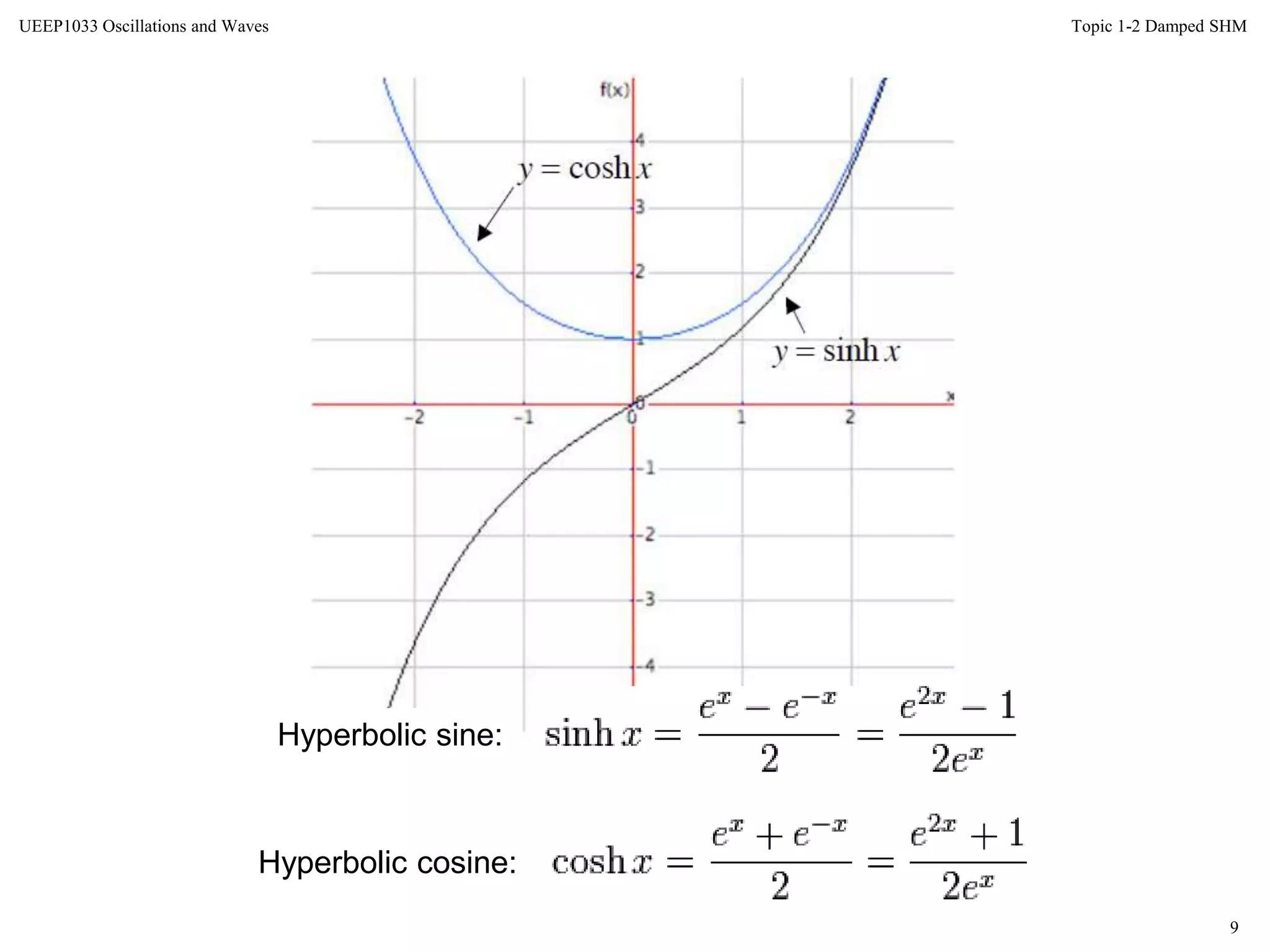
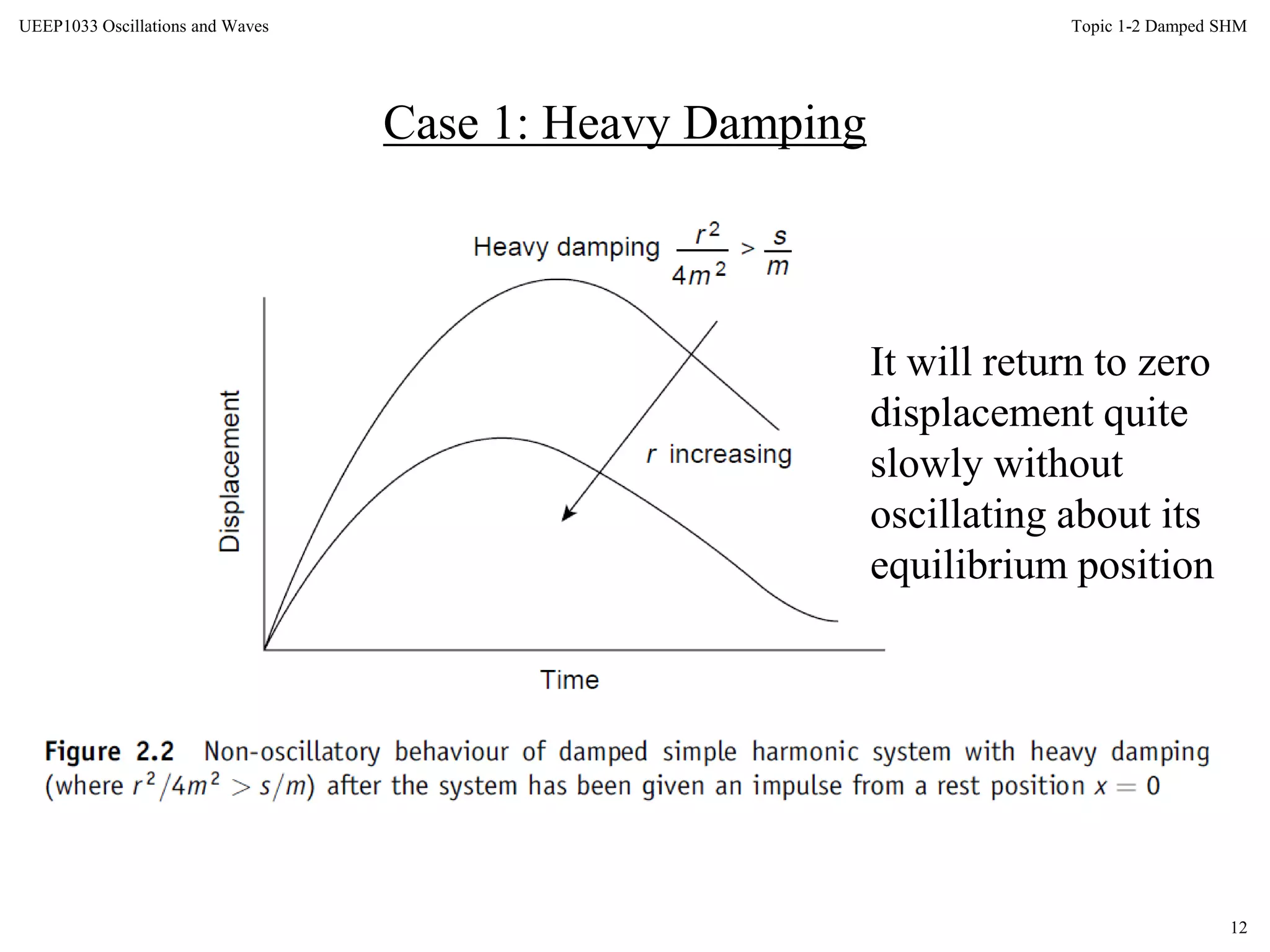
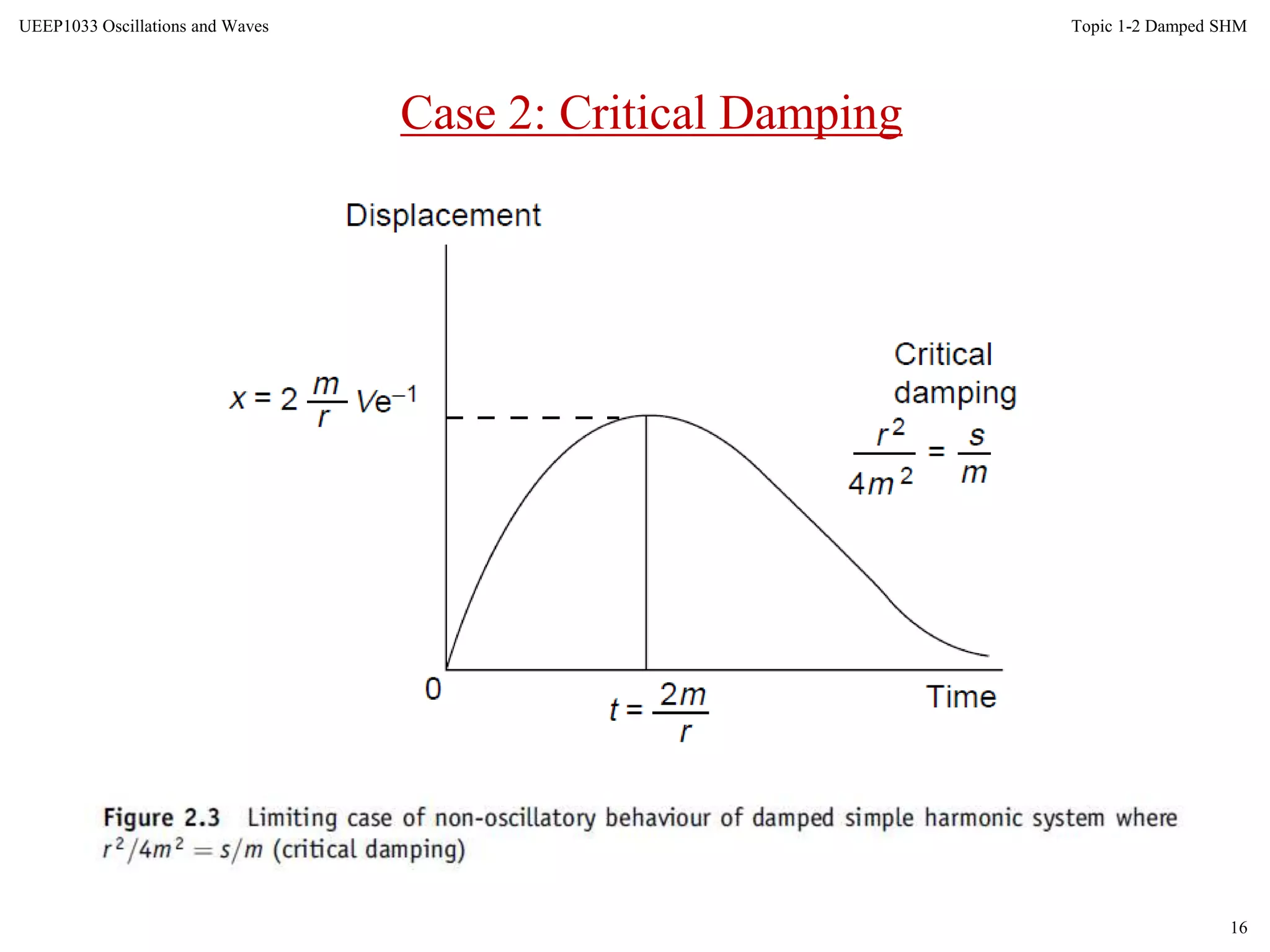
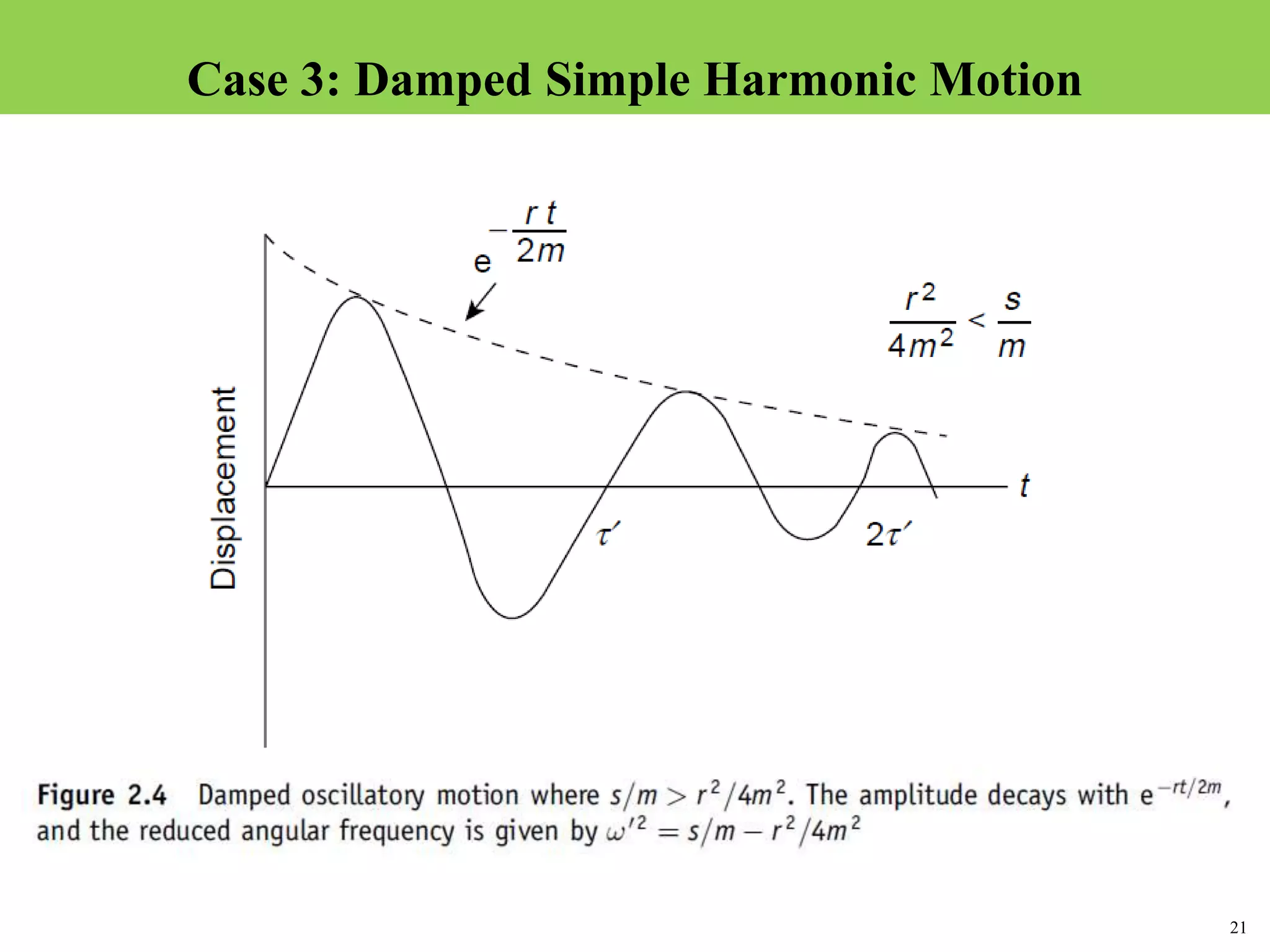
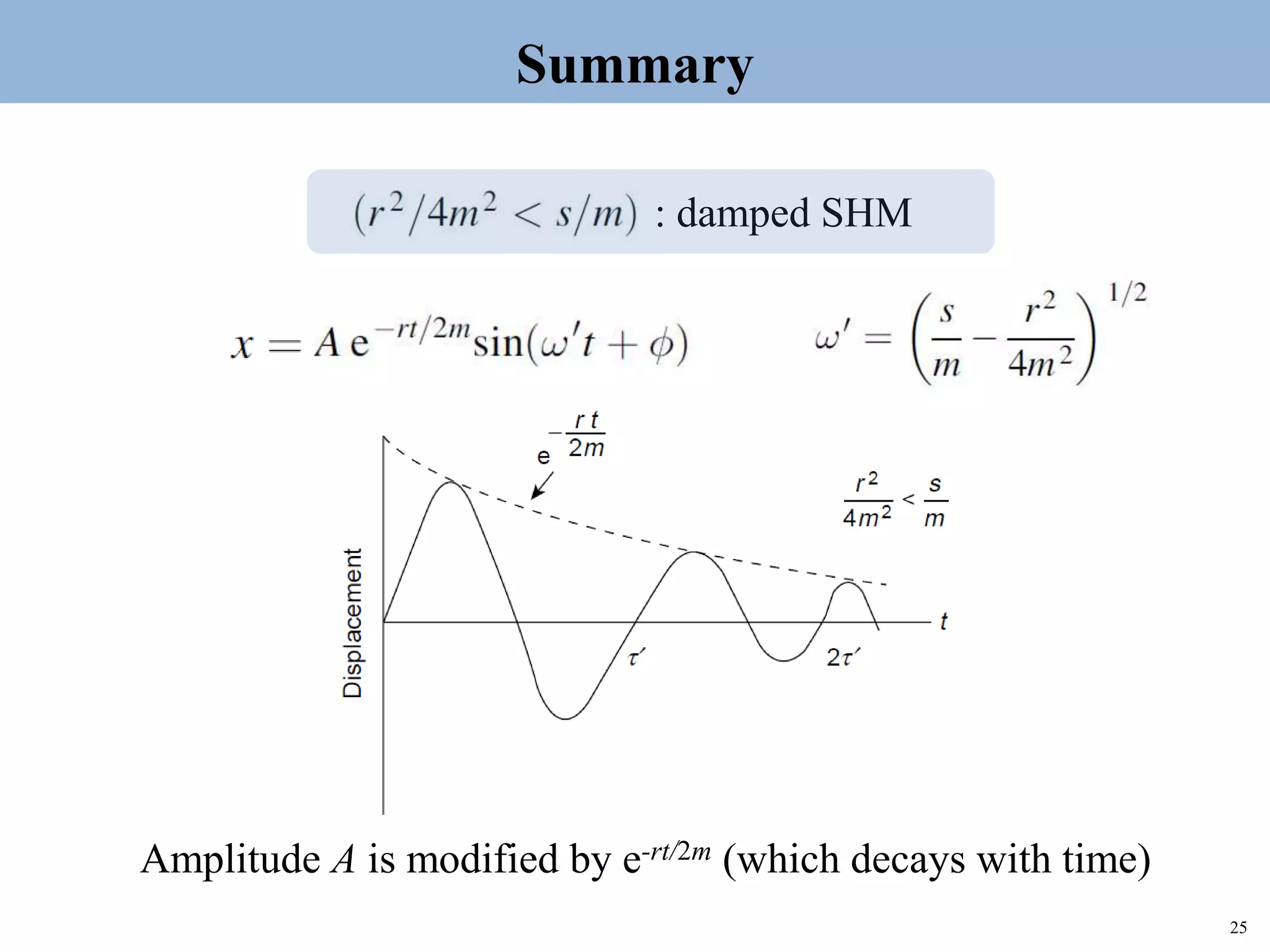
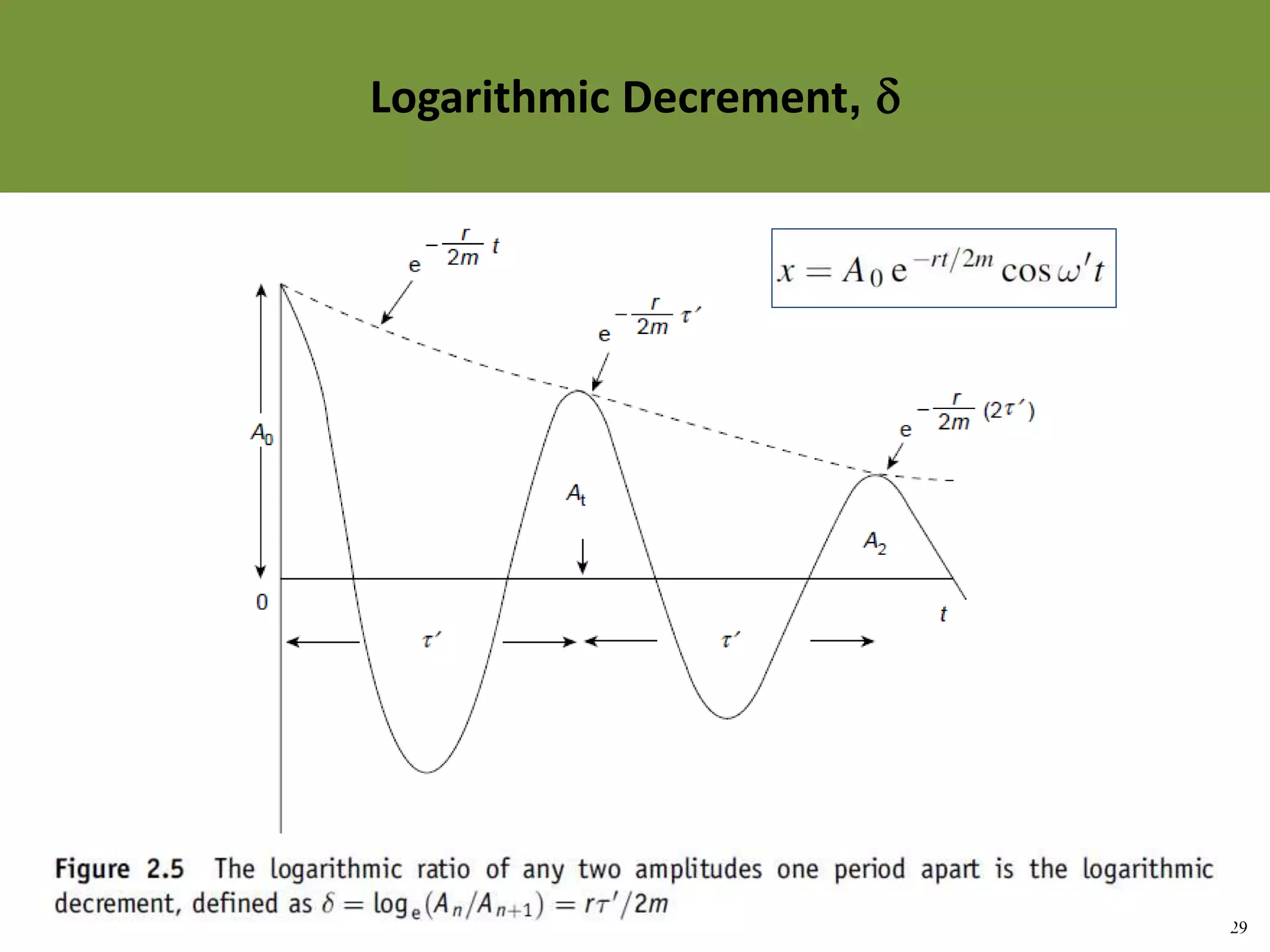
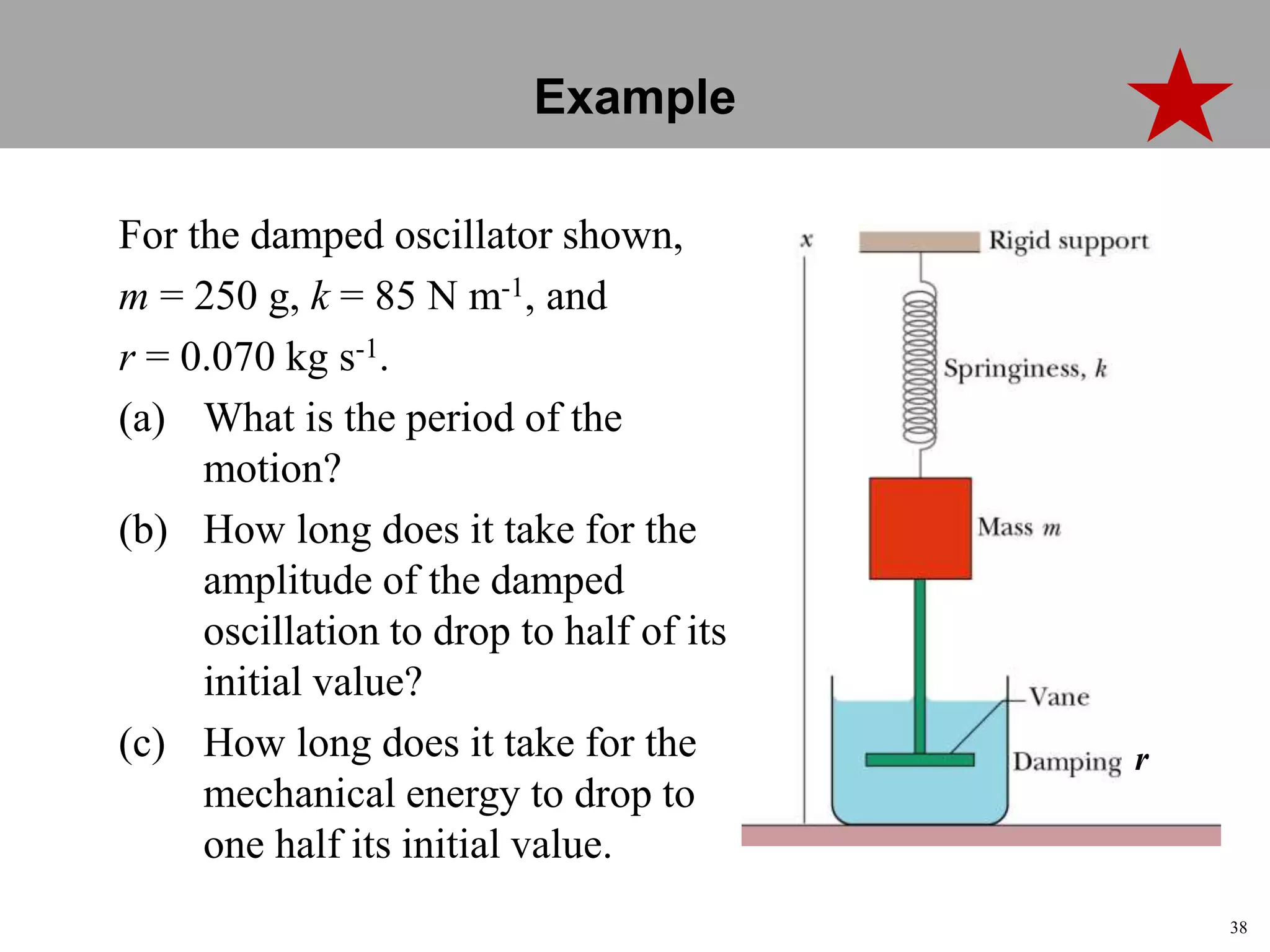
The document discusses damped oscillations, where some energy is lost through a resistive process. There are three cases of damped oscillations: heavy damping results in non-oscillatory behavior and returns to equilibrium slowly; critical damping balances damping and stiffness for the fastest return to equilibrium; light damping results in oscillatory damped simple harmonic motion where the amplitude decays over time. Methods to describe damping include the logarithmic decrement, relaxation time, and quality factor Q.