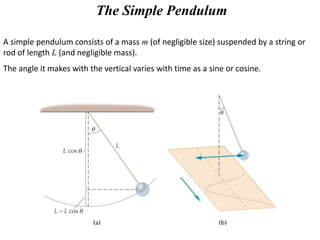
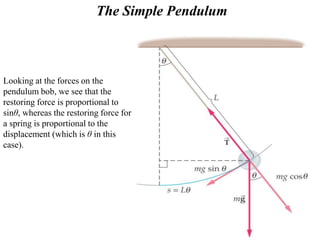
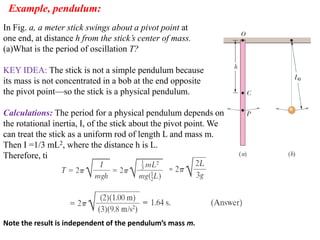
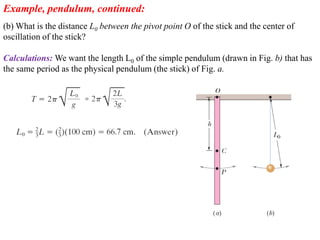
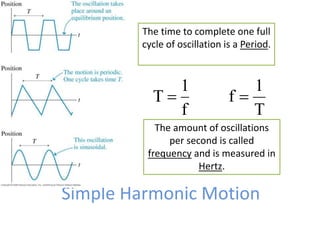
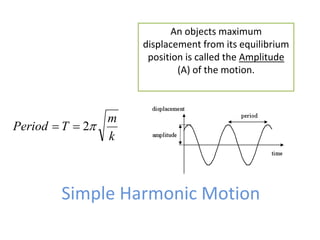
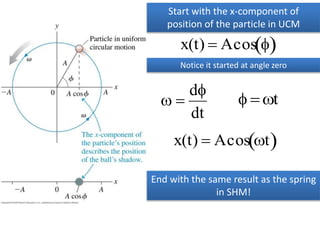
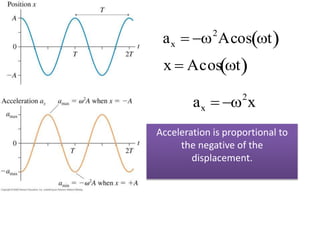
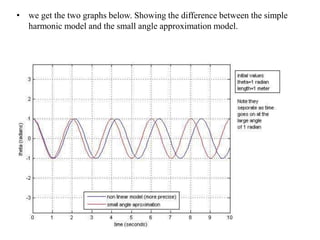
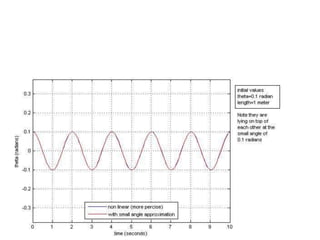
This document discusses the simple pendulum. It describes a simple pendulum as consisting of a mass suspended by a string of negligible mass, with the angle varying sinusoidally with time. The restoring force is proportional to the sine of the angle, allowing it to be treated mathematically similarly to a mass on a spring. The period of a pendulum depends only on its length. Several examples are provided to illustrate physical pendulums and calculating oscillation properties like period. Assumptions of the simple pendulum model are noted.

1. THE SIMPLE PENDULUM (ODE)
• NAKRANI DARSHAN D (D -17)
• PATIL DIPESH J (D-57)
• MODI RAHUL Y ( D- 15)
AEM TOPIC:

2. The Simple Pendulum
A simple pendulum consists of a mass m (of negligible size) suspended by a string or
rod of length L (and negligible mass).
The angle it makes with the vertical varies with time as a sine or cosine.

3. The Simple Pendulum
Looking at the forces on the
pendulum bob, we see that the
restoring force is proportional to
sinθ, whereas the restoring force for
a spring is proportional to the
displacement (which is θ in this
case).

4. The Simple Pendulum
Substituting θ for sin θ allows us to treat the pendulum in a mathematically identical
way to the mass on a spring. Therefore, we find that the period of a pendulum depends
only on the length of the string:

5. The Simple Pendulum
In this case, it can be shown that the period depends on the moment of inertia:
Substituting the moment of inertia of a point mass a distance l from the axis of rotation
gives, as expected,

6. Example, pendulum:
In Fig. a, a meter stick swings about a pivot point at
one end, at distance h from the stick’s center of mass.
(a)What is the period of oscillation T?
KEY IDEA: The stick is not a simple pendulum because
its mass is not concentrated in a bob at the end opposite
the pivot point—so the stick is a physical pendulum.
Calculations: The period for a physical pendulum depends on
the rotational inertia, I, of the stick about the pivot point. We
can treat the stick as a uniform rod of length L and mass m.
Then I =1/3 mL2, where the distance h is L.
Therefore, ti
Note the result is independent of the pendulum’s mass m.

7. Simple Harmonic Motion (SHM).
The simple pendulum.
• Calculate the angular frequency of
the SHM of a simple pendulum.
– A simple pendulum is a
pendulum for which all the
mass is located at a single
point at the end of a massless
string.
– There are two forces acting on
the mass: the tension T and the
gravitational force mg.
– The tension T cancels the
radial component of the
gravitational force.

8. Example, pendulum, continued:
(b) What is the distance L0 between the pivot point O of the stick and the center of
oscillation of the stick?
Calculations: We want the length L0 of the simple pendulum (drawn in Fig. b) that has
the same period as the physical pendulum (the stick) of Fig. a.

9. Simple Harmonic Motion
The time to complete one full
cycle of oscillation is a Period.

T 
1
f

f 
1
T
The amount of oscillations
per second is called
frequency and is measured in
Hertz.

10. Simple Harmonic Motion
An objects maximum
displacement from its equilibrium
position is called the Amplitude
(A) of the motion.
k
m
TPeriod 2

11. 
x(t)  Acos  

 
d
dt

 t

x(t)  Acos t 
Start with the x-component of
position of the particle in UCM
End with the same result as the spring
in SHM!
Notice it started at angle zero

12. Initial conditions:
  t  0
We will not always start our clocks at
one amplitude.
x(t)  Acos t  0 

13. Acceleration is at a maximum when the particle is at maximum and
minimum displacement from x=0.
  
 tA
dt
tAd
dt
tdv
a x
x


cos
sin
)(
2





14. Acceleration is proportional to
the negative of the
displacement.

ax  2
Acos t 

ax  2
x

x  Acos t 

15. As we found with energy
considerations:
ax  2
x
F  max  kx
max  kx
ax 
k
m
x
According to Newton’s 2nd Law:

ax 
d2
x
dt2
Acceleration is not constant:

d2
x
dt2
 
k
m
x
This is the equation of motion
for a mass on a spring. It is of a
general form called differential
equation.

16. Differential Equations:

d2
x
dt2
 
k
m
x
IT WORKS. Sinusoidal oscillation of SHM is a
result of Newton’s laws!
x  Acos t  0 
d2
x
dt2
 2
Acos t 
dx
dt
 Asin t 

2
Acos t 
k
m
Acos t 
2

k
m

17. • we get the two graphs below. Showing the difference between the simple
harmonic model and the small angle approximation model.

19. Assumptions
• All models are full of assumptions. Some of these assumptions are very accurate,
such as the pendulum is unaffected by the day of the week. Some of these
assumptions are less accurate but we are still going to make them, friction does not
effect the system. Here is a list of some of the more notable assumptions of this
model of a pendulum.
• Friction from both air resistance and the system is negligible.
• The pendulum swings in a perfect plane.
• The arm of the pendulum cannot bend or stretch/compress.
• The arm is mass less.
• Gravity is a constant 9.8 meter/second2.
Applications
• Pendulums have many applications and were utilized often before the digital age.
They are used in clocks and metronomes due to the regularity of their period, in
wrecking balls and playground swings, due to their simple way of building up and
keeping energy.

20. Conclusion
• A pendulum is easy to make and with a little bit of math, easy to
understand, one could even use the swaying of their hammock, assuming a
fairly uniform driving force.

21. Reference
• The Simple Pendulum
www.acs.psu.edu/drussell/Demos/
• Pendulum (mathematics) www.wikipedia.org
• Mathematical Swingers: The Simple Pendulum
as a Log Application
www.http://my.execpc.com.
• R.S.KHURMI PUBLICATION (Theory of Machine
CH-4)