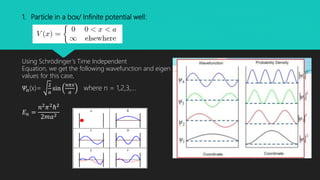
The document discusses Schrödinger's wave equations, both time-dependent and time-independent, detailing their formulations and applications in quantum mechanics. It emphasizes the significance of the time-independent equation in scenarios where potential energy depends solely on position, and illustrates its use in problems like particle in a box and quantum harmonic oscillator. Additionally, it touches on the concept of quantum tunneling and includes multiple-choice questions related to the material.