Report
Share
Download to read offline
Recommended
Recommended
More Related Content
Similar to dampedvibration02-160513044006.pdf
Similar to dampedvibration02-160513044006.pdf (20)
DOMV No 2 RESPONSE OF LINEAR SDOF SYSTEMS TO GENERAL LOADING (2).pdf

DOMV No 2 RESPONSE OF LINEAR SDOF SYSTEMS TO GENERAL LOADING (2).pdf
DOMV No 2 RESPONSE OF LINEAR SDOF SYSTEMS TO GENERAL LOADING (2).pdf

DOMV No 2 RESPONSE OF LINEAR SDOF SYSTEMS TO GENERAL LOADING (2).pdf
Dynamics of Machines and Mechanism, Mechanical Engineering

Dynamics of Machines and Mechanism, Mechanical Engineering
Ae6602 vibrations & elments of aeroelasticity 2 marks

Ae6602 vibrations & elments of aeroelasticity 2 marks
Numerical Study of Strong Free Surface Flow and Wave Breaking

Numerical Study of Strong Free Surface Flow and Wave Breaking
Recently uploaded
Model Call Girl Services in Delhi reach out to us at 🔝 9953056974🔝✔️✔️ Our agency presents a selection of young, charming call girls available for bookings at Oyo Hotels. Experience high-class escort services at pocket-friendly rates, with our female escorts exuding both beauty and a delightful personality, ready to meet your desires. Whether it's Housewives, College girls, Russian girls, Muslim girls, or any other preference, we offer a diverse range of options to cater to your tastes. We provide both in- call and out-call services for your convenience. Our in-call location in Delhi ensures cleanliness, hygiene, and 100% safety, while our out-call services offer doorstep delivery for added ease. We value your time and money, hence we kindly request pic collectors, time-passers, and bargain hunters to refrain from contacting us. Our services feature various packages at competitive rates: One shot: ₹2000/in-call, ₹5000/out-call Two shots with one girl: ₹3500 /in-call, ₱6000/out-call Body to body massage with sex: ₱3000/in-call Full night for one person: ₱7000/in-call, ₱10000/out-call Full night for more than 1 person : Contact us at 🔝 9953056974🔝. for details Operating 24/7, we serve various locations in Delhi, including Green Park, Lajpat Nagar, Saket, and Hauz Khas near metro stations. For premium call girl services in Delhi 🔝 9953056974🔝. Thank you for considering us Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X7![Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X7](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X7](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X79953056974 Low Rate Call Girls In Saket, Delhi NCR
From customer value engagements to hands-on production support, our Services span across every stage of our customers digital transformation journey, to help ensure that every customer is successful in their adoption of our solutions.
• Implementation, Upgrade, Migration, and Maintenance Services
• On-Premises and On-Cloud
• COTS Training Services; On-Site and Virtual
• Software Support Services; Legacy and 3DEXPERIENCE
• Value Engagement & Blueprinting
• Specialized Consulting and Support Services
• Customized Training Services
• Automation and Configuration Services
• Technical Resource Augmentation Services
• Project Management
• Know-how Training (mentoring) and Resource AugmentationNavigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...

Navigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...Arindam Chakraborty, Ph.D., P.E. (CA, TX)
Recently uploaded (20)
Unit 4_Part 1 CSE2001 Exception Handling and Function Template and Class Temp...

Unit 4_Part 1 CSE2001 Exception Handling and Function Template and Class Temp...
Bhubaneswar🌹Call Girls Bhubaneswar ❤Komal 9777949614 💟 Full Trusted CALL GIRL...

Bhubaneswar🌹Call Girls Bhubaneswar ❤Komal 9777949614 💟 Full Trusted CALL GIRL...
Standard vs Custom Battery Packs - Decoding the Power Play

Standard vs Custom Battery Packs - Decoding the Power Play
Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X7![Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X7](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
![Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X7](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7)
Call Girls in South Ex (delhi) call me [🔝9953056974🔝] escort service 24X7
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX

XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Theory of Time 2024 (Universal Theory for Everything)

Theory of Time 2024 (Universal Theory for Everything)
Navigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...

Navigating Complexity: The Role of Trusted Partners and VIAS3D in Dassault Sy...
Tamil Call Girls Bhayandar WhatsApp +91-9930687706, Best Service

Tamil Call Girls Bhayandar WhatsApp +91-9930687706, Best Service
"Lesotho Leaps Forward: A Chronicle of Transformative Developments"

"Lesotho Leaps Forward: A Chronicle of Transformative Developments"
PE 459 LECTURE 2- natural gas basic concepts and properties

PE 459 LECTURE 2- natural gas basic concepts and properties
dampedvibration02-160513044006.pdf
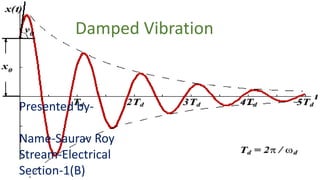
- 1. Damped Vibration Presented by- Name-Saurav Roy Stream-Electrical Section-1(B)
- 4. What is Damped Vibration? • When a body or a particle vibrates it faces a number of frictional forces(Internal or external).This forces decreases the amplitude of vibration of time and the motion of the body ultimately stops altogether.Such vibration of decaying amplitude is called Damped Vibration.
- 5. Differential Equation of Damped Harmonic Vibration The Newton's 2nd Law motion equation is: This is in the form of a homogeneous second order differential equation and has a solution of the form: Substituting this form gives an auxiliary equation for λ. The roots of the quadratic auxiliary equation are
- 6. Damping Coefficient When a damped oscillator is subject to a damping force which is linearly dependent upon the velocity, such as viscous damping, the oscillation will have exponential decay terms which depend upon a damping coefficient. If the damping force is of the form: then the damping coefficient is given by:
- 7. DAMPED FREE VIBRATION SDOF • If viscous damping is assumed, the equation of motion becomes: • There are 3 types of solution to this, defined as: • Critically Damped • Overdamped • Underdamped • A swing door with a dashpot closing mechanism is a good analogy • If the door oscillates through the closed position it is underdamped • If it creeps slowly to the closed position it is overdamped. • If it closes in the minimum possible time, with no overswing, it is critically damped. 0 ) ( ) ( ) ( t ku t u b t u m
- 8. Frequency and period as before Amplitude is a function of damping 2% Damping 5% Damping DAMPED VIBRATION Time Disp.
- 9. DAMPING WITH FORCED VIBRATION Apply a harmonic forcing function: note that is the DRIVING or INPUT frequency The equation of motion becomes The solution consists of two terms: The initial response, due to initial conditions which decays rapidly in the presence of damping The steady-state response as shown: This equation is described on the next page t p sin t p t ku t u b t u m sin ) ( ) ( ) ( 2 2 2 2 ) / 2 ( ) 1 ( ) sin( / ) ( n n t k p t u
- 10. DAMPING WITH FORCED VIBRATION This equation deserves inspection as it shows several important dynamic characteristics: At = n this term = (2 )^2 and controls the scaling of the response From this is derived the Dynamic Magnification Factor 1/2 2 2 2 2 ) / 2 ( ) 1 ( ) sin( / ) ( n n t k p t u This is the static loading and dominates as tends to 0.0 At = n this term = 0.0 With no damping present this results in an infinite response Phase lead of the response relative to the input (see next page) At >> n both terms drive the response to 0.0
- 11. Summary: For Magnification factor 1 (static solution) Phase angle 360º (response is in phase with the force) For Magnification factor 0 (no response) Phase angle 180º (response has opposite sign of force) For Magnification factor 1/2 Phase angle 270º 1 ω ω n 1 ω ω n 1 ω ω n DAMPING WITH FORCED VIBRATION (Cont.)
- 12. THANK YOU