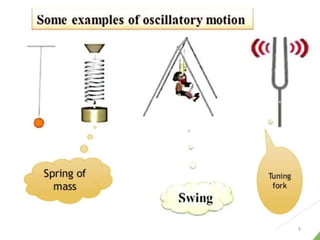
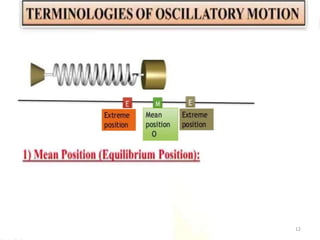
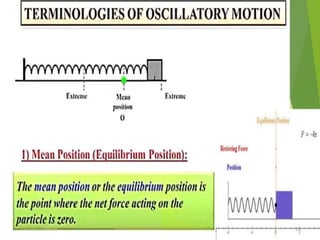
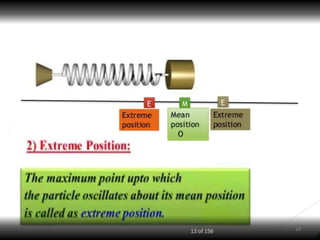
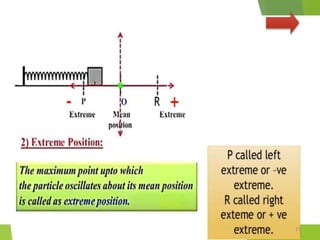
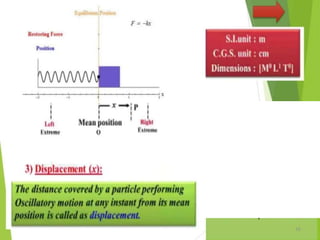
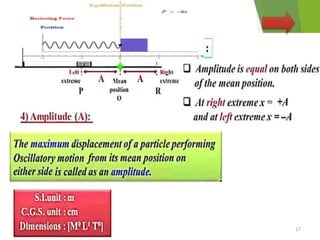
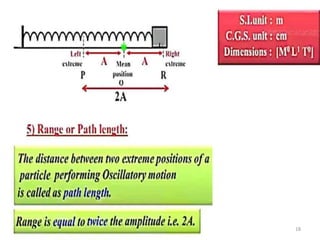
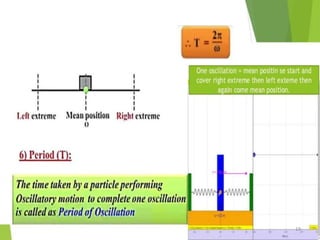
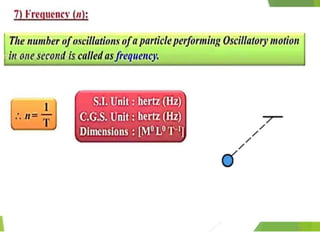
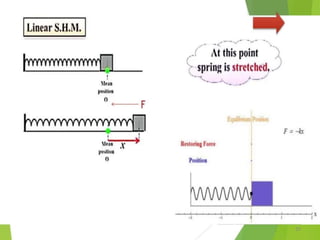
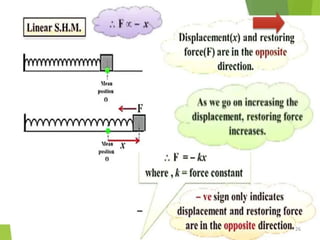
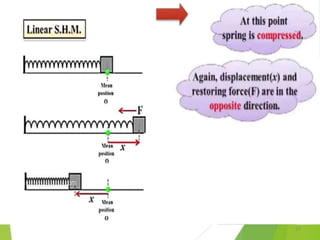
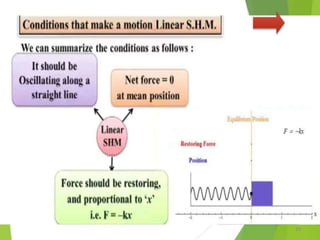
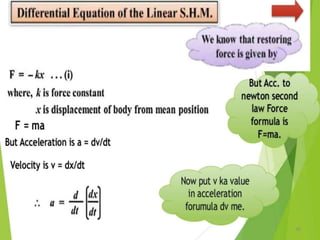
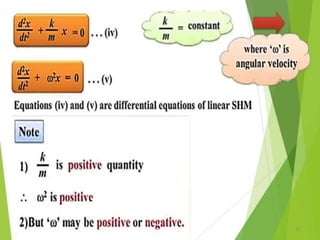
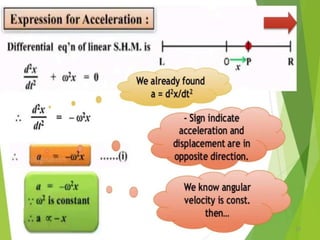
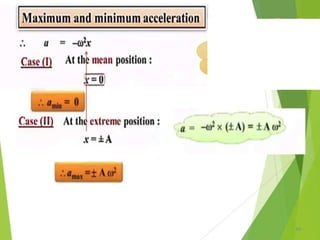
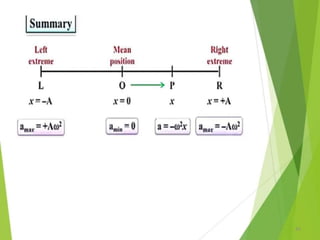
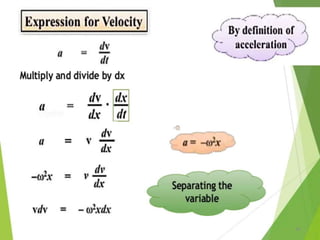
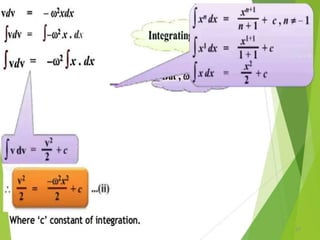
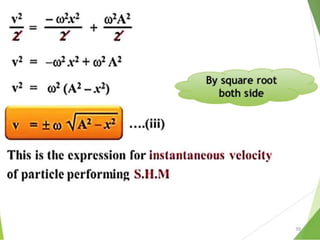
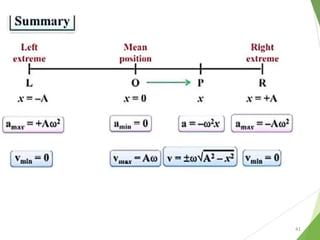
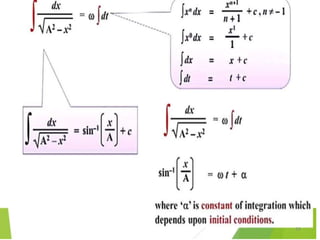
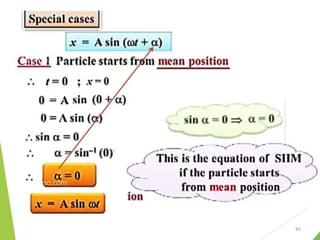
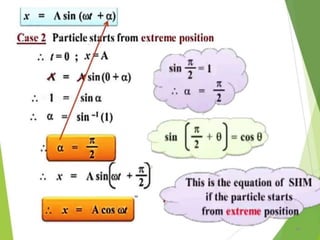
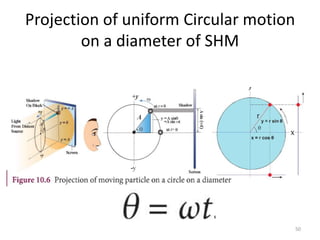
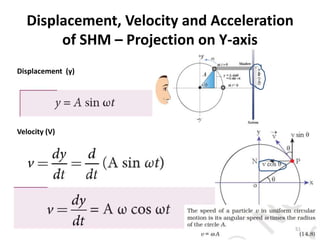
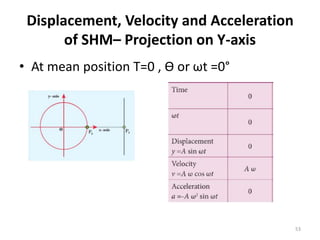
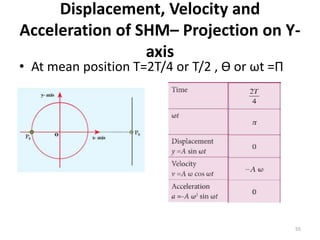
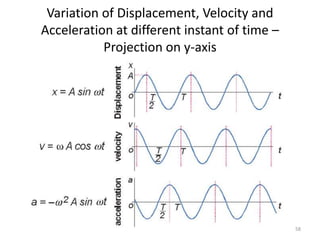
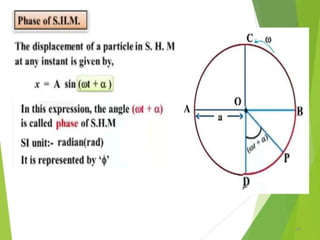
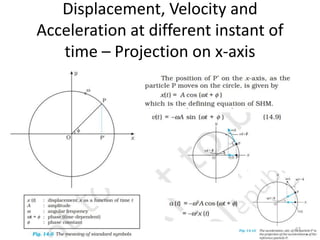
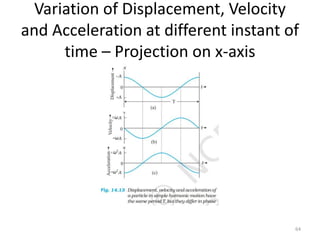
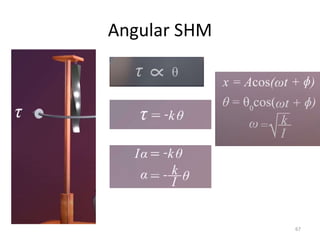
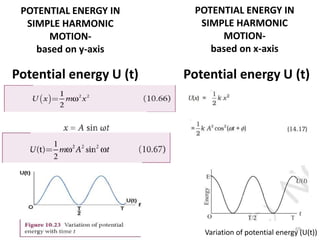
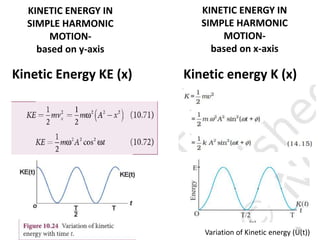
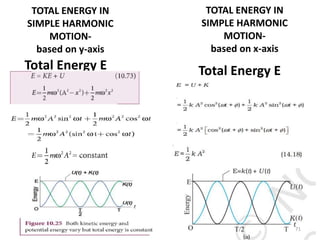
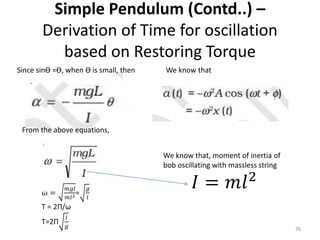
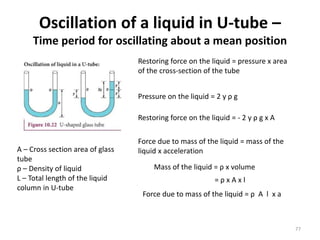
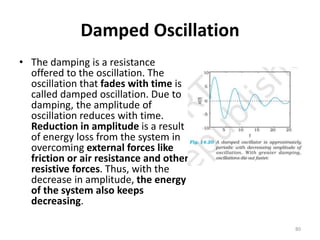
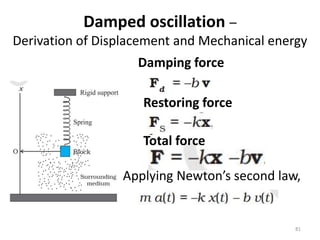
This document discusses oscillations, including different types of motion like simple harmonic motion. It covers topics such as periodic motion, terminologies, linear and angular simple harmonic motion, energies in SHM, examples of SHM like a spring and pendulum, and equations of motion. It also discusses free oscillations, damped oscillations, and forced oscillations, specifically resonance. Forces, displacements, velocities, and accelerations of SHM are examined. Combinations of springs and their effective spring constants are analyzed.

1. OSCILLATIONS

2. Overview
- Types of motion
- Periodic motion
- Terminologies in Oscillations
- Simple Harmonic Motion - Linear SHM – Oscillations due to a spring
- Combination of springs
- Angular SHM
- Energies in SHM- Kinetic, Potential
- Examples of SHM – Oscillations due to spring, Simple pendulum,
Oscillation of liquid in a U-tube
- Free Oscillation
- Damped Oscillation
- Forced Oscillation – Resonance
2

3. TYPES OF MOTION
3

4. 4

5. 5

6. 6

7. 7

8. 8

9. 9

10. 10

11. 11

12. 12

13. 13

14. 14

15. 15

16. 16

17. 17

18. 18

19. 19

20. 20

21. Equations of Periodic motion
21

22. SIMPLE HARMONIC MOTION
22

23. 23

24. 24

25. 25

26. 26

27. 27

28. 28

29. 29

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. 36

37. 37

38. 38

39. 39

40. 40

41. 41

42. 42

43. 43

44. 44

45. 45

46. 46

47. Combination of springs –
Calculation of Effective spring constant (Ks or Kp)
47
• Springs connected in series
• Total displacement

48. Combination of springs –
Calculation of Effective spring constant (Ks or Kp)
48
• Springs connected in Parallel

49. 49

50. Projection of uniform Circular motion
on a diameter of SHM
50

51. Displacement, Velocity and Acceleration
of SHM – Projection on Y-axis
Displacement (y)
Velocity (V)
51

52. Displacement, Velocity and Acceleration
of SHM– Projection on Y-axis
Velocity (V)
Accleration (a)
52

53. Displacement, Velocity and Acceleration
of SHM– Projection on Y-axis
• At mean position T=0 , Ɵ or ωt =0°
53

54. Displacement, Velocity and
Acceleration of SHM– Projection on Y-
axis
• At mean position T=T/4 , Ɵ or ωt =Π/2
54

55. Displacement, Velocity and
Acceleration of SHM– Projection on Y-
axis
• At mean position T=2T/4 or T/2 , Ɵ or ωt =Π
55

56. Displacement, Velocity and
Acceleration of SHM– Projection on Y-
axis
• At mean position T=3T/4, Ɵ or ωt = 3Π/2
56

57. Displacement, Velocity and
Acceleration of SHM– Projection on Y-
axis
• At mean position T=4T/4 or T , Ɵ or ωt =2Π
57

58. Variation of Displacement, Velocity and
Acceleration at different instant of time –
Projection on y-axis
58

59. 59

60. 60

61. 61

62. 62

63. Displacement, Velocity and
Acceleration at different instant of
time – Projection on x-axis
63

64. Variation of Displacement, Velocity
and Acceleration at different instant of
time – Projection on x-axis
64

65. Other examples of Linear SHM
“Simple harmonic Motion occurs when a particle or object moves back and forth
within a stable equilibrium position under the influence of a restoring force
proportional to its displacement.”
Spring Mass system Pendulum Swing
Shock absorber of a car Strings of a musical instrument Bungee Jumping
65

66. Angular SHM
66

67. Angular SHM
67

68. Linear versus Angular SHM
Linear
Displacement
Acceleration
Mass Moment of
Inertia
Angular
acceleration
Angular
Displacement
Acceleration
Angular
acceleration
Restoring Force Restoring Torque
Angular frequency Angular frequency 68

69. POTENTIAL ENERGY IN
SIMPLE HARMONIC
MOTION-
based on y-axis
Potential energy U (t)
POTENTIAL ENERGY IN
SIMPLE HARMONIC
MOTION-
based on x-axis
Potential energy U (t)
Variation of potential energy (U(t))
69

70. KINETIC ENERGY IN
SIMPLE HARMONIC
MOTION-
based on y-axis
Kinetic Energy KE (x)
KINETIC ENERGY IN
SIMPLE HARMONIC
MOTION-
based on x-axis
Kinetic energy K (x)
Variation of Kinetic energy (U(t))
70

71. TOTAL ENERGY IN
SIMPLE HARMONIC
MOTION-
based on y-axis
Total Energy E
TOTAL ENERGY IN
SIMPLE HARMONIC
MOTION-
based on x-axis
Total Energy E
71

72. Examples of Linear SHM
• Simple pendulum
Considering the normal component,
along the string
72
m is the mass of the bob
l – length f the string

73. Simple Pendulum (Contd..) –
Derivation of Time for oscillation based on
restoring force
73
Considering the Tangential component which is equal to the restoring force

74. Simple Pendulum (Contd..) –
Derivation of Time for oscillation based on
restoring force
74

75. Simple Pendulum (Contd..) –
Derivation of Time for oscillation
based on restoring torque
75
Considering the tangential component , restoring torque is

76. Simple Pendulum (Contd..) –
Derivation of Time for oscillation
based on Restoring Torque
76
Since sinƟ =Ɵ, when Ɵ is small, then We know that
From the above equations,
We know that, moment of inertia of
bob oscillating with massless string
𝐼 = 𝑚𝑙2
ω =
𝑚𝑔𝑙
𝑚𝑙2=
𝑔
𝑙
T = 2Π/ω
T=2Π
𝑙
𝑔

77. Oscillation of a liquid in U-tube –
Time period for oscillating about a mean position
77
Restoring force on the liquid = pressure x area
of the cross-section of the tube
Pressure on the liquid = 2 y ρ g
A – Cross section area of glass
tube
ρ – Density of liquid
L – Total length of the liquid
column in U-tube
Restoring force on the liquid = - 2 y ρ g x A
Force due to mass of the liquid = mass of the
liquid x acceleration
Mass of the liquid = ρ x volume
= ρ x A x l
Force due to mass of the liquid = ρ A l x a

78. Oscillation of a liquid in U-tube –
Time period for oscillating about a mean position
78
Restoring force on the liquid = Force due to mass of the liquid
-2 y ρ g x A = ρ A L a
-2 y g = L a
a = 2 y g / L
a = (2g/L)*y
We know that,
ω =
2𝑔
𝐿
T = 2Π/ω
T=2Π
𝑙
2𝑔

79. Free oscillations
• The free oscillation possesses constant
amplitude and period without any external force
to set the oscillation.
• Ideally, free oscillation does not undergo
damping. But in all-natural systems damping is
observed unless and until any constant external
force is supplied to overcome damping.
• In such a system, the amplitude, frequency and
energy all remain constant.
79

80. Damped Oscillation
• The damping is a resistance
offered to the oscillation. The
oscillation that fades with time is
called damped oscillation. Due to
damping, the amplitude of
oscillation reduces with time.
Reduction in amplitude is a result
of energy loss from the system in
overcoming external forces like
friction or air resistance and other
resistive forces. Thus, with the
decrease in amplitude, the energy
of the system also keeps
decreasing.
80

81. Damped oscillation –
Derivation of Displacement and Mechanical energy
81
Damping force
Restoring force
Total force
Applying Newton’s second law,

82. Damped oscillation –
Derivation of Displacement and Mechanical energy
82
Expressing the eqn. in the form of PDE’s, we get
Where,

83. Damped oscillation –
Derivation of Displacement and Mechanical energy
83
Mechanical Energy of undamped oscillator E(t) = ½ KA2

84. Forced Oscillations
• When a body oscillates by being influenced by
an external periodic force, it is called forced
oscillation. Here, the amplitude of oscillation,
experiences damping but remains constant
due to the external energy supplied to the
system.
• For example, when you push someone on a
swing, you have to keep periodically pushing
them so that the swing doesn’t reduce.
84

85. Forced Oscillations
85

86. Forced Oscillations
86
Expressing the eqn. in the form of PDE’s, we get

87. Forced Oscillation
87

88. Forced Oscillation
• Small Damping, Driving Frequency far from
Natural Frequency – i.e. b=0
• Driving Frequency Close to Natural frequency
- Resonance
88

89. Forced Oscillation –
Example of simple pendulum
• Pendulum 1 and 4 have
the same length
• When pendulum 4
oscillates, pendulum 1
also oscillates
• This happens because in
this the condition for
resonance is satisfied, i.e.
the natural frequency of
the system coincides with
that of the driving force
89

90. Thank you
90