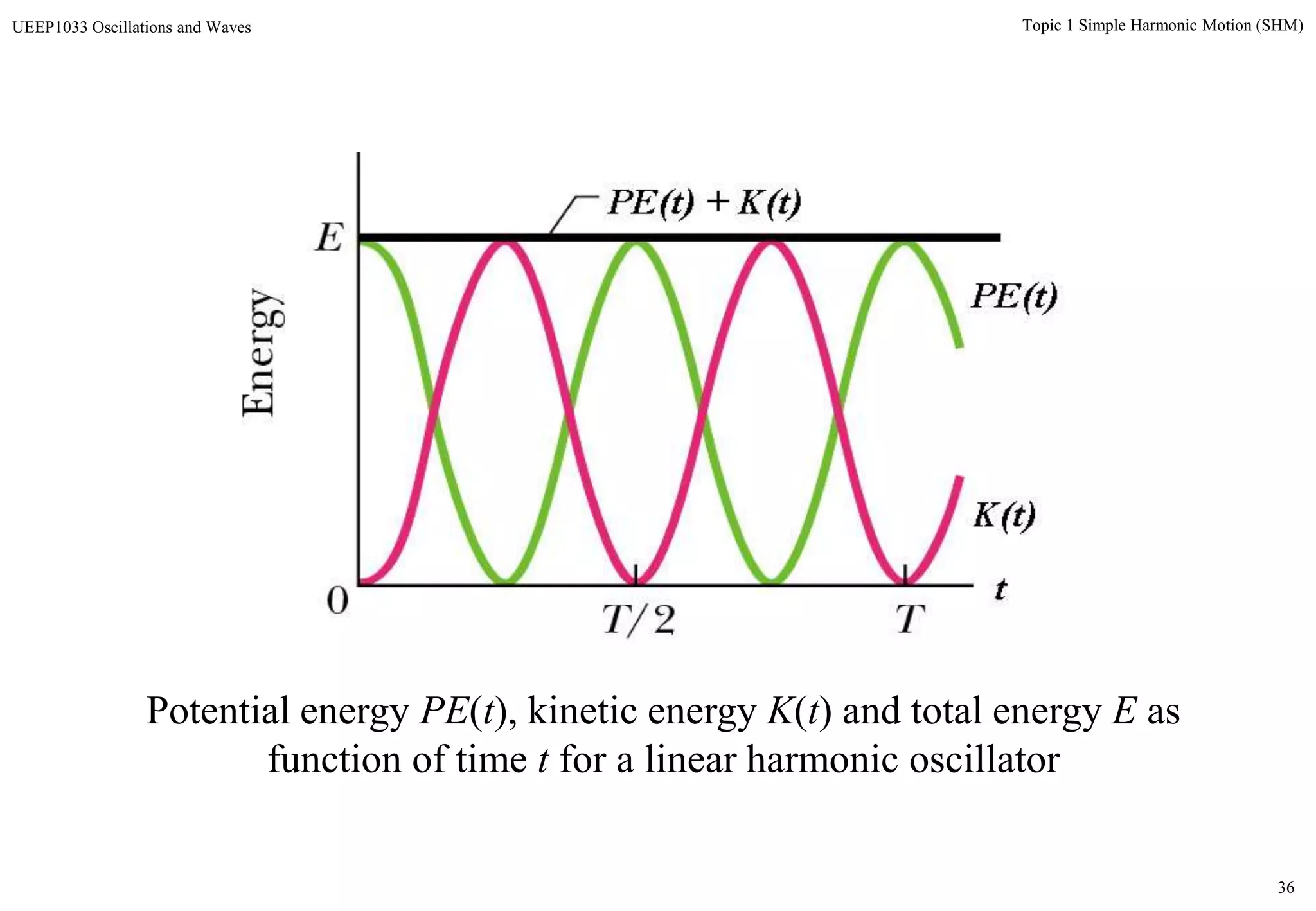
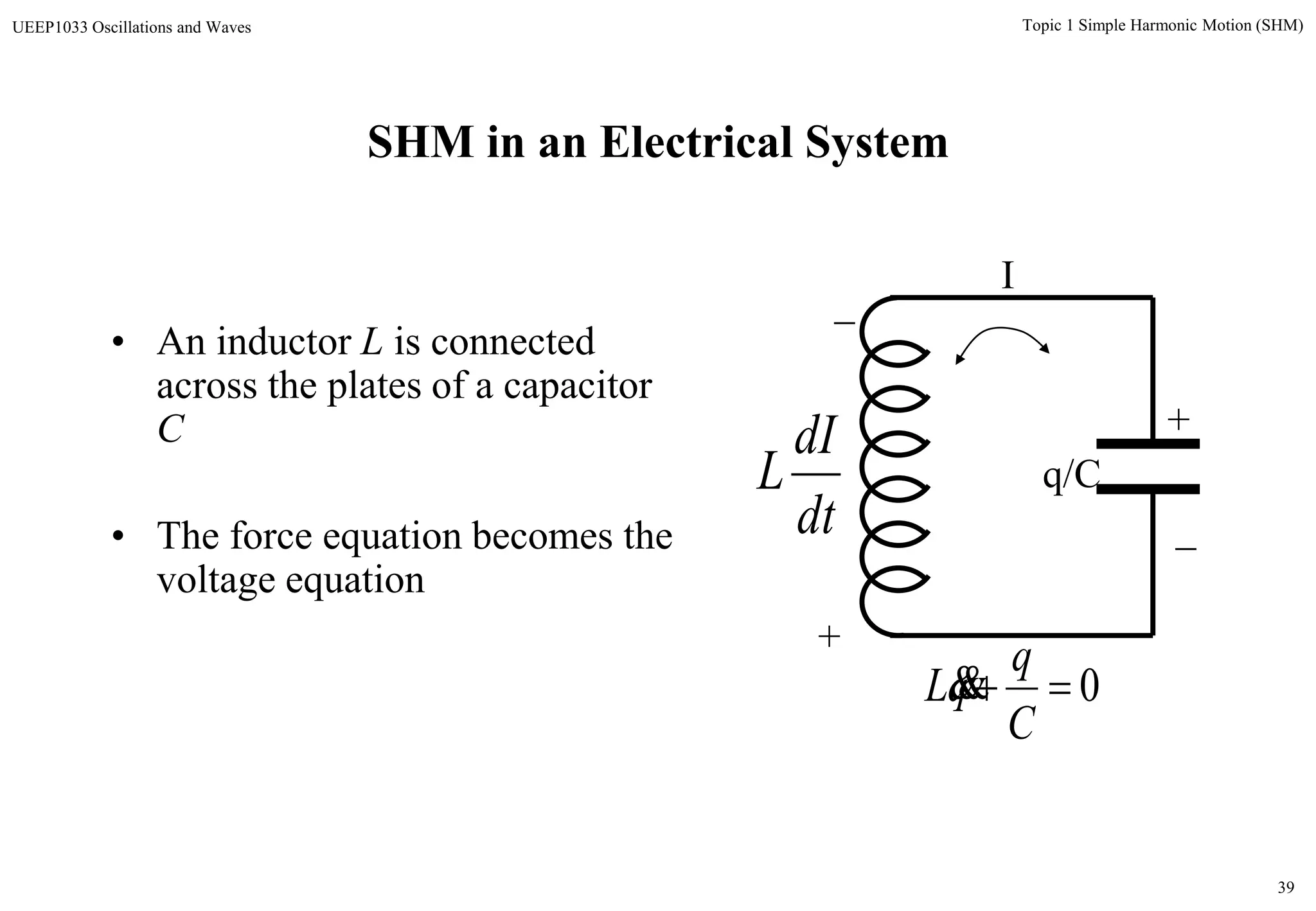
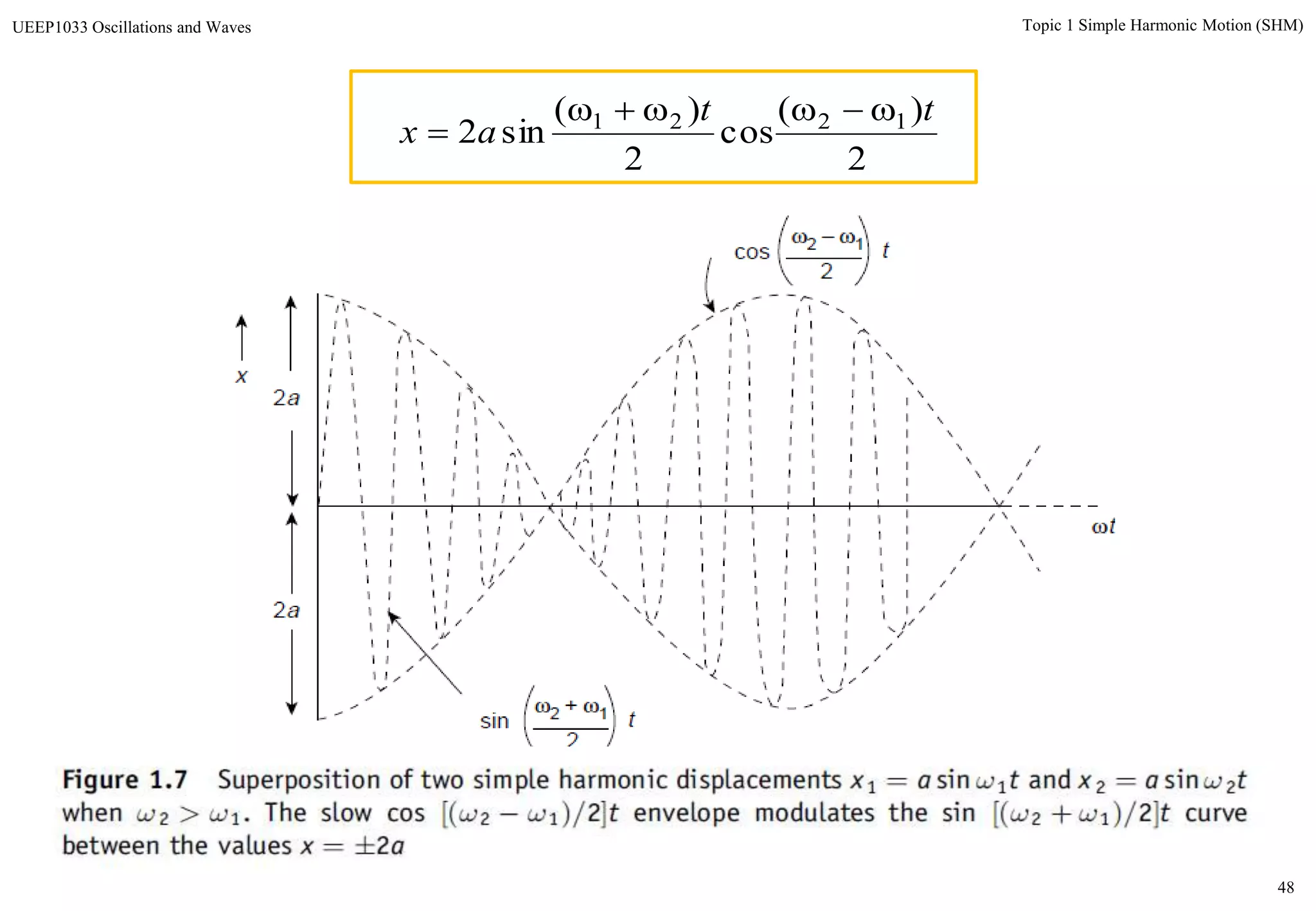
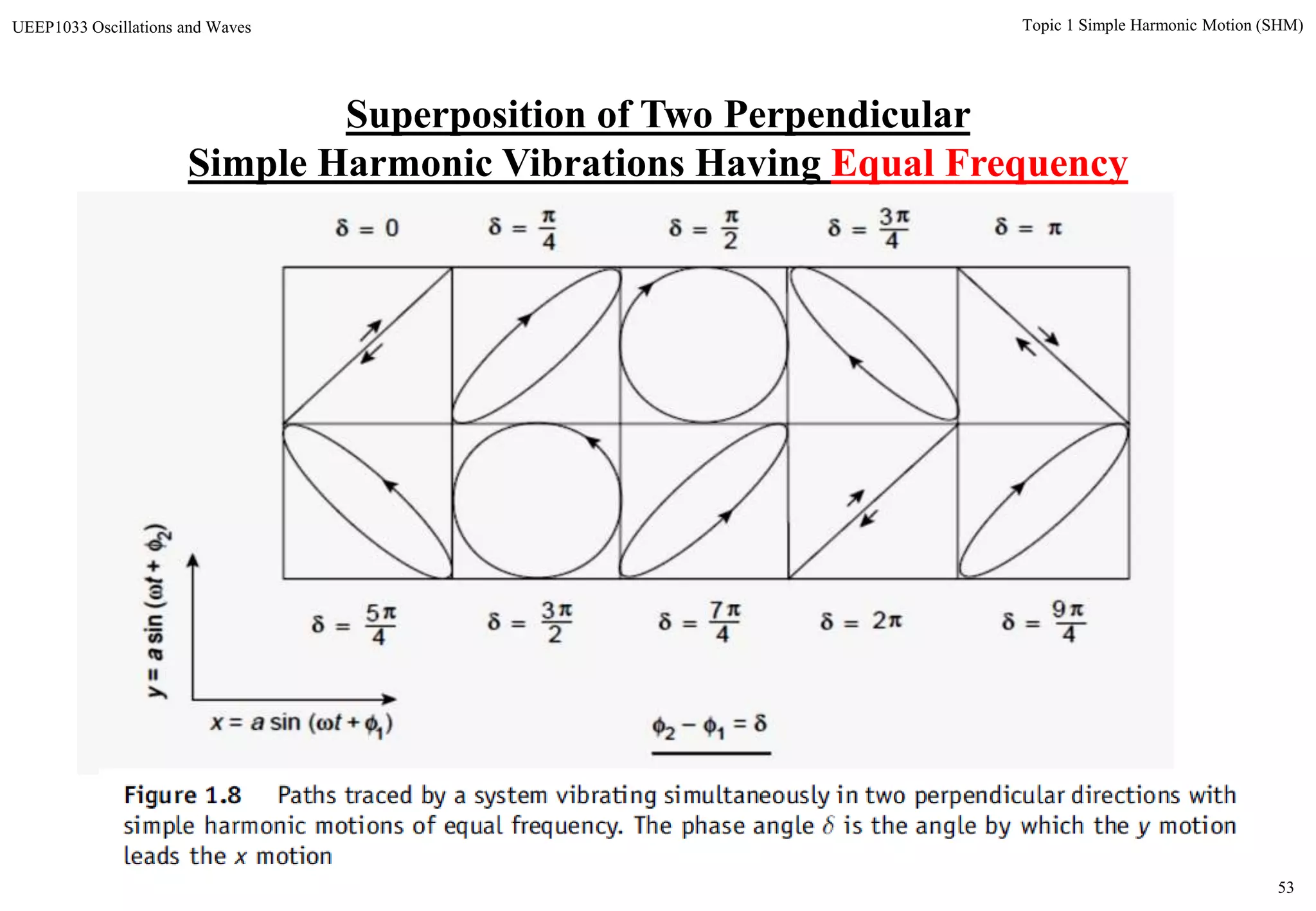
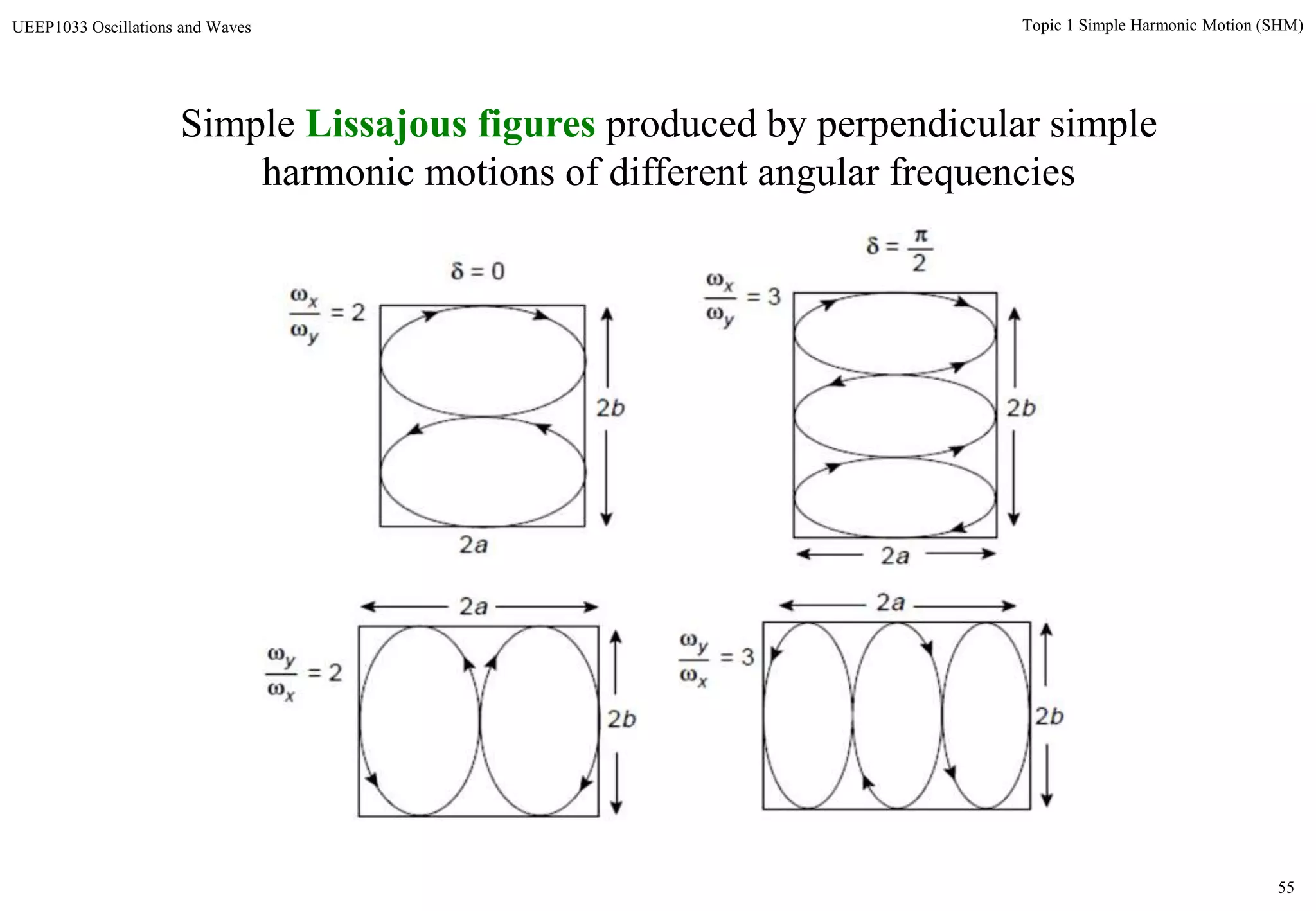
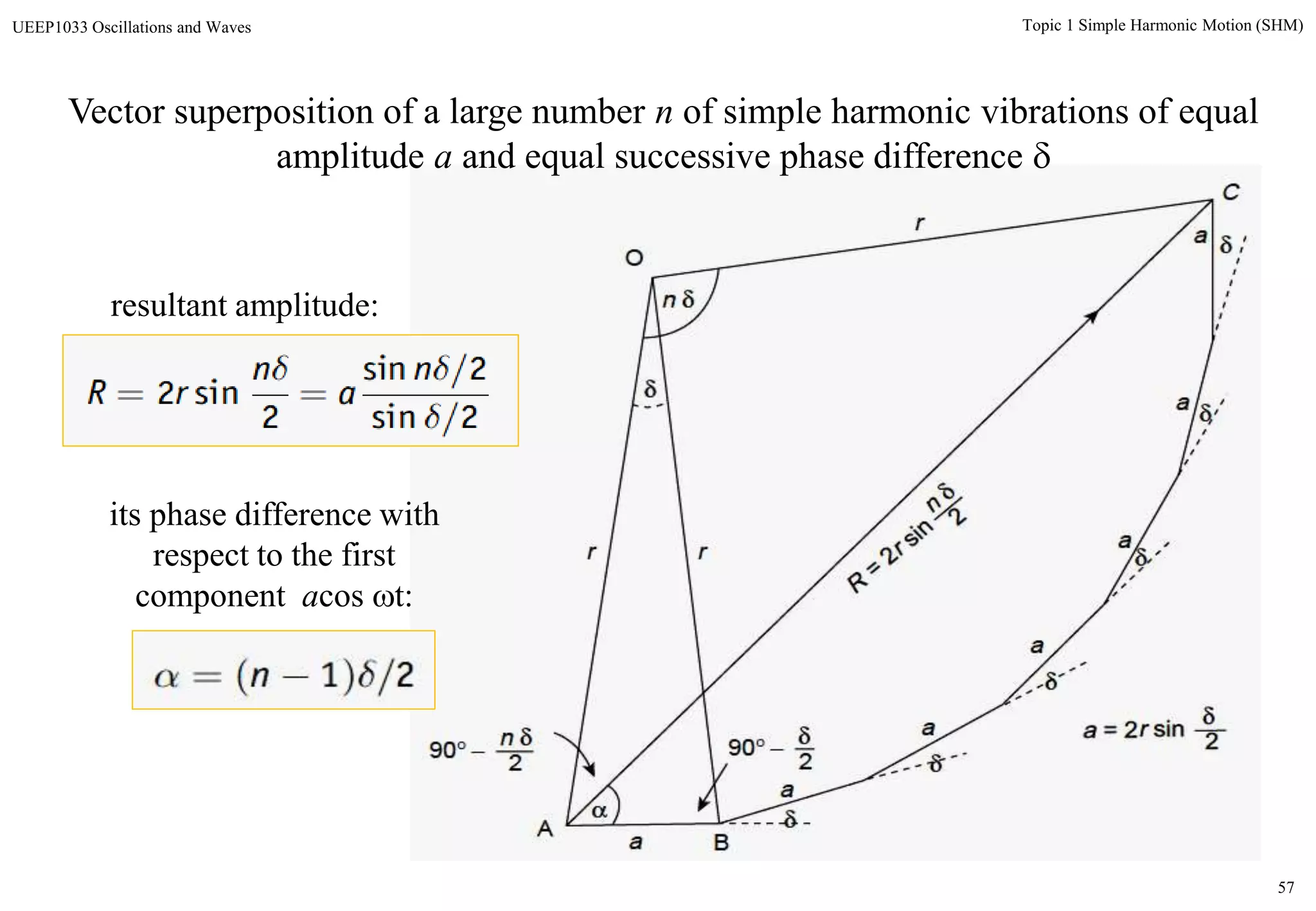
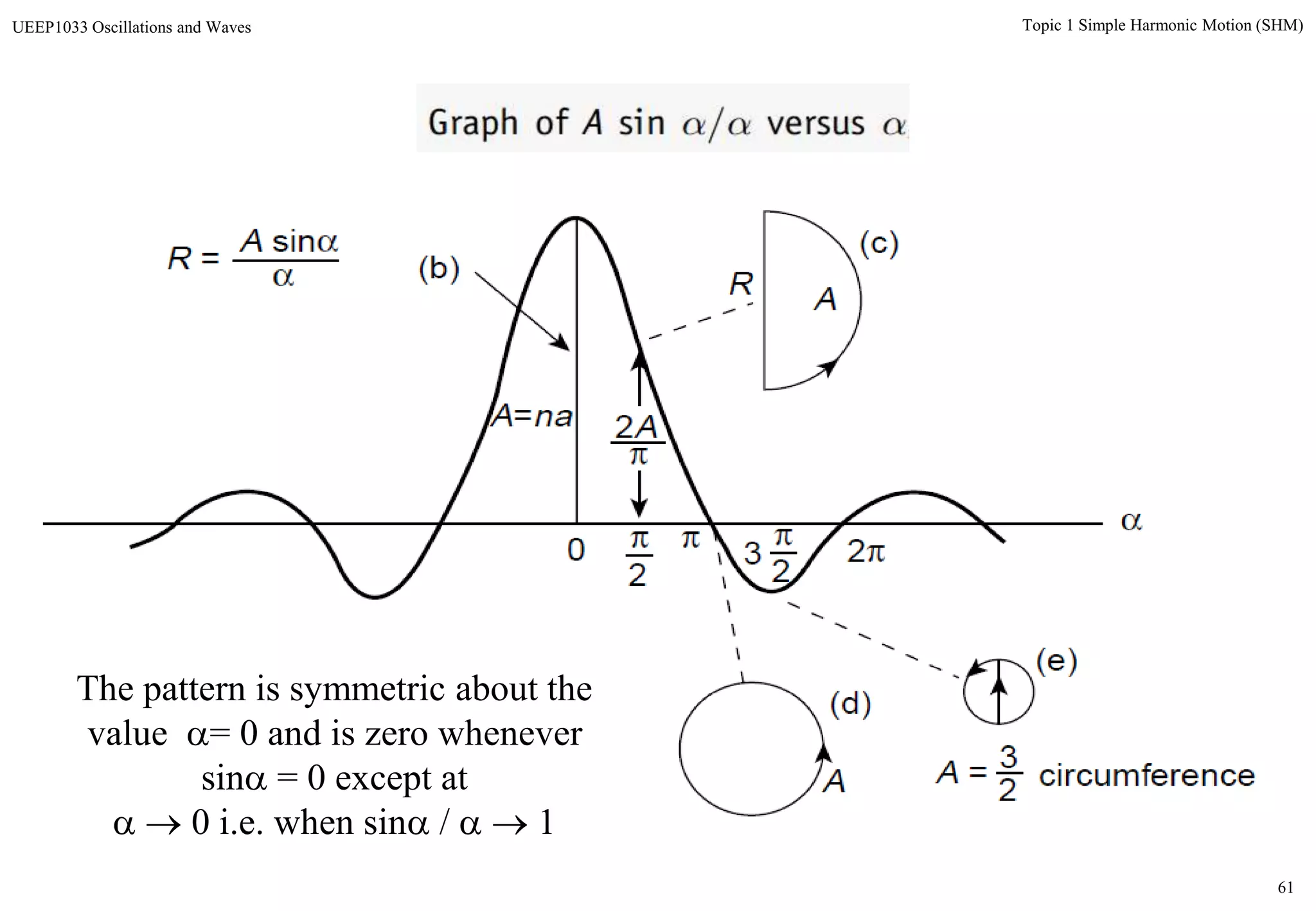
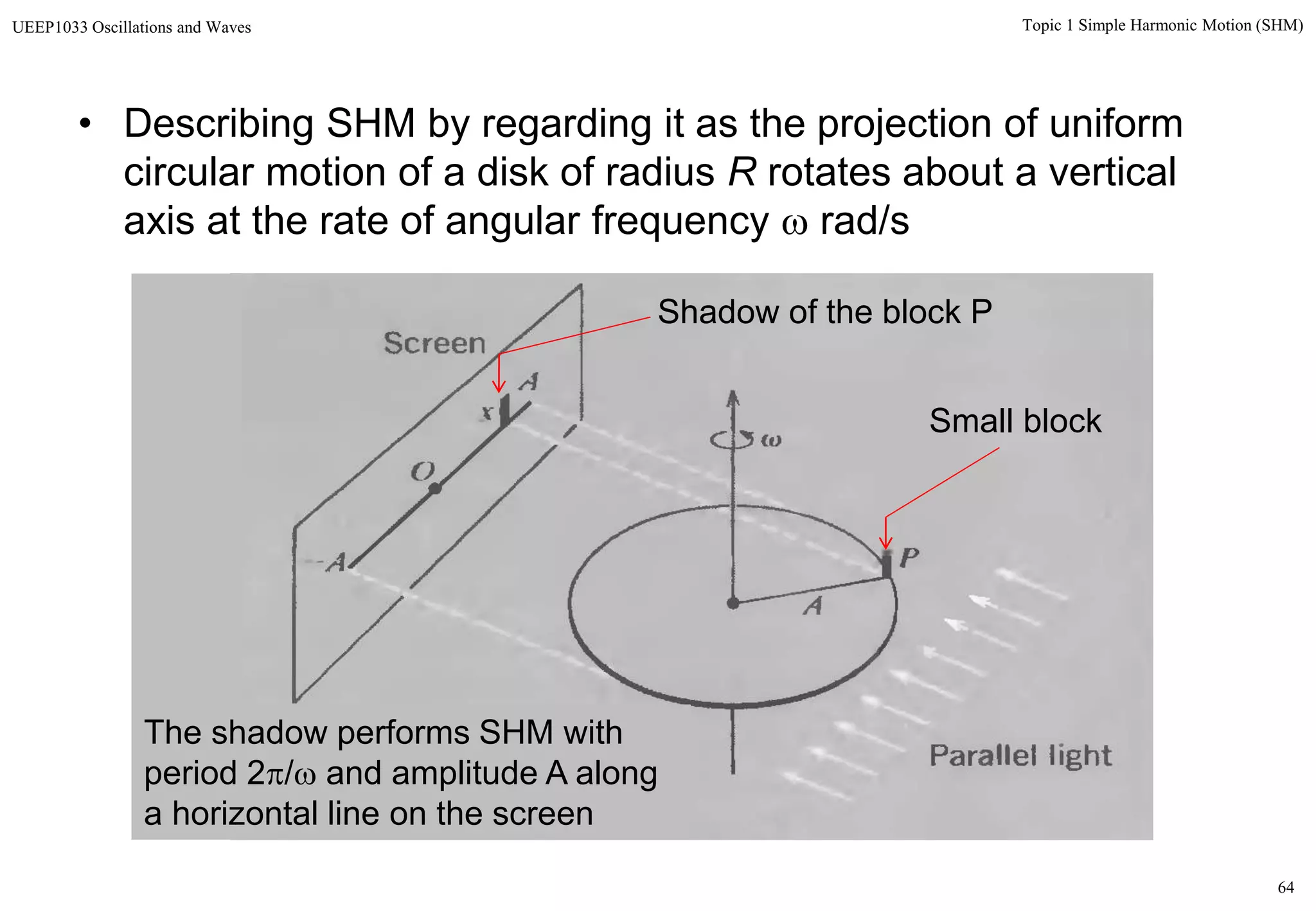
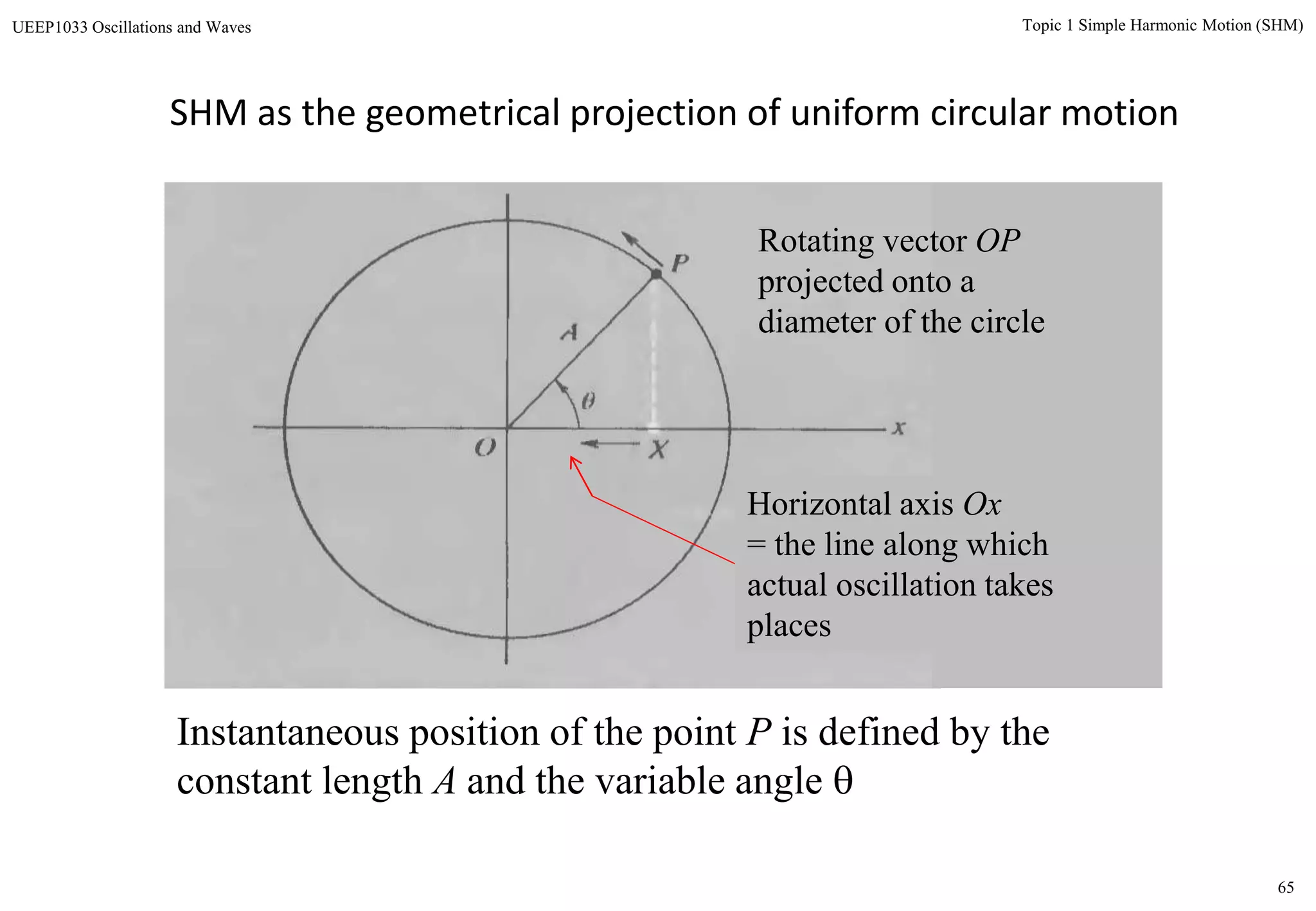
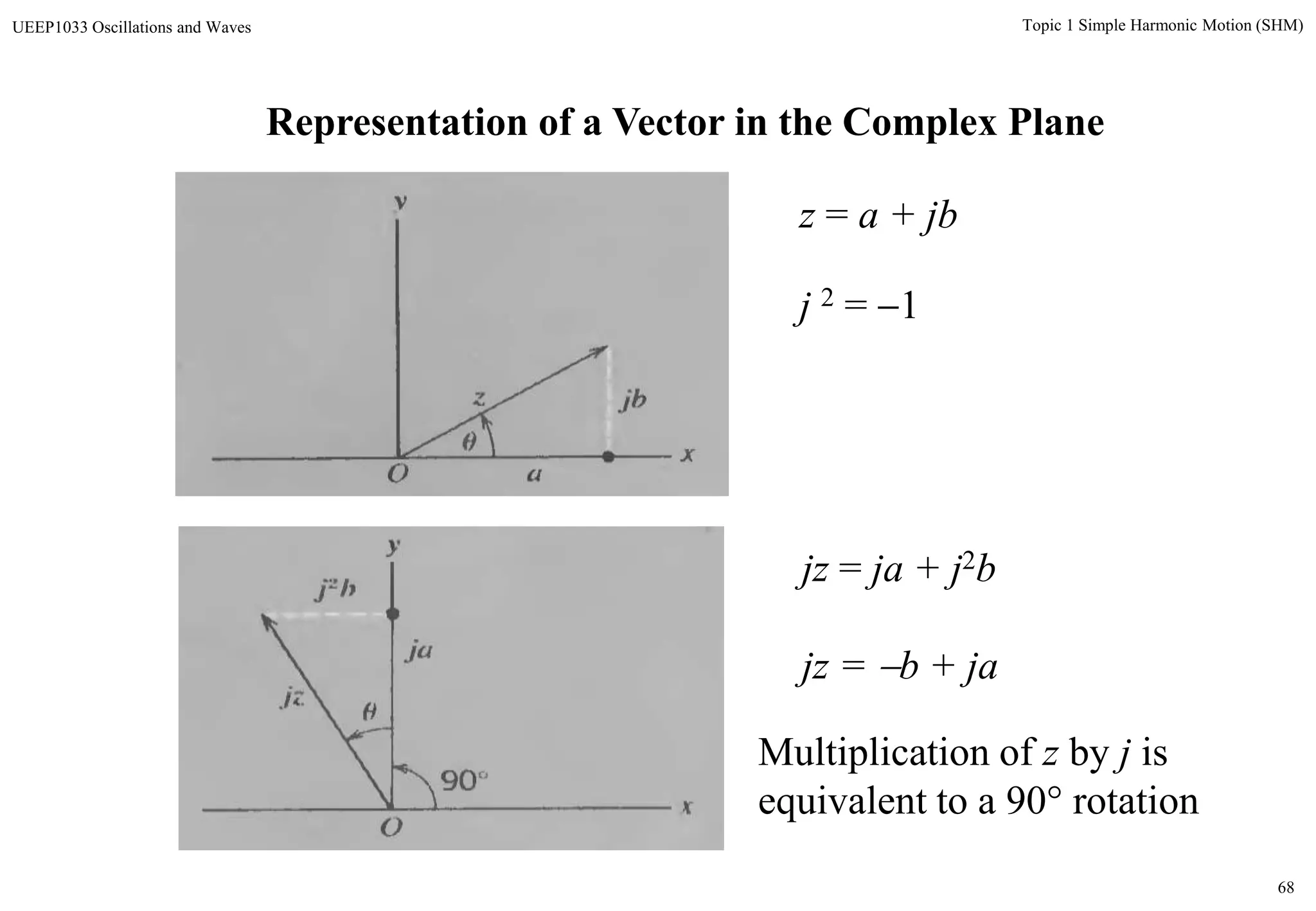
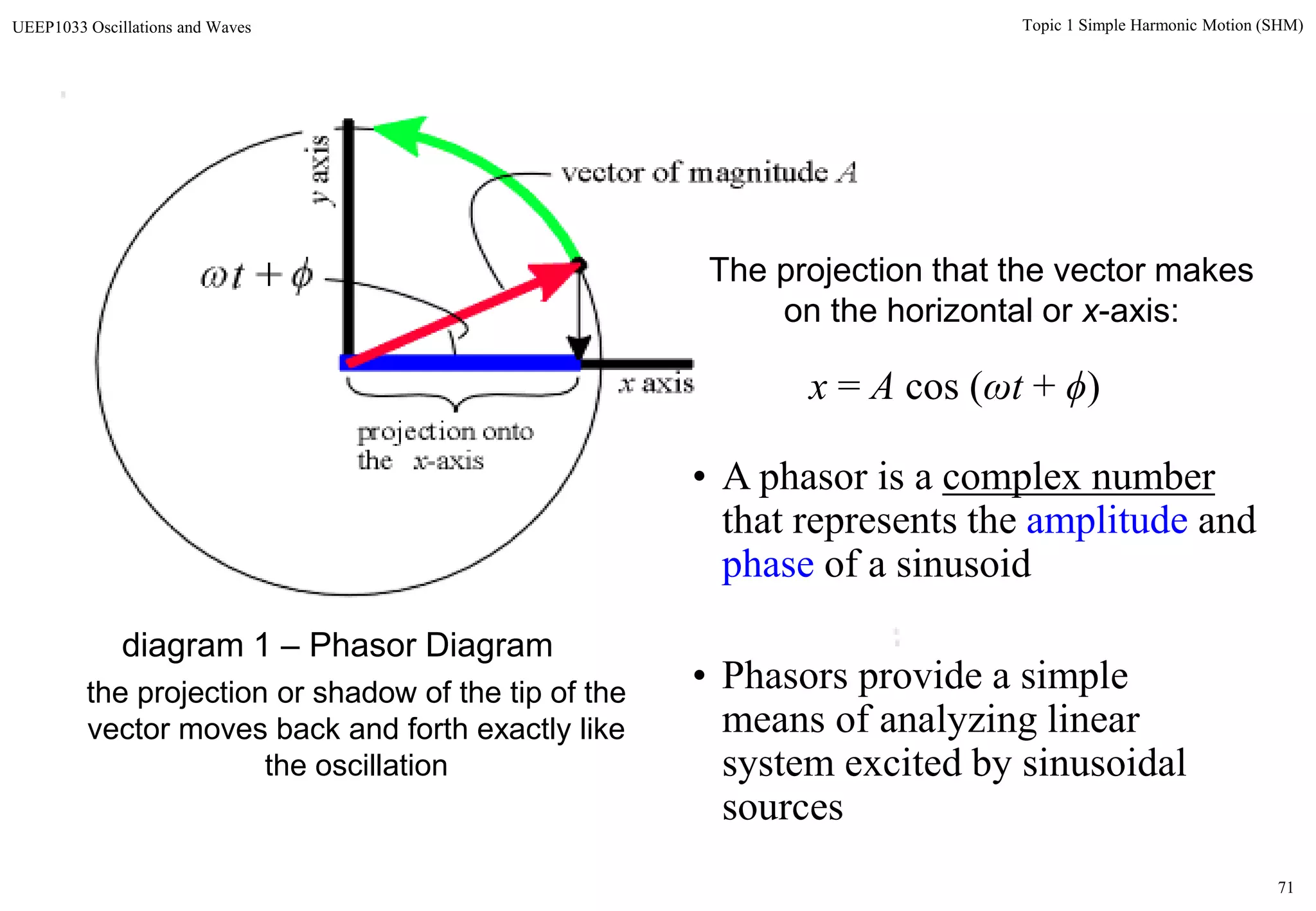
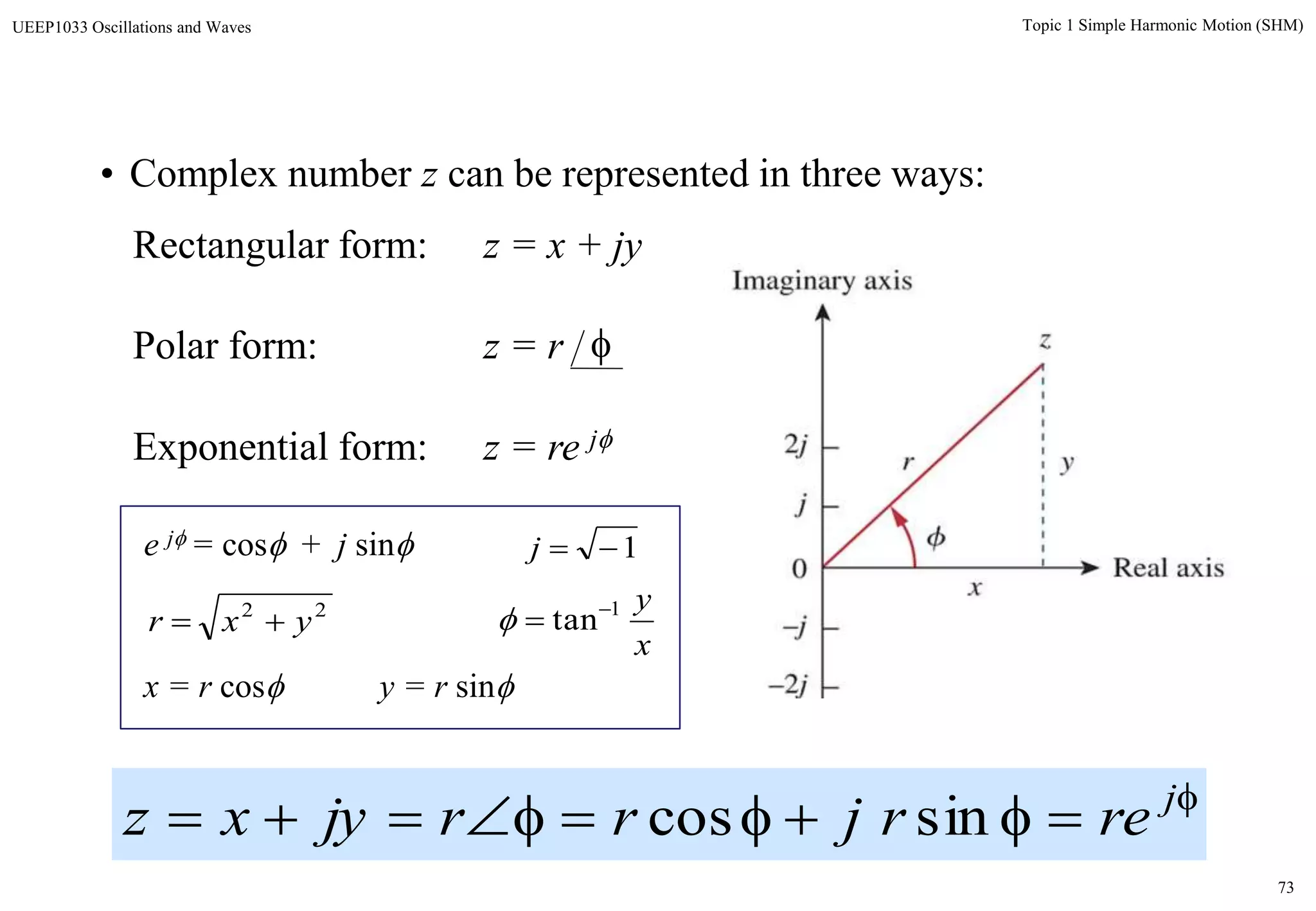
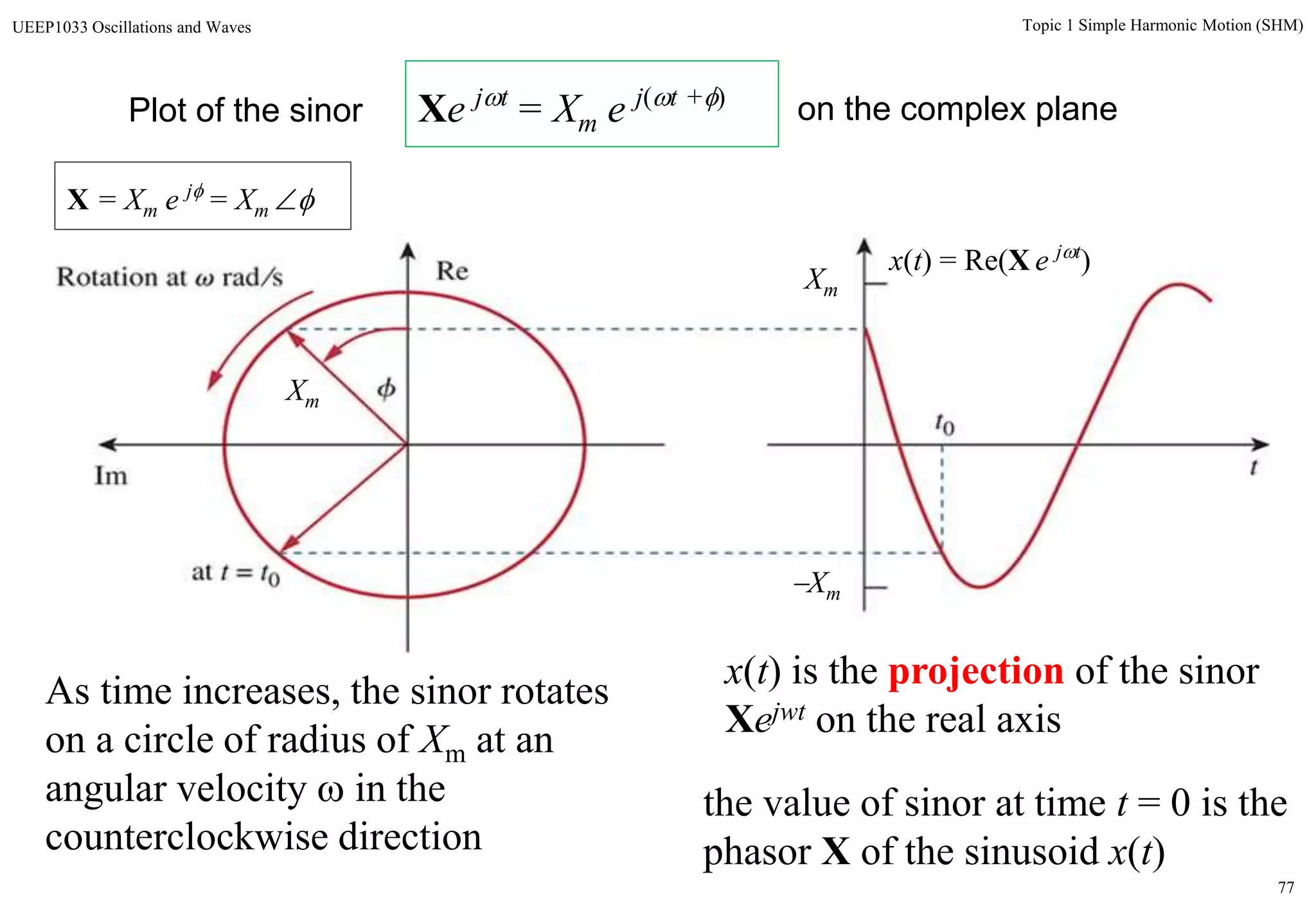
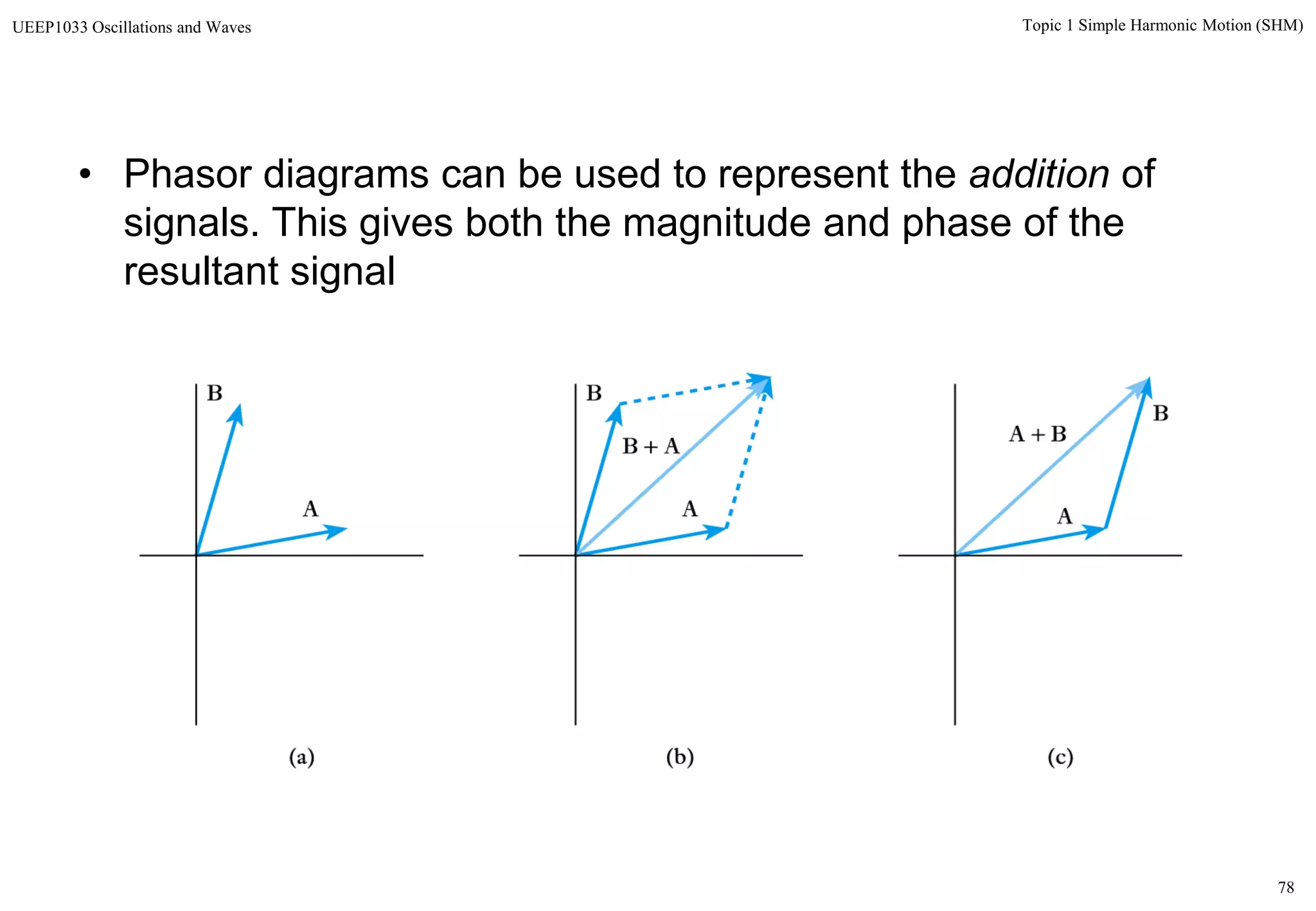
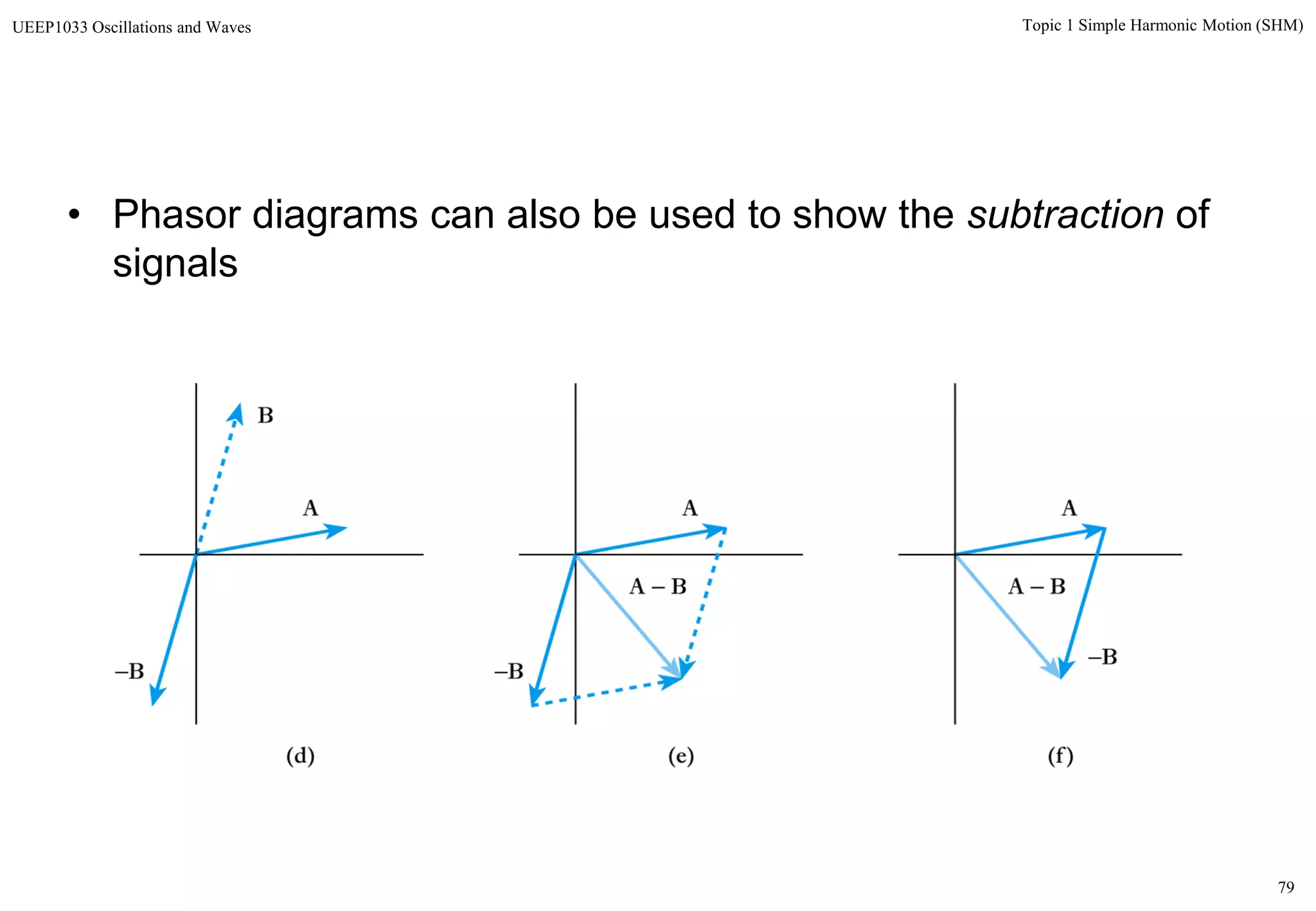
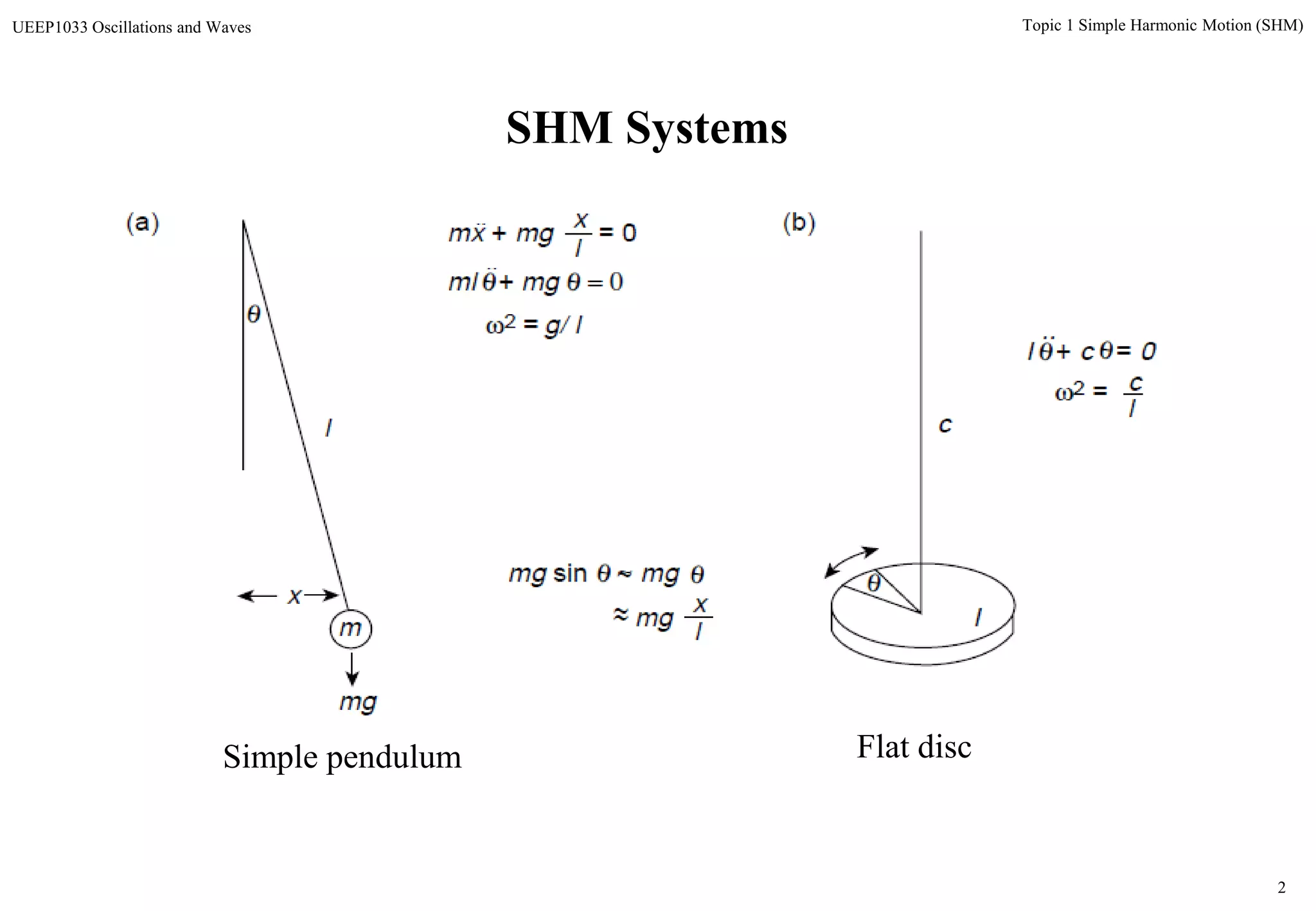
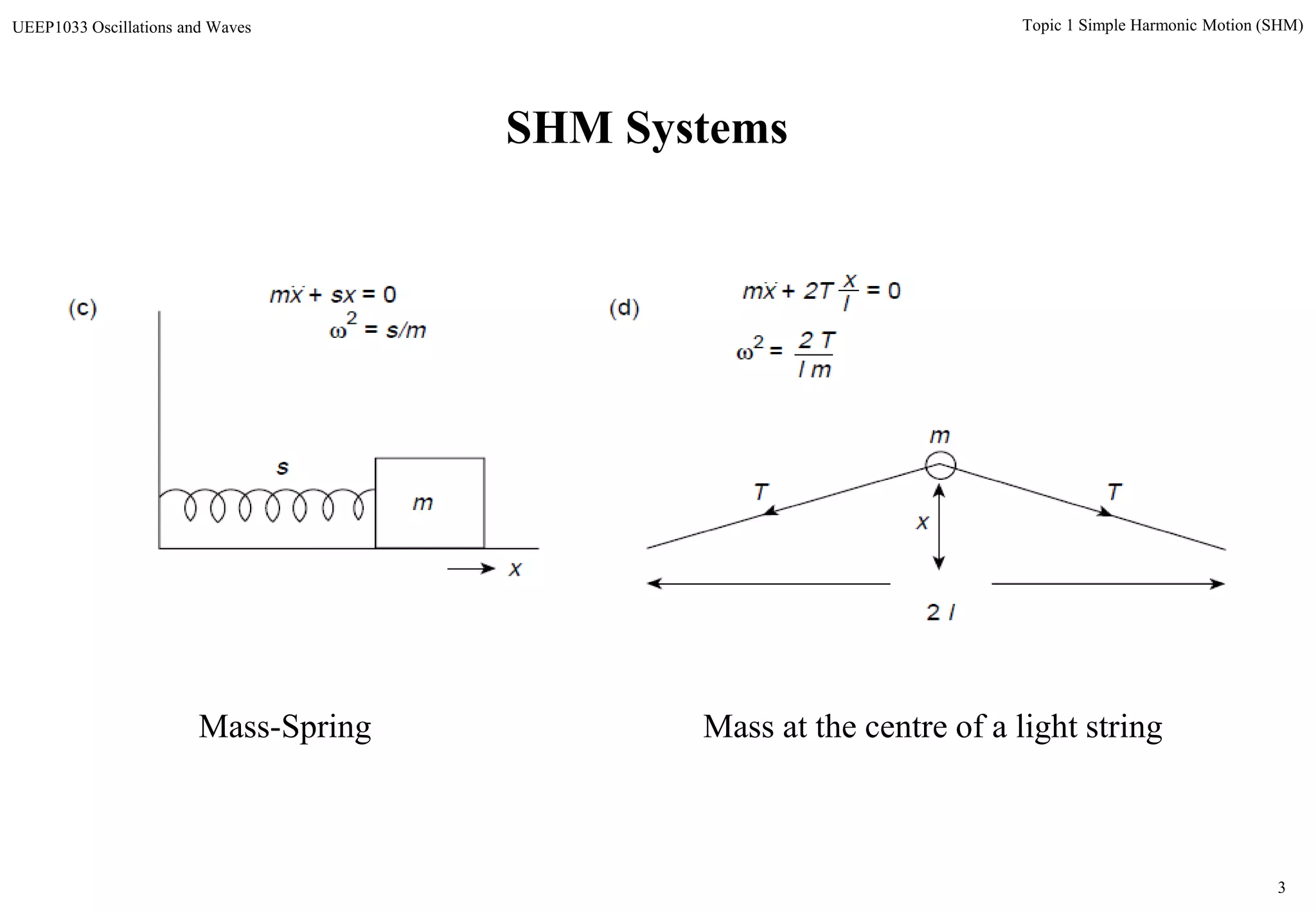
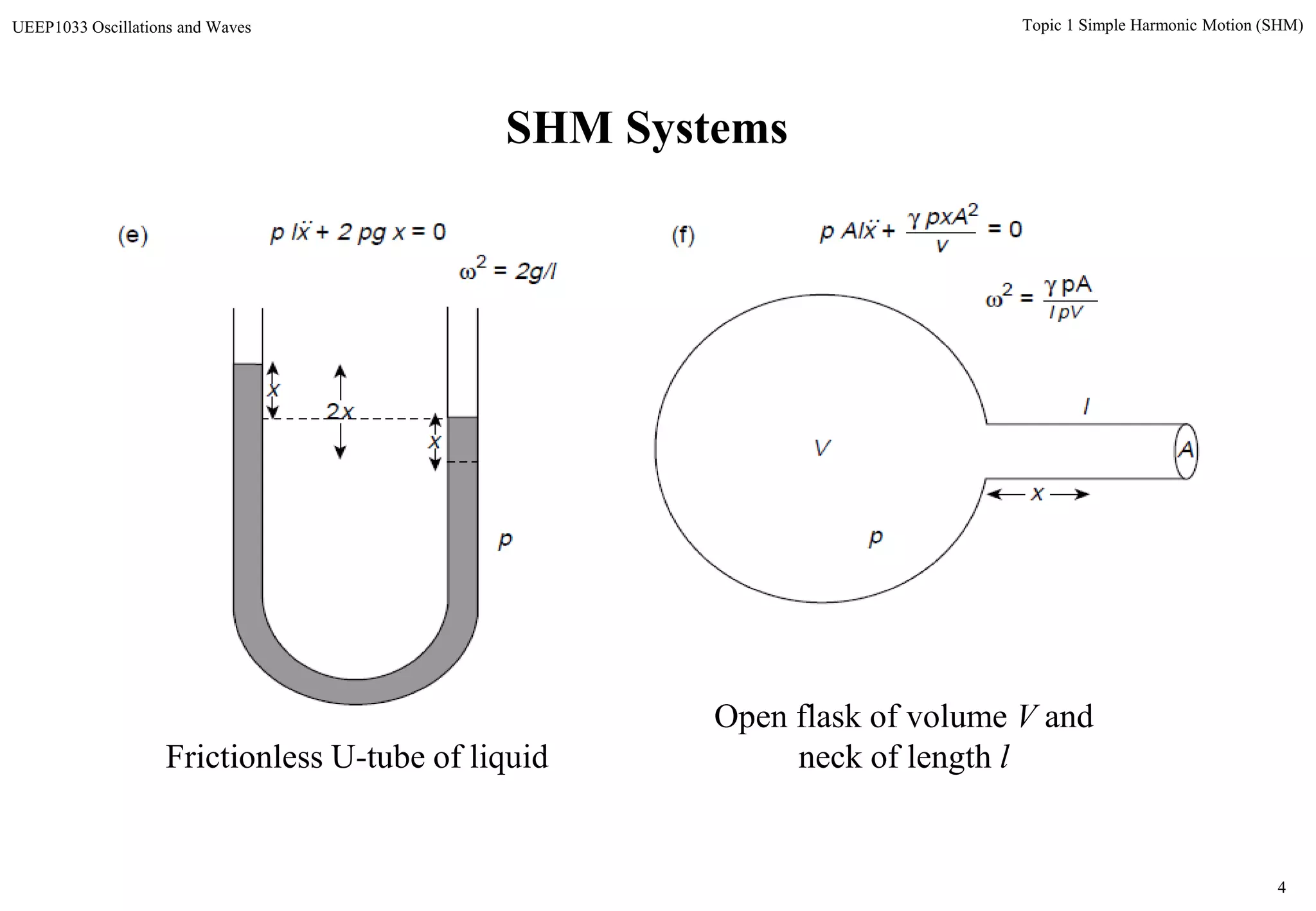
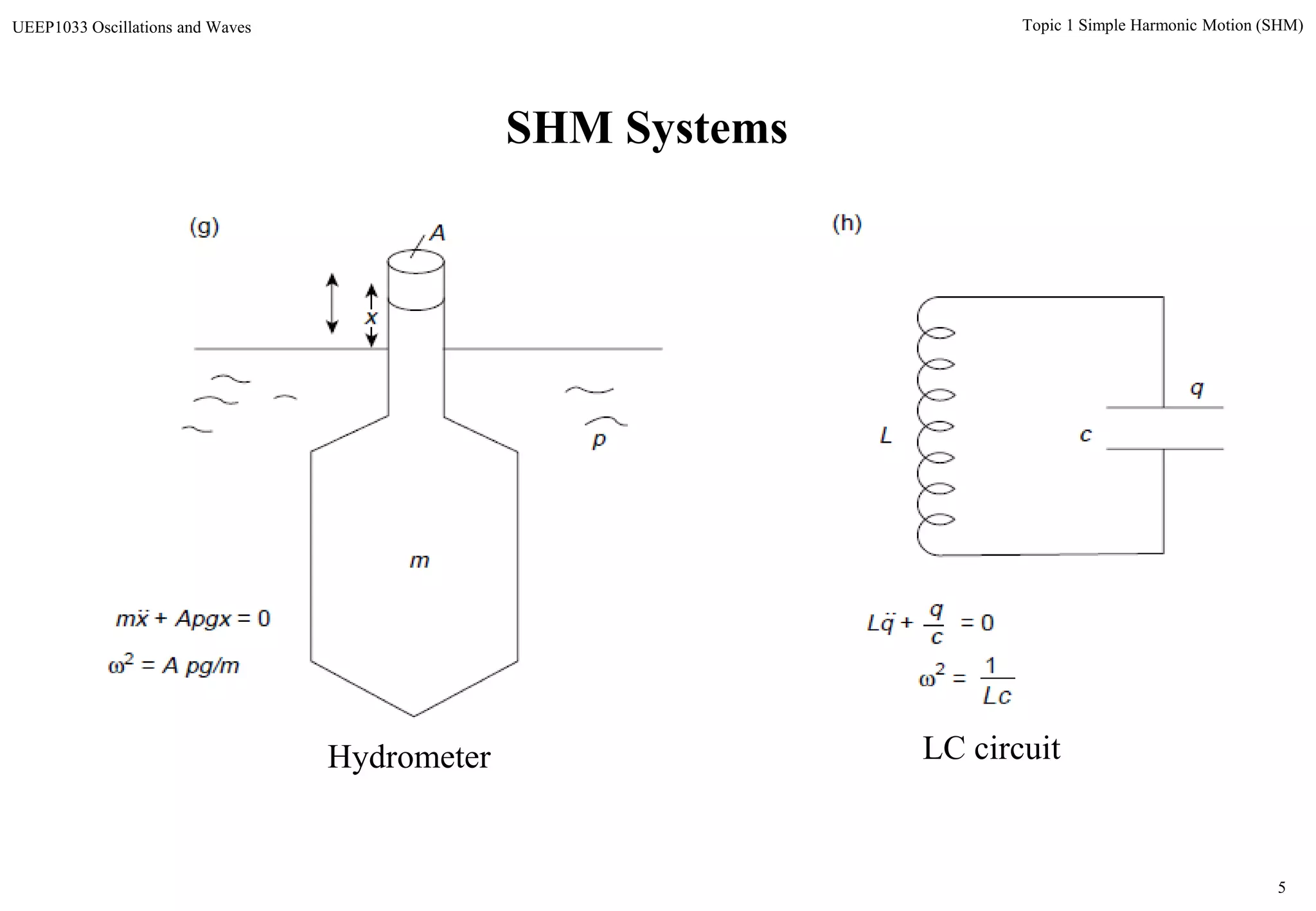
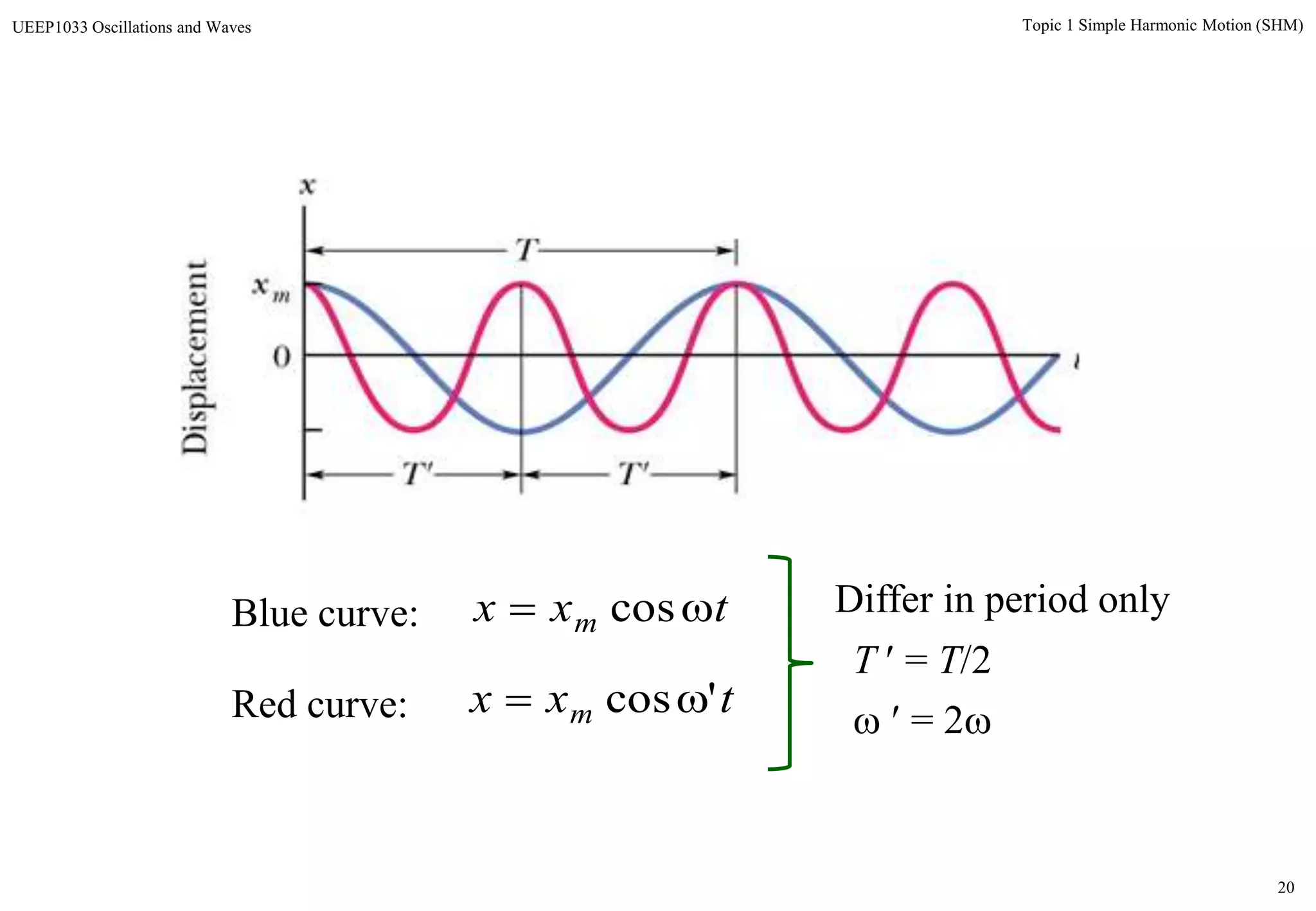
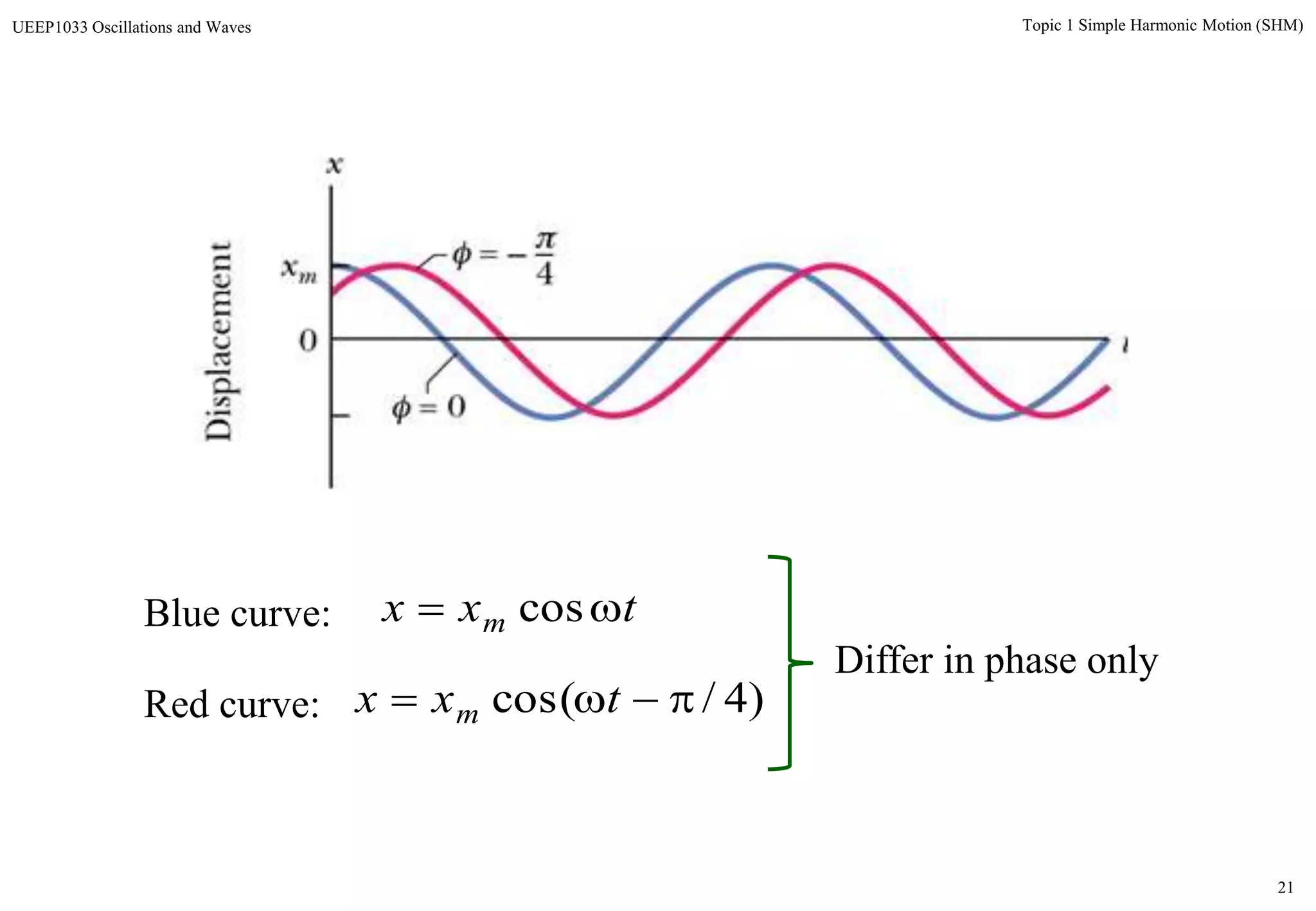
The document discusses simple harmonic motion (SHM) and its characteristics. SHM systems include simple pendulums, mass-spring systems, and others. SHM occurs when a system is slightly displaced from its equilibrium position and experiences a restoring force proportional to the displacement. This results in oscillations where the displacement, velocity, and acceleration vary sinusoidally with time. The energy of a SHM system remains constant as the kinetic and potential energy exchange each cycle.








![13
Topic 1 Simple Harmonic Motion (SHM)UEEP1033 Oscillations and Waves
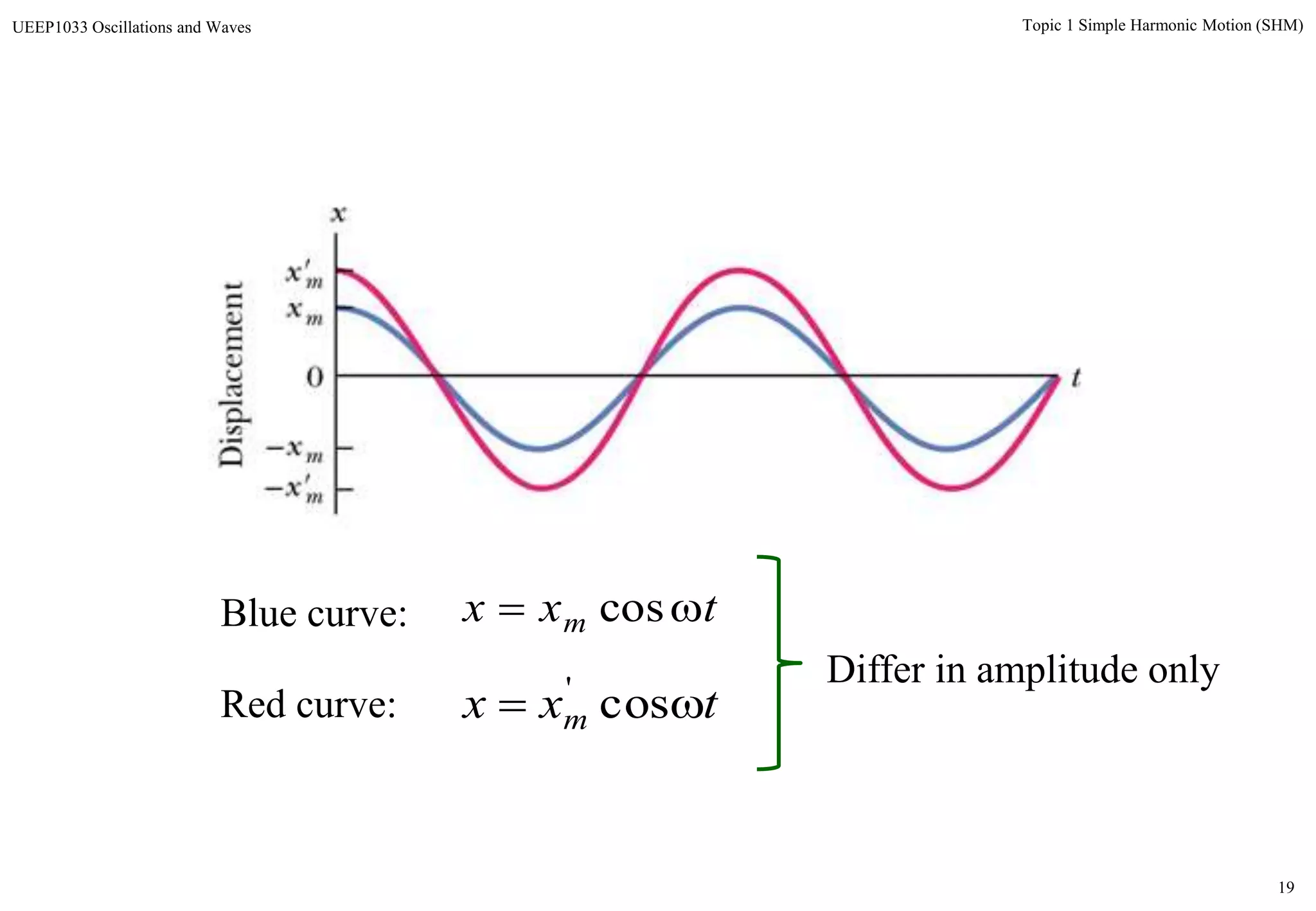
Sinusoidal displacement of simple harmonic oscillator with time,
showing variation of starting point in cycle in terms of phase angle
[source: H.J.Pain, The Physics of Vibrations and Waves 6th Ed. Fig. 1.2]
Displacement In Simple Harmonic Motion (SHM)](https://image.slidesharecdn.com/topic1shm-140705124657-phpapp02/75/Topic-1-shm-13-2048.jpg)


![16
Topic 1 Simple Harmonic Motion (SHM)UEEP1033 Oscillations and Waves
Variation with time of displacement, velocity and acceleration in SHM
[source: H.J.Pain, The Physics of Vibrations and Waves6th Ed. Fig. 1.3]](https://image.slidesharecdn.com/topic1shm-140705124657-phpapp02/75/Topic-1-shm-16-2048.jpg)








![29
Topic 1 Simple Harmonic Motion (SHM)UEEP1033 Oscillations and Waves
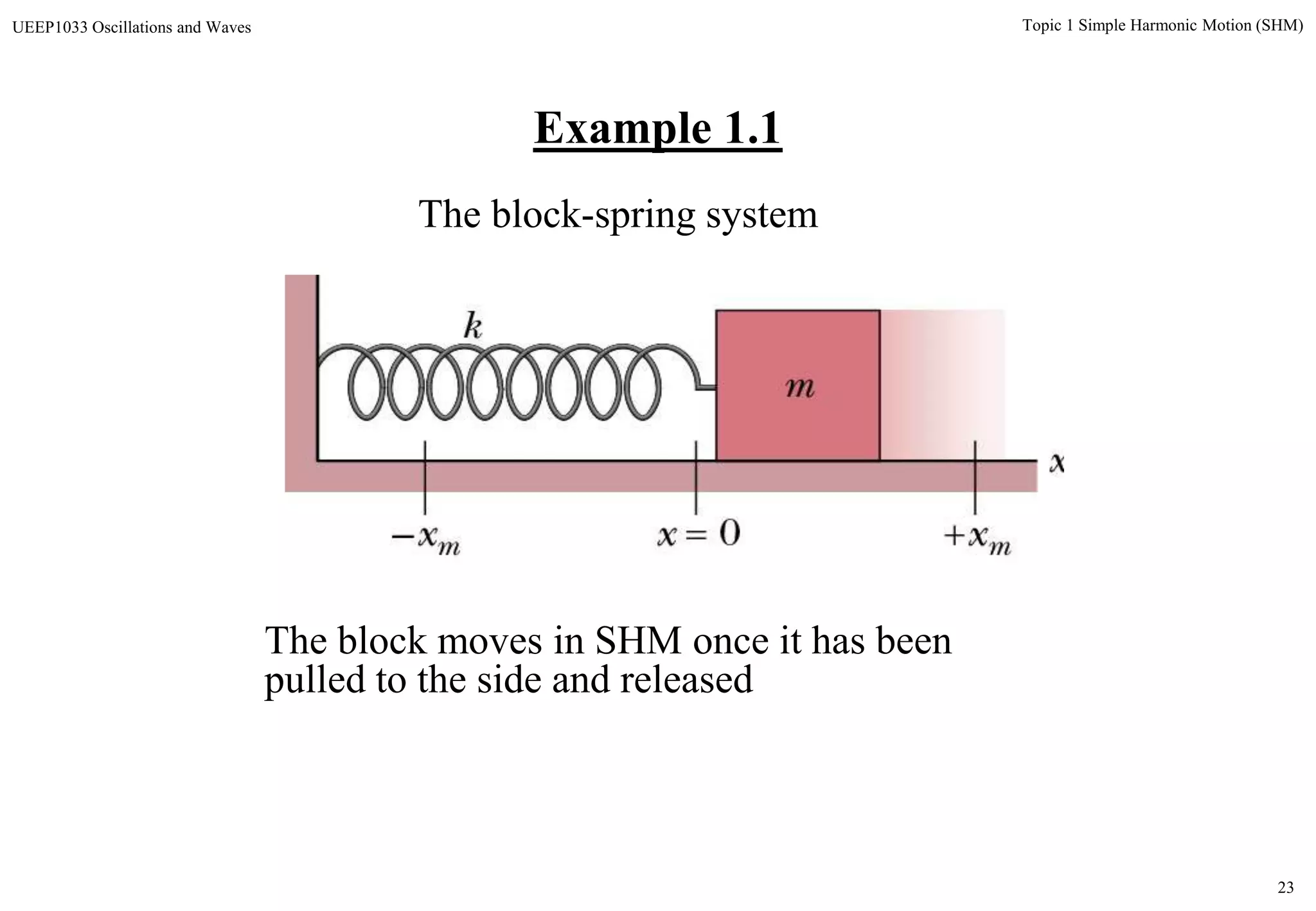
(f) What is the displacement function x(t) for the spring-block
system?
)8.9cos(.11.0)(
])0)rad/s8.9cos([()m11.0()(
ttx
ttx
)cos()( txtx m
Example 1.1 - Solution](https://image.slidesharecdn.com/topic1shm-140705124657-phpapp02/75/Topic-1-shm-29-2048.jpg)