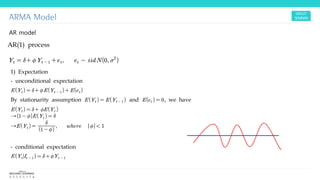
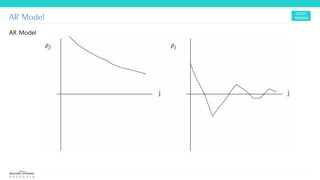
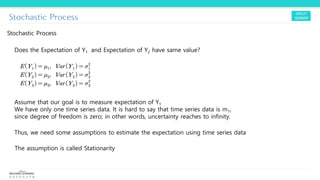
This document provides an overview of time series models and concepts. It discusses stochastic processes, stationarity, the Wold decomposition, impulse response analysis, and ARMA processes. The key points are: 1) Time series models are used to identify shocks and responses over time from stochastic processes. 2) Stationarity assumptions are needed to estimate expectations and variances from time series data using the concept that these values are time-invariant. 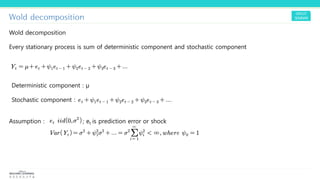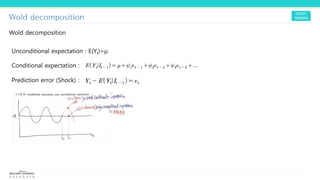3) The Wold decomposition represents a stationary process as the sum of a deterministic component and stochastic prediction errors/shocks. 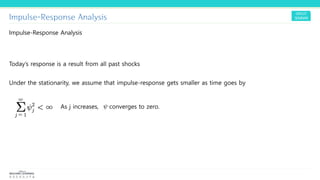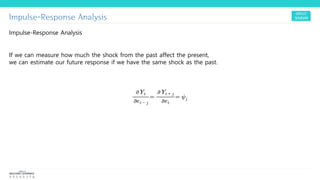4) Impulse response analysis examines how past shocks continue to impact the present and future through their effect over time which decays as time

2. INDEX
01 Time series model
02 Stochas ti c process
03 Stationa rit y
04 Wold decompo si ti o n
05 Impuls e - Re sp o ns e Analysis
06 ARMA Proces s

3. Time series model
Transitory shock Permanent shock
Ex) COVID-19
Activity less -> Demand & investment & Export shrinks
negative aggregated supply shock occurs
Time series
Used to identify shock and response

4. Time series model
Univariate analysis Multivariate analysis

5. Stochastic Process
Stochastic Process
Suppose there are T random variables
Yi(w) is ensemble of Yt
Stochastic Process:
Random variables arrayed through time
Time series data:
Actual data that had occurred

6. Stochastic Process
Stochastic Process
Does the Expectation of Y1 and Expectation of Y2 have same value?
Assume that our goal is to measure expectation of Y1
We have only one time series data. It is hard to say that time series data is m1,
since degree of freedom is zero; in other words, uncertainty reaches to infinity.
Thus, we need some assumptions to estimate the expectation using time series data
The assumption is called Stationarity

7. Stationarity
Stationarity
With no stationarity assumption,
Assuming that expectation and the variance is time invariant is Stationarity
If Expectation and variance of Y1,Y2,….,Yt are same each other, instead of using random variable’s ensemble,
we can estimate expectation and variance using time series data

8. Stationarity
Stationarity
Krodml moment
Cf. random variable W’s moment
1st moment : E(W) : Explains mean of distribution of random variable W
2nd moment : E(W2) : Explains variance of distribution of random variable W
3rd moment : E(W3) : Explains skewness of distribution of random variable W
4th moment : E(W4) : Explains kurtosis of distribution of random variable W
Therefore, it sometimes calls weak stationarity.
If W is vector, 2nd moment is covariance matrix.
So, it also refers to covariance stationarity.

9. Stationarity
Stationarity
Conditional vs Unconditional
Conditional : Forecasting with present and past data
Unconditional : Forecasting with no considering present and past data

10. Wold decomposition
Wold decomposition
Every stationary process is sum of deterministic component and stochastic component
Deterministic component : µ
Stochastic component :
Assumption : ; et is prediction error or shock

11. Wold decomposition
Wold decomposition
Unconditional expectation : E(Yt)=µ
Conditional expectation :
Prediction error (Shock) :

12. Wold decomposition
Wold decomposition
Unconditional expectation : E(Yt)=µ
Conditional expectation :
Prediction error (Shock) :
Conditional variance : = variance of prediction error

13. Impulse-Response Analysis
Impulse-Response Analysis
Today’s response is a result from all past shocks
Under the stationarity, we assume that impulse-response gets smaller as time goes by
As j increases, converges to zero.

14. Impulse-Response Analysis
Impulse-Response Analysis
If we can measure how much the shock from the past affect the present,
we can estimate our future response if we have the same shock as the past.

15. Impulse-Response Analysis
Impulse-Response Analysis
Covariance and Correlation of Yt and Yt-j
What if , Yt=52, Yt-j=48 , Covariance is less than zero.
Then, estimate Yt+j

16. AR Process
Limit of Wold representation
We need to estimate all parameters in the Wold decomposition model.
With finite number of data, it is impossible to estimate infinite number of the parameters.
Thus, approximation is needed.
It is the place where ARMA model comes in.

17. ARMR Model
ARMR Model

18. ARMA Model
Persistance
rj: Auto-correlation
If rj=0 for every j , i.e. (White-noise)

19. ARMA Model
AR model

20. ARMA Model
AR model

21. ARMA Model
AR model

22. ARMA Model
AR model
To be stationary,
Thus,

23. AR Model
AR Model
Using OLS, we can estimate
Now, transform this AR(1) Model into Wold repredentation.

24. AR Model
AR Model
AR(2) Process
1) Expectation
Under the stationarity, we have

25. AR Model
AR Model
AR(2) Process
2) Auto-correlation
Suppose
Stationarity condition :

26. AR Model
AR Model

27. AR Model
AR Model
3) Impulse-Response Analysis
Let

28. AR Model
AR Model
3) Impulse-Response Analysis