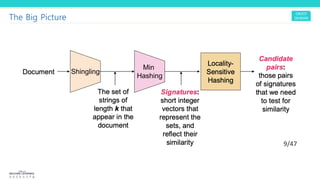
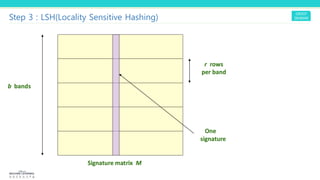
This document summarizes the key steps in the locality sensitive hashing (LSH) algorithm for finding similar documents: 1. Documents are converted to sets of shingles (sequences of tokens) to represent them as high-dimensional data points. 2. MinHashing is applied to generate signatures (hashes) for each document such that similar documents are likely to have the same signatures. This compresses the data into a signature matrix. 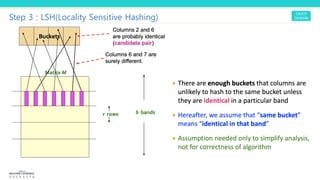3. LSH uses the signature matrix to hash similar documents into the same buckets with high probability, finding candidate pairs for further similarity evaluation and filtering out dissimilar pairs from consideration. This improves the computation efficiency over directly comparing all pairs.

2. Lecture notes of AI506 by Kijung Shin
Introduction

3. Motivation

5. A Common Metaphor
• Many problems can be expressed as finding “similar” sets.
• Find near-neighbors in high-dimensional space.
• Examples :
• Pages with similar words.
• Customers who purchased similar products.
• Images with similar features.

6. Problem for Today’s presentation
• Given :
• High dimensional data points !!, !", … , !#.
• Some distance function $ !!, !"
• Goal :
• Find all pairs of data points (!$, !%) that are within some distance thresh
old $ !$, !% ≤ s.
• Note :
• Time complexity of naïve solution is )(*&).
• Documents are so large or so many that they can’t fit in main mem
ory.

7. The Big Picture

8. Documents as High-Dimensional Data
• Step1 : Shingling
• Convert documents to sets.
• It’s preprocessing stage
• Simple approaches :
• Document ⇒ { words in document }
• Document ⇒ words in document ∖ {meaningless words}
• Don’t work well for this application. Why?
• “Football is more exciting than Baseball” = “Baseball is more exciting than Football”
• Need to account for ordering of words!
• Shingling!

9. Step 1 : Shingling
• A k-shingle for a document is a sequence of k-tokens that appea
rs in the document
• Example : k=2 document D=abcab
• Shingling -> {ab, bc, ca, ab} -> {ab, bc, ca}
• Hash the shingles -> {1, 5, 7} = [1, 0, 0, 0, 1, 0, 1]
• If you worry about order of shingles yet, pich k large enough
• K=5 is OK for short documents

10. Step 2 : Min-hashing
• We just have completed pre-processing
• It remains computational cost problem
• We have N=1,000,000 documents
• =(= − 1)/2 = 5 ∗ 10!! comparisions
• Computation capacity : 10' cmp/sec ⇒ 5 ∗ 10( sec requires = 5 days
• For 10 million, it takes more than a year..
• We need to improve Computation Capacity using Min-hash algo
rithm.

11. Step 2 : Min-hashing
Min-hashing
2 1 2 1
10!×10" input data becomes 1×10" matrix
Signature matrix
Similarity of Columns == Similarity of Signatures
In Probability
So we can save time of comparing two documents
while preserving information of documents in high probability.

12. Step 2 : Min-hashing
• Similarity of two sets : Jaccard distance
• !"# $!, $" =
|$!∩$"|
|$!∪$"|
• ' $!, $" = 1 − !"#($!, $")
• Goal :
To find a hash function ℎ(⋅)such that
• If !"# $!, $" is high, then ℎ $! = ℎ $" in high prob.
• If !"# $!, $" is low, then ℎ $! ≠ ℎ $" in high prob.
Where the function ℎ(⋅) is small enough to fits in RAM

13. Step 2 : Min-hashing
• There is a suitable hash function for the Jaccard similarity :
• Min-Hashing
• ℎ' $ = #"/(:$ ( *!0 1
• F ∶ permutation 1, 2, … , n → {1, 2, … , J}.
• J ∶ the length of shingle dictionary.
• !"#($!, $") = 2' ℎ' $! = ℎ' $"
• If OPQ R!, R" is high, then ℎ R! = ℎ R" in high prob.
• If OPQ R!, R" is low, then ℎ R! = ℎ R" in low prob.
, -

14. Step 2 : Min-hashing
• Proof )
• T = 1, 3, 4, 5, 7 , F ∶ 1, 2,3, 4, 5, 6 , 7 → 1, 2, 3, 4, 5, 6 , 7
• Y. min F T = 1 =
!
(
• ℎ. R! = ℎ. R" ⇔ min
/∶ 1! / 2!
F(!) = min
/∶ 1" / 2!
F(!)
⇔ min
/∶ 1! / 2!
F(!) = min
/∶ 1" / 2!
F(!) ∈ F(R! ∪ R")
!! x1!" !3
x1
+ ,! ≠ + , ∀, ∈ 0"
+ ,# ≠ + , ∀, ∈ 0!
+ , = + 2 for , ∈ 0!, 2 ∈ 0" if and only if ,, 2 ∈ 0! ∩ 0"
Y ℎ. R! = ℎ. R" =
R! ∩ R"
R! ∪ R"

15. Step 2 : Min-Hashing
^ _ 4# 1! 24# 1"
= Y ℎ. R! = ℎ. R" =
R! ∩ R"
R! ∪ R"
= TPQ(R!, R")
Use Monte Carlo Method.

16. Step 3 : LSH(Locality Sensitive Hashing)
• Goal : Find all pairs of data points (14, 15) that are within some di
stance threshold ' 14, 15 ≤ s.
• General Idea of LSH : Find all candidate pairs whose similarity m
ust be evaluated.

17. Step 3 : LSH(Locality Sensitive Hashing)

18. Step 3 : LSH(Locality Sensitive Hashing)

19. Step 3 : LSH(Locality Sensitive Hashing)
• Case 1 : 5"# $!, $" = 0.8 ! = 0.8 9 = 20 ; = 5
• We want R!, R" to be a candidate pair
• So we want to hash them to at least 1 common bucket
• Y R!, R" PJ `aQQaJ bc`def = 1 − Y R!, R" Jaf PJ `aQQaJ bc`def
= 1 − ∏$ Y `$,!, `$," Jaf PJ `aQQaJ bc`def
= 1 − ∏$(1 − Y `$,!, `$," PJ `aQQaJ bc`def )
= 1 − ∏$(1 − 0.8()
= 1 − 1 − 0.328 "6
= 99.965%

20. Step 3 : LSH(Locality Sensitive Hashing)
• Case 2 : 5"# $!, $" = 0.3 ! = 0.8 9 = 20 ; = 5
• We want to hash R!, R" to NO common buckets
• Y R!, R" PJ `aQQaJ bc`def = 1 − Y R!, R" Jaf PJ `aQQaJ bc`def
= 1 − ∏$ Y `$,!, `$," Jaf PJ `aQQaJ bc`def
= 1 − ∏$(1 − Y `$,!, `$," PJ `aQQaJ bc`def )
= 1 − ∏$(1 − 0.3()
= 1 − 1 − 0.00243 "6
= 4.74%