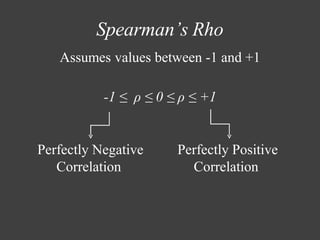
The Spearman rank correlation coefficient is a nonparametric measure of statistical dependence between two variables. It assesses how well the relationship between ranked variables can be described using a monotonic function. The Spearman correlation ranks the data values and then applies the Pearson correlation coefficient to the ranks. It is calculated by finding the differences between the ranks of corresponding data points, squaring these differences, summing them, and normalizing. The Spearman correlation ranges from -1 to 1, with -1 indicating a perfect negative correlation and 1 indicating a perfect positive correlation. Examples are provided to demonstrate calculating Spearman's rho from ranked data and testing for correlation using the test statistic and critical values.

1. Spearman Rank Correlation
A measure of Rank Correlation
Group 3

2. The Spearman Correlation
• Spearman’s correlation is designed to measure
the relationship between variables measured on
an ordinal scale of measurement.
• Similar to Pearson’s Correlation, however it
uses ranks as opposed to actual values.

3. Assumptions
• The data is a bivariate random variable.
• The measurement scale is at least ordinal.
• Xi ,Yi is independent of Xj ,Yj where i ≠ j

4. Advantages
1. Less sensitive to bias due to the effect of
outliers
- Can be used to reduce the weight of outliers (large distances get
treated as a one-rank difference)
4. Does not require assumption of normality.
6. When the intervals between data points are
problematic, it is advisable to study the
rankings rather than the actual values.

5. Disadvantages
1.Calculations may become tedious. Additionally
ties are important and must be factored into
computation.

6. Steps in Calculating Spearman’s Rho
1. Convert the observed values to ranks
(accounting for ties)
2. Find the difference between the ranks, square
them and sum the squared differences.
3. Set up hypothesis, carry out test and conclude
based on findings.

7. Steps in Calculating Spearman’s Rho
1. If the null is rejected then calculate the
Spearman correlation coefficient to measure
the strength of the relationship between the
variables.

8. Hypothesis: I
A. (Two-Tailed)
Ho : There is no correlation between the Xs and the Ys.
(there is mutual independence between the Xs and the Ys)
H1 : There is a correlation between the Xs and the Ys.
(there is mutual dependence between the Xs and the Ys)

9. Hypothesis: II
B. (One-Tailed - Lower)
Ho : There is no correlation between the Xs and the Ys.
(there is mutual independence between the Xs and the Ys)
H1 : There is a negative correlation between the Xs and
the Ys.

10. Hypothesis: III
C. (One-Tailed - Upper)
Ho : There is no correlation between the Xs and the Ys.
(there is mutual independence between the Xs and the Ys)
H1 : There is a positive correlation between the Xs and
the Ys.

11. Test Statistic
(Reject using the appropriate Z critical value)
36
1
n2
(n +1)2
(n −1)
For small samples (N < 40):
T=Σdi
2 =Σ[R(Xi) - R(Yi)]2
For large samples:
T −
1
(n3
− n)
Z*
= 16

12. Test Statistic
• In the case of a large sample:

16 36
T ~ N 1
(n3
− n);
1
n2
(n +1)2
(n −1)

13. Decision Rules
A. Two-tailed:
Reject H0 if T≤ Sα/2 or T > S1- α/2 .
Do not reject otherwise.
B. One-tailed - Lower:
Reject H0 if T > S1- α .
Do not reject otherwise.
C. One-tailed- Upper:
Reject H0 if T≤ Sα.
Do not reject otherwise.

14. Spearman’s Rho
In the case of few ties (less than 5% of the sample):
2
N (N 2
−1)
Where di is the difference in the ranks of each pair
and N is the number of pairs
n
6
 i
d
 = 1 − i=1

15. Spearman’s Rho
If there are numerous ties:
2
2
2
2
2
   
  



  
  


 


n

 i=1
i
n

 i=1
i
n
i=1
0.5
 n +1
2

R(y ) − n
0.5
 n +1
2
 
R(x ) −n
 n +1
2
R(xi )R(yi )−n
 =

16. Spearman’s Rho
Assumes values between -1 and +1
-1 ≤ ρ ≤ 0 ≤ ρ ≤ +1
Perfectly Negative
Correlation
Perfectly Positive
Correlation

17. Example 1
The ICC rankings for One Day International (ODI) and
Test matches for nine teams are shown below.
Test whether there is correlation between the ranks
Team Test Rank ODI Rank
Australia 1 1
India 2 3
South Africa 3 2
Sri Lanka 4 7
England 5 6
Pakistan 6 4
New Zealand 7 5
West Indies 8 8
Bangladesh 9 9

18. Example 1
Team Test Rank ODI Rank d d2
Australia 1 1 0 0
India 2 3 1 1
South Africa 3 2 1 1
Sri Lanka 4 7 3 9
England 5 6 1 1
Pakistan 6 4 2 4
New Zealand 7 5 2 4
West Indies 8 8 0 0
Bangladesh 9 9 0 0
Total 20
Answer:
2
 i
d = 20
T =  = 3

19. Example 2
A composite rating is given by executives to
each college graduate joining a plastic
manufacturing firm. The executive ratings
represent the future potential of the college
graduate. The graduates then enter an in-plant
training programme and are given another
composite rating. The executive ratings and the
in-plant ratings are as follows:

20. Graduate Executive rating (X) Training rating (Y)
A 8 4
B 10 4
C 9 4
D 4 3
E 12 6
F 11 9
G 11 9
H 7 6
I 8 6
J 13 9
K 10 5
L 12 9
•
•
At the 5% level of significance, determine if there is a
positive correlation between the variables
Find the rank correlation coefficient if the null is rejected