Uploaded bySetia Pramana
Correlation and Regression Analysis using SPSS and Microsoft Excel
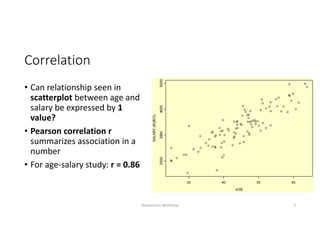
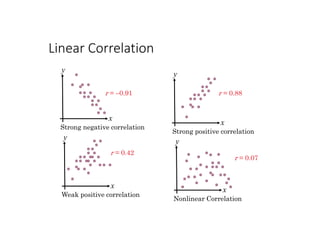
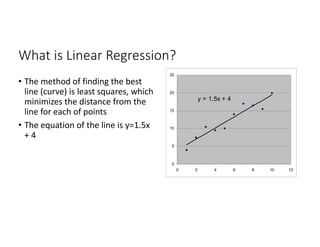
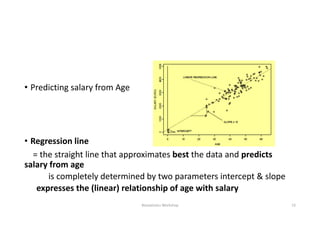
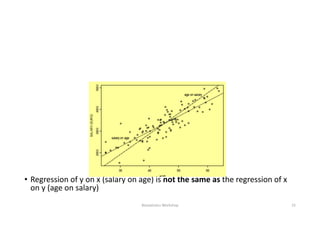
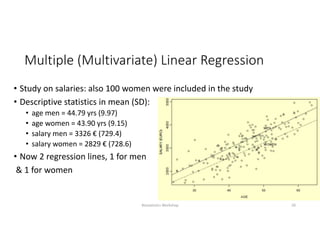
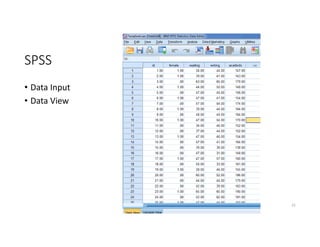
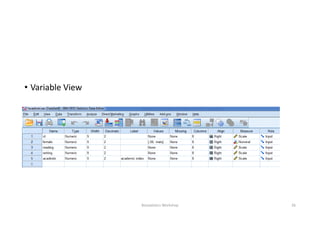
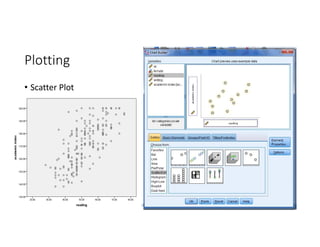
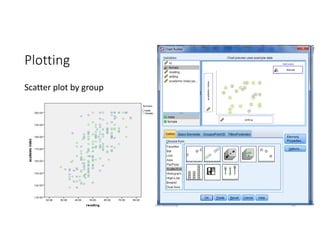
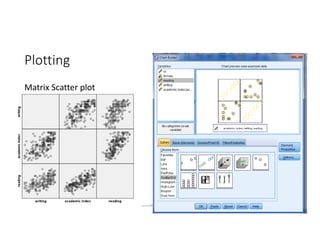
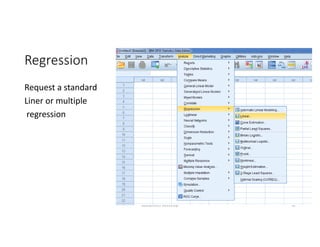
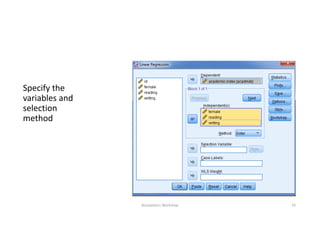
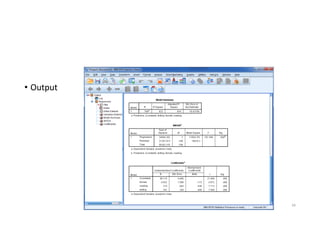
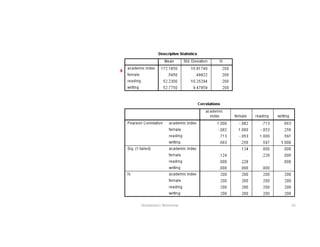
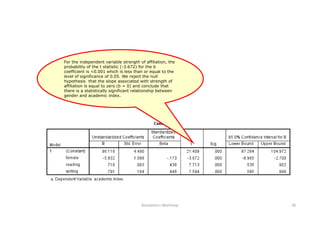
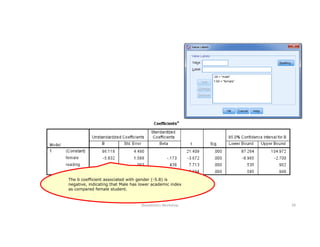
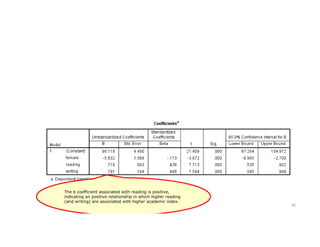
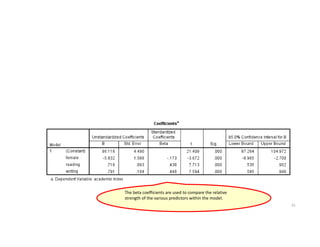
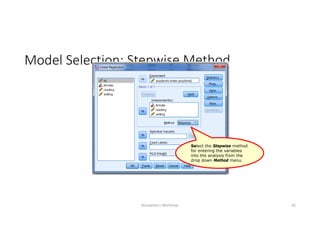
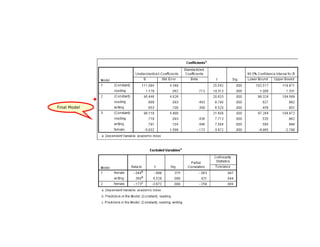
This document discusses correlation and linear regression analysis. It covers correlation coefficients, linear relationships between variables, assumptions of linear regression, and using SPSS and Excel to conduct correlation and regression analyses. Pearson and Spearman correlation coefficients are introduced as measures of the linear association between two continuous variables. Simple and multiple linear regression models are explained as tools to predict an outcome variable from one or more predictor variables.
More Related Content
Similar to Correlation and Regression Analysis using SPSS and Microsoft Excel
Correlation and Regression Analysis using SPSS and Microsoft Excel
- 1.
- 2. Correlation • Express (linear) relationship between 2 continuous measurements x & y by 1 value Examples: length & weight, systolic & diastolic bp • Two methods: •Correlation analysis: symmetric case x & y exchangeable • Regression analysis: asymmetric case predict y from x Biostatistics Workshop 2
- 3. Correlation • Can relationship seen in scatterplot between age and salary be expressed by 1 value? • Pearson correlation r summarizes association in a number •For age‐salary study: r = 0.86 Biostatistics Workshop 3
- 4. Linear Correlation x y Negative Linear Correlation x y NoCorrelation x y Positive Linear Correlation x y Nonlinear Correlation As x increases, y tends to decrease. As x increases, y tends to increase.
- 5. Linear Correlation x y Strong negative correlation x y Weakpositive correlation x y Strong positive correlation x y Nonlinear Correlation r = 0.91 r = 0.88 r = 0.42 r = 0.07
- 6. Correlation • Properties r: • r is unit less •r does not depend on the location & scale of the data • ‐1 < r < 1 • minimal value = ‐1: extreme negative association • maximal value = 1: extreme positive association • special value = 0: no association • And ..... measures linear association! Biostatistics Workshop 6
- 7. Correlation • Pearson correlation coefficient expresses the degree of linear relationship between age and salary • Pearson correlation coefficient is useful when x & y have a Normal distribution •When x or y has not a normal distribution, then: • Try transformation to Normality (log) • Take non‐parametric technique = Spearman rank correlation • When x and y are ordinal, then: • Spearman rank correlation Biostatistics Workshop 7
- 8. Correlation • For Pearson & Spearman correlation x can be interchanged with y without changing the correlation. Hence correlation between age & salary = correlation between salary and age! • Pearson & Spearman correlations only measure association and not causation! •Pearson & Spearman correlation coefficient are often practically equal, but Spearman is more robust to outliers. Biostatistics Workshop 8
- 9.
- 10.
- 11. Simple Linear Regression • Model y = a + b x •Simple: only 1 X • Linear: straight line relationship • Terminology:x: regressor (independent variable) • y: response (dependent variable) • intercept, slope: regression coefficients Biostatistics Workshop 11
- 12. Assumptions of Linear Regression • Linearity • Linear relationship between outcome and predictors •E(Y|X=x)=+ x1 + 2x2 2 is still a linear regression equation because each of the ’s is to the first power • Normality of the residuals • The residuals, i, are normally distributed, N(0, • Homoscedasticity of the residuals • The residuals, i, have the same variance • Independence • All of the data points are independent • Correlated data points can be taken into account using multivariate and longitudinal data methods
- 13.
- 14. • The regression line for the example salary (€) = 200.32 + 69.78 age (yrs) = regression equation •age = 35 average salary = 2642.55 € • age = 50 average salary = 3689.22 € • Prediction without knowing age: Average salary = 3325.712 € • Prediction if age is known (= 38 yrs):Average salary = 2855.521 € Biostatistics Workshop 14
- 15.
- 16. Regression: Slope • The regression line for the example salary (€) = 200.32 + 69.78 age (yrs) = regression equation •age = 50 (mean) salary = 200.32 + 69.78×50 • age = 51 (mean) salary = 200.32 + 69.78×51 • Increase in age with 1 year => Increase in mean salary with 69.78 € • Interpretation of slope = average increase in response when regressor increases with 1 unit Biostatistics Workshop 16
- 17. Coefficient Determination • Gain by knowing relation age with salary • improvement of prediction •improvement can be seen by reduction in variability • Gain can be expressed in 1 value: R2 • R2 : percentage gain by considering regression line. • Example:•R² = 1 ‐ 0.26 = 0.74⇒74% gain by regression model in predicting salary Biostatistics Workshop 17
- 18. Multiple (Multivariate) Linear Regression • The model is: y = b0 + b1 x1 + b2 x2 … + bp xp = multiple linear regression model •multiple: because of p regressors • linear: because of straight line relationship • Terminology: • x1 , x2 , …,xp = regressors (independent variables) • response (dependent variable) y = • b0,b1 , b2 , …,bp = regression coefficients Biostatistics Workshop 18
- 19. Coefficients Regression • There is a univariate effect of regressor/predictor on a response = regression coefficient in simple linear regression = (average) increase of response when regressorincreases with 1 unit • Multiple effect of regressor on response = regression coefficient in multiple linear regression = (average) increase of response when regressor increases with 1 unit and when other regressors are held fixed Biostatistics Workshop 19
- 20. Multiple (Multivariate) Linear Regression • Study on salaries: also 100 women were included in the study • Descriptive statistics in mean (SD): •age men = 44.79 yrs (9.97) • age women = 43.90 yrs (9.15) • salary men = 3326 € (729.4) • salary women = 2829 € (728.6) • Now 2 regression lines, 1 for men & 1 for women Biostatistics Workshop 20
- 21. Multiple (Multivariate) Linear Regression • Two regression lines (estimated separately) • For men: salary = 200.32 + 69.78 age •For women: salary = ‐5.97 + 64.59 age • We see that the intercepts and the slopes are different for men & women. • What does this mean? • Slopes differ = difference between men & women is not constant • Intercepts differ = salary between men & women at age 0 differ? Biostatistics Workshop 21
- 22. Multiple (Multivariate) Linear Regression • Include dummy variable sex • The (overall) model implies two models, one for men and one for women. Namely: •For men: salary = 318.8 + 67 age • For women: salary = 318.8 – 436.5 + 67 age • Thus model assumes that men & women have the same slope in the model. • This means that we assume that the difference between men & women in mean salary is constant on average. Is this so? How can we test this? Biostatistics Workshop 22
- 23. Multiple (Multivariate) Linear Regression • To test that slopes are different for men & women: • Enlarge model again, namely include variable age*sex which is simply the product of age and sex. Thus: •age*sex = 0 for a man age*sex = age for a woman • Fit model with age, sex & age*sex predicting salary • salary = 2000.3 + 69.8 age –206.3 sex – 5.2 age*sex • P‐value for regression coefficient of age*sex = 0.47 • ⇒We do believe that women earn less than men but that the difference is independent of age. Biostatistics Workshop 23
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36. Biostatistics Workshop 36 The MultipleR for the relationship between the set of independent variables and the dependent variable is 0.79, which would be characterized as strong using the rule of thumb than a correlation less than or equal to 0.20 is characterized as very weak; greater than 0.20 and less than or equal to 0.40 is weak; greater than 0.40 and less than or equal to 0.60 is moderate; greater than 0.60 and less than or equal to 0.80 is strong; and greater than 0.80 is very strong. R2 is a statistic that will give some information about the goodness of fit of a model. The R2 coefficient of determination is a statistical measure of how well the regression line approximates the real data points. An R2 of 1 indicates that the regression line perfectly fits the data.
- 37. Biostatistics Workshop 37 The probabilityof the F statistic (107.4) for the overall regression relationship is <0.001, less than or equal to the level of significance of 0.05. We reject the null hypothesis that there is no relationship between the set of independent variables and the dependent variable (R² = 0). We support the research hypothesis that there is a statistically significant relationship between the set of independent variables and the dependent variable.
- 38. Biostatistics Workshop 38 For theindependent variable strength of affiliation, the probability of the t statistic (-3.672) for the b coefficient is <0.001 which is less than or equal to the level of significance of 0.05. We reject the null hypothesis that the slope associated with strength of affiliation is equal to zero (b = 0) and conclude that there is a statistically significant relationship between gender and academic index.
- 39. Biostatistics Workshop 39 The bcoefficient associated with gender (-5.8) is negative, indicating that Male has lower academic index as compared female student.
- 40. Biostatistics Workshop 40 The bcoefficient associated with reading is positive, indicating an positive relationship in which higher reading (and writing) are associated with higher academic index.
- 41.
- 42. Model Selection: Stepwise Method Biostatistics Workshop 42 Select theStepwise method for entering the variables into the analysis from the drop down Method menu.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.