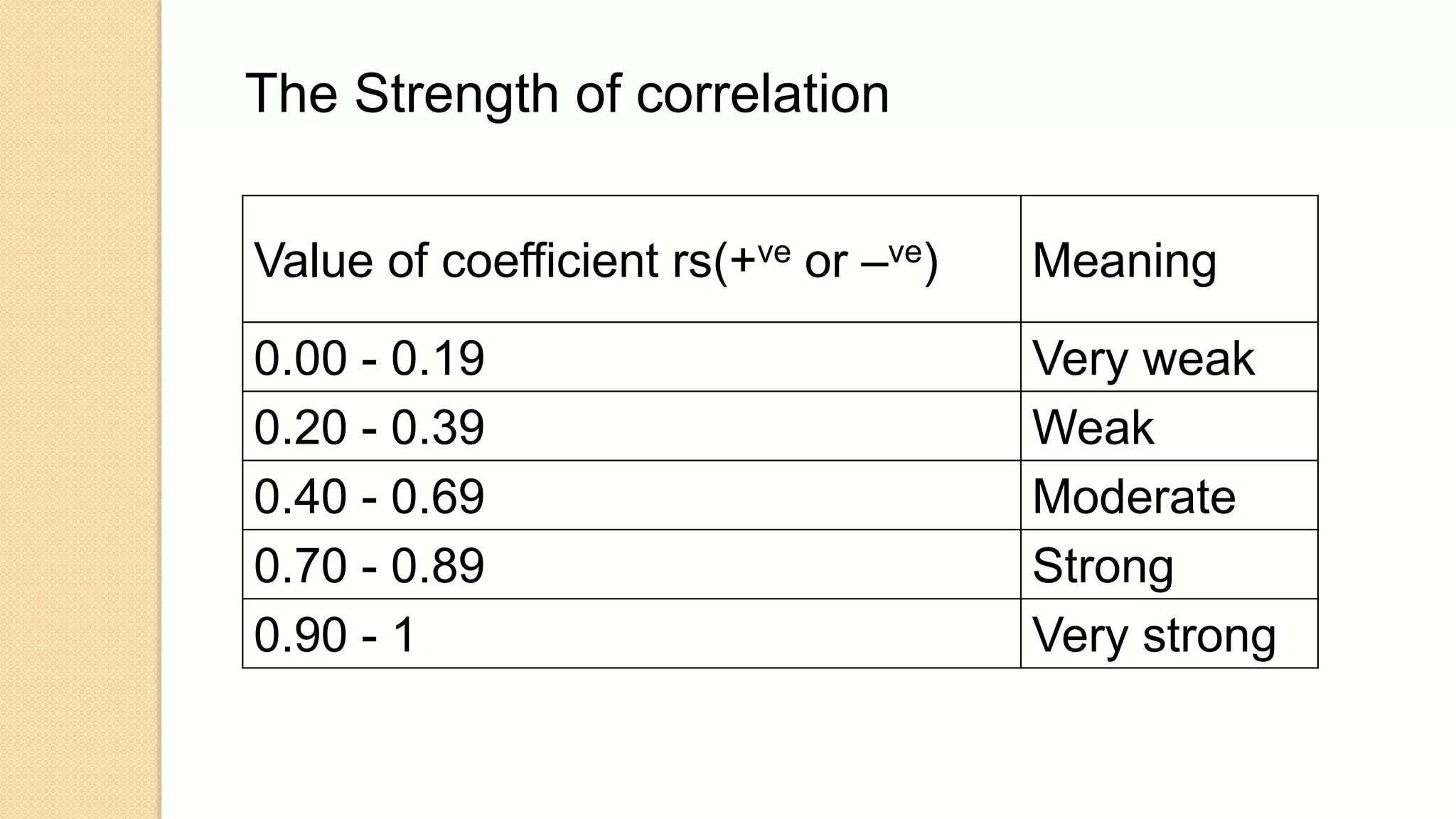
Spearman's rank correlation is a non-parametric measure of statistical dependence between the rankings of two variables. It assesses how well the relationship between two variables can be described using a monotonic function. Unlike Pearson's correlation, Spearman's correlation makes no assumption about the distributions of the variables and is thus suited for both continuous and ordinal data. It is calculated based on the ranked values of the variables rather than the actual values. Spearman's correlation is commonly used in genetics and plant breeding research to identify associations between traits and genes.

1. Spearman’s Rank Correlation
Department of Plant Breeding
and Genetics-2019
IAAS, Tribhuvan University
Kritipur, Kathmandu, Nepal

2. History
 Charles Edward Spearman (1863-1945), an
influential British psychometrician interest to
measure intelligence lead to Spearman’s Rank
Correlation.

3. Problem
Unable to detect and measure intelligence separately
from the specific ability that particular test were
assessing.

4. Mission
To improve statistical methods used to measure
performance and overcome deficiency of scientific
correlation.

5. Outcome
 Proposed several possibilities to measure
correlation.
 Promoted the notion of using ranks instead of actual
measurement.

6.  Pointed the application of Rank correlation in his
paper "The proof and measurement of association
between two things" published in 1907,
 Used as Spearman's Rank Correlation today.
Contd…

7. Introduction
 Spearman Rank's Correlation is a measure of rank
correlation
 statistical dependence between rankings of two
variables

8. Contd…
 denoted by Greek letter rho (ρ) or rs is non-
parametric version of Pearson's correlation.
 is appropriate for both continuous and discrete or
ordinal variables.

9. What actually is non-parametric measure?

10. Features Parametric measure
Non-parametric
measure
Assumptions
Make assumption about
probability distribution of
population under
analysis (mainly normal
distribution)
Don’t make these
assumption so
often called
"distribution free"
method

11. Features Parametric
measures
Non parametric measures
Nature Works with
quantitative data.
work with qualitative
(nominal/ordinal) data
Methods confidence
interval, t-test,
ANOVA, linear
regression etc.
the most common type
being ranked observation

12. Pearson Correlation Vs Spearman’s
Rank correlation

13. Features Pearson’s correlation Spearman Rank
correlation
Definition It is statistical measure
of strength of a linear
relationship between
paired data.
It is statistical measure
of strength of
monotonic relationship
between paired data

14. Features Pearson’s correlation Spearman’s Rank
correlation
Symbol Denoted by r
.
Denoted by rs
Function Calculate relation between
two variables on the basis
of actual data
Calculate association
between two variables
based on the rank.

15. Features Pearson’s correlation Spearman Rank
correlation
Variables used jointly with
normally distributed
variables
used for non-randomly
distributed variables.
Influence of
Outliers
great influence on
Pearson’s correlations
no or very little
influence of outliers on
Rank-based methods

19. Monotonic relationship
 Monotonic function is the one that either never
increase or decrease as its independent variable
increases.
o Monotonically increasing as x variable increases
then y never decreases

20. Contd…
◦ monotonically decreasing as x variable increases,
y variable never increases.
◦ Not monotonic function is the one in which as x
variable increases, the y variable sometimes
decreases and sometimes increases

22. When to use spearman’s rank correlation?
For calculation of Pearson correlation, data must be in
 interval/ratio level,
 linearly related and
 bivariate normally distributed.

23.  If data doesn't meet the assumption it is advisable to
use Spearman's rank correlation to find correlation
between bivariate data

24. Contd…
Assumptions for calculation of Spearman's Rank
correlation
i. Data can be in interval/ratio/ordinal
ii. Monotonically related

25. Value of coefficient rs(+ve or –ve) Meaning
0.00 - 0.19 Very weak
0.20 - 0.39 Weak
0.40 - 0.69 Moderate
0.70 - 0.89 Strong
0.90 - 1 Very strong
The Strength of correlation

26. Association significant or not?
• 0.69 moderate correlation and 0.70 strong correlation????
• Critical value table, the level of significance and strength of
the relationship considered before making assumption on
the association,
• P-value follows a Student’s t-distribution with n-2 degrees of
freedom

27. What about sign?
 rho value ranges from = -1 to +1 .
 Sign of Spearman correlation indicates direction of
association between x (independent variables) and
y (independent variables).

28. Contd…
 If y increases as x increases positive sign and
 if y decreases as x increases then negative sign
 if there is no tendency for y to either increase/
decrease then zero.

29. Calculation of Spearman's rank correlation
 Untied data are those data which do not have same
value.
• Suppose 2 genotype under evaluation has 6 ton/hac
yield then it is called tied data.
• Untied data have unique value.

30. Contd…
For untied data:
𝑟𝑠 = 1 −
6 𝑑𝑖
2
𝑛(𝑛2 − 1)
where, di= difference between two ranks of each
observation
n= number of observation.

31. yield of
genotype
(ton/hac)
stability of
genotype
rank of
yield
rank of
stability
difference
in the
rank
d2
10 7 7 6 1 1
12 8 5 5 0 0
11 6 6 7 -1 1
13 10 4 3 1 1
14 9 3 4 -1 1
15 11 2 2 0 0
16 12 1 1 0 0
So, 𝑟𝑠= 1 −
6 ×4
7 49−1
= 0.92

32. For tied data
If identical value for certain characters, rank is found by
averaging their position in ascending order and using
the same simple formula.

33. yield of
genoty
pe(ton/
hac)
stability
of
genoty
pe
rank of
yield
rank of
stability
differen
ce in
the
rank(di)
di2
10 7 7 6 1 1
12 8 5 4.5 0.5 0.25
11 6 6 7 -1 1
13 10 4 3 1 1
14 8 3 4.5 -1.5 2.25
15 11 2 2 0 0
16 12 1 1 0 0
𝑟𝑠 = 1 −
6 ×5
7 49−1
= 0.901

34. This way of calculating spearman's rank correlation isn't
advocated for tied data so extension of Pearson for ranked
data is used which is given below:
𝜌 =
𝑖 𝑥𝑖 − 𝑥 𝑦𝑖 − 𝑦
𝑖 𝑥𝑖 − 𝑥 2
𝑖 𝑦𝑖 − 𝑦 2
Where, i= paired data

35. Advantages of spearman's rank correlation
 Less sensitive to bias.
 Used to reduce weight of the outliners as large
distance get treated as one rank differences.
◦ Outliers can have great influence on Pearson’s
correlations but have no or very little influence on Rank-
based methods.

36. Contd…
 Doesn't require assumption of normality
 Advisable to study ranking than actual values when
interval between data point are problematic

37. Disadvantages
 Ties are important and must be factored into
computation.
 Correlation doesnot necessarily equal to causation.
 Only indicates whether two variables have a
association

38. Use of Spearman in Genetics and Plant
Breeding
 More efficient in determination of transcriptional
association of genes (whether gene and RNA/protein
are associated or not?)
 Efficient in identifying co-expressed pathway genes
(Kumari et al.)

39. Contd…
 Utilized to analyze association between grain yield
and haplotypes in Genome Wide Association
studies in Rice.( Xie et al.,2015)
 Utilized to find association between traits of interest
and gene/ SNP.

40. Contd…
 Spearman successful in identifying coordinated
transcription factors that control the same biological
processes and traits.

41. Contd…
 Grain yield is positively correlated with the number
of breeding signatures which suggests that
◦ the breeding signatures useful for predicting
agronomic potential
◦ the selected loci may provide targets for rice
improvement. (Xie et al., 2015)

42.  Used in QTL mapping.(Sapkota et al., 2015)
 Spearman ‘s rank correlation can identify more
positive genes and a higher percentage of positive
genes in Arabidopsis(Kumari et al., 2012)
Contd…

43. Conclusion
 Spearman's rank correlation calculates association
between two variables.
 Efficiencies of Spearman's rank correlation vary
with the data properties to some degree and are
largely contingent upon the biological processes and
character under analysis.