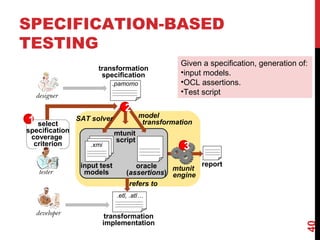
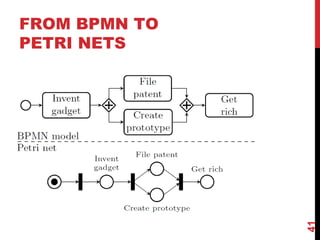
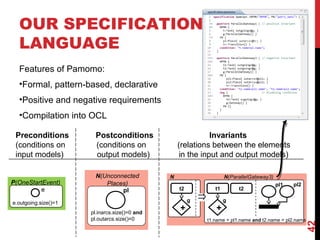
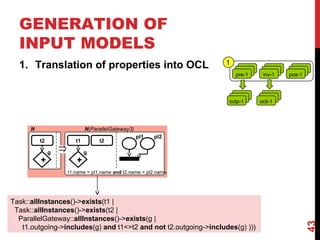
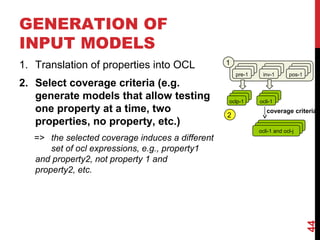
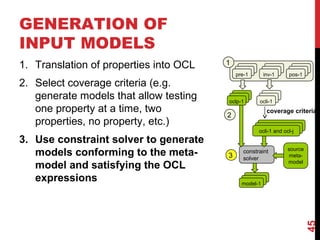
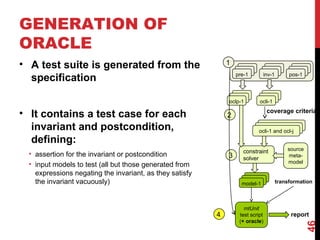
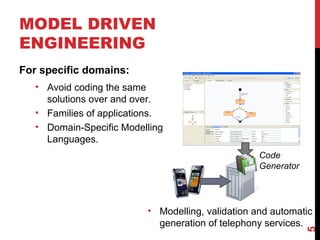
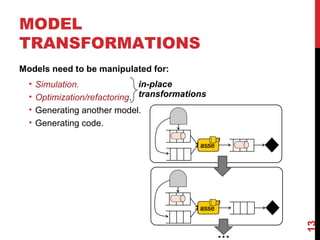
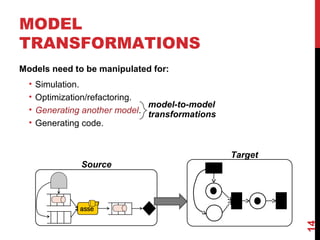
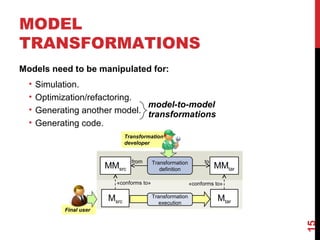
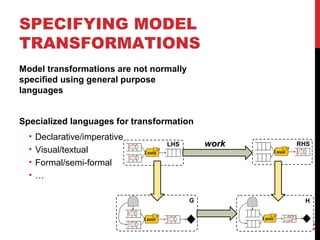
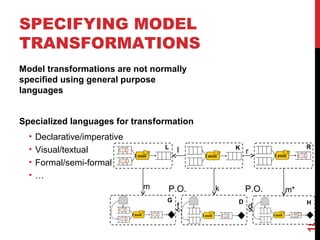
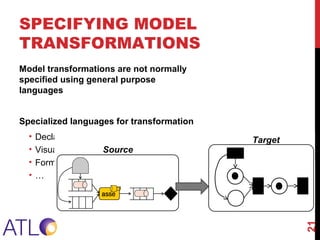
The document discusses model-driven engineering (MDE) as a means to enhance the abstraction level in software development by employing domain-specific models and transformations. It highlights the challenges of testing model-to-model transformations, including the generation of input models and the verification of the correctness of transformations using a specification language called Pamomo. The conclusions point to the need for better validation and verification of MDE artifacts and the ongoing development of tools for transformation testing.

1. PRUEBAS EN EL
DESARROLLO DE
SOFTWARE DIRIGIDO POR
MODELOS
Juan de Lara
(trabajo conjunto con Esther Guerra)
modelling&software engineering
research grouphttp://www.miso.es

2. PRUEBAS DE
TRANSFORMACIONES DE
MODELOS
Juan de Lara
(trabajo conjunto con Esther Guerra)
modelling&software engineering
research grouphttp://www.miso.es

3. Model-Driven Engineering (MDE).
• Meta-Modelling and DSMLs.
• Model Transformations.
Testing model-to-model transformations
Conclusions and Open lines
AGENDA
3

4. DRIVEN
ENGINEERIN
G
Increase the level of abstraction in software
development.
Models are actively used to:
• Describe the problem…
• Simulate/verify/test…
• Generate code for the final application.
Move from the solution space (code-centric) to the
problem space:
• Higher levels of productivity and quality.
• Less accidental details.
4

5. MODEL DRIVEN
ENGINEERING
For specific domains:
• Avoid coding the same
solutions over and over.
• Families of applications.
• Domain-Specific Modelling
Languages.
Code
Generator
• Modelling, validation and automatic
generation of telephony services.
5

6. MODEL DRIVEN
ENGINEERING
For specific domains:
• Avoid coding the same
solutions over and over.
• Families of applications.
• Domain-Specific Modelling
Languages.
• Code generation from State-Machines
for Railway Signaling Systems.
6
Code
generator

7. MetaEdit+
DOMAIN SPECIFIC
MODELLING
LANGUAGES
Describe the structure of the domain
• Relevant primitives and abstractions.
• Relations, features.
• Explicit expert knowledge.
7

8. DOMAIN SPECIFIC
MODELLING
LANGUAGES
DSMLs need not be graphical…
xText
8

9. MODELS AND
META-MODELS
The abstract syntax of DSMLs is
defined through a meta-model
• Classes,
• Attributes,
• Relations.
9
Factory meta-model
Machine
Part
Conveyor
Generator Assembler
inps
outs
*
*
* parts
Terminator
1..*
1..*

10. MODELS AND
META-MODELS
The abstract syntax of DSMLs is
defined through a meta-model
• Classes,
• Attributes,
• Relations.
10
«conforms to»
c1:Conveyor
g:Generator
a:Assembler
c2:Conveyor
c3:Conveyor t:Terminator
p2: Partp2: Partouts
outs
inps
inps
outs inps
Factory meta-model
Machine
Part
Conveyor
Generator Assembler
inps
outs
*
*
* parts
Terminator
1..*
1..*

11. OCL CONSTRAINTS
11
Object Constraint Language
Well-formedness rules, which
every model should satisfy.
Based on First-Order Logic.
g:Generator
«conforms to»
c:Conveyor
Factory meta-model
Machine
Part
Conveyor
Generator Assembler
inps
outs
*
*
* parts
Terminator
1..*
1..*
Factory meta-model
Machine
Part
Conveyor
Generator Assembler
inps
outs
*
*
* parts
Terminator
1..*
1..*
context Generator inv:
self.inps->isEmpty() and self.outs->size()>0
context Generator inv:
self.inps->isEmpty() and self.outs->size()>0
context Terminator inv:
self.outs->isEmpty() and self.inps->size()>0
context Assembler inv:
self.inps->size()>0 and self.outs.size()>0
…
inps

12. MODELS AND
META-MODELS
Models are represented using
concrete syntax
• Visual
• Textual
No need for a 1-1 correspondence
between abstract and concrete
syntax elements.
12
asse

13. MODEL
TRANSFORMATIONS
Models need to be manipulated for:
• Simulation.
• Optimization/refactoring.
• Generating another model.
• Generating code.
in-place
transformations
13
…

14. MODEL
TRANSFORMATIONS
Models need to be manipulated for:
• Simulation.
• Optimization/refactoring.
• Generating another model.
• Generating code.
Source
Target
14
model-to-model
transformations

15. MODEL
TRANSFORMATIONS
Models need to be manipulated for:
• Simulation.
• Optimization/refactoring.
• Generating another model.
• Generating code.
15
MMsrc MMtar
Msrc Mtar
Transformation
definition
from to
«conforms to» «conforms to»
Transformation
execution
Transformation
developer
Final user
model-to-model
transformations

16. MODEL
TRANSFORMATIONS
Models need to be manipulated for:
• Simulation.
• Optimization/refactoring.
• Generating another model.
• Generating code.
16
Template languages
query and
model navigation

17. 17
SPECIFYING MODEL
TRANSFORMATIONS
Model transformations are not normally
specified using general purpose
languages
Specialized languages for transformation
• Declarative/imperative
• Visual/textual
• Formal/semi-formal
• …
LHS RHS
G H
work

18. 18
SPECIFYING MODEL
TRANSFORMATIONS
Model transformations are not normally
specified using general purpose
languages
Specialized languages for transformation
• Declarative/imperative
• Visual/textual
• Formal/semi-formal
• …
L R
G H
K
D
l r
m k m*
f d
P.O. P.O.

19. SPECIFYING MODEL
TRANSFORMATIONS
19
Model transformations are not normally
specified using general purpose
languages
Specialized languages for transformation
• Declarative/imperative
• Visual/textual
• Formal/semi-formal
• …
operation main() { // Epsilon Object Language
…
}
operation Machine work()
{
for (c in self.inps) {
var p : Part := c.parts.random();
c.parts.remove(p);
delete p;
}
for (c in self.outs) c.parts.add(new Part);
}http://www.eclipse.org/epsilon/

20. rule Conveyor2Place {
from c : FAC!Conveyor
to p : PN!Place (tokens <- c.parts->size())
}
Model transformations are not normally
specified using general purpose
languages
Specialized languages for transformation
• Declarative/imperative
• Visual/textual
• Formal/semi-formal
• …
SPECIFYING MODEL
TRANSFORMATIONS
20

21. rule Conveyor2Place {
from c : FAC!Conveyor
to p : PN!Place (tokens <- c.parts->size())
}
Model transformations are not normally
specified using general purpose
languages
Specialized languages for transformation
• Declarative/imperative
• Visual/textual
• Formal/semi-formal
• …
SPECIFYING MODEL
TRANSFORMATIONS
21
Source
Target

22. Model-Driven Engineering (MDE).
Testing model-to-model transformations
• Challenges
• PaMoMo: A specification language for MTs
• Specification-based MT testing
Conclusions and open lines
AGENDA
22

23. TRANSFORMATION
TESTING
CHALLENGES
23
Urgently needed
• we have found 1000+ issues in a repository of ~100 ATL model
transformations (http://www.eclipse.org/atl/atlTransformations/)
Generation of input models
• (very) costly if done manually
• are we testing interesting cases?
Oracle function
• is the result correct?
• syntactically (model conformant to target meta-model)
• semantically (produces the intended model)

24. TRANSFORMATION
TESTING APPROACHES
24
Black box
• Meta-model based:
• Input models derived covering the input meta-model.
• SAT solving/model finding
• Oracle? Random testing: just check for crashes/conformance
• Do the models allow testing all properties of interest?
• Specification (contract) based:
• Input models derived from a high level specification
• The specification serves as oracle
• Specifications for model transformations are still rarely built
(OCL?)
White box
• Look at the transformation logic to generate the tests
• Oracle?

25. A SPECIFICATION LANGUAGE
FOR MODEL TRANSFORMATIONS
PaMoMo: A formal specification language based on algebraic
graph transformation
• Pattern-based, declarative
• Category of graphs and morphisms
• Compilation into OCL for practical purposes
Pre-conditions: (+/-) conditions on input models
Post-conditions: (+/-) conditions on output models
Invariants: relations between input/output models
• Constructive (+)
• Constraining (-)
25

26. CONSTRAINT
GRAPHS (1)
Encoding of (meta-)models
as (typed, attributed) graphs
26
p0: Place
name=“inp
”
tokens=2
t: Transition
in
p1: Place
name=“outp”
tokens=0
name=“tr”
out
p0
t
p1
“inp”
2
“tr”
“outp”
0
in
out
tokens
name
name
name
tokens
Place Transition
in
out
intString
tokensname name
type

27. CONSTRAINT
GRAPHS (2)
Encoding of (meta-)models as
(typed, attributed) graphs
• G= (V, EV, D, ED,
sV: EV → V,
tV: EV → V,
sD: ED → V,
tD: ED → D)
• Plus algebras for data types
Typing as graph homomorphism
• Four commuting functions
27
p0
t
p1
“inp”
2
“tr”
“outp”
0
in
out
tokens
name
name
name
tokens
Place Transition
in
out
intString
tokensname name
type

28. CONSTRAINT
GRAPHS (3)
To express conditions on input/output models, we need:
• Two graphs typed w.r.t source/target meta-models
• Attributes of graphs are variables
• A formula relating variables of both
• C=〈Gs, Gt, α〉
28
p0: Place
name=Y
m: Machine
name=X
X=Y

29. SATISFACTION OF CONSTRAINT
GRAPHS
Satisfaction of constraint graphs is checked by pattern matching
• Finding graph homomorphisms
29
p: Place
p0: Place
name=“inp”
tokens=2
t: Transition
in
p1: Place
name=“outp”
tokens=0
name=“tr”
out
m1={(p, p0)} m2={(p, p1)}

30. SATISFACTION OF CONSTRAINT
GRAPHS
How to relate constraint graphs and graphs?
30
p: Place
p0: Place
name=“inp”
tokens=2
t: Transition
in
p1: Place
name=“outp”
tokens=0
name=“tr”
out
m1={(p, p0)}
tokens=X
X>0

31. SATISFACTION OF CONSTRAINT
GRAPHS
31
p: Place
p0: Place
name=N1
tokens=T1
t: Transition
in
p1: Place
name=N3
tokens=T2
name=N2
out
m1={(p, p0)}
tokens=X
α1 ≡ X>0
α2 ≡ N1=“inp” ∧ T1=2 ∧ N2=“tr” ∧ N3=“outp” ∧ T2=0
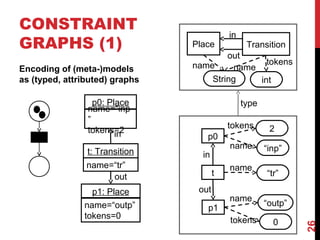
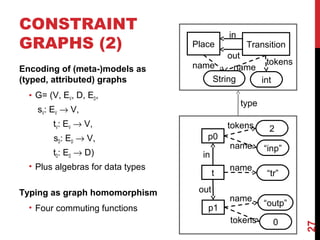
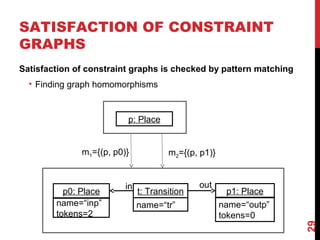
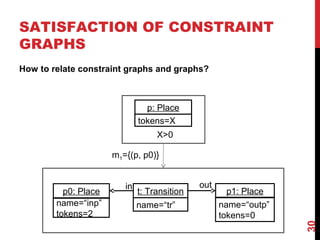
A graph can be seen as a constraint graph
• Constraint graph homomorphism = graph morphism + (reverse)
formula implication (in the example )α2[X/N1]⇒α1

32. Invariants have a bidirectional nature
• Forwards/Backwards satisfaction
32
SATISFACTION OF
INVARIANTS
p0: Place
name=Y
m: Machine
name=X
X=Y

33. Invariants have a bidirectional nature
• Forwards satisfaction
33
SATISFACTION OF
INVARIANTS
m: Machine
name=X
p0: Place
name=Y
m: Machine
name=X
X=Y
m: Machine
name=“m1”
p0: Place
name=“m1”
p1: Place
name=“m2”
∀ ∃

34. Invariants have a bidirectional nature
• Backwards satisfaction
34
SATISFACTION OF
INVARIANTS
p0: Place
name=Y
m: Machine
name=X
X=Y
m: Machine
name=“m1”
p0: Place
name=“m1”
p1: Place
name=“m2”
∀ ∃
p0: Place
name=Y

35. EXAMPLES
35

36. EXAMPLES
36

37. EXAMPLES
37

38. EXAMPLES
38

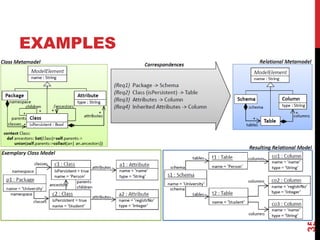
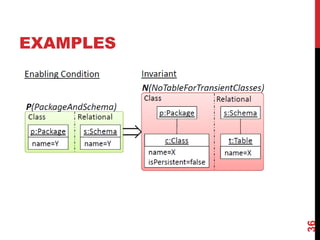
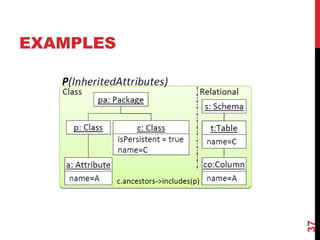
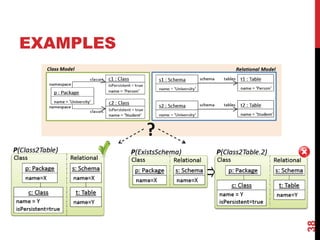
39. WHAT CAN WE DO WITH
AN SPECIFICATION?
Generate “reference” implementations [OGLE09]
• Based on graph transformation
• Terminating, correct, complete
• …but not very efficient
Testing:
• Generation of oracles based on QVT [GL13], OCL [GS15]
• Generation of input models, combining constraints [GS15]
SAT-based refinement checking w.r.t:
• Other specifications, implementations in ATL [BEGL13]
39
[BEGL13] Büttner, Egea, Guerra, de Lara. “Checking Model Transformation Refinement”. ICMT 2013: 158-173
[GL13] Guerra, de Lara, et al. “Automated verification of model transformations based on visual contracts”.
Autom. Softw. Eng. 20(1): 5-46 (2013)
[GS15] Guerra, Soeken. “Specification-driven model transformation testing”. SoSyM 14(2): 623-644 (2015)
[OGLE09] Orejas, Guerra, de Lara, Ehrig. “Correctness, Completeness and Termination of Pattern-Based
Model-to-Model Transformation”. CALCO 2009: 383-397

40. 40
SPECIFICATION-BASED
TESTING
report
select
specification
coverage
criterion
mtunit
script
oracle
(assertions)
input test
models
.xmi
SAT solver model
transformation
transformation
specification
.pamomo
transformation
implementation
.etl, .atl…
refers to
tester mtunit
engine
1
2
3
designer
developer
Given a specification, generation of:
•input models.
•OCL assertions.
•Test script

41. FROM BPMN TO
PETRI NETS
41

42. OUR SPECIFICATION
LANGUAGE
42
Features of Pamomo:
•Formal, pattern-based, declarative
•Positive and negative requirements
•Compilation into OCL
P(OneStartEvent)
e.outgoing.size()=1
e
Preconditions Postconditions Invariants
(conditions on (conditions on (relations between the elements
input models) output models) in the input and output models)
N(Unconnected
Places)
pl.inarcs.size()=0 and
pl.outarcs.size()=0
pl
N
t2
pl2
+
pl1
t1.name = pl1.name and t2.name = pl2.name
N(ParallelGateway3)
t1
g
t2
+
g

43. 43
1. Translation of properties into OCL
GENERATION OF
INPUT MODELS
N
t2
pl2
+
pl1
t1.name = pl1.name and t2.name = pl2.name
N(ParallelGateway3)
t1
g
t2
+
g
Task::allInstances()->exists(t1 |
Task::allInstances()->exists(t2 |
ParallelGateway::allInstances()->exists(g |
t1.outgoing->includes(g) and t1<>t2 and not t2.outgoing->includes(g) )))
pre-1 inv-1
1
pos-1
ocli-1oclp-1

44. 44
1. Translation of properties into OCL
2. Select coverage criteria (e.g.
generate models that allow testing
one property at a time, two
properties, no property, etc.)
=> the selected coverage induces a different
set of ocl expressions, e.g., property1
and property2, not property 1 and
property2, etc.
GENERATION OF
INPUT MODELS
pre-1 inv-1
coverage criteria
1
2
pos-1
ocli-1oclp-1
ocli-1 and ocl-j

45. 45
1. Translation of properties into OCL
2. Select coverage criteria (e.g.
generate models that allow testing
one property at a time, two
properties, no property, etc.)
3. Use constraint solver to generate
models conforming to the meta-
model and satisfying the OCL
expressions
GENERATION OF
INPUT MODELS
pre-1 inv-1
coverage criteria
1
2
pos-1
ocli-1oclp-1
ocli-1 and ocl-j
constraint
solver3
model-1
source
meta-
model

46. 46
• A test suite is generated from the
specification
• It contains a test case for each
invariant and postcondition,
defining:
• assertion for the invariant or postcondition
• input models to test (all but those generated from
expressions negating the invariant, as they satisfy
the invariant vacuously)
GENERATION OF
ORACLE
pre-1 inv-1
coverage criteria
1
2
pos-1
ocli-1oclp-1
ocli-1 and ocl-j
constraint
solver3
model-1
source
meta-
model
mtUnit
test script
(+ oracle)
4
transformation
report

47. TOOL SUPPORT
47
generationgeneration
PAMOMO
•EMF-based tool.
•Textual/visual syntax for patterns.
•Generation of input models
and test scripts.
•Model generation by using
the USE solver.
mtUnit
•EMF-based tool.
•Automates transformation testing.

48. Model-Driven Engineering (MDE).
Testing model-to-model transformations
Conclusions
AGENDA
48

49. CONCLUSION
S
MDE: increase the level of abstraction in software
development by the use of (domain-specific) models.
V&V of the different MDE artefacts (meta-models,
transformations, code generators)
Model transformation testing:
• Generation of input models
• Oracle function
A specification language like PaMoMo can be used
for both
49

50. CURRENT LINES
Static analysis of (ATL) model transformations
• Type inference
• Quick fixes
DSLs for model mutation
• Primitives to generate mutants of models conformant to
arbitrary meta-models
• Transformations are also models
Model transformation reuse
• Transformations used with different meta-models they
were initially built
50

51. THANKS!
Questions?
51
http://www.miso.es
Juan.deLara@uam.es
modelling&software engineering
research group