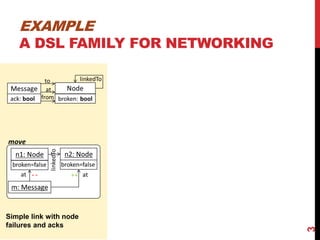
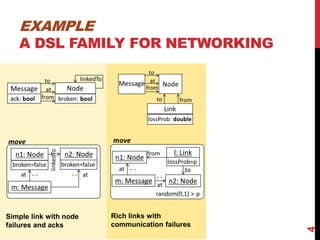
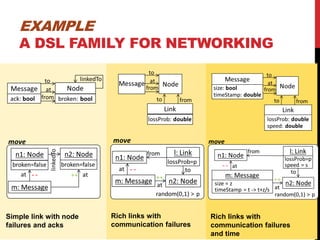
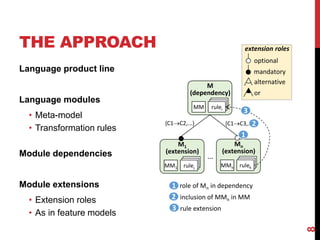
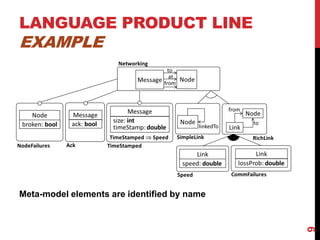
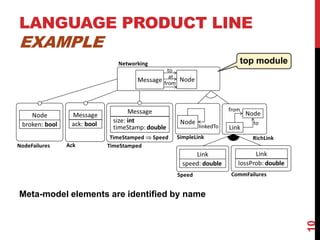
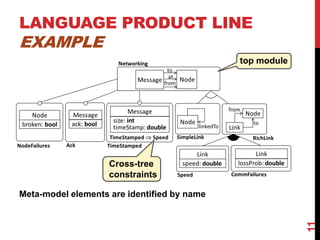
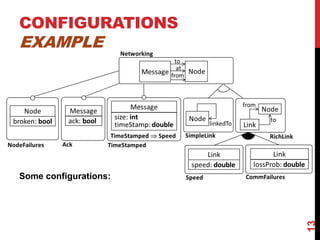
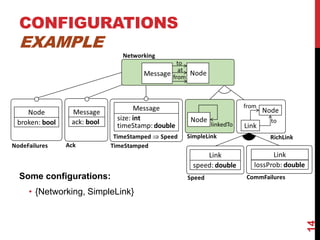
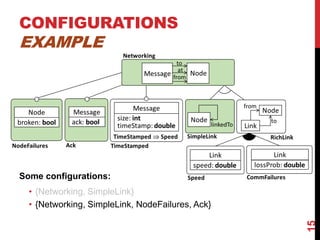
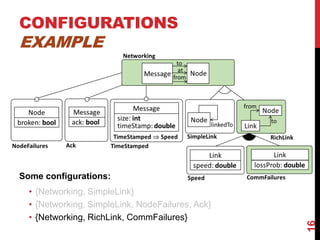
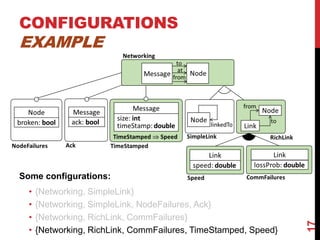
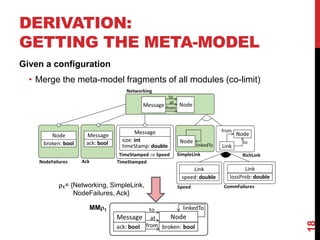
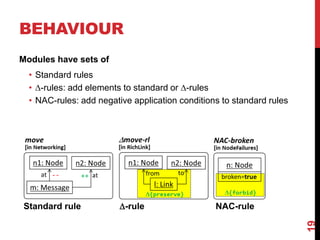
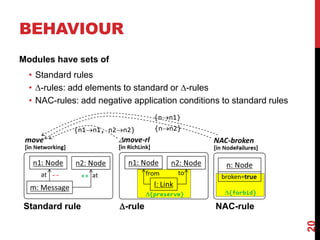
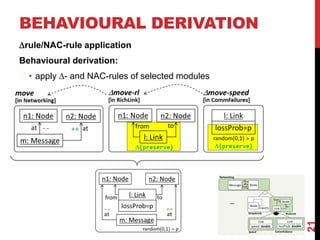
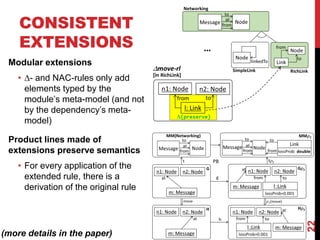
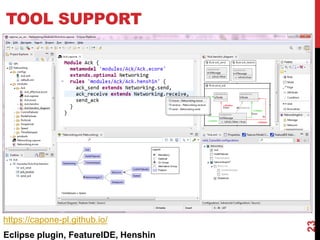
This document presents a modular approach to defining families of domain-specific languages (DSLs) using graph transformations. The approach uses language modules that define the abstract syntax and semantics of DSL variants. Module dependencies and extensions define how the variants relate and combine. Configurations select modules to derive a specific DSL meta-model and rules. The approach reduces specification effort compared to defining each variant separately while ensuring behavioral consistency. Tool support and experiments demonstrate the feasibility of the modular approach.

1. MODULAR LANGUAGE
PRODUCT LINES
A GRAPH TRANSFORMATION APPROACH
MODELS’2022, Montreal
Juan de Lara1, Esther Guerra1, Paolo Bottoni2
1Universidad Autónoma de Madrid (Spain)
2Sapienza University of Rome (Italy)

2. FROM DSLs TO
DSL FAMILIES
Modelling languages
• Essential for engineering disciplines
• Model-driven Engineering
• Domain-specific Languages (DSLs)
Does ONE language fit ALL?
• Different users: education, low-code development
Example: Class diagrams with different levels of sophistication
• Different expressivity: modelling purpose, analyses
Example: Petri nets with inhibitor, read arcs, time, colours
• Different levels of precision: to support different project phases
Example: From sketch-like diagrams to fully precise models
Language families!
2

3. EXAMPLE
A DSL FAMILY FOR NETWORKING
3
Simple link with node
failures and acks

4. 4
Simple link with node
failures and acks
Rich links with
communication failures
EXAMPLE
A DSL FAMILY FOR NETWORKING

5. 5
Simple link with node
failures and acks
Rich links with
communication failures
Rich links with
communication failures
and time
EXAMPLE
A DSL FAMILY FOR NETWORKING

6. HOW TO DEFINE A
LANGUAGE FAMILY?
Define each DSL separately (clone & own)
• Meta-models and rules share commonalities
• Adding a new feature (e.g., ad-hoc networks) doubles the
family size
Define just one “super-language” with all features
• Language difficult to use for users
• Unnecessary concepts
• What about alternative elements (rich vs. simple links)?
6

7. OUR GOAL
A technique to define and manage DSL families that is
• Succinct
(much) less effort than specifying each language variant in isolation
• Extensible
Adding a new variant should be easy, leave existing variants unchanged
Incremental language construction
• Reusable
Specifications of variants as reusable as possible to minimise effort and
avoid duplications
• Analysable
Ensure the behaviour of its variants is compatible with the base behaviour
of the language
7

8. THE APPROACH
8
...
extension roles
optional
mandatory
alternative
or
M
(dependency)
MM
rule_i
rule_i
rulei
M1
(extension)
MM1
rule_i
rule_i
rulej
Mn
(extension)
MMn
rule_i
rule_i
rulek
role of Mn in dependency
inclusion of MMn in MM
{C1→C3,...}
{C1→C2,...}
rule extension
1
2
3
1
2
3
Language product line
Language modules
• Meta-model
• Transformation rules
Module dependencies
Module extensions
• Extension roles
• As in feature models

9. LANGUAGE PRODUCT LINE
EXAMPLE
9
Meta-model elements are identified by name

10. 10
Meta-model elements are identified by name
top module
LANGUAGE PRODUCT LINE
EXAMPLE

11. 11
Meta-model elements are identified by name
top module
Cross-tree
constraints
LANGUAGE PRODUCT LINE
EXAMPLE

12. USING THE PRODUCT LINE:
CONFIGURATIONS
12
A set of modules such that
• All top modules are selected
• If a module is selected, then the configuration needs selecting:
1. all mandatory extension modules
2. exactly one alternative extension modules
3. at least one OR extension module
4. its dependency
• The cross-tree constraints evaluate to true

13. CONFIGURATIONS
EXAMPLE
13
Some configurations:

14. CONFIGURATIONS
EXAMPLE
14
Some configurations:
• {Networking, SimpleLink}

15. CONFIGURATIONS
EXAMPLE
15
Some configurations:
• {Networking, SimpleLink}
• {Networking, SimpleLink, NodeFailures, Ack}

16. CONFIGURATIONS
EXAMPLE
16
Some configurations:
• {Networking, SimpleLink}
• {Networking, SimpleLink, NodeFailures, Ack}
• {Networking, RichLink, CommFailures}

17. CONFIGURATIONS
EXAMPLE
17
Some configurations:
• {Networking, SimpleLink}
• {Networking, SimpleLink, NodeFailures, Ack}
• {Networking, RichLink, CommFailures}
• {Networking, RichLink, CommFailures, TimeStamped, Speed}

18. DERIVATION:
GETTING THE META-MODEL
Given a configuration
• Merge the meta-model fragments of all modules (co-limit)
18
1= {Networking, SimpleLink,
NodeFailures, Ack}
MM1

19. BEHAVIOUR
Modules have sets of
• Standard rules
• -rules: add elements to standard or -rules
• NAC-rules: add negative application conditions to standard rules
19
Standard rule -rule NAC-rule

20. BEHAVIOUR
Modules have sets of
• Standard rules
• -rules: add elements to standard or -rules
• NAC-rules: add negative application conditions to standard rules
20
Standard rule -rule NAC-rule
{n1→n1, n2→n2}
{n→n1}
{n→n2}

21. BEHAVIOURAL DERIVATION
rule/NAC-rule application
Behavioural derivation:
• apply - and NAC-rules of selected modules
21

22. CONSISTENT
EXTENSIONS
Product lines made of
extensions preserve semantics
• For every application of the
extended rule, there is a
derivation of the original rule
22
Modular extensions
• - and NAC-rules only add
elements typed by the
module’s meta-model (and not
by the dependency’s meta-
model)
(more details in the paper)

23. TOOL SUPPORT
23
https://capone-pl.github.io/
Eclipse plugin, FeatureIDE, Henshin

24. EXPERIMENTS
24
Effort reduction w.r.t. explicit definition of each language variant
• Reduces specification size by 86% – 96.6%
• Reduces rule size 91.7% – 97.7%
Effort of adding a new feature?
• Meta-model of sizes 3 – 4 (vs. meta-model size 12 – 22 +
replicating the existing meta-models)
• Between 1 and 2 rules of sizes 3 – 6 (vs. 3 to 12 rules with sizes
between 7 and 14)
(results for rules omitted)

25. CONCLUSIONS AND
FUTURE WORK
Modular approach to define language families
• Considers abstract syntax and semantics
Analysis, tool support, experiments
Future Work
• Fine-granular analysis of (in-)consistency
• Effective testing techniques
• Consider richer meta-model notions (e.g., OCL)
• Modules with several dependencies
• Consider concrete syntax
25

26. https://capone-pl.github.io/
THANKS!
Juan.deLara@uam.es
@miso_uam