The document summarizes key concepts about the Laplace transform. It defines the Laplace transform, discusses properties like linearity and time shifting. It provides examples of taking the Laplace transform of unit step functions. It also covers computing the inverse Laplace transform using partial fraction expansion and handling cases with repeated or complex poles.

1. Signals & Systems
Chapter 3
The Laplace Transform
INC212 Signals and Systems : 2 / 2554

2. Laplace Transform of
unit-step Function
∞
∞ X (σ + jω ) = ∫ e −(σ + jω ) t dt
X (ω ) = ∫ x(t )e − j ωt
dt 0
−∞ 1
∞
X (σ + jω ) = − [e −(σ + jω ) t ]tt =∞
=0
σ + jω
X (ω ) = ∫ 1⋅ e − jωt dt
0 1
X (σ + jω ) = − [ 0 − e − (σ + j ω ) 0 ]
σ + jω
∞
X (ω ) = ∫ e e −σt − jωt
dt X (σ + jω ) =
1
−∞
σ + jω
∞
X (ω ) = ∫ e −(σ + jω ) t dt σ + jω → s
0
1
X ( s) =
s
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

3. Laplace Transform of Signals
∞
X ( s ) = ∫ x(t )e dt ; s = σ + jω
− st
−∞
One-side transform x(t ) = 0; t < 0
∞
X ( s ) = ∫ x(t )e dt − st
0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

4. Laplace Transform of Signals
∞ 1, t ≥ 0
X ( s ) = ∫ x(t )e dt − st
x(t ) = u (t ) = 
0 0, t < 0
∞ ∞
L[u (t )] = ∫ u (t )e dt − st
= ∫ (1)e − st dt
−∞ 0
− st ∞
e 1
=− = −0 − (− ), s > 0
s 0
s
1
∴ L[u (t )] = , s > 0
s
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

5. Relationship between the FT and ℒ T
One-side transform or Forward transform
x(t ) = 0; t < 0 ∴ s = jω ; σ = 0
∞ ∞
X (ω ) = ∫ x(t )e − jω t
dt X ( s ) = ∫ x(t )e − st dt
0 0
X (ω ) = X ( s ) s = jω
x(t ) ↔ X ( s )
X ( s) = L[ x(t )] ; x(t ) = L−1[ X ( s )]
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

6. Common ℒ T Pairs
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

7. Region of Convergence (ROC)
 g1 (t ) = Aeαt u (t ); α > 0
∞ ∞ ∞
G1 ( s ) = ∫
−∞
Aeαt u (t )e − st dt = A∫ e −( s −α )t dt = A∫ e (α −σ )t e − jωt dt
0 0
A
∴ G1 ( s ) = σ = Re( s ) > α
s −α
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

8. Region of Convergence (ROC)
 g 2 (t ) = Ae −αt u (−t ) = g1 (−t ); α > 0
∞ 0 0
G2 ( s ) = ∫
−∞
Ae −αt u (−t )e − st dt = A ∫ e −( s +α )t dt = A ∫ e −(σ +α )t e − jωt dt
−∞ −∞
A
∴ G2 ( s) = = G1 (− s ) σ = Re( s ) < −α
s +α
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

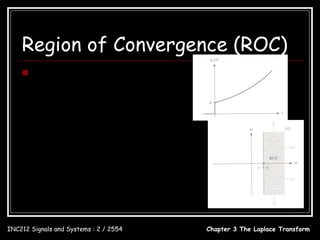
9. Region of Convergence (ROC)
 Example:
x(t ) = e − t u (t ) + e −2t u (t )
L ∞ ∞
x(t ) ↔ X ( s ) = ∫ [e u (t ) + e u (t )]e dt = A∫ [e −( s +1) t + e −( s + 2) t ]dt
−t − 2t − st
−∞ 0
1 1
∴ X (s) = + σ > −1
s +1 s + 2
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

10. Region of Convergence (ROC)
 Example:
x(t ) = e −t u (t ) + e 2t u (−t )
L1 L 1
−t
e u (t ) ↔ σ > −1 e u (−t ) ↔ −
2t
σ <2
s +1 s−2
L 1 1
−t
∴ e u (t ) + e u ( −t ) ↔
2t
− −1 < σ < 2
s +1 s − 2
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

11. Properties of the ℒT
 Linearity
L L
x(t ) ↔ X ( s ) and v(t ) ↔ V ( s )
L
ax(t ) + bv(t ) ↔ aX ( s ) + bV ( s )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

12. Properties of the ℒT
 Example: Linearity L[u (t ) + e − t u (t )]
1 −t 1
u (t ) ↔ and e u (t ) ↔
s s +1
−t 1 1
u (t ) + e u (t ) ↔ +
s s +1
−t 2s + 1
u (t ) + e u (t ) ↔
s ( s + 1)
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

13. Properties of the ℒT
 Right Shift in Time
x(t ) ↔ X ( s )
− cs
x(t − c)u (t − c) ↔ e X (s)
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

14. Properties of the ℒT
 Example: Right Shift in Time
1, 0 ≤ t < c
x(t ) = 
0, all other t
x(t ) = u (t ) − u (t − c)
− cs − cs
1 e 1− e
u (t ) − u (t − c) ↔ − =
s s s
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

15. Properties of the ℒ T
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

16. Computation of the Inverse ℒ T
1 c + j∞
2π j ∫c − j∞
x(t ) = X ( s )e st ds
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

17. The Inverse ℒ T using
Partial-Fraction Expansion
B( s)
X ( s) =
A( s )
Let p1, p2, …, pN
B ( s ) = bM s M + bM −1s M −1 +  + b1s + b0 denote the roots
A( s ) = a N s N + a N −1s N −1 +  + a1s + a0 of the equation
A( s ) = 0
The pi for i = 1, 2,
A( s ) = a N ( s − p1 )( s − p2 )  ( s − p N )
…,N are called the B( s)
X (s) =
poles of X(s) a N ( s − p1 )( s − p2 )  ( s − p N )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

18. Distinct Poles
c1 c2 cN
X ( s) = + ++
s − p1 s − p2 s − pN
ci = [( s − pi ) X ( s )]s = pi , i = 1,2, , N
x(t ) = c1e p1t
+ c2 e p2t
+  + cN e pN t
, t≥0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

19. Example: Distinct Poles
s+2 ci = [( s − pi ) X ( s )]s = pi , i = 1,2, , N
X ( s) = 3
s + 4 s 2 + 3s s+2 2
A( s ) = s + 4 s + 3s = s ( s + 1)( s + 3) c1 = [ sX ( s )]s =0 = ( s + 1)( s + 3)
3 2 =
3
s =0
A( s ) = 0 = s ( s + 1)( s + 3)
s+2 1
p1 = 0, p2 = −1, p3 = −3 c2 = [( s + 1) X ( s )]s = −1 = =
s ( s + 3) s = −1 − 2
c1 c2 c3
X ( s) = + + s+2 −1
s − 0 s − (−1) s − (−3) c3 = [( s + 3) X ( s )]s = −3 = =
s ( s + 1) s = −3 6
c c c
X ( s) = 1 + 2 + 3 2 1 − t 1 − 3t
s s +1 s + 3 x(t ) = − e − e , t ≥ 0
3 2 6
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

20. Distinct Poles with 2 or More
Poles Complex
c1 c1 c3 cN
X (s) = + + ++
s − p1 s − p1 s − p3 s − pN
x(t ) = c1e p1t
+ c1e p1t
+ c3e p3t +  + c N e p N t
σt
c1e p1t
+ c1e p1t
= 2 c1 e cos(ωt + ∠c1 )
σt
x(t ) = 2 c1 e cos(ωt + ∠c1 ) + c3e p3 t
+  + cN e pN t
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

21. Example: Distinct Poles with 2 or
More Poles Complex
ci = [( s − pi ) X ( s)]s = p , i = 1,2,, N
s − 2s + 1
2 i
X (s) = 3 s 2 − 2s + 1
s + 3s 2 + 4 s + 2 c1 = [( s + 1 − j ) X ( s )]s =−1+ j =
( s + 1 + j )( s + 1) s =−1+ j
A( s ) = s 3 + 3s 2 + 4 s + 2
= ( s + 1 − j )( s + 1 + j )( s + 1) −3
c1 = + j2
2
p1 = −1 + j , p2 = −1 − j , p3 = −1
9 5
c1 = +4 = ;
X ( s) =
c1
+
c1
+
c3 4 2
s − (−1 + j ) s − (−1 − j ) s − (−1) −4
∠c1 = 180° + tan −1 = 126.87°
c1 c1 c3 3
X ( s) = + +
s +1− j s +1+ j s +1 s 2 − 2s + 1
c3 = [( s + 1) X ( s )]s = −1 = 2 =4
s + 2 s + 2 s = −1
x(t ) = 5e −t cos(t + 126.87°) + 4e − t , t ≥ 0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

22. Repeated Poles
B( s) c c2 cr c cN
X (s) = X ( s) = 1 + ++ + r +1 +  +
A( s ) s − p1 ( s − p1 ) 2 ( s − p1 ) r s − pr +1 s − pN
ci = [( s − pi ) X ( s )]s = pi , i = r + 1, r + 2, , N
cr = [( s − p1 ) r X ( s )]s = p1
1d 
i = 1,2,  , r − 1 i = 1; cr −1 = [( s − p1 ) r X ( s )]
1!  ds
  s = p1
1  di 
cr − i =  i [( s − p1 ) X ( s )]
r
1  d2 
i!  ds  s = p1 i = 2; cr − 2 =  2 [( s − p1 ) r X ( s )]
2!  ds  s= p 1
x(t ) = c1e p1t + c2te p1t +  + cr t r −1e p1t + cr +1e pr +1t +  + c N e p N t , t ≥ 0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

23. Example: Repeated Poles
5s − 1 c1 c2 c
X (s) = 3 X (s) = + + 3
s − 3s − 2 s + 1 ( s + 1) 2 s − 2
1d   d 5s − 1  −9
c1 = [( s + 1) 2 X ( s )] = [ ] = = −1
1!  ds
  s = −1  ds s − 2  s = −1 ( s − 2)
2
s = −1
5s − 1
c2 = [( s + 1) 2 X ( s )]s = −1 = =2
s − 2 s = −1
5s − 1
c3 = [( s − 2) X ( s )]s = 2 = =1
( s + 1) 2 s =2
x(t ) = −e − t + 2te − t + e 2t , t ≥ 0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

24. Case when M ≥ N
B(s)
X (s) =
A( s ) R( s)
X ( s) = Q( s) +
B( s ) = bM s M + bM −1s M −1 +  + b1s + b0 A( s )
A( s ) = a N s N + a N −1s N −1 +  + a1s + a0
R( s)
X ( s ) = Q( s ) + V ( s ), V ( s ) =
A( s )
Q(s)
A( s ) B( s ) x(t ) = q (t ) + v(t )
A( s ) * Q ( s ) dN
q(t ); δ (t ) ↔ s N
R( s) dt N
v(t ); v(t ) ↔ V ( s )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

25. Example: Case when M ≥ N
s 3 + 2s − 4 20 s − 12
X (s) = 2 = s−4+ 2
s + 4s − 2 s + 4s − 2
X ( s) = Q( s) + V ( s)
Q( s) = s − 4
d
q(t ) = δ (t ) − 4δ (t )
dt
20s − 12 20.6145 0.6145
V ( s) = 2 = −
s + 4 s − 2 s + 4.4495 s − 0.4495
v(t ) = 20.6145e − 4.4495t − 0.6145e 0.4495t , t ≥ 0
d
x(t ) = δ (t ) − 4δ (t ) + 20.6145e − 4.4495t − 0.6145e 0.4495t , t ≥ 0
dt
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

26. Transform of the I/O
Differential Equation
 First-Order Case
y (0 − ) b
Y ( s) = + X (s)
dy (t ) s+a s+a
+ ay (t ) = bx(t ) b
dt Y ( s) = X (s)
sY ( s ) − y (0 − ) + aY ( s ) = bX ( s ) s+a
b
( s + a )Y ( s ) = y (0 − ) + bX ( s ) H (s) =
s+a
Y ( s) = H ( s) X ( s)
H(s) Transfer Function (TF) of the system
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

27. Transform of the I/O
Differential Equation
 Example: First-Order Case
dy (t ) 1 1
+ y (t ) = x(t )
dt RC RC
y (0 − ) 1 RC
Y ( s) = +
s + 1 RC ( s + 1 RC ) s
y (0 − ) 1 RC
Y (s) = + X (s) y (0 − ) 1 1 RC
s + 1 RC s + 1 RC Y ( s) = + −
s + 1 RC s s + 1 RC
y (t ) = y (0 − )e −(1 RC ) t + 1 − e −(1 RC ) t , t ≥ 0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

28. Transform of the I/O
Differential Equation
 Second-Order Case
d 2 y (t ) dy (t ) dx(t )
2
+ a1 + a0 y (t ) = b1 + b0 x(t )
dt dt dt
[ ]
s 2Y ( s ) − y (0 − ) s − y (0 − ) + a1 sY ( s ) − y (0 − ) + a0Y ( s ) = b1sX ( s ) + b0 X ( s )

y (0 − ) s + y (0 − ) + a1 y (0 − )
 b1s + b0
Y (s) = + 2 X ( s)
s + a1s + a0
2
s + a1s + a0
If initial condition = 0 :
b1s + b0 b1s + b0
Y (s) = 2 X ( s) ; H ( s) = 2
s + a1s + a0 s + a1s + a0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

29. Transform of the I/O
Differential Equation
 Example: Second-Order Case
x(t) = u(t) so that X(s) = 1/s; initial cond. = 0
d 2 y (t ) dy (t )
2
+6 + 8 y (t ) = 2 x(t )
dt dt
2
H (s) = 2 2 1
s + 6s + 8 Y (s) = H (s) X (s) =
s 2 + 6s + 8 s
0.25 0.5 0.25
Y (s) = − +
s s+2 s+4
y (t ) = 0.25 − 0.5e − 2t + 0.25e − 4t , t ≥ 0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

30. Transform of the I/O
Differential Equation
 Example: Second-Order Case y (0 − ) = 1
x(t) = u(t) with the initial condition
y (0 − ) = 2

s +8 2 1
Y ( s) = 2 + 2
s + 6s + 8 s + 6s + 8 s
s 2 + 8s + 2
=
s ( s 2 + 6 s + 8)
0.25 2.5 1.75
Y ( s) = + −
s s+2 s+4
y (t ) = 0.25 + 2.5e − 2t − 1.75e − 4t , t ≥ 0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

31. Transform of the I/O
Differential Equation
 Nth-Order Case
d N y (t ) N −1 d i y (t ) M d i x(t ) C (s) B(s)
N
+ ∑ ai i
= ∑ bi i
; Y ( s) = + X (s)
dt i =0 dt i =0 dt A( s ) A( s )
B ( s ) = bM s M + bM −1s M −1 +  + b1s + b0 ; A( s ) = s N + a N −1s N −1 +  + a1s + a0
C ( s ) = y ( 0 − ) s + y ( 0 − ) + a1 y ( 0 − )

B( s) bM s M +  + b1s + b0
Y (s) = X (s) = N N −1
X (s)
A( s ) s + a N −1s +  + a1s + a0
bM s M +  + b1s + b0
H (s) = N
s + a N −1s N −1 +  + a1s + a0
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

32. Transform of the I/O
Convolution Integral
t
y (t ) = h(t ) ∗ x(t ) = ∫ h(λ ) x(t − λ )dλ , t ≥ 0
0
Y ( s) = H ( s) X ( s)
h(t ) ↔ H ( s )
Y (s)
H (s) =
X (s)
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

33. Transform of the I/O
Convolution Integral
 Example: Determining the TF
y (t ) = 2 − 3e −t + e −2t cos 2t , t ≥ 0 2 3 s+2
− +
2 3 s+2 s s + 1 ( s + 2) 2 + 4
Y (s) = − + H (s) =
s s + 1 ( s + 2) + 4 2 1
s +1
1 2( s + 1) ( s + 1)( s + 2)
X (s) = = −3+
s +1 s ( s + 2) 2 + 4
[2( s + 1) − 3s ][( s + 2) 2 + 4] + s ( s + 1)( s + 2)
=
s[( s + 2) 2 + 4]
s 2 + 2s + 16
= 3
s + 4 s 2 + 8s
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

34. Transform of the I/O
Convolution Integral
 Finite-Dimensional Systems
bM s M + bM −1s M −1 +  + b1s + b0
H ( s) = N
s + a N −1s N −1 +  + a1s + a0
( s N + a N −1s N −1 +  + a1s + a0 )Y ( s ) = (bM s M + bM −1s M −1 +  + b1s + b0 ) X ( s )
d N y (t ) N −1 d i y (t ) M d i x(t )
N
+ ∑ ai i
= ∑ bi
dt i =0 dt i =0 dt i
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

35. Transform of the I/O
Convolution Integral
 Poles and zeros of a Systems
bM s M + bM −1s M −1 +  + b1s + b0
H ( s) = N
s + a N −1s N −1 +  + a1s + a0
bM ( s − z1 )( s − z 2 )  ( s − z M )
H ( s) =
( s − p1 )( s − p2 )  ( s − p N )
zi : “zeros of H (s)” or “zeros of system”
pi : “poles of H (s)” or “poles of system”
N : “number of poles of system” or “order N of system”
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

36. Transform of the I/O
Convolution Integral
 Example: Third-Order System
2 s 2 + 12 s + 20
H ( s) = 3
s + 6 s 2 + 10s + 8
2( s + 3 − j )( s + 3 + j )
H ( s) =
( s + 4)( s + 1 − j )( s + 1 + j )
z1 = −3 + j and z1 = −3 − j
p1 = −4, p 2 = −1 + j , p3 = −1 − j
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

37. Exercises
 Sketch the pole-zero plot and ROC for
these signals.
 x(t ) = e −8t u (t )
 x(t ) = e 3t cos(20πt )u (−t )
 x(t ) = e 2t u (−t ) − e −5t u (t )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

38. Exercises
 Using the time-shifting property, find
the LT of these signals.
 x(t ) = u (t ) − u (t − 1)
 x(t ) = 3e −3(t − 2)u (t − 2)
 x(t ) = 3e −3t u (t − 2)
 x(t ) = 5 sin(π (t − 1))u (t − 1)
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

39. Exercises
 Find the inverse LT of these functions.
 24  20
X ( s) = X (s) =
s ( s + 8) s 2 + 4s + 3
 s2  s
X ( s) = 2 X ( s) = 2
s − 4s + 4 s + 4s + 4
 5  2s
X ( s) = 2 X ( s) = 2
s + 6 s + 73 s + 2 s + 13
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

40. INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

41. Direct Construction of the TF
 RLC Circuits
dv(t ) 1
= i (t )
dt C
v(t ) = Ri (t ) di (t )
1 v(t ) = L
sV ( s ) − v(0) = I ( s ) dt
V ( s ) = RI ( s ) C
1 1 V ( s ) = LsI ( s ) − Li (0)
V (s) = I ( s ) + v(0)
Cs s
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

42. Direct Construction of the TF
 Series and Parallel Connection
Z1 ( s ) Z 2 (s)
V1 ( s ) = V ( s) I1 ( s ) = I ( s)
Z1 ( s ) + Z 2 ( s ) Z1 ( s ) + Z 2 ( s )
Z 2 (s) Z1 ( s )
V2 ( s ) = V ( s) I 2 (s) = I ( s)
Z1 ( s ) + Z 2 ( s ) Z1 ( s ) + Z 2 ( s )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

43. Direct Construction of the TF
 Example: Series RLC Circuit
Output = VC(s) Output = VR(s)
1 Cs R
Vc ( s ) = X ( s) VR ( s ) = X (s)
Ls + R + (1 Cs ) Ls + R + (1 Cs )
1 LC ( R L) s
= 2 X ( s) = 2 X ( s)
s + ( R L) s + (1 LC ) s + ( R L) s + (1 LC )
1 LC ( R L) s
H ( s) = 2 H ( s) = 2
s + ( R L) s + (1 LC ) s + ( R L) s + (1 LC )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

44. Direct Construction of the TF
 Interconnections of Integrators
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

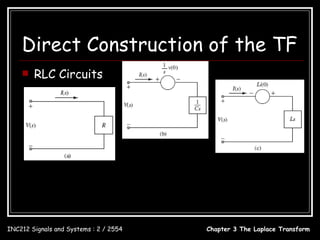
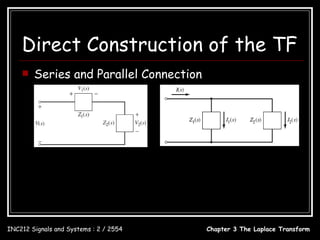
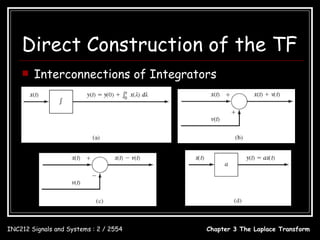
45. Direct Construction of the TF
sQ1 ( s) = −4Q1 ( s ) + X ( s)
 Example: Q1 ( s) =
1
s+4
X (s)
sQ2 ( s ) = Q1 ( s) − 3Q2 ( s) + X ( s )
1
Q2 ( s ) = [Q1 ( s ) + X ( s )]
s+3
1  1 
=  + 1 X ( s )
s +3 s +4 
s+5
= X ( s)
( s + 3)( s + 4)
Y ( s ) = Q2 ( s ) + X ( s )
s+5
= X ( s) + X ( s)
( s + 3)( s + 4)
s 2 + 8s + 17
= X ( s)
( s + 3)( s + 4)
s 2 + 8s + 17 s 2 + 8s + 17
H ( s) = =
( s + 3)( s + 4) s 2 + 7 s + 12
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

46. TF of Block Diagrams
 Parallel Interconnection
Y ( s ) = Y1 ( s ) + Y2 ( s )
Y1 ( s ) = H1 ( s ) X ( s )
Y2 ( s ) = H 2 ( s ) X ( s )
Y ( s ) = H1 ( s ) X ( s ) + H 2 ( s) X ( s)
= ( H1 ( s ) + H 2 ( s )) X ( s )
H ( s) = H1 ( s) + H 2 ( s )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

47. TF of Block Diagrams
 Series Connection
Y1 ( s ) = H1 ( s ) X ( s )
Y2 ( s ) = H 2 ( s )Y1 ( s )
Y ( s ) = Y2 ( s ) = H 2 ( s ) H1 ( s ) X ( s )
H ( s ) = H 2 ( s ) H1 ( s ) = H1 ( s ) H 2 ( s )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

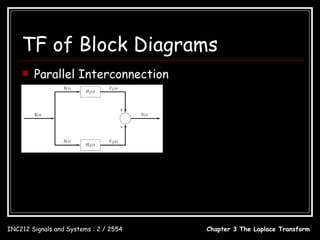
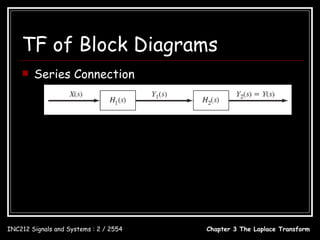
48. TF of Block Diagrams
 Feedback Connection Y ( s) = H1 ( s) X 1 ( s)
X 1 ( s ) = X ( s ) − Y2 ( s )
= X ( s ) − H 2 ( s )Y ( s )
Y ( s ) = H1 ( s )[ X ( s ) − H 2 ( s )Y ( s )]
H1 ( s )
Y (s) = X (s)
1 + H1 ( s) H 2 ( s)
H1 ( s)
H (s) =
1 + H1 ( s) H 2 ( s)
H1 ( s)
H (s) =
1 − H1 ( s ) H 2 ( s )
INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform

49. INC212 Signals and Systems : 2 / 2554 Chapter 3 The Laplace Transform