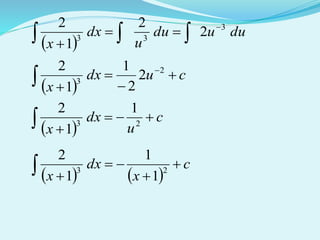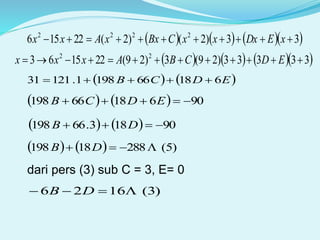Dokumen ini membahas berbagai teknik pengintegralan dalam kalkulus, termasuk substitusi dan rumus integral fungsi trigonometri, logaritma, dan eksponen. Contoh-contoh disertakan untuk menggambarkan penerapan teknik-teknik ini dalam mencari anti turunan. Selain itu, dokumen ini memberikan latihan untuk menguji pemahaman pembaca tentang konsep yang dijelaskan.

1. oleh
Bahan Ajar Kalkulus II
Teknik-Teknik Pengintegralan
(disarikan dari buku Purcell, edisi 8)
Muh Hendra S Ginting
Depertemen Teknik Kimia
Fakultas Teknik USU
Medan 2015

2. Definisi
adalah suatu metode/teknik dalam
penyelesaian mencari anti turunan/integrasi
1.Pengintegralan dengan substitusi
Teorima A
untuk menentukan ∫ f(x) dx , kita dapat
mensubtitusi u = g (x) dengan g fungsi yang
dapat diintegralkan. Apabila subtitusi itu
mengubah f (x) dx menjadi h(u) du dan
apabila H sebuah anti turunan h, maka
Teknik-Teknik Pengintegralan

3.    cugHcuHduuhdxxf   )()()(
biasanya digunakan subtitusi fungsi
konstanta, fungsi pangkat, eksponen, fungsi
trigonometri, dan fungsi invers trigonometri
a.Substitusi konstanta, pangkat
c
n
x
dxx
n
n




 1
.1
1
dxxfkdxxfk   )()(.2

4. Contoh 1
Hitunglah
Penyelesaian
  dxxx 143
misalkan 14
 xu
)1( 4
 xddu
dxxdu 3
4
3
4x
du
dx maka
3
2
1
343
4
1
x
du
uxdxxx  
gunakan aturan konstanta

5. duudxxx   2
1
43
4
1
1
cudxxx 




1
2
1
43
1
2
1
1
4
1
1
cudxxx  2
3
43
3
2
4
1
1
  cxcudxxx  2
3
42
3
43
1
6
1
6
1
1
gunakan aturan pangkat

6. b. Substitusi trigonometri
cxdxx  cossin.1
cxdxx  sincos.2
cxdxx  coslntan.3
cxdxx  tansec.4 2
canxdxxec  cotcos.5 2
cxdxxx  sectansec.6
cecxdxanxecx  coscotcos.7

7. Contoh 2
Hitunglah
Penyelesaian
 dx
x
x
)(cos 22
misalkan 2
xu 
)( 2
xddu 
dxxdu 2
x
du
dx
2
maka
gunakan subs trigonometri
x
du
u
x
dx
x
x
2cos)(cos 222  

8. 2cos
1
)(cos 222
du
u
dx
x
x
 
u
u
2
2
sec
cos
1
catatan
maka
cudx
x
x
 tan
2
1
)(cos 22
  udu
du
u
dx
x
x 2
222
sec
2
1
2cos
1
)(cos
cxdx
x
x
 )(tan
2
1
)(cos
2
22

9. c. Substitusi fungsi invers (balikan) trigonometri
jika yx tan dyydx 2
sec
ydx
dy
2
sec
1

perhatikan segi tiga berikut
y
x
1
12
x
yx tan
1
1
cos
2


x
y
1
1
cos 2
2


x
y
1sec 22
 xy
y
dx
dy 2
sec

ydx
dy
2
sec
1

12


x
dx
dy

10. 12


x
dx
dy
12

  x
dx
dy
12

  x
dx
y
jika yx tan xxarcy 1
tantan 

maka cxarc
x
dx

 tan
12
jika c
a
x
arc
aax
dx







 tan
1
22
dimana a, c adalah konstanta

11. Berikut ini dirangkumkan beberapa rumus
integral substitusi fungsi invers (balikan)
trigonometri
 








c
a
x
xa
dx 1
22
sin.1
c
x
a
a
c
a
x
aaxx
dx






















11
22
cos
1
sec
1
.2
c
a
x
aax
dx










1
22
tan
1
.3

12. Contoh 3
Hitunglah
Penyelesaian
 
dx
xx 256
7
2
 

 1696
7
256
7
22
xx
dx
dx
xx
 

 16)96(
7
256
7
22
xx
dx
dx
xx
 

 16)3(
7
256
7
22
x
dx
dx
xx

13. ingat
3 xumisalkan dxdu 
 

 16)3(
7
256
7
22
x
dx
dx
xx
 

 222
4
7
256
7
u
du
dx
xx
c
a
x
aax
dx










1
22
tan
1
Maka, a = 4
c
a
u
u
du
dx
xx












1
222
tan
4
1
.7
4
7
256
7

14. c
x
dx
xx





 



 4
)3(
tan
4
7
256
7 1
2
Contoh 4
Hitunglah  
dx
x2
95
3
Penyelesaian
misalkan xu 3 22
9xu 
)3( xddu 
3
du
dx 
dxdu 3

15. maka
 




du
u
dx
x 222
5
1
3
95
3
ingat  








c
a
x
xa
dx 1
22
sin
  

 35
1
3
95
3
222
du
u
dx
x
 2
55 

16. c
x
dx
x









 5
3
sin
95
3 1
2
 
c
u
du
u
dx
x











 5
sin
5
1
95
3 1
222
d. Substitusi eksponen
cedxe xx


17. Contoh 5
Hitunglah
penyelesaian
 dx
x
e x
2
/1
6
misalkan
x
u
1

dx
xx
ddu 2
1
)
1
( 
duxdx 2
maka
gunakan subs eksponen
 dux
x
e
dx
x
e ux
2
22
/1
6
6
 
cedxe xx


18. cecedx
x
e xu
x

/1
2
/1
66
6
maka cedue uu

duedx
x
e u
x
  6
6
2
/1

19. Latihan 1
Hitunglah
dxx  5
)2(.1
  4
.2 2
x
dx
dx
x
x
  4
.3 2
dxxe x
sin..4 cos

dx
x
x
 
4/
0
2
sin1
cos
.5


20. e. Substitusi fungsi logaritma asli (natural)
cxdx
x
 ln
1
0x
Jika x menggantikan u
cudu
u
 ln
1
0u

21. Contoh 6
Hitunglah dx
x  72
5
penyelesaian
misalkan 72  xu
)72(  xddu
dxdu 2
2
1
5
72
5 du
u
dx
x  

2
du
dx 
maka

22. cu
u
du
dx
x

  ln
2
5
2
5
72
5
  cxdx
x

 72ln
2
5
72
5
Sifat-sifat logaritma asli
01ln.1 
ba
b
a
lnlnln.2 
baba lnln.ln.3 
axax
ln.ln.4 

23. Latihan 2
Hitunglah
dx
x 12
1
.1
dx
x  21
1
.2
 
dx
xx

2
ln.
1
.3

24. f. Fungsi eksponensial berbasis a
Tinjau aturan diferensial fungsi eksponensial
x
ay 
axay x
ln.lnln 
)ln.()(ln axdyd 
dxa
y
dy
.ln
yayD
dx
dy
x .ln x
x aayD
dx
dy
.ln

25. maka
ca
a
dxa xx






 ln
1
sehingga
1a
x
aa
dx
dy
.ln dxaady x
.ln
dxa
a
dy x

ln
a
dy
dxax
ln 

26. Contoh 7
Hitunglah dxxx

2
.2
3
penyelesaian
misalkan
3
xu 
dxxdu 2
3
2
3x
du
dx maka
)( 3
xddu 
  2
22
3
2.2
3
x
du
xdxx ux

27.   2
22
3
2.2
3
x
du
xdxx ux
  dudxx ux
2
3
1
.2 23
cdxx
x
x
 2ln.3
2
.2
3
3
2

28. Contoh 8
Hitunglah dx
x
x

1
2/1
2
/1
5
penyelesaian
misalkan
x
u
1

maka
dx
x
du 2
1

 
1
2/1
2
2
1
2/1
2
/1
.
55
dux
x
dx
x
ux
dxxdu  2
.
1
2/1
/11
2/1
1
2/1
2
/1
5ln
5
5ln
5
5
5 

 
x
x
xu
u
x
dudx
x
  )5(5
5ln
1
5ln
55 2/11
1
2/1
1
2/1
2
/1




x
x
xx
dx
x

29. Latihan 3
Hitunglah


dxx 15
10.1
dx
x
x

4
1
5
.2

30. 2. Integral Subtitusi Trigonometri
Bila kita mengkombinasikan metode dengan
pemakaian kesamaan trigonometri yang tepat,
maka kita dapat mengintegralkan banyak
bentuk trigonometri, maka integral yang
sering muncul adalah :
dxxdandxx nn
 cossin.1
dxxx nn
cos.sin.2 
dxnxxm cos.sin.3  dxnxxm sin.sin
dxnxxm cos.cos

31. Jenis 1  dxxdxx nn
 cos,sin
tinjaulah kasus apabila n bilangan bulat
positip dan ganjil, keluarkan faktor sin x atau
cos x.
gunakan kesamaan 1cossin 22
 xx
Soal no 3 hal 388
Hitunglah dxx
3
sin
penyelesaian
dxxxdxx sin.sinsin 23
 
keluarkan faktor sin x

32. 1cossin 22
 xxgunakan aturan
xx 22
cos1sin 
  dxxxdxx sincos1sin 23
 
   xdxdxx coscos1sin 23
 
      xdxxddxx cos.coscossin 23
cxxxdx 
33
cos
3
1
cossin

33. Contoh 9
Hitunglah dxx
5
sin
penyelesaian
dxxxdxx sin.sinsin 45
 
keluarkan faktor sin x
gunakan aturan 1cossin 22
 xx
xx 22
cos1sin 

34.   dxxxdxx sincos1sin
2
25
 
  dxxxxdxx sincoscos21sin 425
 
   xdxxdxx coscoscos21sin 425
 
     xdxxdxxddxx cos.coscos.cos2cossin 425
  
cxxxxdx 
535
cos
5
1
cos
3
2
cossin

35. Contoh 10
carilah dxx
2
sin
penyelesaian
gunakan kesamaan setengah sudut
  xxx
xxx
22
22
sinsin12cos
sincos2cos


2
2cos1
sin2 x
x


  dx
x
dxx 


2
2cos1
sin2
dxxdxdxx    2cos
2
1
2
1
sin2

36. dxxdxdxx    2cos
2
1
2
1
sin2
 xdxdxdxx 22cos
4
1
2
1
sin2
  
cxxdxx  2sin
4
1
2
1
sin2
Contoh 11
carilah dxx
4
cos

37. penyelesaian
  1cos2cos1cos2cos
sincos2cos
222
22


xxxx
xxx
2
2cos1
cos2 x
x


 




 
 dx
x
dxx
2
4
2
2cos1
cos
   dxxxdxx 2cos2cos21
4
1
cos 24
   dxxdxxdxdxx 2cos
4
1
2cos
2
1
4
1
cos 24

38.       dxxxdxdxdxx 4cos1
2
1
4
1
22cos
2
1
2
1
4
1
cos4
2
4cos1
2cos2 x
x

ingat
      xdxdxxdxdxdxx 44cos
4
1
8
1
8
1
22cos
4
1
4
1
cos4
      xdxxdxdxdxx 44cos
32
1
22cos
4
1
8
3
cos4
cxxxdxx  4sin
32
1
2sin
4
1
8
3
cos4

39. Jenis 2 xdxx nm
cossin
jika salah satu m atau n bilangan bulat
positip ganjil sedangkan eksponen yang
satunya bilangan sembarang, kita faktorkan
kesamaan 1cossin 22
 xx
Contoh 12
xdxx 43
cossin 
m atau n ganjil carilah
penyelesaian
xdxxxxdxx 4243
cossin.sincossin 
 
xxxx 2222
cos1sin1cossin 

40. dxxxdxx 4243
cossin.sincossin 
 
  dxxxxdxx sincos.cos1cossin 4243 
 
  dxxxxdxx sin.coscoscossin 2443



   xdxxdxx coscoscoscossin 2443



cxxdxx 






 

121443
cos
12
1
cos
14
1
cossin
cxxdxx  

1343
coscos
3
1
cossin
cxxdxx 
 secsec
3
1
cossin 343

41. jika m atau n bilangan bulat positip genap
maka kita menggunakan kesamaan
setengah sudut untuk memperkecil derajat
imigran
Contoh 13
m atau n keduanya genap carilah dxxx 42
cossin
penyelesaian
 
2
222
2
2cos1
cos
2
2cos1
cos 




 





 

x
x
x
x
2
2cos1
sin2 x
x


2
4
2
2cos1
cos 




 

x
x

42. dx
xx
dxx
2
42
2
2cos1
2
2cos1
cossin 




 





 
 
  dxxxxdxx   2cos2cos212cos1
8
1
cossin 242
  
xxx
xxxxx
2cos2cos22cos
2cos2cos212cos2cos212cos1
32
22


   xxxxxx 2cos2cos2cos12cos2cos212cos1 322

 dxxxxdxx   2cos2cos2cos1
8
1
cossin 3242

43. 




 

2
4cos1
2cos2 x
x
  dxxxxdxx  





 2cos4cos1
2
1
2cos1
8
1
cossin 342
  dxxxxxdxx  





 2cos2cos4cos1
2
1
2cos1
8
1
cossin 242
    dxxxxxdxx  





 2cos2sin14cos1
2
1
2cos1
8
1
cossin 242
    dxxxxxxdxx  





 2sin.2cos2cos4cos1
2
1
2cos1
8
1
cossin 242
dxxxxxxdxx  





 2sin.2cos2cos4cos
2
1
2
1
2cos1
8
1
cossin 242

44. dxxxxxxdxx  





 2sin.2cos2cos4cos
2
1
2
1
2cos1
8
1
cossin 242
dxxxxdxx  





 2sin.2cos4cos
2
1
2
1
8
1
cossin 242
   



    xdxxxdxdxx 2sin2sin
2
1
44cos
8
1
2
1
8
1
cossin 242
cxxxdxx 



 2sin
6
1
4sin
8
1
2
1
8
1
cossin 342

45. Jenis 3 dxnxxm cossin dxnxxm sinsin
dxnxxm coscos
integral jenis ini muncul dalam teori arus
bolak-balik, masalah perpindahan panas,
dan masalah terapan lainnya. Untuk
menangani integral-integral ini kita gunakan
kesamaan hasil kali
    nmxnmnxmx  sinsin
2
1
cos.sin.1
    nmxnmnxmx  coscos
2
1
sin.sin.2
    nmxnmnxmx  coscos
2
1
cos.cos.3

46. Contoh 14
carilah dxxx 3cos2sin
penyelesaian
terapkan rumus no 1
    nmxnmnxmx  sinsin
2
1
cos.sin.1
dxxx 3cos2sin 3,2  nm
      dxxxdxxx 32sin32sin
2
1
3cos2sin
    dxxxdxxx sin5sin
2
1
3cos2sin

47.    dxxdxxdxxx sin
2
1
5sin
2
1
3cos2sin
    dxxxdxdxxx sin
2
1
55sin
5
1
2
1
3cos2sin
cxxdxxx  cos
2
1
5cos
10
1
3cos2sin
Contoh 15
jika m dan n bilangan bulat positip,
perlihatkan









mnjika
mnjika
dxnxxm



0
sinsin

48. jika m≠n
  





dxxnmxnmdxnxxm )(cos)(cos
2
1
sinsin
     xnmdxnm
nm
xnmdxnm
nm
dxnxxm 



    






)(cos
)(
1
2
1
)(cos
)(
1
2
1
sinsin

















x
x
xnm
nm
xnm
nm
dxnxxm )(sin
)(
1
)(sin
)(
1
2
1
sinsin
terapkan rumus no 2
    nmxnmnxmx  coscos
2
1
sin.sin
penyelesaian

49.    

























)(sin
)(
1
)(sin
)(
1
2
1
)(sin
)(
1
)(sin
)(
1
2
1
sinsin
nm
nm
nm
nm
nm
nm
nm
nm
dxnxxm
   


















)(sin
)(
1
2
1
)(sin
)(
1
2
1
)(sin
)(
1
2
1
)(sin
)(
1
2
1
sinsin
nm
nm
nm
nm
nm
nm
nm
nm
dxnxxm
0sinsin 
dxnxxm



50. jika m = n
  





dxxnmxnmdxnxxm )(cos)(cos
2
1
sinsin
  





dxxmdxnxxm 0cos)2(cos
2
1
sinsin
  





dxxmdxnxxm 1)2(cos
2
1
sinsin
   







dxdxxmdxnxxm
2
1
)2(cos
2
1
sinsin

51.     







dxmxdxm
m
dxnxxm
2
1
2)2(cos
2
1
2
1
sinsin













x
x
xxm
m
dxnxxm
2
1
)2sin(
4
1
sinsin




dxnxxm sinsin

52. Latihan 4
Hitunglah
 dxx6sin.1 4
 x3
cos.2

53. 3. Subtitusi yang merasionalkan
Integral yang melibatkan  n bax jika  n bax
muncul dalam suatu integral subtitusi  n baxu 
akan menghilangkan akar
Contoh 16
carilah   xx
dx
penyelesaian
misalkan xu  xu 2
  dxud 2
dxudu 2

54. ?
 xx
dx
 
du
uu
u
uu
udu
xx
dx
 



 1
2
2
2
 
 
 1ln2
1
1
2 



  u
u
ud
xx
dx
  cx
xx
dx

 1ln2

55. Contoh 17
carilah   dxxx 3 4.
penyelesaian
misalkan  3 4 xu
 43
 xu
 43
 xddu dxduu 2
3
     duuuudxxx 233 3.44.
43
 ux
     duuudxxx 363 434.

56.   cuudxxx 
473 3
7
3
4.
      cxxdxxx 
3/43/73 434
7
3
4.
Contoh 18
carilah   dxxx 5 2
1.
penyelesaian   5/1
1 xu
 15
 xu 15
 ux
 15
 xddu dxduu 4
5
  5/22
1 xu

57.     duuuudxxx 4255 2
5.11.  
    duuudxxx   6115 2
51.
  cuudxxx 
7125 2
7
5
12
5
1.
      cxxdxxx 
5/75/125 2
1
7
5
1
12
5
1.

58. Soal no 3 hal 393
?
43

 t
tdt
penyelesaian
43  tu 432
 tu
3
42


u
t
   432
 tdud
dtudu 32 
3
2udu
dt 

59. 





 

 u
uduu
t
tdt 3
2
3
4
43
2
  




 


duu
duu
t
tdt
82
9
1
3
2
3
4
43
2
2
cuu
t
tdt

 9
8
27
2
43
3
43  tu   2/33
43  tu
    ctt
t
tdt

 43
9
8
43
27
2
43
2/3

60. Integral yang melibatkan ;22
xa  ;22
xa  22
ax 
untuk merasionalkan tiga persamaan ini kita
membuat subtitusi trigonometri berikut
subtitusiakar pembatasan pada t
22
.1 xa  tax sin 2/2/   t
22
.2 xa  tax tan 2/2/   t
22
.3 ax  tax sec 2/,0   tt
penyederhanaan yang dicapai oleh subtitusi
ini adalah

61.   tatataaxa 222222222
cossin1sin.1 
taxa cos.1 22

  tatataaxa 222222222
sectan1tan.2 
taxa sec.2 22

  tataataax 222222222
tan1secsec.3 
taax tan.3 22


62. Contoh 19
carilah dxxa 22

penyelesaian
gunakan subtitusi tax sin 2/2/   t
  dttataddx cossin 
taxa cos22

sehingga
  dttatadxxa cos..cos22

63.   dttatadxxa cos..cos22
dttadxxa 2222
cos 
ingat 




 

2
2cos1
cos2 t
t
 dtt
a
dxxa 2cos1
2
2
22
 
ctt
a
dxxa 





 2sin
2
1
2
2
22

64.   cttt
a
dxxa  cos.sin
2
2
22
tax sin 2/2/   tpada selang
tax sin t
a
x
sin
t
x
22
xa 
a
tax sin
sehingga fungsi balikan
t
a
x
sin 











 
a
x
a
x
t 1
sinarcsin

65. dari segi tiga siku-siku
?cos t












 
a
x
a
x
t 1
sinarcsin
22
22
2
2
1 1
1sincoscos xa
aa
xa
a
x
a
x
t 













 
maka
cxa
aa
x
a
xa
dxxa 











 

221
2
22 1
.sin
2
ax
ax
xa
x
a
xa
dxxa
















221
2
22
.
2
sin
2

66. hitunglah integral tentu berikut yang
menggambarkan luas daerah setengah
lingkaran seperti pada gambar
y
x
 22
xay 
aa
A
luas yang diarsir, A
 dxxaA
a
a
22
 
Penggunaan
 
ax
ax
a
a
xa
x
a
xa
dxxaA
















 
221
2
22
.
2
sin
2

67. ax
ax
a
a
xa
x
a
xa
dxxa

















221
2
22
.
2
sin
2













 


















221
2
221
2
22
.
2
sin
2
.
2
sin
2
aa
a
a
aa
aa
a
a
aa
dxxa
a
a
   





 

 1sin
2
1sin
2
1
2
1
2
22 aa
dxxa
a
a
2
2
22 a
dxxa 

68. Contoh 20
carilah
2
9 x
dx


penyelesaian
misalkan
tx tan3 2/2/   tpada selang
  tdttddx 2
sec3tan3 
taxa sec22

tx sec33 22


69. dttdt
t
t
x
dx
sec
sec3
sec3
9
2
2  

ctt
x
dx


 tansecln
9 2
tx tan3
3
tan
x
t 
t
3
x
2
9 x
2
9
3
cos
x
t


dari aturan segitiga
3
9
sec
2
x
t



70. ctt
x
dx


 tansecln
9 2
c
xx
x
dx




 33
9
ln
9
2
2
c
xx
x
dx




 3
9
ln
9
2
2
cxx
x
dx


 3ln9ln
9
2
2
Kxx
x
dx



2
2
9ln
9

71. Contoh 21
carilah dx
xx 262
1
2


penyelesaian
2512262 22
 xxxx
222
512262  xxxx
  222
51262  xxx
1 xu
  222
5262  uxx
dxdu 

72. 25262
1
22



 u
du
dx
xx
misalkan tu tan5 pada selang 2/2/   t
 tddu tan5 dttdu 2
sec5
25tan2525 22
 tu
  ttu sec51tan2525 22

dt
t
t
u
du
sec5
sec5
25
2
2  


73. dttdt
t
t
u
du
sec5
sec5
sec5
25
2
2  

ctt
u
du


 tansecln
252
tu tan5
5
tan
u
t 
tu sec5252

5
25
sec
2


u
t
c
uu
u
du




 55
25
ln
25
2
2

74. c
uu
u
du




 5
25
ln
25
2
2
cuu
u
du


 5ln25ln
25
2
2
Kuu
u
du


 25ln
25
2
2
Kxxx
u
du


 1262ln
25
2
2

75. 4.Pengintegralan Parsial
Pendahuluan
vuy .jika dimana u dan v fungsi dari x
maka ).( vuddy 
vdudvudy  .
vdudydvu .
bila persamaan diintegrasi
vdudydvu  .

76. vduydvu  .
vduvudvu   ..
hal yang harus diperhatikan
pemilihan u dan dv, fungsi u harus lebih
sederhana dari dv

77. Contoh 22
Hitunglah
Penyelesaian
 dxxx cos.
misalkan xu 
dxdu 
dxxdv cos
maka
dxxdv cos 
xv sin
  duvvudxxx .cos.

78.   dxxxxdxxx sinsin.cos.
cxxxdxxx  )cos(sin.cos.
Jika pemilihan u dan dv tidak tepat akan
menghasilkan integral yang lebih rumit
dari contoh 7
 dxxx cos.
misalkan xu cos dxxdu sin
xdxdv 

79. xdxdv 
2
2
1
xv 
dxxdv  
maka
  duvvudxxx .cos.
  





 dxxxxxdxxx sin
2
1
2
1
.coscos. 22
Jika pemilihan u dan dv tidak tepat akan
menghasilkan integral yang lebih rumit

80. Contoh 23
Hitunglah
Penyelesaian

2
1
ln dxx
misalkan xu ln
dx
x
xddu
1
)(ln 
dxdv 
maka
dxdv  
xv 
  duvvudxx .ln
2
1

81. dx
x
xxxdxx
x
x  








2
1
2
1
2
1
1
.lnln
2
1
2
1
2
1
.lnln





x
x
x
x
xxxdxx
12ln2]12[]1ln1)2ln(2[ln
2
1
 dxx
 


2
1
2
1
2
1
.lnln dxxxdxx
x
x
12ln2]12[)]0(1)2ln(2[ln
2
1
 dxx

82. Contoh 24
Hitunglah
Penyelesaian
 dxxx sin.2
misalkan 2
xu 
dxxdu 2
dxxdv sin
maka
dxxdv sin 
xv cos
  duvvudxxx .sin.2

83.     dxxxxxdxxx 2coscossin. 22
 
    dxxxxxdxxx   cos2cossin. 22
    dxxxxxdxxx   cos2cossin. 22
dari contoh 9
cxxxdxxx  cossin.cos.
   cxxxxxdxxx  cossin.2cossin. 22
  Kxxxxxdxxx  cos2sin.2cossin. 22

84. LATIHAN 5
Hitunglah
dxex x
 ..1
 dxxx 3sin..2

85. 5. Integrasi fungsi rasional
Defenisi fungsi rasional
Fungsi rasional adalah hasil bagi dua fungsi
polinomial, fungsi rasional di bagi dua
1. Fungsi rasional sejati
yaitu derajat pembilang lebih kecil dari
penyebut
misal
 
84
22
2



xx
x
xf
2. Fungsi rasional tak sejati
yaitu derajat pembilang lebih besar dari
penyebut

86. misal
 
xx
xxx
xh
5
12
3
35



Contoh 24
Carilah
 
dx
x 
3
1
2
penyelesaian
 
dx
x 
3
1
2
misalkan 1 xu dxdu 

87.  
duudu
u
dx
x
3
33
2
2
1
2 
 

 
cudx
x






2
3
2
2
1
1
2
 
c
u
dx
x

 23
1
1
2
   
c
x
dx
x



 23
1
1
1
2

88. Contoh 25
Carilah dx
xx
x
84
22
2



penyelesaian
84
642
84
22
22





 xx
x
dx
xx
x
dx
xx
dx
xx
x
dx
xx
x
84
6
84
42
84
22
222








?
84
42
2



 dx
xx
x
misalkan 842
 xxu dxxdu 42 

89. u
u
du
x
du
u
x
dx
xx
x
ln
42
42
84
42
2







42 

x
du
dx
 84ln
84
42 2
2



 xxdx
xx
x
?
84
6
2

 dx
xx
 
dx
x
dx
xx 222
22
1
6
84
6


 

90. sehingga
c
a
x
aax
dx










1
22
tan
1
 
dx
x
dx
xx 222
22
1
6
84
6


 





 





 

 2
2
arctan3
2
2
arctan
2
1
6
84
6
2
xx
dx
xx
ingat
  K
x
xxdx
xx
x





 



 2
2
arctan384ln
84
22 2
2

91. Dekomposisi pecahan parsial (faktor linear)
Latihan menjumlahkan pecahan parsial
?
1
3
1
2



 xx
   
  11
1312
1
3
1
2





 xx
xx
xx
yang menarik adalah proses kebalikannya
yaitu dekomposisi suatu pecahan menjadi
suatu jumlah pecahan yang lebih sederhana

92. Contoh 26 (faktor linear yang berbeda)
dekomposisikan pecahan parsial berikut dan
carilah integrasinya
?
6
13
2



xx
x
      3232
13
6
13
2









x
B
x
A
xx
x
xx
x
   
  32
23
6
13
2





xx
xBxA
xx
x
   2313  xBxAx

93.    2313  xBxAx
3
7
;
5
8
 AB
BBxAAxx 2313 
   BAxBAx 2313 
  )(3 aBA 
  )(123 aBA 
eliminasi pers (a) dan (b)

94.    233313.33  BAx
5
8
58  BB
     22231232  BAx
atau
   2313  xBxAx
7
5
57  AA
      3
5/8
2
7/5
32
13
6
13
2









xxxx
x
xx
x

95.     





dx
x
dx
x
dx
xx
x
3
1
5
8
2
1
7
5
6
13
2
    cxxdx
xx
x



 3ln
5
8
2ln
7
5
6
13
2
Contoh 27 (faktor linear yang berbeda)
Carilah ?
32
35
23



 dx
xxx
x
penyelesaian
  
dx
xxx
x
dx
xxx
x
 




31
35
32
35
23

96.       3131
35






x
C
x
B
x
A
xxx
x
  
    
 
 
 3
1
1
331
31
35










x
xCx
x
xBx
x
xxA
xxx
x
      133135  xCxxBxxxAx
      133.333.33133.53  CBxAx
2
3
120018  CC
      133135  xCxxBxxxAx
        11)1.(31)1.(31113151  CBAx

97. 2
1
402  BB
      133135  xCxxBxxxAx
        10)0.(30)0.(30103050  CBAx
10033  AA
      3
2/3
1
2/11
31
35









xxxxxx
x
       





32
3
12
11
31
35
x
dx
x
dx
dx
x
dx
xxx
x
  
    cxxxdx
xxx
x



 3ln
2
3
1ln
2
1
ln
31
35

98. faktor linear yang berulang
untuk tiap faktor linear (ax+b) yang muncul k
kali dalam penyebut suatu pecahan rasional
yang baik terdapat suatu penjumlahan k
buah pecahan parsial berbentuk
k
k
bax
A
bax
A
bax
A
)()()( 2
21






misal
 
?
1
4

x
x
maka dekomposisi pecahan parsial dibuat
         4324
11111 







 x
D
x
C
x
B
x
A
x
x

99. Contoh 28 (faktor linear yang berulang)
Carilah
 
?
3
2

 dx
x
x
penyelesaian
     22
333 



 x
B
x
A
x
x
 
 
   222
33
3
3 




 x
B
x
xA
x
x
  BxAx  3
  BAx 
2
3333

100.   3333
2
 BBA
  BxAx 
2
3
1330  AA
  330  Ax
     22
333 



 x
B
x
A
x
x
     22
3
3
3
1
3 



 xxx
x
      




22
3
3
33 x
dx
x
dx
dx
x
x

101.       




22
3
3
33 x
dx
x
dx
dx
x
x
 
 
 
c
x
xdx
x
x



 3
3
3ln
3
2
Contoh 29
(beberapa faktor linear berbeda dan ada
yang berulang)
Carilah
  
?
13
1383
2
2



 dx
xx
xx

102. penyelesaian
       22
2
1133
1383








x
C
x
B
x
A
x
xx
 
      
  2
2
2
2
13
3131
3
1383





xx
xCxxBxA
x
xx
      31311383
22
 xCxxBxAxx
      31113111131.8)1(31
22
 CBAx
24008  CC

103.       31311383
22
 xCxxBxAxx
      3313331313)3.(8)3(33
22
 CBAx
0016132427  A
46416  AA
      31311383
22
 xCxxBxAxx
      3010301013)0.(8)0(30
22
 CBAx
CBA 3313 
163413  BB

104.        22
2
1
2
1
1
3
4
3
1383









xxxx
xx
       22
2
1
2
1
1
3
4
3
1383









xxxx
xx
        







dx
x
dx
x
dx
x
dx
x
xx
22
2
1
1
2
1
1
3
1
4
3
1383
 
   
 
c
x
xxdx
x
xx





 1
2
1ln3ln4
3
1383
2
2

105. Dekomposisi pecahan parsial (faktor kuadratik)
Dalam memfaktorkan penyebut suatu
pecahan, jika kita mungkin mendapatkan
beberapa faktor kuadrat, misalnya seperti
(x2 +1), yang tak dapat lagi diuraikan menjadi
faktor-faktor linier tanpa mengenalkan
bilangan kompleks, maka dekomposisi
pecahan parsial di buat
)( 2
cbxax
BAx



106. Contoh 30 (faktor kuadrat tunggal)
dekomposisikan pecahan parsial dan cari
integrasinya
 
?
)1(14
136
2
2



xx
xx
    )1(14)1(14
136
22
2







x
CBx
x
A
xx
xx
 
 
  )1(14
14).()1(
)1(14
136
2
2
2
2





xx
xCBxxA
xx
xx

107.  
 
  )1(14
14).()1(
)1(14
136
2
2
2
2





xx
xCBxxA
xx
xx
 14).()1(136 22
 xCBxxAxx
 1)4/1.(4).4/1.(1
16
1
1
4
1
3
4
1
6
4
1
2


















 CBAx
2
16
17
16
16
16
12
16
6
 AA
 14).()1(136 22
 xCBxxAxx
 10).0()10(210  Cx
 10).0()10(21  C 1C

108.  14).()1(136 22
 xCBxxAxx
       3).1(112113161
2
 Bx
133410  BB
    )1(14)1(14
136
22
2







x
CBx
x
A
xx
xx
    )1(
1
14
2
)1(14
136
22
2







x
x
xxx
xx
     






dx
x
x
dx
x
dx
xx
xx
)1(
1
14
1
2
)1(14
136
22
2

109.      







dx
x
dx
x
x
dx
x
dx
xx
xx
)1(
1
)1(14
1
2
)1(14
136
222
2
     







dx
x
dx
x
x
x
dx
dx
xx
xx
)1(
1
)1(
2
2
1
14
4
2
1
)1(14
136
222
2
 
  cxarcxxdx
xx
xx



 tan)1ln(
2
1
14ln
2
1
)1(14
136 2
2
2

110. faktor kuadrat berulang
untuk tiap faktor kuadratik yang tak dapat
direduksi ax2+bx+c yang muncul m kali
dalam penyebut pecahan rasional yang baik
maka dekomposisi pecahan mempunyai
bentuk
m
mm
cbxax
BxA
cbxax
BxA
cbxax
BAx
)()()( 222
11
2









misal
?
)1(
136
32
2



x
xx
pecahan parsialnya
3222232
2
)1()1()1()1(
136











x
FEx
x
DCx
x
BAx
x
xx

111. Contoh 31
cari integrasinya
  

dx
xx
xx
22
2
)2(3
22156
penyelesaian
    22222
2
)2()2(3)2(3
22156










x
EDx
x
CBx
x
A
xx
xx
 
      
  22
222
22
2
)2(3
33)2()2(
)2(3
22156





xx
xEDxxxCBxxA
xx
xx
      33)2()2(22156 2222
 xEDxxxCBxxAxx
00)29(2245543 2
 Ax
1121121  AA

112. ECAx 36422)0(15)0(60 2

)1(1836  EC
13441212922)1(15)1(61 2
 EDCBAx
)2(4441212  EDCB
134412121.9  EDCB
      30030)20(0)20(221560 22
 ECAxxx
      33)2()2(22156 2222
 xEDxxxCBxxAxx
      33)2()2(22156 2222
 xEDxxxCBxxAxx
      3131)21()21(221561 22
 EDCBAxxx

113. DEBCA 2266943 
      33)2()2(22156 2222
 xEDxxxCBxxAxx
      3131)21()21(221561 22
 EDCBAxxx
)3(342266  EDCB
eliminasi (2)(3)
)2(4441212  EDCB
)3(342266  EDCB 2
1
x
x
4441212  EDCB
68441212  EDCB

)4(72824  EC

114. eliminasi (1)(4)
)1(1836  EC
)4(72824  EC 1
4
x
x
721224  EC
72824  EC

004  EE
)1(180.36 C
3186  CC

115.       33)2()2(22156 2222
 xEDxxxCBxxAxx
      33333)29(3)29(221563 22
 EDCBAxxx
   EDCB 618661981.12131 
    9061866198  EDCB
    90183.66198  DB
    )5(28818198  DB
dari pers (3) sub C = 3, E= 0
)3(1626  DB

116. eliminasi (5)(3)
    )5(28818198  DB
)3(1626  DB 9
4
x
x
    28818198  DB
1441854  DB

1144144  BB
dari (3) sub B = -1 )3(1626  DB
5102  DD

117.    
dx
x
x
dx
x
x
dx
x
dx
xx
xx
22222
2
)2(
5
)2(
3
3
1
)2(3
22156











   
dx
x
x
dx
x
x
dx
x
dx
xx
xx
22222
2
)2(
5
)2(
3
3
1
)2(3
22156










   
dx
x
x
x
dx
x
dxx
x
dx
dx
xx
xx
222222
2
)2(
2
2
5
)2(
3
)2(
.2
2
1
3)2(3
22156











 
  c
x
x
arcxxdx
xx
xx











 )2(
1
2
5
2
tan
2
3
)2ln(
2
1
3ln
)2(3
22156
2
2
22
2

118. LATIHAN 6
Hitunglah
  dx
xx
xx
912
3632
.1 2
2



   
dx
xxx
xx
32312
327
.2
2


