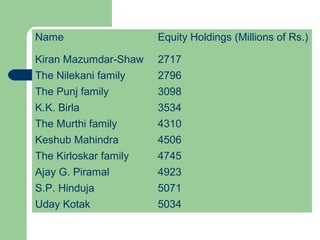
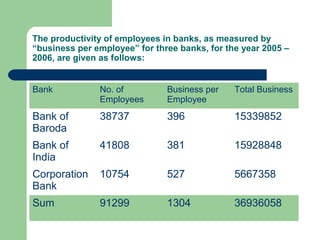
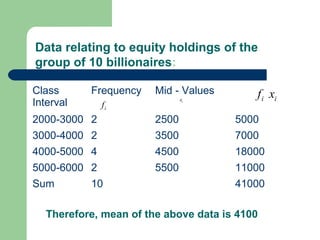
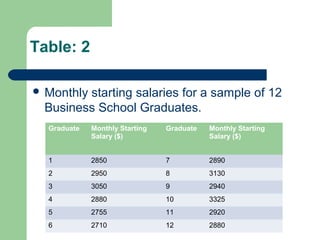
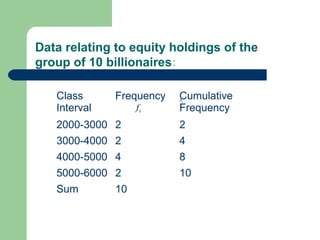
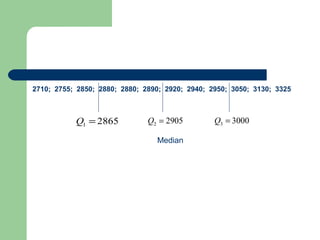
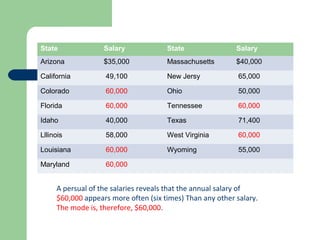
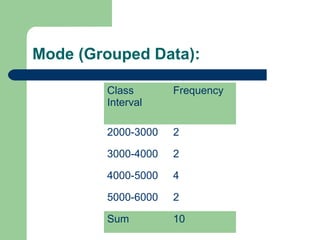
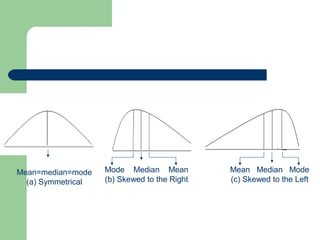
The document discusses various measures of central tendency including the mean, median, and mode. It provides definitions and formulas for calculating each measure, as well as examples of how to calculate the mean for grouped and ungrouped data, the median for grouped and ungrouped data, percentiles, quartiles, and the relationship between the mean, median, and mode. The key information is that measures of central tendency describe the central or typical value in a data set and include the mean, median, and mode.