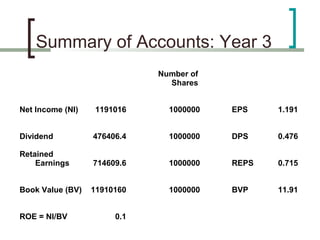
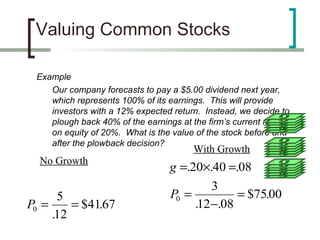
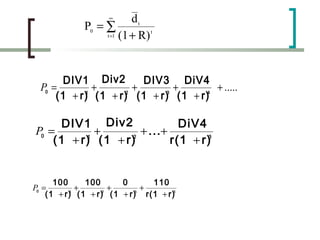
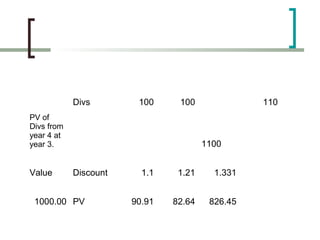
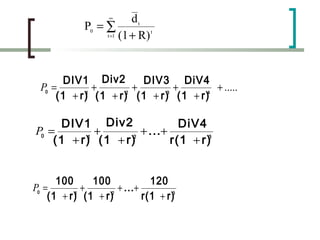
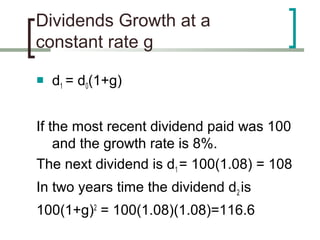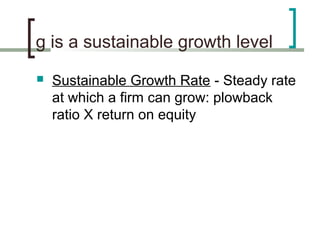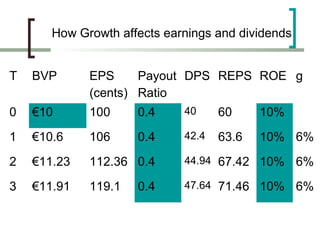
The document discusses various methods for valuing bonds and common stocks, including: - Bond valuation using the present value of expected cash flows - Dividend discount models for valuing common stocks based on the present value of expected future dividends - Constant growth dividend discount models that incorporate a constant dividend growth rate - How the sustainable growth rate is determined by a company's return on equity and plowback ratio

1. Valuation of Bonds and
Equities
 The value of any business asset
depends on its expected future cash
flows.
 If you buy a bond you are effectively
buying a stream of cash flows.

2. Bond with face (nominal) value of €100: coupon
rate of 8% with 5 years to maturity.
If the yield to redemption on this type of
bond is 10% at the moment how much
should you pay for it?
0 1 2 3 4 5
? 8 8 8 8 108

3. Get the PV of the cash flows
of the bond @ 10%
Annuity of €8 p.a. for 5 years
PV = 8 X 3.791 = 30.33
€100 at the end of 5 years
PV = 100 X 0.621 = 62.10
The value of the bond is €92.43

4. Topics Covered
 How To Value Common Stock
 Capitalization Rates
 Stock Prices and EPS

5. Stocks & Stock Market
Common Stock - Ownership shares in a
publicly held corporation.
Secondary Market - market in which
already issued securities are traded by
investors.
Dividend - Periodic cash distribution from
the firm to the shareholders.
P/E Ratio - Price per share divided by
earnings per share.

6. Stocks & Stock Market
Book Value - Net worth of the firm
according to the balance sheet.
Liquidation Value - Net proceeds that
would be realized by selling the firm’s
assets and paying off its creditors.
Market Value Balance Sheet - Financial
statement that uses market value of
assets and liabilities.

7. Valuing Common Stocks
Expected Return - The percentage yield that
an investor forecasts from a specific
investment over a set period of time.
Sometimes called the market capitalization
rate or the cost of capital.
E ( Div1 ) + E ( P ) − P0
Expected Return = r = 1
P0

8. Valuing Common Stocks
Example: If Fledgling Electronics is selling for
$100 per share today and is expected to sell
for $110 one year from now, what is the
expected return if the dividend one year
from now is forecasted to be $5.00?
5 + 110 − 100
Expected Return = = .15
100

9. Valuing Common Stocks
The formula can be broken into two
parts.
Dividend Yield + Capital Appreciation
Div1 P − P0
Expected Return = r = + 1
P0 P0

10. What is the value of a share?
If an investor buys a share it is worth the PV of
the future cash flows it gives her.
If she plans to hold the share for one year
(period). (Note I have dropped E() for
convenience.)
P + D1
1
P =
0
(1 +r )

11. Valuing Common Stocks
Example
Current forecasts are for XYZ Company to
pay dividends of $3, $3.24, and $3.50 over
the next three years, respectively. At the
end of three years you anticipate selling
your stock at a market price of $94.48. What
is the price of the stock given a 12%
expected return?

12. Valuing Common Stocks
Example
Current forecasts are for XYZ Company to pay dividends of
$3, $3.24, and $3.50 over the next three years, respectively.
At the end of three years you anticipate selling your stock at a
market price of $94.48. What is the price of the stock given a
12% expected return?
3.00 3.24 350 + 94.48
.
PV = + +
(1+.12) (1+.12)
1 2
(1+.12) 3
PV = $75.00

13. Value of Shareholders Funds
 If an investor buys a share it is worth
the PV of the future cash flows it gives
her. If she plans to hold the share for
2 years the following formula applies.
Div1 Div2 + P2
P0 = +
(1 + r )1
(1 + r ) 2

14. If the investor she sells to at t2 plans
to hold the share for H years its value
is :
Div3 Div4 DivH + PH
P2 = 1
+ 2
+ ...+ H−2
(1 + r) (1 + r) (1 + r)
Substituting this into the previous equation gives:

15. Substituting this into the previous equation gives
Div1 Div2 Div H + PH
P0 = + +...+
(1 + r ) (1 + r )
1 2
(1 + r ) H
This logic can be applied to the investor who buys the share
in year H and so on terminal value PH is so far in the
future that it can be until the ignored. Thus, the value
of a share is theoretically equal to the PV of all the future
dividends discounted at the cost of capital

16. The Dividend Discount Model:
Assume an investor holds a share for one year and sells
Let (1+r) = ρE To another investor who also holds the share for 1 year..
d 3 + V3 d 4 + V4
V2 = V3 = ...........
d 2 + V2 ρE ρE
d1 + V1 V1 =
V0 = ρE
ρE
d V ∞
d d V d d d V dt
V0 = 1 + 1
ρE ρE
= 1 + 2 + 22 = 1 + 2 + 3 + 3 ... = ∑
ρE ρE ρE
2
ρE ρE ρE ρE
2 3 3
t =1 ρE
t
4 d t TV4
V0 = ∑ t + 4
t =1 ρ ρE
E

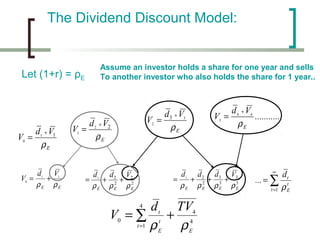
17. The Basic Dividend Valuation
Model is:
~ ]
∞
E t [ d t+τ
Pt = ∑ τ
(PVED)
τ =1
RF
The value of a share is the present value of all
the dividends that It pays to infinity.

18. Valuing Common Stocks
Dividend Discount Model - Computation of
today’s stock price which states that share
value equals the present value of all
expected future dividends.

19. Making the Basic DDM
practical
If we assume all dividends are the same
forever this implies we forecast no growth
and will then value the stock as a
PERPETUITY.
D1
P0 =
r

20. Valuing Common Stocks
This essentially assumes that the company
does not grow.
No earnings are retained so all earnings are
paid out as dividends.
D1 EPS1
Perpetuity = P0 = or
r r
Assumes all earnings are
paid to shareholders.

21. This is essentially the P/E ratio
method of valuing a stock
Re-arranging the above equation we get
EPS1
P0 =
r
EPS1 1 P0
⇒r = or = =P
P0 r EPS1 E

22. Constant Dividend Model
 This is obviously unrealistic since it
assumes that no earnings are retained
and there is no growth.
 Accordingly, we need to adjust this
formula for the value of growth.

23. Constant Growth Model
Constant Growth DDM - A version of the dividend
growth model in which dividends grow at a constant
rate (Gordon Growth Model).
Div1
P0 =
r −g

24. Dividends Growth at a
constant rate g
 d1 = d0(1+g)
If the most recent dividend paid was 100
and the growth rate is 8%.
The next dividend is d1 = 100(1.08) = 108
In two years time the dividend d2 is
100(1+g)2 = 100(1.08)(1.08)=116.6

25. Where does g come from?
 It come from retained earnings which
are reinvested at the cost of capital.
 This increases subsequent earnings
and dividends.

26. Valuing Common Stocks
 If a firm elects to pay a lower dividend, and
reinvest the funds, the stock price may
increase because future dividends may be
higher.
Payout Ratio - Fraction of earnings paid out as
dividends
Plowback (Ploughback) Ratio - Fraction of
earnings retained by the firm.

27. Valuing Common Stocks
Growth can be derived from applying
the return on equity to the percentage
of earnings plowed (ploughed) back
into operations.
g = return on equity X plough back ratio
The ploughback ratio is 1 – payout ratio

28. g is a sustainable growth level
 Sustainable Growth Rate - Steady rate
at which a firm can grow: plowback
ratio X return on equity

29. Notation
BVP: Book value per share
Payout Ratio: The proportion of earnings paid
out. DPS=EPS X Payout Ratio
REPS: Retained Earnings Per Share: that part
of earnings per share not paid in dividends
and ploughed back into the business = EPS
X Ploughback Ratio
ROE: Return on Equity = EPS/BVP

30. Example
An all equity company has 1,000,000
shares and a book value of €10m
The BVP is €10
If we assume the ROE is 10% the EPS is
0.1 X 10 = €1 or 100 cent
If we assume the payout ratio is 40% the
DPS is 40 cent.

31. Summary of Accounts: year 0
Number of Shares
Net Income (NI) 1000000 1000000 EPS 1
Dividend 400000 1000000 DPS 0.4
Retained
Earnings 600000 1000000 REPS 0.6
Book Value
(BV) 10000000 1000000 BVP 10
ROE = NI/BV 0.1

32. How Growth affects earnings and dividends
T BVP EPS Payout DPS REPS ROE g
(cents) Ratio
0 €10 100 0.4 40 60 10%
1 €10.6 106 0.4 42.4 63.6 10% 6%
2 €11.23 112.36 0.4 44.94 67.42 10% 6%
3 €11.91 119.1 0.4 47.64 71.46 10% 6%

33. Summary of Accounts: Year 3
Number of
Shares
Net Income (NI) 1191016 1000000 EPS 1.191
Dividend 476406.4 1000000 DPS 0.476
Retained
Earnings 714609.6 1000000 REPS 0.715
Book Value (BV) 11910160 1000000 BVP 11.91
ROE = NI/BV 0.1

34. Valuing Common Stocks
Example
Our company forecasts to pay a
$5.00 dividend next year, which
represents 100% of its earnings.
This will provide investors with a
12% expected return. Instead,
we decide to plough back 40% of
the earnings at the firm’s current
return on equity of 20%. What is
the value of the stock before and
after the plowback decision?

35. Valuing Common Stocks
Example
Our company forecasts to pay a $5.00 dividend next year,
which represents 100% of its earnings. This will provide
investors with a 12% expected return. Instead, we decide to
plough back 40% of the earnings at the firm’s current return
on equity of 20%. What is the value of the stock before and
after the plowback decision?
No Growth With Growth
5
P0 = = $41.67
.12

36. Valuing Common Stocks
Example
Our company forecasts to pay a $5.00 dividend next year,
which represents 100% of its earnings. This will provide
investors with a 12% expected return. Instead, we decide to
plough back 40% of the earnings at the firm’s current return
on equity of 20%. What is the value of the stock before and
after the plowback decision?
With Growth
No Growth
g =.20×.40 =.08
3
5 P0 = = $75.00
P0 = = $41.67 .12 −.08
.12

37. Valuing Common Stocks
Example - continued
If the company did not plowback some
earnings, the stock price would remain at
$41.67. With the plowback, the price rose
to $75.00.
The difference between these two numbers
(75.00-41.67=33.33) is called the Net
Present Value of Growth Opportunities
(PVGO).

38. Valuing Common Stocks
Net Present Value of Growth
Opportunities (PVGO) - Net present
value of a firm’s future investments.

39. Value of a share with growth
EPS1
P0 = + PVGO
r
AND
P 1 PVGO
= +
E r EPS1

40. Examples – using a Dividend
Discount model to Value shares
 How much is a share worth if it yield
DPS of 100 cent forever. The cost of
capital or expected rate of return is
10%
 Answer: 100/0.1 = 1000 cent or €10

41. Suppose the company did not
pay a Div in year 3
 It reinvests the 100 cent per share at
10%.
 What happens to the value of the share?
 First need to consider what happens to
dividends
 Assume that dividends are reinvested at
the cost of capital i.e. 10%

42. Reinvestment of Profits in year 3
 Dividends in year three are zero
 Dividends from year 4 onwards
increase to 110 cent per annum. (The
100 cent yields are return of 10%)
 Accordingly we have dividends of 100
cent for years one and two. Zero divs
for year 3 and a perpetuity of 110 cent
from year 4 onwards.

43. ∞ dt
P0 = ∑
t =1 (1 + R)
t
DIV1 Div2 DIV3 DiV4
P0 = + + + + .....
(1 + r) (1 + r) (1 + r) (1 + r)
1 2 3 4
DIV1 Div2 DiV4
P0 = + + ... +
(1 + r) (1 + r)
1 2
r(1 + r)3
100 100 0 110
P0 = + + +
(1 + r) (1 + r)2 (1 + r)3 r(1 + r)3
1

44. Divs 100 100 110
PV of
Divs from
year 4 at
year 3. 1100
Value Discount 1.1 1.21 1.331
1000.00 PV 90.91 82.64 826.45

45. Why is there no change in
value?
 Because the investment of
retained earnings only yields the
same rate of return as the cost of
equity.
 We could use the formula
EPS1
P0 = + PVGO
r
100
P0 = + 0 =100
0 .1

46. Real Growth Opportunity
 What if the company did not pay any
Divs in year three but invested in a
positive NPV project
 For example a project yielding 20 cent
per share per annum forever
beginning in year 4

47.  NPV of the project
is NPV = − 100 +
20
= 100
0.1

48. But this NPV is at year 3
 NPV now is 100 x 0.7513 = 75.13
100
P0 = + 75.13 = 1075.13 cent
0.1

49. ∞ dt
P0 = ∑
t =1 (1 + R)
t
DIV1 Div2 DIV3 DiV4
P0 = + + + + .....
(1 + r) (1 + r) (1 + r) (1 + r)
1 2 3 4
DIV1 Div2 DiV4
P0 = + + ... +
(1 + r) (1 + r)
1 2
r(1 + r)3
100 100 120
P0 = + + ... +
(1 + r) (1 + r)
1 2
r(1 + r)3

50. 4 to
1 2 3 infinity
Divs 100 100 0 120
PV of Divs
from year 4 at
year 3. 1200
Discount
Value Factor 1.1 1.21 1.331
1075.13 PV 90.91 82.64 901.58