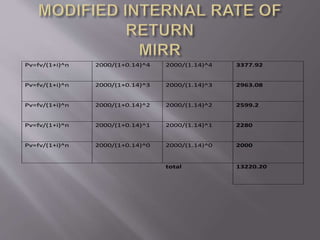
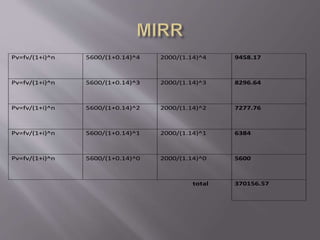
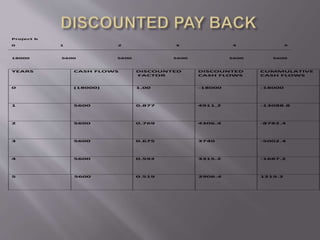
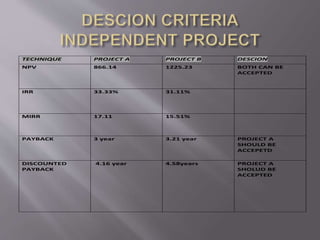
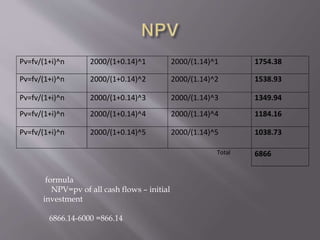
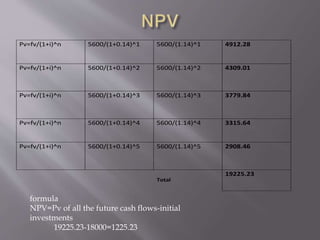
This document discusses various capital budgeting techniques including net present value (NPV), internal rate of return (IRR), modified internal rate of return (MIRR), payback period, and discounted payback period. It provides examples of calculating each of these metrics for two hypothetical projects, Project A and Project B. Based on the different criteria, it determines that Project A should be accepted over Project B in most cases due to having a higher NPV, IRR, MIRR, and shorter payback and discounted payback periods.

1. NPV.
IRR.
MIRR.
PAYBACK.
DISCOUNTED PAYBACK.

2.  Net present value is the sum of all the
discounted cash flows.
 Net Present Value (NPV) is the difference
between the present value of cash inflows and
the present value of cash outflows. NPV is used
in capital budgeting to analyze the profitability
of a projected investment or project.
 Positive npv presents earning
negative npv presents deficit

3.  CALCULATE NPV
 PROJECT A
 Assume that
 A project with cash flows of 2000 for 5 years
 Wacc 14%
 Initial investment of 6000
 Calculate Npv for5 years.

4. Pv=fv/(1+i)^n 2000/(1+0.14)^1 2000/(1.14)^1 1754.38
Pv=fv/(1+i)^n 2000/(1+0.14)^2 2000/(1.14)^2 1538.93
Pv=fv/(1+i)^n 2000/(1+0.14)^3 2000/(1.14)^3 1349.94
Pv=fv/(1+i)^n 2000/(1+0.14)^4 2000/(1.14)^4 1184.16
Pv=fv/(1+i)^n 2000/(1+0.14)^5 2000/(1.14)^5 1038.73
Total 6866
formula
NPV=pv of all cash flows – initial
investment
6866.14-6000 =866.14

5.  CALCULATE NPV
 PROJECT B
 Assume that
 A project with cash flow of 5600 for5 Years
 Wacc 14 %
 Initial investment 18000
 Calculate Npv for 5 years

6. Pv=fv/(1+i)^n 5600/(1+0.14)^1 5600/(1.14)^1 4912.28
Pv=fv/(1+i)^n 5600/(1+0.14)^2 5600/(1.14)^2 4309.01
Pv=fv/(1+i)^n 5600/(1+0.14)^3 5600/(1.14)^3 3779.84
Pv=fv/(1+i)^n 5600/(1+0.14)^4 5600/(1.14)^4 3315.64
Pv=fv/(1+i)^n 5600/(1+0.14)^5 5600/(1.14)^5 2908.46
Total
19225.23
formula
NPV=Pv of all the future cash flows-initial
investments
19225.23-18000=1225.23

7.  IRR is another commonly used as an NPV
alternative.
 Internal rate of return (IRR) is the interest rate
at which the net present value of all the cash
flows (both positive and negative) from a
project or investment equal zero.

8.  CALCULATE IRR for project A
 A firm with 14 % wacc
 Annual cash flows 2000
 Initial investment 6000
Find IRR
Formula
IRR=annual cash flows/initial investment
2000/6000 = 33.33%

9.  CALCULATE IRR FOR PROJECT B
 A firm with 14 % wacc
 Annual cash flows 5600
 Initial investment 18000
Find IRR
Formula
IRR=annual cash flows/initial investment
5600/18000 = 31.11%

10.  IRR=A+{C/C-D]*(B-A).
 Suppose
 A=low discount rate
 B=high discount rate
 C=npv @ low discount rate
 D=npv @high discount rate.
 WACC 10%
 A 10%
 B 20%
 C 78.8
 D -10.1

11.  IRR = 10% +[78.8/78.8-(-10.1) * (20%-10%)
 IRR = 10%+[78.8/78.8+10.1] * (20%-10%)
 IRR = 10%+[78.8/88.9] * (20%-10%)
 IRR =10% + 8.86
 IRR = 18.86
 IF IRR > MINIMUM DESIREDTHE RATE OF RETURN ACCEPTED.
 IF IRR < MINIMUM DESIREDTHE RATE OF RETURN.
 REJECTED.
 IF IRR =MINIMUM DESIREDTHE RATE OF RETURN. ACCEPTED

12.  MIRR is the internal rate of return of an
investment that is modified to account for the
difference between re-investment rate and
investment return.
 The decision rule for MIRR is very similar to
IRR, i.e. an investment should be accepted if
the MIRR is greater than the cost of capital.

13.  CALCULATE MIRR for project A
 A firm cash flows are 2000 for 5 years
 Wacc = 14%
 Initial investment 6000.

14. Pv=fv/(1+i)^n 2000/(1+0.14)^4 2000/(1.14)^4 3377.92
Pv=fv/(1+i)^n 2000/(1+0.14)^3 2000/(1.14)^3 2963.08
Pv=fv/(1+i)^n 2000/(1+0.14)^2 2000/(1.14)^2 2599.2
Pv=fv/(1+i)^n 2000/(1+0.14)^1 2000/(1.14)^1 2280
Pv=fv/(1+i)^n 2000/(1+0.14)^0 2000/(1.14)^0 2000
total 13220.20

15.  Formula
 Pv of it’s cost =Pv of it’s terminal value.
 6000=13220.20/(1+MIRR)^5
 (1+MIRR)^5=13220.20/6000
 (1+MIRR)^5=2.2033
 (1+MIRR)^5*1/5 =(2.2033)^1/5
 (1+MIRR) = (2.2033)^0.2
 1+MIRR = 1.1711
 MIRR=1.1711-1
 MIRR =17.11%

16.  CALCULATE MIRR for project B
 A firm cash flows are 5600 for 5 years
 Wacc = 14%
 Initial investment 18000.

17. Pv=fv/(1+i)^n 5600/(1+0.14)^4 2000/(1.14)^4 9458.17
Pv=fv/(1+i)^n 5600/(1+0.14)^3 2000/(1.14)^3 8296.64
Pv=fv/(1+i)^n 5600/(1+0.14)^2 2000/(1.14)^2 7277.76
Pv=fv/(1+i)^n 5600/(1+0.14)^1 2000/(1.14)^1 6384
Pv=fv/(1+i)^n 5600/(1+0.14)^0 2000/(1.14)^0 5600
total 370156.57

18.  Formula
 Pv of it’s cost =Pv of it’s terminal value.
 18000=37016.57/(1+MIRR)^5
 (1+MIRR)^5=37016.57/18000
 (1+MIRR)^5=2.0564
 (1+MIRR)^5*1/5 =(2.0564)^1/5
 (1+MIRR) = (2.0564)^0.2
 1+MIRR = 1.1551
 MIRR=1.1551-1
 MIRR =15.51%

19. Payback is defined as the length of time it takes the
net cash revenue / cash cost savings of a project to
payback the initial investment.
Calculate payback
PROJECT A
A firm with cash flows of 2000 each year for 5 year
Calculate pay back period
0 1 2 3 4 5
6000 2000 2000 2000 2000 2000
FORMULA
PAYBACK=NUMBER OF YEAR+RECOVERY PORTION OF CASH FLOWS/CASH FLOWS DURING
YEAR.
Pay back =3 YEARS+0/2000
Payback = 3 YEARS

20. PROJECT B
A firm with cash flows of 5600 each year for 5 year
Calculate pay back period
0 1 2 3 4 5
18000 5600 5600 5600 5600 5600
FORMULA
PAYBACK=NUMBER OF YEAR+RECOVERY PORTION OF CASH FLOWS/CASH FLOWS DURING
YEAR.
Pay back =3 YEARS+1200/5600
Payback = 3.21 YEARS

21.  The discounted payback is defined as the
length of time it takes the discounted net cash
revenue/cost savings of a project to payback
the initial investment.

22. Project a
0 1 2 3 4 5
6000 2000 2000 2000 2000 2000
DISCOUNTED PAY BACK
YEARS CASH FLOWS DISCOUNTED
FACTOR
DISCOUNTED
CASH FLOW
CUMMULATIVE
CASH FLOWS
0 (6000) 1.00 -6000 -6000
1 2000 0.877 1754 -4246
2 2000 0.769 1538 -2708
3 2000 0.675 1350 -1358
4 2000 0.592 1184 -174
5 2000 0.519 1038 864
FORMULA
Payback = number of years + recovery of portion of cash flow/cash flow during that year.
= 4 years+174/1038
= 4.16 year

23. Project b
0 1 2 3 4 5
18000 5600 5600 5600 5600 5600
YEARS CASH FLOWS DISCOUNTED
FACTOR
DISCOUNTED
CASH FLOWS
CUMMULATIVE
CASH FLOWS
0 (18000) 1.00 -18000 -18000
1 5600 0.877 4911.2 -13088.8
2 5600 0.769 4306.4 -8782.4
3 5600 0.675 3740 -5002.4
4 5600 0.592 3315.2 -1687.2
5 5600 0.519 2906.4 1219.2

25. TECHNIQUE PROJECT A PROJECT B DESCION
NPV 866.14 1225.23 BOTH CAN BE
ACCEPTED
IRR 33.33% 31.11%
MIRR 17.11 15.51%
PAYBACK 3 year 3.21 year PROJECT A
SHOULD BE
ACCEPETD
DISCOUNTED
PAYBACK
4.16 year 4.58years PROJECT A
SHOLUD BE
ACCEPTED

26. TECHNIQUE PROJECT A PROJECT B DESCION
NPV 866.14 1225.23 PROJECT“B”HAS
NPV GREAATER
THEN “B” PROJECT
“A” “B”SHOULD BE
ACCEPETED
IRR 33.33% 31.11% ON BASIS OF IRR
PROJECT A SHOULD
BE ACCEPETED
MIRR 17.11% 15.51% MIRR OF PROJECT
“A” IS HIGHER THEN
PROJECT “B”
PROJECT “B”
SHOULD BE
ACCEPTED
PAYBACK 3 year 3.21 year PROJECT “A”
SHOULD BE
ACCEPETD IT WILL
GIVES RETURN IN
LESS TIME THEN “B”
PROJECT
DISCOUNTED
PAYBACK
4.16 year 4.58years PROJECT “A”
SHOLUD BE
ACCEPTED IT
RECOVERS INITIAL
INVESTMENT IN
LESS TIME THEN “B”
PROJECT

27.  THANK YOU

28.  ANY QUESTIONS