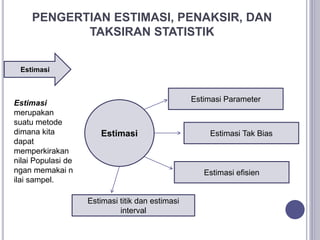
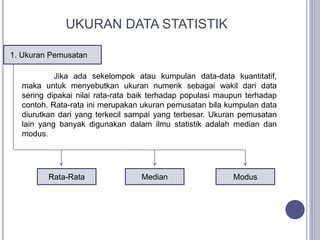
1. Dokumen tersebut membahas beberapa konsep dasar dalam statistika seperti definisi statistika dan statistika, parameter dan statistik, populasi dan sampel, estimasi, penaksiran, dan ukuran-ukuran data statistik seperti rata-rata, median, modus, dan koefisien variasi.

1. Kelompok
1. Fika Nur Fidiyanti (6661160028)
2. Siti Sahati (6661160041)
3. Ahmad Mahdi (6661160064)
4. Gladys Anggriana (6661160066)

2. PENGERTIAN STATISTIK VS. STATISTIKA
Pengertian statistik itu sendiri berasal dari kata state
(Yunani) yaitu negara dan digunakan untuk urusan negara.
Dari uraian ini dapat dikatakan bahwa statistik adalah
rekapitulasi dari fakta yang berbentuk angka-angka disusun
dalam bentuk tabel dan diagram yang mendeskripsikan suatu
permasalahan.
Statistika (statistic) adalah ilmu terdiri dari teori dan
metoda yang merupakan cabang dari matematika terapan dan
membicarakan tentang bagaimana mengumpulkan data,
bagaimana meringkas data, mengolah data menyajikan data,
bagaimana menarik kesimpulan dari hasil analisis, bagaimana
menentukan keputusan dalam batas-batas resiko tertentu
berdasarkan startegi yang ada.

3. PENGERTIAN PARAMETER
Parameter merupakan ukuran-ukuran yang berlaku pada
populasi. Simbol parameter θ (baca: tetha), sedangkan statistik
merupakan ukuran-ukuran yang berkenaan dengan sampel.
Parameter juga memiliki pengertian sekumpulan angka angka
yang dapat memberikan gambaran mengenai keadaan suatu
keadaan/gejala.
Yang membedakan Statistik dan Parameter adalah adalah
data awal yang diolah untuk dijadikan Informasi. Statistik
menggunakan Sampel sebagai data awalnya, sedangkan
parameter menggunakan populasi.

4. PENGERTIAN POPULASI DAN SAMPEL
Populasi merupakan subyek
penelitian. Populasi itu bukan hanya
orang, tetapi juga obyek dan benda-benda
alam yang lain. Populasi juga bukan
sekedar jumlah yang ada pada
obyek/subyek yang dipelajari, tetapi
meliputi seluruh karakteristik/sifat yang
dimiliki oleh subyek atau obyek itu.
Jadi dapat ditarik kesimpulan bahwa
populasi merupakan Objek atau Subjek
yang berada pada Suatu Wilayah dan
Memenuhi Syarat – Syarat tertentu
berkaitan dengan Masalah Penelitian.”
Pengertian
Populasi

5. Sampel (menurut Sugiyono,
2003 ; 56) adalah sebagian dari
jumlah dan karakteristik yang
dimiliki oleh populasi tersebut. Bila
populasi besar, dan peneliti tidak
mungkin mempelajari semua yang
ada pada populasi, maka peneliti
dapat menggunakan sample yang
diambil dari populasi itu. Semua
yang dipelajari dari sample itu,
kesimpulannya akan diberlakukan
untuk Populasi. Oleh karena itu,
Sampel yang diambil dari Populasi
harus benar – benar Representatif.
Sampel

6. PENGERTIAN ESTIMASI, PENAKSIR, DAN
TAKSIRAN STATISTIK
Estimasi
Estimasi Parameter
Estimasi Tak Bias
Estimasi efisien
Estimasi titik dan estimasi
interval
Estimasi
merupakan
suatu metode
dimana kita
dapat
memperkirakan
nilai Populasi de
ngan memakai n
ilai sampel.
Estimasi

7. Penaksiran
Deinisi Penaksiran :
• Penaksir Ô dikatakan penaksir tak bias jika rata-rata semua harga Ô
yang mungkin akan sama dengan 0. Dalam bahasa ekspektasi
ditulis ε (Ô) = 0. Penaksir yang tidak tak bias disebut penaksir bias.
• Penaksir bervarians minimum ialah penaksir dengan varians terkecil
di antara semua penaksir untuk parameter yang sama. Jika Ô1 dan
Ô2 dua penaksir untuk 0 di mana varians untuk Ô1 lebih kecil dari
varians untuk Ô2 maka Ô1 merupakan penaksir bervarians
minimum.
• Misalkan Ô penaksir untuk 0 yang dihitung berdasarkan sebuah
sampel acak berukuran n. Jika ukuran sampel n makin besar
mendekati ukuran populasi menyebabkan Ô mendekati 0, maka Ô
disebut penaksir konsisten.
• Penaksir yang tak bias dan bervarians minimum dinamakan
penaksir terbaik.

8. UKURAN DATA STATISTIK
Kegiatan pengumpulan data dimaksudkan untuk
mengetahui karakteristik dari data-data itu. Ada banyak
macam ukuran statistik yang digunakan untuk
menjelaskan dan menguraikan data-data yang berhasil
dikumpulkan.
Cara memperoleh data yang diperlukan
keseluruhannya bergantung pada kondisi dasarnya. Bila
kondisi memungkinkan, pengumpulan data dilaksanakan
secara sensus. Ini terjadi bila setiap individu yang
membentuk populasi yang sedang diamati dicatat untuk
dilakukan penelitian, akan tetapi bila tidak memungkinkan,
biasanya dilakukan dengan pencuplikan contoh terhadap
sebagian yang diambil dari populasi.

9. UKURAN DATA STATISTIK
1. Ukuran Pemusatan
Jika ada sekelompok atau kumpulan data-data kuantitatif,
maka untuk menyebutkan ukuran numerik sebagai wakil dari data
sering dipakai nilai rata-rata baik terhadap populasi maupun terhadap
contoh. Rata-rata ini merupakan ukuran pemusatan bila kumpulan data
diurutkan dari yang terkecil sampai yang terbesar. Ukuran pemusatan
lain yang banyak digunakan dalam ilmu statistik adalah median dan
modus.
Rata-Rata Median Modus

10. Rata-Rata
1. Rata-Rata Hitung
Rata-rata (mean) adalah ukuran pemusatan lokasi yang
banyak digunakan dalam statistika. Ukuran ini mudah dihitung
dengan memanfaatkan semua data yang dimiliki. Namun demikian,
kekurangan dari ukuran pemusatan rata-rata ini sangat dipengaruhi
nilai ekstrim.
2. Rata-Rata Sementara
Rata-rata hitung ͞x yang diperoleh dari jumlah rata-rata sementara
dan simpangan rata-rata dirumuskan:
3. Rata-Rata Tertimbang

11. 4. Rata-Rata Gabungan
5. Rata-Rata Geometrik
Rata-rata geometric bagi nilai n bilangan positif X1, X2,…, Xn,
adalah akar pangkat n dari hasil kali semua bilangan itu. Jadi :
6. Rata-Rata Harmonik
Rata-rata harmonik bagi nilai n bilangan positif X1, X2,..., Xn,
adalah n dibagi dengan jumlah kebalikan bilangan-bilangan itu.
Jadi :

12. Median
Data statistik yang berada di tengah-tengah disebut median
(Med). Bila banyaknya pengamatan data ganjil, data yang di tengah-
tengah adalah mediannya atau bila banyaknya pengamatan genap, rata-
rata kedua pengamatan yang di tengah adalah mediannya. Median selalu
ditentukan dengan membagi kumpulan data menjadi dua bagian fraksi
yang sama. .
Bila datanya berkelompok atau disusun dalam kelas-kelas
selang, maka rumus mediannya dihitung dengan cara interpolasi.
1. Kuartil
untuk menentukan kuartil pertama, kuartil kedua dan kuartil ketiga
perlu dilakukan interpolasi agar hasilnya lebih cermat.

13. 2. Desil
Desil adalah nilai-nilai yang membagi sekelompok data
pengamatan menjadi 10 bagian yang sama. Dalam ilmu statistic,
desil sering dituliskan sebagai D1, D2,…, D8 dan D9 yang
mempunyai sifat bahwa 10% data jatuh di bawah D1, 20% data
jatuh di bawah D2,… dan 90% data jatuh dibawah D9.
3. Persentil
Persentil adalah nilai-nilai yang membagi sekelompok data
pengamatan menjadi 100 bagian yang sama yang disebut
persentil. Persentil sering disimbolkan sebagai P1, P2,…, P98 dan P99
yang mempunyai sifat bahwa 1% data jatuh di bawah P1, 2% data
jatuh di bawah P2,… dan 99% data jatuh di bawah P99.

14. Modus
Sekumpulan pengamatan data yang nilai terjadinya sering
muncul atau yang mempunyai frekuensi paling tinggi disebut modus (Mo,
atau nilai yang paling banyak di dalam satu kelompok nilai.
Apabila data dikelompokkan dalam kelas-kelas selang dan
disajikan dalam tabel-tabel frekuensi tertentu, maka dalam mencari
modus dapat dipergunakan rumus sebagai berikut:

15. 2. Ukuran Keragaman
UKURAN DATA STATISTIK
Ada beberapa macam ukuran keragaman atau dispense, misalnya
nilai jarak, rata-rata simpangan, simpangan baku, dan koefisien
variasi.
Nilai
Jangkauan
Simpangan
Rata-Rata
Ragam dan
Simpangan Baku

16. 3. Koefisien Variasi
UKURAN DATA STATISTIK
Metode koefisien variasi (coefficient of variation, CV) yaitu simpangan
baku yang dinormalisir: dihitung dari simpangan baku dibagi dengan rata-
rata atau tingkat pengembalian yang diharapkan. Bila simpangan baku
mempunyai satuan mengikuti satuan data asalnya, maka koefisien
variasi tidak mempunyai satuan. Secara matematis rumus koefisien
variasi dinyatakan dalam formulasi berikut ini: