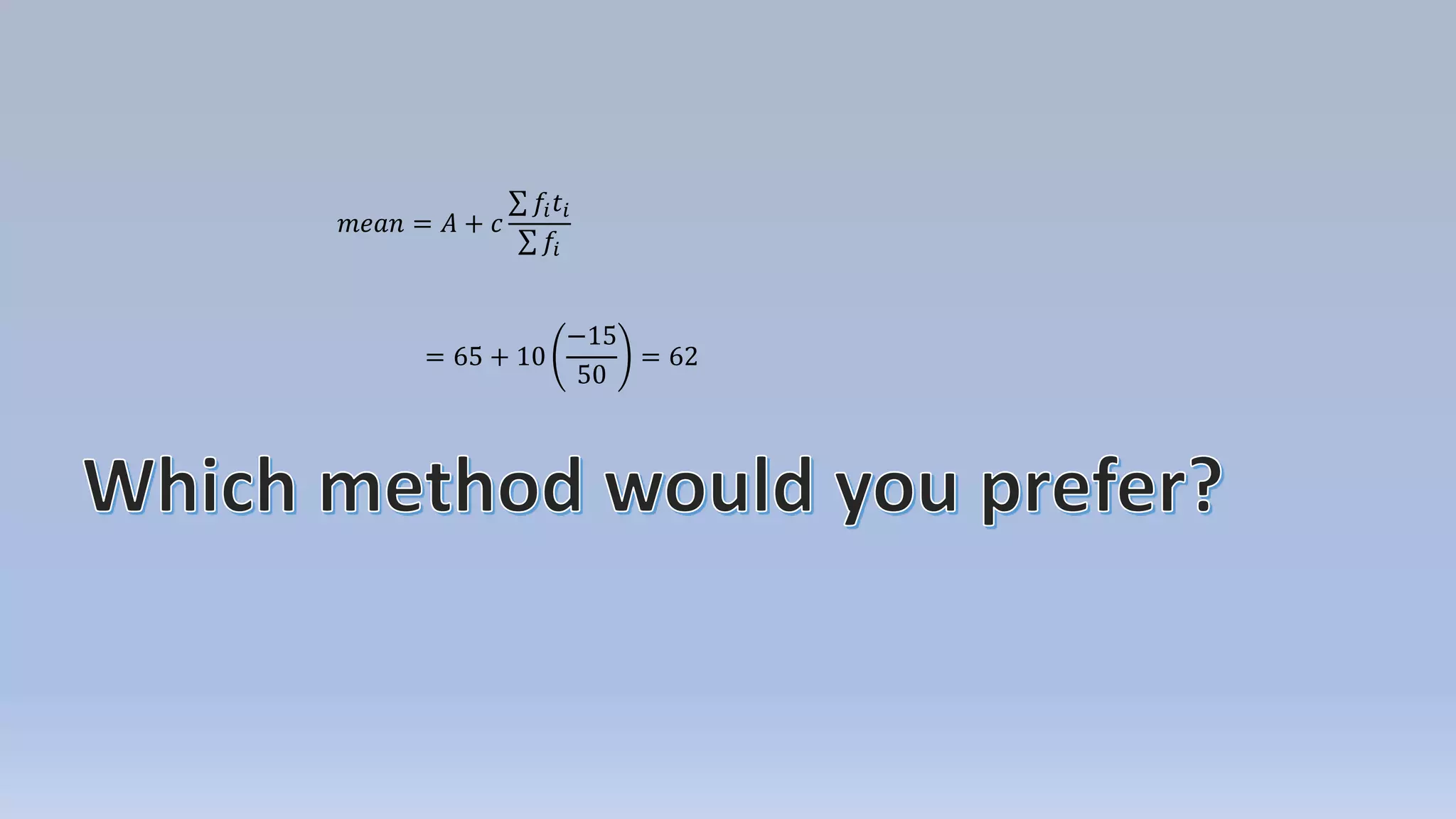The document provides a comprehensive overview of standard deviation calculations using various methods including direct, short-cut, and step deviation. It includes step-by-step examples and formulas to find the mean and standard deviation for given datasets. Statistics concepts are aimed at grade 11 and college-level students, emphasizing the importance of standard deviation as a measure of data dispersion.

1. STANDARD DEVIATION
SUMAN MATHEWS
GRADE 11 MATH
COLLEGE MATH
STATISTICS
𝜎

2. EXPERIENCE:
PREVIEW:
WE DISCUSS THE DIRECT METHOD, SHORT CUT METHOD AND STEP DEVIATION METHOD
TO CALCULATE STANDARD DEVIATION.
ALL THE 3 TYPES OF PROBLEMS ARE DISCUSSED WITH FORMULAE . SO TAKE YOUR PAPER AND PEN
AND WORK THROUGH THE VIDEO WITH ME.
BONUS: FORMULAE OF MEAN USING STEP DEVIATION METHOD ALSO GIVEN

3. THE DEGREE TO WHICH NUMERICAL DATA IS SPREAD OVER AN AVERAGE VALUE IS CALLED
DISPERSION OF DATA.
STANDARD DEVIATION IS THE MOST IMP0RTANT MEASURE OF DISPERSION AND IS WIDELY
USED IN MANY STATISTICAL FORMULAE.

4. 𝜎2
=
𝐼=1
𝑛
(𝑥𝑖 − 𝑥)2
𝑛
𝜎2
=
𝑥𝑖
2
𝑛
− 𝑥2
𝑠𝑡𝑎𝑛𝑑𝑎𝑟𝑑 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛 = 𝜎 = 𝑣𝑎𝑟𝑖𝑎𝑛𝑐𝑒

5. Question 1 ( standard deviation)
Find the standard deviation of the following data
6,8, 10, 12, 14, 16, 18,20, 22, 24
x 𝒙 𝟐
6 36
8 64
10 100
12 144
14 196
16 256
18 324
20 400
22 484
24 576
150 2580
𝜎2
=
2580
10
− (15)2
= 258-225=33
𝜎 = 33 = 5.74

6. QUESTION 2
Find the mean and standard deviation for the following data
𝑥𝑖 𝑓𝑖 𝑓𝑖 𝑥𝑖 𝑓𝑖 𝑥𝑖
2
6 2 12 72
10 4 40 400
14 7 98 1372
18 12 216 3888
24 28 192 4608
28 4 112 3136
30 3 90 2700
40 760 16176
𝜎 =
𝑓𝑖 𝑥𝑖
2
𝑓𝑖
− (
𝑓𝑖 𝑥𝑖
𝑓𝑖
)2
=
16176
40
− (
760
40
)2
For a frequency distribution,
𝜎 =
𝑓𝑖(𝑥𝑖 − 𝑥)2
𝑓𝑖
Direct method

7. = 404.4 − 192
= 43.4 = 6.59𝜎
𝑥 =
𝑓𝑖 𝑥𝑖
𝑓𝑖
= 19

8. Question 3
Find the standard deviation for the following
Class
interval
25-35 35-45 45-55 55-65 65-75
frequency 64 132 153 140 51
We take the midpoint of the class interval as the x values
We use the short cut method.
Let A be the assumed mean
𝑑𝑖 = 𝑥𝑖 − 𝐴
Statistics- grade 11 and college level

9. 𝜎 =
𝑓𝑖 𝑑𝑖
2
𝑓𝑖
− (
𝑓𝑖 𝑑𝑖
𝑓𝑖
)2
C I f 𝒙𝒊 𝒅𝒊
= 𝒙𝒊 − 𝟓𝟎
𝒇𝒊 𝒅𝒊 𝒇𝒊 𝒅𝒊
𝟐
25-35 64 30 -20 -1280 25600
35-45 132 40 -10 -1320 13200
45-55 153 50 0 0 0
55-65 140 60 10 1400 14000
55-65 51 70 20 1020 20400
540 -180 73200
=
73200
540
− (−
180
540
)2
= 135.55 − 0.111
= 135.44 = 11.64
TAKE A= 50

10. QUESTION 4
Calculate the mean, variance and standard deviation of the following data
using step deviation method
C I 30-40 40-50 50-60 60-70 70-80 80-90 90-100
f 3 7 12 15 8 3 2
𝑝𝑢𝑡 𝑡𝑖 =
𝑥𝑖 − 𝐴
𝑐
A is the assumed mean, c is the width of the class interval

11. C I f 𝒙𝒊
𝒕𝒊 =
𝒙𝒊 − 𝟔𝟓
𝟏𝟎
𝒇𝒊 𝒕𝒊 𝒇𝒊 𝒕𝒊
𝟐
30-40 3 35 -3 -9 27
40-50 7 45 -2 -14 28
50-60 12 55 -1 -12 12
60-70 15 65 0 0 0
70-80 8 75 1 8 8
80-90 3 85 2 6 12
90-100 2 95 3 6 18
50 -15 105
𝜎 = 𝑐
𝑓𝑖 𝑡𝑖
2
𝑓𝑖
− (
𝑓𝑖 𝑡𝑖
𝑓𝑖
)2
= 10
105
50
− (
−15
50
)2
= 14.18
Variance = 201
Put A = 65

12. 𝑚𝑒𝑎𝑛 = 𝐴 + 𝑐
𝑓𝑖 𝑡𝑖
𝑓𝑖
= 65 + 10
−15
50
= 62

13. For more videos keep checking my playlist