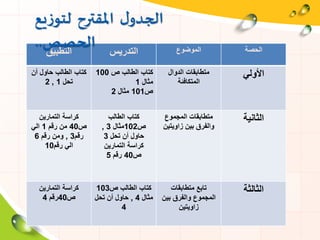
تتناول الوثيقة أهدافًا سلوكية للطلاب في مادة الرياضيات، تركز على متطابقات الدوال المثلثية وقوانين الجمع والفرق. يتضمن المحتوى تدريبات على استخدام النسب المثلثية وشرح مفصل لمتطابقة فيثاغورس. كما تسلط الضوء على تقنيات التعليم الحديثة مثل استخدام الأجهزة اللوحية والوسائل التعليمية المختلفة.

1. L/O/G/O
‫ق‬‫والفر‬ ‫املجموع‬ ‫متطابقات‬
um and difference identities
‫الثانوية‬ ‫قرطبة‬ ‫سة‬‫ر‬‫مد‬/‫بنات‬
‫الرياضيات‬ ‫قسم‬
‫علمي‬ ‫عشر‬‫الحادي‬ ‫للصف‬ ‫عمل‬‫شة‬‫ر‬‫و‬
‫الثاني‬ ‫ي‬ ‫اس‬‫ر‬‫الد‬‫الفصل‬
‫بند‬(9–4)
‫القسم‬ ‫ئيسة‬‫ر‬/‫أ‬.‫العداوني‬‫منيرة‬
‫سة‬‫ر‬‫املد‬‫مديرة‬/‫أ‬.‫املير‬ ‫خالدة‬
‫الفني‬ ‫املوجه‬/‫أ‬.‫الدين‬ ‫ر‬‫نو‬ ‫عبدالوهاب‬
‫األولى‬ ‫املوجهة‬/‫أ‬.‫العلي‬ ‫حصة‬

2. ‫السلوكية‬ ‫األهداف‬..
‫أن‬ ‫علي‬‫قادر‬‫الطالب‬ ‫ن‬‫يكو‬ ‫أن‬ ‫يتوقع‬‫البند‬‫نهاية‬ ‫في‬:
1)‫املتكافئة‬‫الدوال‬‫متطابقات‬ ‫يذكر‬.
2)‫املتكافئة‬‫الدوال‬‫متطابقات‬ ‫باستخدام‬‫املتطابقات‬ ‫بعض‬‫صحة‬ ‫يثبت‬.
3)‫اويتين‬‫ز‬ ‫ملجموع‬‫التمام‬ ‫جيب‬‫ن‬‫قانو‬ ‫يستنتج‬.
4)‫اويتين‬‫ز‬ ‫بين‬ ‫ق‬‫للفر‬‫التمام‬ ‫جيب‬ ‫ن‬‫قانو‬ ‫يستنتج‬.
5)‫اويتين‬‫ز‬ ‫ملجموع‬ ‫الجيب‬‫ن‬‫قانو‬ ‫يستنتج‬.
6)‫اويتين‬‫ز‬ ‫بين‬ ‫ق‬‫للفر‬ ‫الجيب‬‫ن‬‫قانو‬ ‫يستنتج‬.

3. 7)‫اويتين‬‫ز‬ ‫ملجموع‬ ‫الظل‬‫ن‬‫قانو‬ ‫يستنتج‬.
8)‫اويتين‬‫ز‬ ‫بين‬ ‫ق‬‫للفر‬ ‫الظل‬‫ن‬‫قانو‬ ‫يستنتج‬.
9)‫الخاصة‬‫ايا‬‫و‬‫للز‬‫املثلثية‬ ‫النسب‬ ‫يذكر‬.
10)‫ايا‬‫و‬‫الز‬‫لبعض‬‫املثلثية‬ ‫النسب‬‫اآللة‬ ‫استخدام‬ ‫ن‬‫بدو‬ ‫يوجد‬.
11)‫ث‬‫ر‬‫فيثاغو‬‫متطابقة‬ ‫يذكر‬.
12)‫اوية‬‫ز‬‫لل‬‫املثلثية‬ ‫النسب‬ ‫إيجاد‬ ‫في‬‫ث‬‫ر‬‫فيثاغو‬ ‫متطابقة‬ ‫يستخدم‬.
13)‫اويتين‬‫ز‬ ‫ملجموع‬ ‫املثلثية‬ ‫النسب‬ ‫إليجاد‬‫املتطابقات‬ ‫قوانين‬ ‫يستخدم‬.
14)‫اويتي‬‫ز‬ ‫بين‬ ‫ق‬‫للفر‬ ‫املثلثية‬ ‫النسب‬ ‫إليجاد‬‫املتطابقات‬ ‫قوانين‬ ‫يستخدم‬‫ن‬.

4. ‫التعليمية‬ ‫الوسائل‬..
‫جهاز‬‫اآليباد‬.
‫بطاقات‬.
‫الوحدة‬ ‫دائرة‬ ‫لوحة‬.
Mulit mouses
‫ة‬‫ر‬‫سبو‬ ‫أقالم‬

5. ‫الجديدة‬ ‫واملفاهيم‬ ‫املفردات‬..
*‫اويتين‬‫ز‬ ‫مجموع‬ ‫جيب‬
*‫اويتين‬‫ز‬ ‫بين‬ ‫ق‬‫الفر‬ ‫جيب‬
*‫اويتين‬‫ز‬‫مجموع‬ ‫تمام‬ ‫جيب‬
*‫اويتين‬‫ز‬ ‫بين‬ ‫ق‬‫الفر‬ ‫تمام‬ ‫جيب‬
*‫متكافئة‬ ‫دوال‬

6. ‫التطبيق‬ ‫التدريس‬ ‫الموضوع‬ ‫الحصة‬
‫أن‬ ‫حاول‬ ‫الطالب‬ ‫كتاب‬
‫تحل‬1,2
‫ص‬ ‫الطالب‬ ‫كتاب‬100
‫مثال‬1
‫ص‬101‫مثال‬2
‫متطابقات‬‫الدوال‬
‫المتكافئة‬
‫األولي‬
‫التمارين‬ ‫كراسة‬
‫ص‬40‫رقم‬ ‫من‬1‫الي‬
‫رقم‬3,‫رقم‬ ‫ومن‬6
‫رقم‬ ‫الي‬10
‫الطالب‬ ‫كتاب‬
‫ص‬102‫مثال‬3,
‫تحل‬ ‫أن‬ ‫حاول‬3
‫كراسة‬‫التمارين‬
‫ص‬40‫رقم‬5
‫المجموع‬ ‫متطابقات‬
‫بين‬ ‫والفرق‬‫زاويتي‬‫ن‬
‫الثانية‬
‫التمارين‬ ‫كراسة‬
‫ص‬40‫رقم‬4
‫ص‬ ‫الطالب‬ ‫كتاب‬103
‫مثال‬4,‫تحل‬ ‫أن‬ ‫حاول‬
4
‫متطابقات‬ ‫تابع‬
‫بين‬ ‫والفرق‬ ‫المجموع‬
‫زاويتين‬
‫الثالثة‬
‫ل‬‫الجدو‬‫يع‬‫ز‬‫لتو‬ ‫املقترح‬
‫الحصص‬..

7. L/O/G/O
‫األولى‬ ‫الحصة‬

8. ‫التمهيد‬..

9. ‫يس‬‫ر‬‫التد‬..
‫المتكافئة‬ ‫الدوال‬ ‫متطابقات‬
‫األساسية‬ ‫المثلثية‬ ‫الدوال‬ ‫بين‬ ‫المتكافئة‬ ‫الدوال‬ ‫متطابقات‬ ‫تربط‬
‫لها‬ ‫المكافئة‬ ‫والدوال‬
(‫التمام‬ ‫وظل‬ ‫والظل‬ ‫التمام‬ ‫وجيب‬ ‫الجيب‬,‫التمام‬ ‫وقاطع‬ ‫القاطع‬)

10. ‫مثال‬(1..)
sin ( -
𝜋
2
) = - cos  ‫أن‬ ‫أثبت‬:
‫الحل‬..
Sin ( -
𝜋
2
) = sin  - (
𝜋
2
-  )  b – a = - ( a – b )
= - sin (
𝜋
2
-  ) sin (- ) = - sin ( )
= - cos  sin (
𝜋
2
-  ) = cos

11. ‫مثال‬(2..)
cos( -
𝜋
2
) = sin ‫أن‬ ‫أثبت‬:
‫الحل‬..
cos ( -
𝜋
2
) = cos  - (
𝜋
2
-  )  b – a = - ( a – b )
= cos (
𝜋
2
-  ) cos (- ) = cos ( )
= sin  cos(
𝜋
2
-  ) = sin 

12. ‫مثال‬(3..)
Csc ( -
𝜋
2
) = - sec  ‫أن‬ ‫أثبت‬:
‫الحل‬..
csc ( -
𝜋
2
) = csc  - (
𝜋
2
-  )  b – a = - ( a – b )
=
1
𝑠𝑖𝑛−(
𝜋
2
−𝜃)
=
1
−sin (
𝜋
2
−𝜃)
sin ( -  ) = - sin 
=
−1
𝑐𝑠𝑐𝜃
= - sec  sin (
𝜋
2
-  ) = cos 

13. ‫مثال‬(4..)
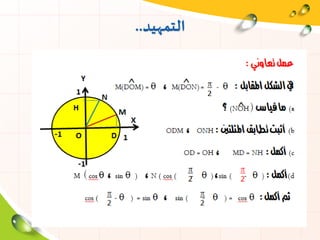
sec ( -
𝜋
2
) = csc  ‫أن‬ ‫أثبت‬:
‫الحل‬..
sec( -
𝜋
2
) =
sec  - (
𝜋
2
-  )  = b – a = - ( a – b )
1
cos[−
𝜋
2
−𝜃 ]
=
=
1
cos(
𝜋
2
−𝜃 )
cos( -  ) = cos 
=
1
𝑠𝑖𝑛𝜃
= csc  cos (
𝜋
2
-  ) = sin 

14. L/O/G/O
‫الثانية‬ ‫الحصة‬

15. ‫السلوكية‬ ‫األهداف‬..‫من‬3-10
‫س‬‫ر‬‫الد‬ ‫تمهيد‬..
‫صفريين‬‫غير‬ ‫ملتجهين‬ ‫الداخلي‬ ‫الضرب‬ ‫ناتج‬‫أن‬ ‫تعلمت‬
𝐴= < XA,YA > ,𝐵 =<XB ,YB>
‫إيجاده‬ ‫يمكن‬‫بإحدى‬‫التاليتين‬ ‫العالقتين‬:
𝐴∙ 𝐵 = XAXB + YAYB
𝐴∙ 𝐵 =॥ 𝐴॥∙॥ 𝐵॥cosθ
‫حيث‬θ‫باملتجهين‬ ‫املحددة‬ ‫اوية‬‫ز‬‫ال‬‫هي‬.

16. ‫يس‬‫ر‬‫التد‬..
‫متطابقة‬ ‫إليجاد‬ ‫ملتجهين‬ ‫الداخلي‬‫الضرب‬ ‫نستخدم‬ ‫سوف‬
cos (α – β)
𝑂𝑁 ∙ 𝑂𝑁 = <cosβ ,sinβ >∙<cosα , sinα > = cosβcosα+sinβsinα …(1)
𝑂𝑁 ∙ 𝑂𝑁 =॥𝑂𝑁॥∙॥𝑂𝑁॥cos(β –α) =1 × 1 × cos(β –α) =cos(β –α)
𝑂𝑁 ∙ 𝑂𝑁 = cos(β –α) …(2)

17. ‫من‬(1)‫و‬(2):
cos(β –α) = cosβcosα+sinβsinα
‫واليجاد‬cos(β +α)
β +α = β – (- α)
cos( β +α) =cos[ β – (- α)]
=cosβcos(-α)+sinβsin(-α)
=cosβcosα+sinβ(-sinα)
cos( β +α)= cosβcosα-sinβsinα

18. ‫كتابة‬ ‫نستطيع‬sin (β+α)‫الشكل‬ ‫على‬(β+α) ]-cos[
𝜋
2
Sin(β+α) = cos[
𝜋
2
-(β +α) ]
= cos[(
𝜋
2
– β - α ]
= cos[(
𝜋
2
- β) - α ]
=cos(
𝜋
2
- β)cosα + sin (
𝜋
2
- β)sinα
Sin(β + α) =sin β cosα + cosβ sinα
Sin(β-α)= sin[ β+(-α)]
= sin β cos(-α) + cosβ sin(-α)
Sin(β - α) =sin β cosα - cosβ sinα

19. ‫بكتابة‬tan(β + α) =
sin(𝛽+𝛼)
cos(𝛽+𝛼)
‫على‬ ‫نحصل‬..
tan(β + α) =
𝑡𝑎𝑛𝛽+𝑡𝑎𝑛𝛼
1−𝑡𝑎𝑛𝛽𝑡𝑎𝑛𝛼
tan(β - α) =
𝑡𝑎𝑛𝛽−𝑡𝑎𝑛𝛼
1+𝑡𝑎𝑛𝛽𝑡𝑎𝑛𝛼

20. ‫والفرق‬ ‫المجموع‬ ‫متطابقات‬..
cos(β – α) = cosβcosα + sinβsinα
cos( β + α)= cosβcosα - sinβsinα
Sin(β + α) =sin β cosα + cosβ sinα
Sin(β - α) =sin β cosα - cosβ sinα
tan(β + α) =
𝑡𝑎𝑛𝛽+𝑡𝑎𝑛𝛼
1−𝑡𝑎𝑛𝛽 𝑡𝑎𝑛𝛼
tan(β - α) =
𝑡𝑎𝑛𝛽−𝑡𝑎𝑛𝛼
1+𝑡𝑎𝑛𝛽 𝑡𝑎𝑛𝛼

21. ‫األمثلة‬..
‫مثال‬(3)‫ص‬102
‫يلي‬ ‫مما‬ ً‫ال‬‫ك‬ ‫الحاسبة‬ ‫اآللة‬ ‫استخدام‬ ‫دون‬ ‫أوجد‬..
(a) Cos15°
(b) sin105°
(c) tan75°

22. (a)Cos15° =
cos(60° - 45°)=
=cos60°cos45°+sin60°sin45°
=
1
2
×
2
2
+
3
2
×
2
2
=
2
4
+
6
4
=
2+ 6
4

23. (b)sin105°=
sin(60°+45°)=
=sin60°cos45°+cos60°sin4
5°
=
3
2
×
2
2
+
1
2
×
2
2
=
6+ 2
4

24. (c)tan75°=
tan(45°+30°)=
=
𝑡𝑎𝑛45°+𝑡𝑎𝑛30°
1−𝑡𝑎𝑛45°𝑡𝑎𝑛30°
=
1+
1
√3
1−
1
√3
=
3+1
3−1
=2+√3

25. (a)
(b)
(c)
sin15°
cos75°
tan105°

26. (a)sin15°=
sin(60° -45°)
=sin60°cos45°-
cos60°sin45°
=
3
2
×
2
2
−
1
2
×
2
2
=
6−√2
4

27. (b)cos75°=
cos(45°+30°)=
=cos45°cos30°-sin45°sin30°
=
2
2
×
3
2
−
2
2
×
1
2
=
6− 2
4

28. (c)tan105°=
tan(60°+45°)=
=
𝑡𝑎𝑛60°+𝑡𝑎𝑛45°
1−𝑡𝑎𝑛60°𝑡𝑎𝑛45°
=
3+1
1− 3×1
=
3+1
1− 3
×
1+ 3
1+ 3
=
2 3+4
− 2
= −2 − 3

29. L/O/G/O
‫الثالثة‬ ‫الحصة‬

30. ‫السلوكية‬ ‫األهداف‬..‫من‬11-14
‫س‬‫ر‬‫الد‬ ‫تمهيد‬..
ً‫ال‬‫أو‬..‫تمرين‬ ‫مناقشة‬(5)‫و‬(7)‫و‬(8)‫ص‬40‫التمارين‬ ‫كراسة‬ ‫من‬..
‫الزاوية‬ ‫ظل‬ ‫أو‬ ‫تمام‬ ‫جيب‬ ‫أو‬ ‫جيب‬ ‫صورة‬ ‫على‬ ‫المقدار‬ ‫اكتب‬..
(5) sin42°cos17° - cos42°sin17°= sin(42 – 17 )= sin25
(8) cos
𝜋
7
𝑐𝑜𝑠𝑥 + 𝑠𝑖𝑛
𝜋
7
𝑠𝑖𝑛𝑥 = cos
𝜋
7
− 𝑥
(7)
𝑡𝑎𝑛19+𝑡𝑎𝑛47
1−𝑡𝑎𝑛19𝑡𝑎𝑛47
=tan(19+47 )=tan66
ً‫ا‬‫ثاني‬..‫فيثاغورث‬ ‫بمتطابقة‬ ‫الطالبات‬ ‫تذكير‬..
Sin2α +cos2α = 1

31. (a)
(b)
(c)
‫يس‬‫ر‬‫التد‬..
‫مثال‬(4.. )‫إذا‬‫كان‬sin α =
4
5
‫أوجدي‬.. cosβ=
−12
13
, 0 < 𝛽 <
3𝜋
2
, 0 < α <
𝜋
2
sin(α + β )
cos( α – β)
tan( α –β )

32. ً‫ال‬‫أو‬..‫نوجد‬:cosα ,sinβ , tanα ,tanβ
‫فيثاغورث‬ ‫متطابقة‬ ‫باستخدام‬
Sin2α +cos2α = 1
(
4
5
)2+ cos2α = 1
cos2α = 1-
16
25
cos2α =
9
25
0 < α <
𝜋
2
cos α > 0
cosα =
3
5

33. sin2β +cos2β = 1
sin2 β +(
−12
13
)2 =1
sin2β = 1-
144
169
sin2β =
25
169
0 < 𝛽 <
3𝜋
2
sinβ <0
sinβ =
−5
13
tan α =
𝑠𝑖𝑛𝛼
𝑐𝑜𝑠𝛼
=
4
5
3
5
tan α =
4
3

34. (a) sin (α +β ) = 𝑠𝑖𝑛𝛼 𝑐𝑜𝑠𝛽 + 𝑐𝑜𝑠𝛼 𝑠𝑖𝑛𝛽
=
4
5
×
−12
13
+
3
5
×
−5
13
=
−48
65
−
15
65
=
−63
65

35. (b) cos(α – β) = 𝑐𝑜𝑠𝛼𝑐𝑜𝑠𝛽 + 𝑠𝑖𝑛𝛼 𝑠𝑖𝑛𝛽
=
3
5
×
−12
13
+
4
5
×
−5
13
=
−36
65
−
20
65
= -
56
65

36. (c)tan (α –β) =
tan 𝛼−tan 𝛽
1+tan 𝛼 𝑡𝑎𝑛𝛽
=
4
3
−
5
12
1+
4
3
×
5
12
=
33
56

37. ‫تحل‬ ‫أن‬ ‫حاول‬)4.. (
‫المثال‬ ‫من‬ ‫المعطيات‬ ‫باستخدام‬)4(‫يلي‬ ‫مما‬ ً‫ال‬‫ك‬ ‫أوجد‬:
(a)cos(α +β) = cosα cosβ – sinα sinβ
=
3
2
×
−12
13
−
4
5
×
−5
13
= - 1,076

38. (a)tan (α +β )=
𝑡𝑎𝑛𝛼+𝑡𝑎𝑛𝛽
1−𝑡𝑎𝑛𝛼 𝑡𝑎𝑛𝛽
=
4
3
+
5
12
1−
4
3
×
5
12
= 3,93
(a)sin ( β – α ) = sin β cosα – cosβ sinα
=
−5
13
×
3
2
-
−12
13
×
4
5
= 0,161

39. L/O/G/O
Thank You!
www.themegallery.com