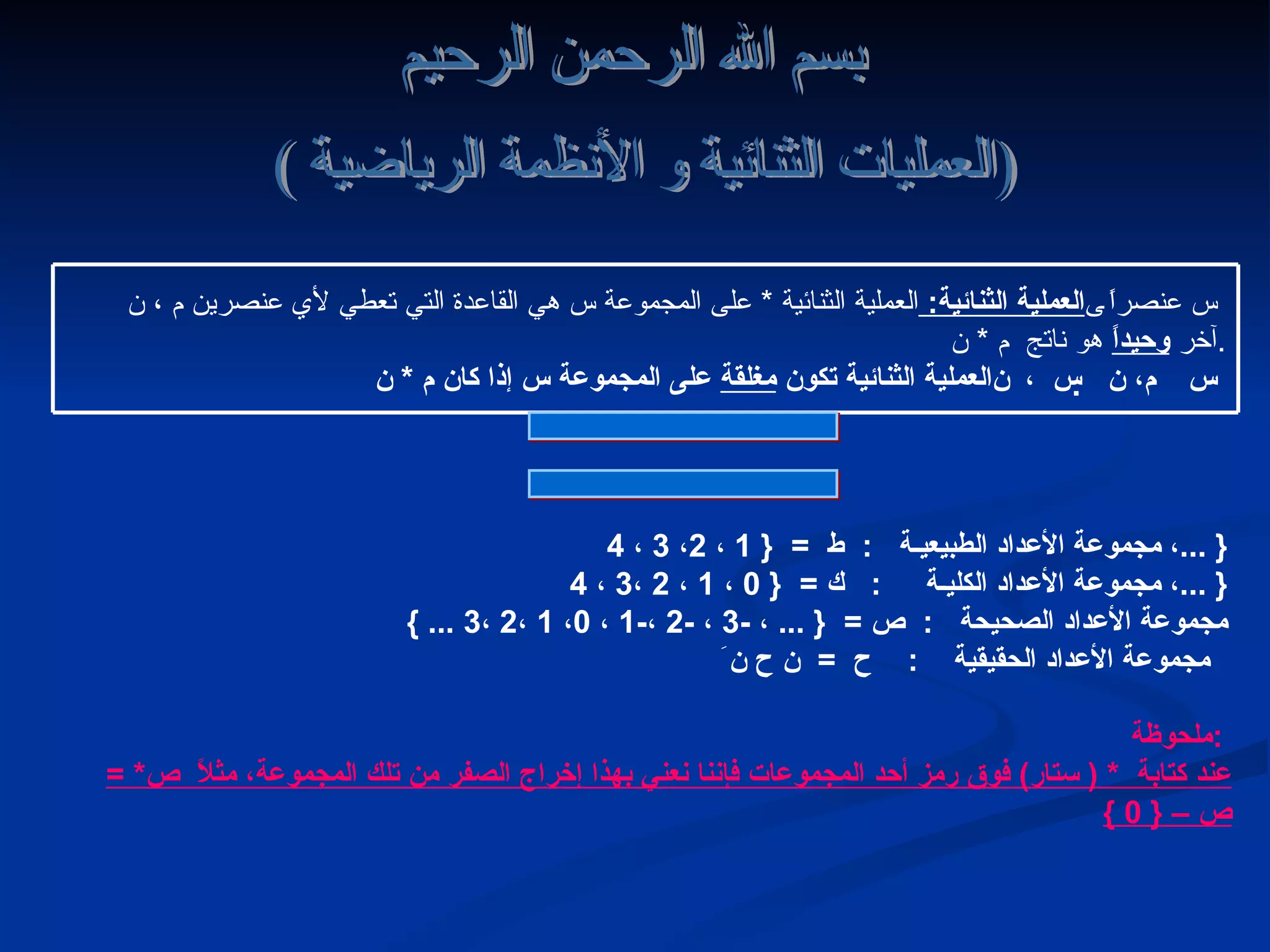
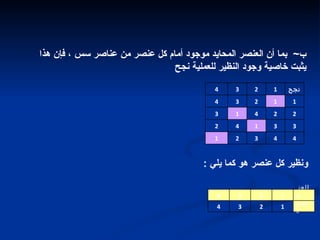
يتناول هذا الوثيقة العمليات الثنائية وأنظمتها الرياضية، مع شرح مفهوم العملية الثنائية والمجموعات المختلفة للأعداد. يتم تحليل العمليات المستخدمة، مثل الجمع والطرح والضرب، وتوضيح خصائصها مثل خاصية الإغلاق والتبديل والتجميع. كما تشمل الوثيقة تمارين لتطبيق المفاهيم الرياضية المذكورة.

1. (العمليات الثنائية و الأنظمة الرياضية ) بسم الله الرحمن الرحيم العملية الثنائية : العملية الثنائية * على المجموعة س هي القاعدة التي تعطي لأي عنصرين م ، ن  س عنصراً آخر وحيداً هو ناتج م * ن . العملية الثنائية تكون مغلقة على المجموعة س إذا كان م * ن  س ،  م، ن  س مجاميع الأعداد : مجموعة الأعداد الطبيعيـة : ط = { 1 ، 2 ، 3 ، 4 ، ... } مجموعة الأعداد الكليـة : ك = { 0 ، 1 ، 2 ، 3 ، 4 ، ... } مجموعة الأعداد الصحيحة : ص = { ... ، -3 ، -2 ، -1 ، 0 ، 1 ، 2 ، 3 ... } مجموعة الأعداد الحقيقية : ح = ن ح ن َ ملحوظة : عند كتابة * ( ستار ) فوق رمز أحد المجموعات فإننا نعني بهذا إخراج الصفر من تلك المجموعة، مثلاً ص * = ص – { 0 } التالي

2. مثال : عملية الجمع عملية ثنائية مغلقة على ط لأن عملية الجمع مغلقة على ط . عملية الضرب عملية ثنائية مغلقة على ط لأن عملية الضرب مغلقة على ط . عملية الطرح ليست عملية ثنائية مغلقة على ط لأن عملية الطرح ليست مغلقة على ط . عملية القسمة ليست عملية ثنائية مغلقة على ط لأن عملية القسمة ليست مغلقة على ط . ملاحظة : إذا كانت العملية الثنائية * معرفة على مجموعة منتهية س أي تحتوي على عدد محدود من العناصر فإننا نكون جدولاً بين النواتج المختلفة لهذه العملية . إذا كانت النواتج جميعها تنتمي لنفس المجموعة المعرفة عليها العملية الثنائية * فإن هذه العملية تكون مغلقة . مجاميع الأعداد التالي

3. تدريبات : أ ) ناقش أي من العمليات الثنائية التالية يمثل عملية ثنائية مغلقة على المجموعة المعرفة عليها : ( ص ، +) ، ( ص ، -) ، ( ص ، × ) ، ( ح ، ÷ ) ، ( ن ، +) ، ( ن ، -) ، ( ح ، × ) ، ( ن ، ÷ ) ب ) بين أي هذه العمليات يمثل عملية ثنائية مغلقة على المجموعة المعرفة عليها وهي طـ : (1) أ * ب = أ + ب -2 (2) أ * ب = 2( أ 2+ ب 2 ) (3) أ  ب = أ + ب -2 ج ) إذا كانت س = { -1 ، 0 ، 1 } ، وكانت  عملية ثنائية معرفة كالتالي : أ * ب = أب على المجموعة س هل تمثل * عملية ثنائية مغلقة ؟ لماذا ؟؟ مجاميع الأعداد التالي

4. خاصية التبديل ملاحظات : 1) إذا وجدنا مثالاً عددياً واحداً لا يحقق الخاصية أ * ب = ب * أ فإن العملية * غير تبديليه . 2) أي عدد من الأمثلة العددية التي تحقق الخاصية أ * ب = ب * أ لا تكفي لإثبات الخاصية التبديلية . 3) إذا كانت المجموعة س مجموعة منتهية فإنه يكفي لإثبات الخاصية التبديلية وجود تماثل حول القطر الرئيسي في جدول العملية المعرفة عليها هذه المجموعة س . التالي خاصية التبديل : لتكن * علمية ثنائية معرفة على المجموعة س . تكون * تبديليه إذا كان أ * ب = ب * أ ،  أ، ب  س

5. تدريبات : بين أي من العمليات الثنائية التالية تبديليه على المجموعات المعرفة إزاء كل منها : (1) أ * ب = أ 2 × ب 2 على ص (2) أ * ب = أ 2+ ب 2+1 على ط (3) أ  ب = أ على س = {2 ، 3 ، 4 ، 5} ( لاحظ أن المجموعة منتهية ولا بد من عمل جدول لها ) مثال : إذا كانت العملية * عملية ثنائية معرفة كالتالي : أ * ب = أ ( أ + ب ) على ص ، هل * تبديليه ؟ الحل : (1) أ * ب = أ ( أ + ب ) = أ 2 + أ ب (2) ب * أ = ب ( ب + أ ) = ب 2 + ب أ من (1) و (2) ينتج أن أ * ب  ب * أ إذاً الخاصية التبديلية غير متحققة على العملية * . خاصية التبديل التالي

6. خاصية التجميع خاصية التجميع : تكون العملية الثنائية  المعرفة على المجموعة س تجميعية إذا كان : ( أ * ب ) * ج = أ * ( ب * ج ) ،  أ، ب، ج  س ملاحظات : 1) لنفي خاصية التجميع عن العملية الثنائية  يكفي وجود مثال عددي واحد لا يحقق الخاصية التجميعه 2) لا يكفي أي عدد من الأمثلة العددية لتحقيق الخاصية التجميعه للعملية الثنائية  وإنما يجب إثبات ذلك رياضياً 3) لكي نثبت خاصية التجميع من جدول عملية يجب أن نتأكد من أن شرط التجميع متحقق لكل اختيار ممكن لثلاثة عناصر من عناصر المجموعة ( ليس بالضرورة أن تكون العناصر مختلفة ) ، لذلك فإن إثبات خاصية التجميع للعمليات المعطاة بجدول تكون دائماً من الأمور المرهقة . 4) يُقبل بدون برهان أن عمليتي الجمع والضرب الساعاتي  ­­ ن ،  ­­ ن على المجموعة صن هما عمليتان تجميعيتان . التالي

7. مثال (2) : هل العملية الثنائية * المعرفة كالتالي تجميعية : أ * ب = أ + ب - أ ب على ص الحل : نفرض أ ، ب ، ج  ص 1 ـ ( أ * ب ) * ج = ( أ ب – 10)  ج = ( أ ب – 10) ج – 10 = أ ب ج – 10 ج – 10 2- أ * ( ب * ج ) = أ * ( ب ج – 10) = أ ( ب ج – 10) - 10= أ ب ج – 10 أ – 10 من (1) و (2) ينتج أن ( أ * ب ) * ج  أ * ( ب * ج ) مثال (1) : هل العملية الثنائية * المعرفة كالتالي : س * ص = س ص – 10 على ح عملية ثنائية تجميعية ؟؟ الحل : نفرض أ ، ب ، ج  ح 1) ( أ * ب ) * ج = ( أ ب – 10)  ج = ( أ ب – 10) ج – 10 = أ ب ج – 10 ج – 10 2) أ * ( ب * ج ) = أ * ( ب ج – 10) = أ ( ب ج – 10) - 10= أ ب ج – 10 أ – 10 من (1) و (2) ينتج أن ( أ * ب ) * ج  أ * ( ب * ج ) إذاً العملية الثنائية * عملية غير تجميعية . خاصية التجميع التالي

8. تدريبات : بين أي من العمليات الثنائية التالية هي عملية تجميعية على المجموعة المعرفة عليها كل منها : س * ص = س + 1 على ط س * ص = أ + ب + 5 على ن س  ص = س 2 + ص 2 على ح س  ص = ( س – ص )2 على ن خاصية التجميع التالي

9. 1_ لإيجاد العنصر المحايد و رمزه ( ه ) نحل ( ا * ه = أ ). 2_ لإيجاد نظير العنصر ( أ ) و يرمز له (- أ ) نحل ( أ * - أ = ه ). 3_ لإيجاد النظير يجب أيجاد العنصر المحايد أولاً . كما انه في عملية الجمع على الأعداد الصحيحة نلاحظ انه لكل عدد صحيح أ يوجد عدد صحيح (– أ ) بحيث أن أ + - أ =  ( العنصر المحايد ) , العنصر - أ يسمى نظير العنصر أ . العنصر المحايد والنظير العنصر المحايد و النظير : لتكن * عملية ثنائية معرفة على المجموعة س يكون العنصره  س محايد اذا و فقط اذا كان أ * ه  أ ,  أ  س . أي انه  أ  س , ه عنصر محايد  أ * ه = ه * أ = أ ملاحظات : التالي

10. مثال : العدد 2 نظيره هو العدد -2 بحيث ان 2+- 2 =-2+2 =  العدد -5 نظيره هو العدد 5 بحيث ان -5 +5 = 5+-5 =  و كذلك في عملية الضرب على الأعداد النسبية عدا الصفر , لاحظ انه لكل عدد نسبي أ يوجد عدد نسبي 1  أ بحيث ان أ  1  أ =1 ( العنصر المحايد ) , العنصر 1  أ يسمى نظير العنصر أ و هذا يقودنا للتعريف التالي : العنصر المحايد والنظير تعريف : لتكن * عملية ثنائية معرفة على المجموعة س , ليكن ه هو العنصر المحايد . يسمى العنصر ب هو نظير العنصر أ بالنسبة للعملية الثنائية * اذا تحقق الشرط التالي : أ * ب ب * أ = ه و سوف نرمز لنظير أ بالرمز (- أ ) و يقرا نظير أ التالي

11. امثلة : مثال 1: لتكن * عملية ثنائية معرفة على ط كالتالي : س * ص = س + ص -2 1_ اوجد العنصر المحايد 2_ اوجد نظير كل من العناصر 2 و 7 ان وجدت . الحل :_ 1_ نفرض العنصر المحايد هو ه  س * ه = ه * س = س  س + ه -2= ه + س -2= س  ه =2 2_ نفرض ان نظير س هو –س  س *- س =- س * س = ه  س + - س -2 = - س + س -2=2  - س = 4- س  نظير 2 هو 4 – 2=2 نظير 7 هو 4 -7 =-3 ( مرفوض ) لان -3  ط أي ان العنصر 7 ليس له نظير . العنصر المحايد والنظير التالي

12. مثال 2: لتكن العملية نجح معرفة على المجموعة س = { 1 ، 2 ، 3 ، 4 } ممثلة بالجدول التالي : ا ~ اوجد العنصر المحايد للعملية نجح ب ~ هل خاصية النظير للعملية نجح موجودة ؟ أوجد نظير كل عنصر ( إن أمكن ). الحل ا ~ العنصر المحايد هو ( تقاطع الصف المماثل للصف العلوي مع العمود المماثل للعمود العلوي ) م = 1 العنصر المحايد والنظير التالي 1 2 3 4 4 2 4 1 3 3 3 1 4 2 2 4 3 2 1 1 4 3 2 1 نجح 1 2 3 4 4 2 4 1 3 3 3 1 4 2 2 4 3 2 1 1 4 3 2 1 نجح

13. ب ~ بما أن العنصر المحايد موجود أمام كل عنصر من عناصر سس ، فإن هذا يثبت خاصية وجود النظير للعملية نجح ونظير كل عنصر هو كما يلي : العنصر المحايد والنظير السابق 1 2 3 4 4 2 4 1 3 3 3 1 4 2 2 4 3 2 1 1 4 3 2 1 نجح 4 3 2 1 نظيره 4 3 2 1 العنصر

14. تم بحمد الله ورعايته بأشراف الاستاذ الفاضل : أ. احمد عبد القادر عمل الطلاب : 1- صادق متروك 2- طارق علان 3- محمد ابو سعده 4- ليث خالد 5- اسامه عادل