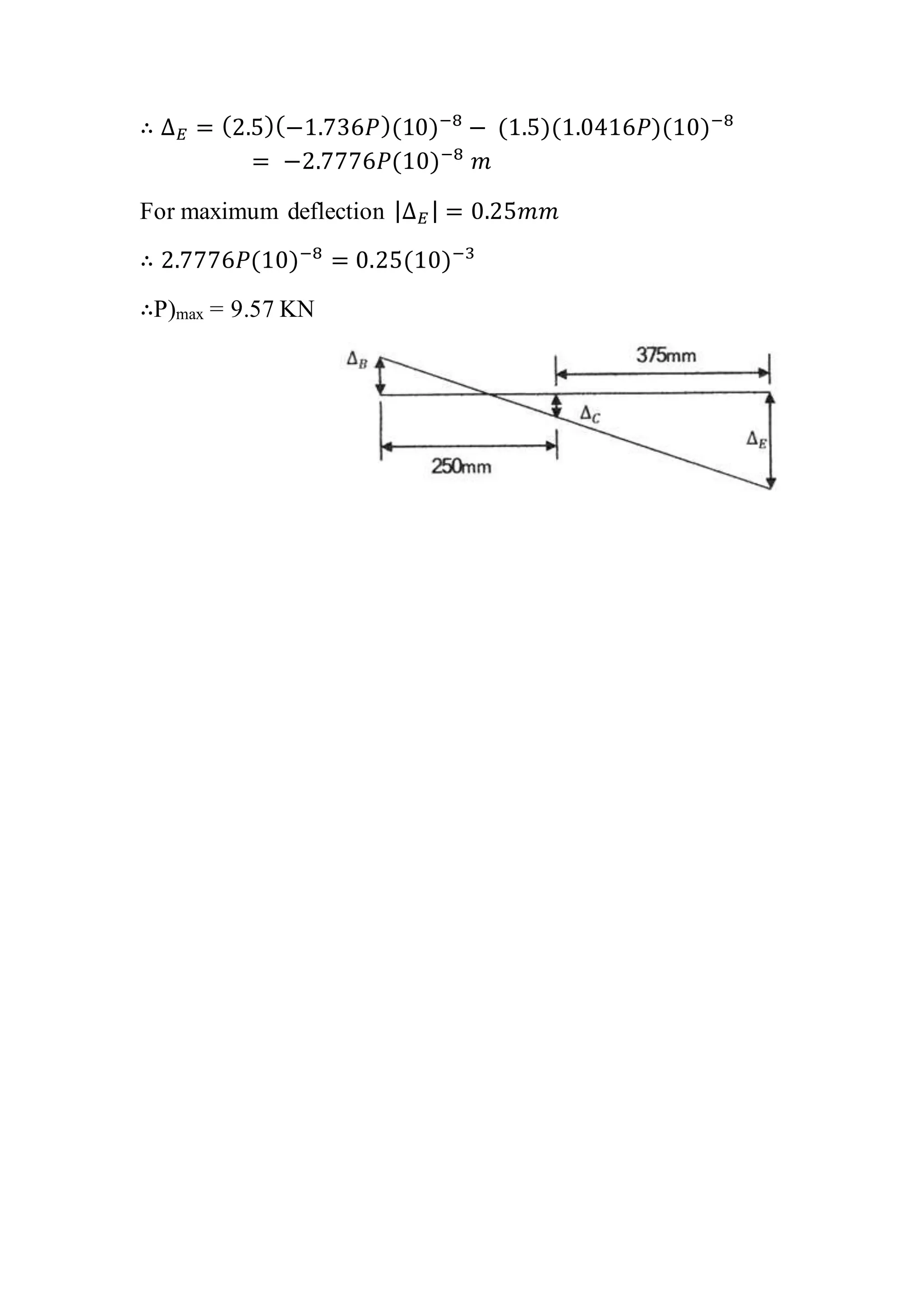
This document contains 6 problems involving calculations of stress, strain, deflection and load capacity for mechanical structures composed of rods, beams, and wires under various loading conditions. The materials involved include steel, aluminum, brass and polystyrene. Deflections, elongations, average stresses and maximum supported loads are calculated using basic mechanics of materials equations relating force, stress, strain, modulus of elasticity and structural geometry.

1. Problem Number (1)
A 3-mm thick hollow polystyrene cylinder E = 3GPa and
a rigid circular plate (only part of which is shown) are used to
support a 250-mm long steel rod AB (E = 200 GPa) of 6-mm
diameter. If a 3.2KB load P is applied at B, determine (a) the
elongation of rod AB, (b) the deflection of point B, (c) the
average normal stress in rod AB.
Solution:
∆𝐿 =
𝐹 × 𝐿
𝐴 × 𝐸
=
3200 × 0.25
3.14 × 9 × 10−6 × 200 × 109
= 1.4 × 10−4
𝑚
Deflection of B =
3200 × 0.03
3.14((25)2 − (22)2) × 10−6 × 3 × 109
+ 1.4 × 10−4
= 0.214 𝑚𝑚
𝜏 =
𝐹
𝐴
=
3200
3.14 ×9 × 10−6 = 113.2 𝑀𝑃𝑎

2. Problem Number (2)
Two solid cylindrical rods are joined at B and loaded as
shown. Rod AB is made of steel E = 200GPa and rod BC of
brass E = 105GPa. Determine (a) the total deformation of the
composite rod ABC, (b) the deflection of point B.
Solution:
Assume that the force 40KN is directed to downward at point B
∆𝐿 =
30 × 103
×0.25
3.14 ×15 ×15 × 10−6 ×200 × 109
+
70 × 103
×0.3
3.14 ×25 ×25 × 10−6 ×105 × 109
= 0.393 𝑚𝑚
Deflection of Point B =
70 × 103 ×0.3
3.14 ×25 ×25 × 10−6 ×105 × 109
=
0.102 mm
Problem Number (3)

3. Both portions of the rod ABC are made of an aluminum
for which E = 70 GPa. Knowing that the magnitude of P is
4KN, determine (a) the value of Q so that the deflection at A is
zero, (b) the corresponding deflection of B.
Solution:
∆𝐿 𝐵𝐶 = ∆𝐿 𝐴𝐵
(𝑄 − 4000) × 0.5
3.14 × 0.03 × 0.03 × 70 × 109
=
4000 × 0.4
3.14 × 0.01 × 0.01 × 70 × 109
Then, Q = 32800 N
Then, Deflection of B =
(32800−4000) ×0.5
3.14 ×0.03 ×0.03 ×70 × 109 =
0.0728 mm
Problem Number (4)

4. The rod ABC is made of an aluminum for which E =
70GPa. Knowing that P = 6KN and Q = 42 KN, determine the
deflection of (a) point A, (b) point B.
Solution:
Deflection of A = ∆𝐿 𝐴𝐵 − ∆𝐿 𝐵𝐶
=
6000 ×0.4
3.14 × 0.01 ×0.01 ×70 × 109
−
(42000−6000) ×0.5
3.14 ×0.03 ×0.03 ×70 × 109
=
0.01819 𝑚𝑚
Deflection of B =
(42000−6000)×0.5
3.14 ×0.03 ×0.03 ×70 × 109
= 0.091 𝑚𝑚
Problem Number (5)

5. Each of the links AB and CD is made of steel
(E = 200GPa) and has a uniform rectangular cross section of
6 * 24 mm. Determine the largest load which can be suspended
from point E if the deflection of E is not to exceed 0.25 mm.
Solution:
∑MB = P(375 + 250) – FDC (250) = 0
∴ 𝐹 𝐷𝐶 = 2.5𝑃 (𝑇𝑒𝑛𝑠𝑖𝑜𝑛)
∑Fy = FDC – FBA – P = 0
∴ 𝐹 𝐵𝐴 = 1.5𝑃 (𝑇𝑒𝑛𝑠𝑖𝑜𝑛)
∴ ΔCD =
𝐹 𝐷𝐶 𝐿 𝐷𝐶
𝐸 𝐷𝐶 𝐴 𝐷𝐶
=
2.5𝑃 (200)(10)−3
(200)(10)9(6)(24)(10)−6
= 1.736𝑃 (10)−8
𝑚 (𝐷𝑜𝑤𝑛𝑤𝑎𝑟𝑑)
∴ ΔBA =
𝐹 𝐵𝐴 𝐿 𝐴𝐵
𝐸𝐴𝐵 𝐴 𝐴𝐵
=
1.5𝑃 (200)(10)−3
(200)(10)9(6)(24)(10)−6
= 1.0416𝑃 (10)−8
𝑚 (𝑈𝑝𝑤𝑎𝑟𝑑)
From geometry of the deflected structure:
∴ Δ 𝐸 = (
250 + 375
250
) ΔC − (
375
250
)ΔB

6. ∴ Δ 𝐸 = (2.5)(−1.736𝑃)(10)−8
− (1.5)(1.0416𝑃)(10)−8
= −2.7776𝑃(10)−8
𝑚
For maximum deflection |Δ 𝐸 | = 0.25𝑚𝑚
∴ 2.7776𝑃(10)−8
= 0.25(10)−3
∴P)max = 9.57 KN

7. Problem Number (6)
The length of the 2-mm diameter steel wire CD has been
adjusted so that with no load applied, a gap of 1.5mm exists
between the end B of the rigid beam ACB and a contact point E.
knowing that E = 200 GPa, determine where a 20-kg block
should be placed on the beam in order to cause contact between
B and E.
Solution: