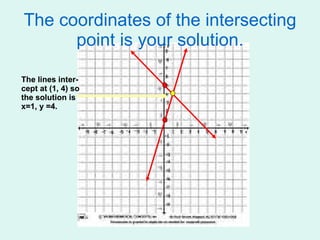
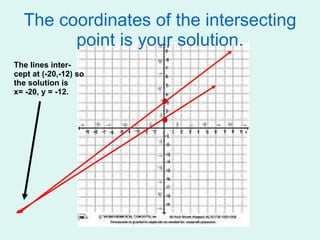
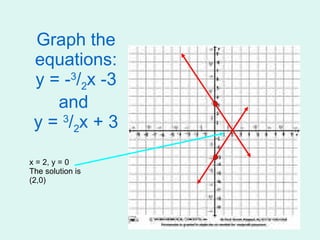
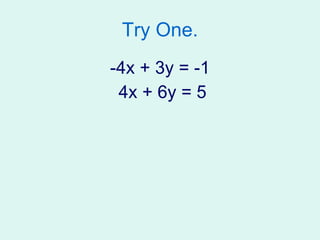This document summarizes three methods for solving systems of linear equations: graphing, substitution, and elimination. It provides examples of solving systems of two equations using each method. Graphing involves plotting the lines defined by each equation on a coordinate plane and finding their point of intersection. Substitution involves isolating a variable in one equation and substituting it into the other equation. Elimination involves adding or subtracting multiples of equations to remove a variable and solve for the remaining variable.

1. Solving Linear Equations Using Graphing Substitution and Elimination Need some homework help? Go to: http://go.hrw.com Keyword: MA1 Homework Help

2. What’s the Deal? There are a number of ways to solve groups of linear equations. In this review, we will find points on a coordinate plane that solve linear equations in standard form and y-intercept form.

3. Three Parts Part One – Solve linear equations by graphing. Part Two – Solve linear equations by substitution. Part Three – Solve linear equations by elimination.

4. Solving for linear equations answers the question: What values of x and y fit into both equations? The answer is usually given in (x,y) format (ie. (-4, 6) or (3,8).

5. Remember - Slope intercept form: y = mx + b m = slope b = y-intercept In y = 1/2x – 7 , the place where the line intercepts the y-axis (called the y-intercept) is negative seven (-7). The slope, which is the rise over the run, is ½ (the fraction before the x): Rise = up, or plus one (+1) Run = right, or plus two (+2).

6. If the slope is ½ Rise Run = slope = m The rise is 1 and the run is 2. From the origin (0,0), go up 1 and right 2.

7. Graphing Systems of equations y = 3x + 1 y = -x + 5 Since both are in y-intercept format (y=mx+b) find the point through which the line intercepts the y-axis. From that point, graph the slope.

8. Graph y=3x + 1 In the following slide, you will see +1 graphed as the y-intercept. And the slope rise =3 and run = 1 will be graphed over the y-intercept.

9. y = x + 1 y-intercept

10. Let’s add y = -x + 5 The slope is -1. Or down one And right one.

11. The coordinates of the intersecting point is your solution. The lines inter- cept at (1, 4) so the solution is x=1, y =4. The lines inter- cept at (1, 4) so the solution is x=1, y =4.

12. Solve by graphing y = x +3 y = x +1 The next two slides will show the solution.

13. The coordinates of the intersecting point is your solution. The lines inter- cept at (-20,-12) so the solution is x= -20, y = -12.

14. Now solve equations in standard form. 3 x + 2y = -6 and -3 x + 2y = 6 When graphing, you must convert equations from standard form to y-intercept form. Let’s review that from a previous lesson using the equations above…

15. Change 3x + 2y = -6 to y-intercept form 3x + 2y = -6 - 3x -3x 2y = -3x - 6 Now we need to get y isolated. In this case, let’s divide both sides by 2. 2y = -3x - 6 2 2 2 Now simplify. y = - x -3 Subtract -3x from both sides

16. Change -3x + 2y = 6 to y-intercept form -3x + 2y = +6 + 3x 3x 2y = 3x + 6 Get y isolated. Divide both sides by 2. 2y = 3x + 6 2 2 2 Now simplify. y = 3 / 2 x + 3 Add 3x to both sides

17. Graph the equations: y = - 3 / 2 x -3 and y = 3 / 2 x + 3 x = 2, y = 0 The solution is (2,0)

18. End of Part One

19. Part Two – Solve linear equations by substitution Need Help? Go online to go.hrw.com See your textbook’s “internet connect” notes

20. Here’s what will happen 1) Find the x or y value that is isolated, such as x = y+3. The x-value is isolated. 2) Insert the isolated value into the equation, this allows you to solve for one variable at a time. 3) Find the value of one variable. 4) Insert that value into either equation and solve for the second variable.

21. Solve for the following equations. 2x + 8y = 1 x = 2y Step one ( listed on the previous slide ) 1) Find the x or y value that is isolated, such as x = 2y. The x-value is isolated. Since x = 2y, you insert 2y wherever x occurs.

22. Step 2) Insert the isolated value into the equation, this allows you to solve for one variable at a time. 2( 2y ) + 8y = 1 4y + 8y = 1 12y=1 12y = 1 12 12 y = 1 / 12 Replace the x with 2y by substitution. Multiply 2*2y. Combine like terms. Divide both sides by 12 Solve for y. Careful! You are only half done. You still have to solve for the other variable!

23. Solve for: 2x + 8y = 1 and x = 2y 3) Find the value one variable. This was done on the previous slide. y = 1 / 12 4) Insert that value into either equation and solve for the second variable. x = 2 ( ) or x = (which is in lowest terms) The solution is (1/6, 1/12)

24. Try one. 2x + y = 5 x = 7

25. x is given as 7. Insert 7 for any occurrence of x to solve for y. First solve for y. 2x + y = 5 2(7) + y = 5 14 + y = 5 -14 -14 y = -9 Since you know that x = 7 and y = -9, insert those values into a coordinate in (x,y) format. Solution: ( 7, -9 )

26. Solve for x and y. 3x + y = 4 and 5x – 7y = 11 Notice that y can more easily be isolated in the first equation. The Plan: Let’s isolate y. Then we will use the value for y to substitute for y.

27. Subtract 3x from both sides to isolate y. 3x + y = 4 - 3x -3x y = -3x +4 5x – 7y = 11 5x – 7( -3x +4) = 11 Now that we know that y = -3x+4, substitute. Which property gets used next?

28. The Distributive Property is used. 5x – 7( -3x +4) = 11 5x +21x -28 = 11 26x – 28 = 11 +28 +28 Distribute -7 to both terms inside the parentheses. -7(-3x) = + 21x -7(4) = -28 Combine like terms. Add 28 to both sides. Next: divide both sides by 26.

29. Continuing… 26x = 39 26 = 26 x = 39 / 26 x = 3 / 2 3( 3 / 2 ) + y = 4 Find lowest terms (divide 39 and 26 by the LCM) Using the x value, solve for y in one of the equations.

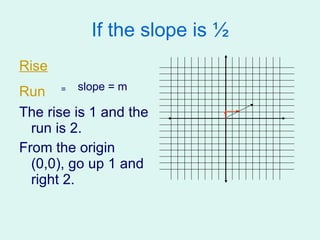
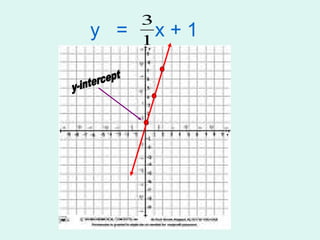
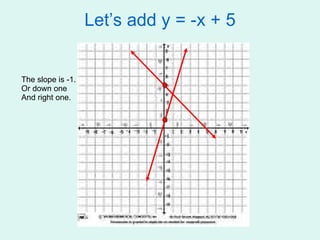
30. 3( 3 / 2 ) + y = 4 3 x 3 + y = 4 1 x 2 9 / 2 + y = 4 - 9 / 2 -4 ½ y = -½ ( 3 / 2 , -½) or (1.5, -0.5) Change 3 to a fraction Multiply the fractions Subtract 9 / 2 [ or 4 ½] from both sides. The solutions in fraction and decimal forms.

31. Part Three – Solving equations by Elimination Need some homework help? Go to: http:// go.hrw.com Keyword: MA1 Homework Help

32. Solve using substitution after manipulating equations in standard form. 2x + 3y = 21 -3x – 3y = -12 Which value, x or y, should we work with first? This looks like a very long, drawn-out problem. Is there a better way?

33. Let’s solve by elimination. This method uses opposites to eliminate one of the variables. Which variable should be eliminated? 2x + 3y = 21 -3x – 3y = -12

34. 2x + 3y = 21 -3x – 3y = -12 Notice that the coefficients with the y value are opposites. (+3 and -3). If we combine these two equations together in columns, we can eliminate the y values. We will solve for x and then insert it’s value into one of the original equations to solve for y.

35. The steps and explanations 2x + 3y = 21 -3x – 3y = -12 -1x + 0 = 9 -1x + 0= 9 -1 -1 x = -9 Add terms from top to bottom. +2x - 3x +3y - 3y Divide both sides by -1 . Now go back and insert -9 for x.

36. 2x + 3y = 21 -3x – 3y = -12 You may pick either one. 2(-9) + 3y = 21 -18 + 3y = 21 (add 18 to both sides) +3y = 39 3 3 y = 13 Solution (-9, 13) -3(-9) – 3y = -12 +27 – 3y = -12 (subtract 27 from both sides) -3y = -39 -3 -3 y = 13

37. Try One. -4x + 3y = -1 4x + 6y = 5

38. Eliminate the x values. -4x + 3y = -1 4x + 6y = 5 9y = 4 9y = 4 9 9 y = 4 / 9 Solve for x. 4x + 6( 4 / 9 ) = 5 4x + 24 / 9 = 45 / 9 Subtract 21 / 9 from both sides. 4x = 2 1 / 3 Go to the next slide…

39. 4x = 21 / 9 Divide both sided by 4. 4x = 21 / 9 4 4 X = X = To divide fractions, multiply by the reciprocal

40. Ready to go one more step? What if you don’t have an easy choice. You may find that neither equation has opposite coefficients.

41. Let’s try 11x + 2y = -8 and 8x + 3y = 5 Our goal is to eliminate a variable using opposite coefficients. It looks like we should use 2y and 3y since they are smaller numbers. If we multiply both sides of the top equation by -3 and both sides of the bottom by 2, we should get coefficients of 6 and -6.

42. Multiply both sides (11x + 2y) = (-8) (8x + 3y) = (5) -3(11x + 2y) = (-8)-3 2(8x + 3y) = (5)2 We’ll put all four values into parentheses. Multiply both sides of the top by -3 Multiply both sides of the second equation by 2.

43. Results of the First Steps -3(11x + 2y) = (-8)-3 2(8x + 3y) = (5)2 ----------------------- -33x – 6y = +24 16x + 6y = +10 -17x + 0 = 34 From the previous slide Use the distributive property Now eliminate

44. -17x = 34, x = -2 11x + 2y = -8 11(-2) + 2y = -8 -22+ 2y = -8 2y = 14 y = 7 Pick one of the original equations. Solve for the other variable. Add 22 to both sides. -8 +22 = 14. Solution (-2, 7)

45. One more for practice 3x - 2y = 2 4x – 7y = 33 -------------------- -4(3x - 2y) = (2)-4 3(4x – 7y) = (33)3 ------------------------- Solution on the next slide…

46. One more for practice 3x - 2y = 2 4x – 7y = 33 -------------------- -4(3x - 2y) = (2)-4 3(4x – 7y) = (33)3 ------------------------- -12x + 8y = -8 12x – 21y = 99 ----------------------- -13y = 91 -13y = 91 -13 -13 y= -7 --------------------------- 3x-2(-7)= 2 3x + 14 = 2 3x = -12 x= -4 ------------- Solution (-4, -7)

47. Which way of solving works best for you? Graphing? Substitution? Elimination? Make sure you know them all in order to pick the best way to solve each problem.

48. You have reviewed the first three parts of Chapter 7.