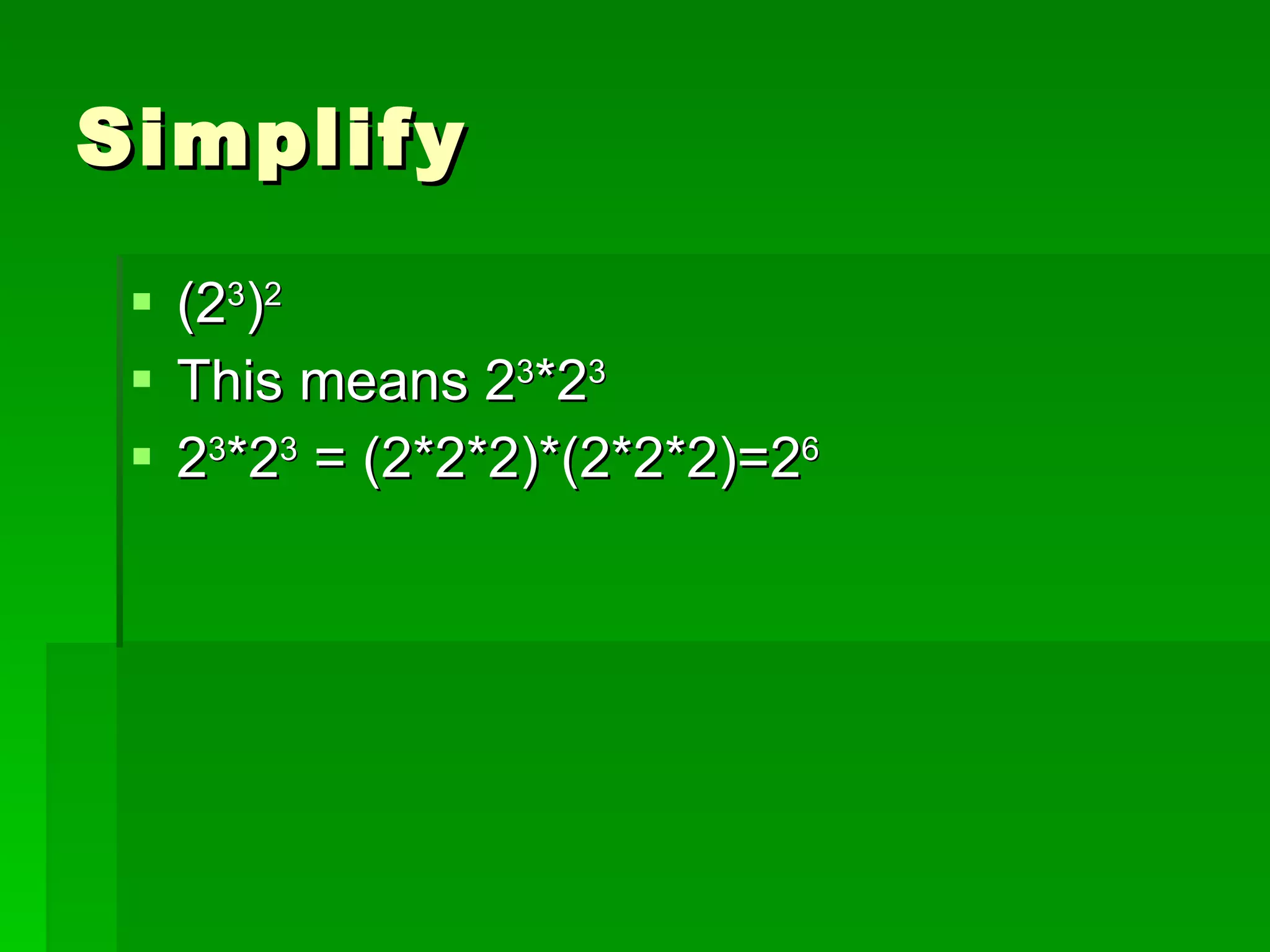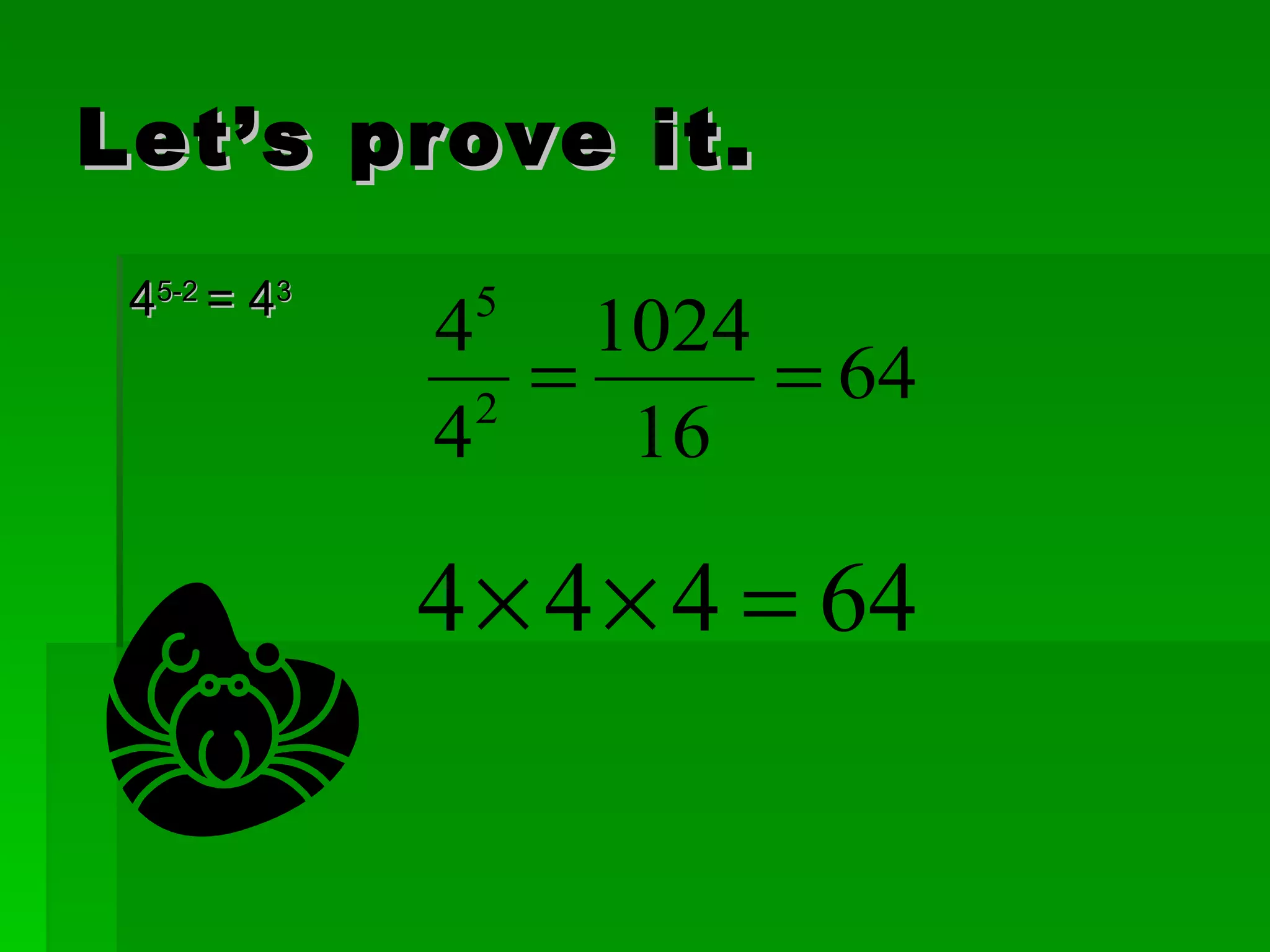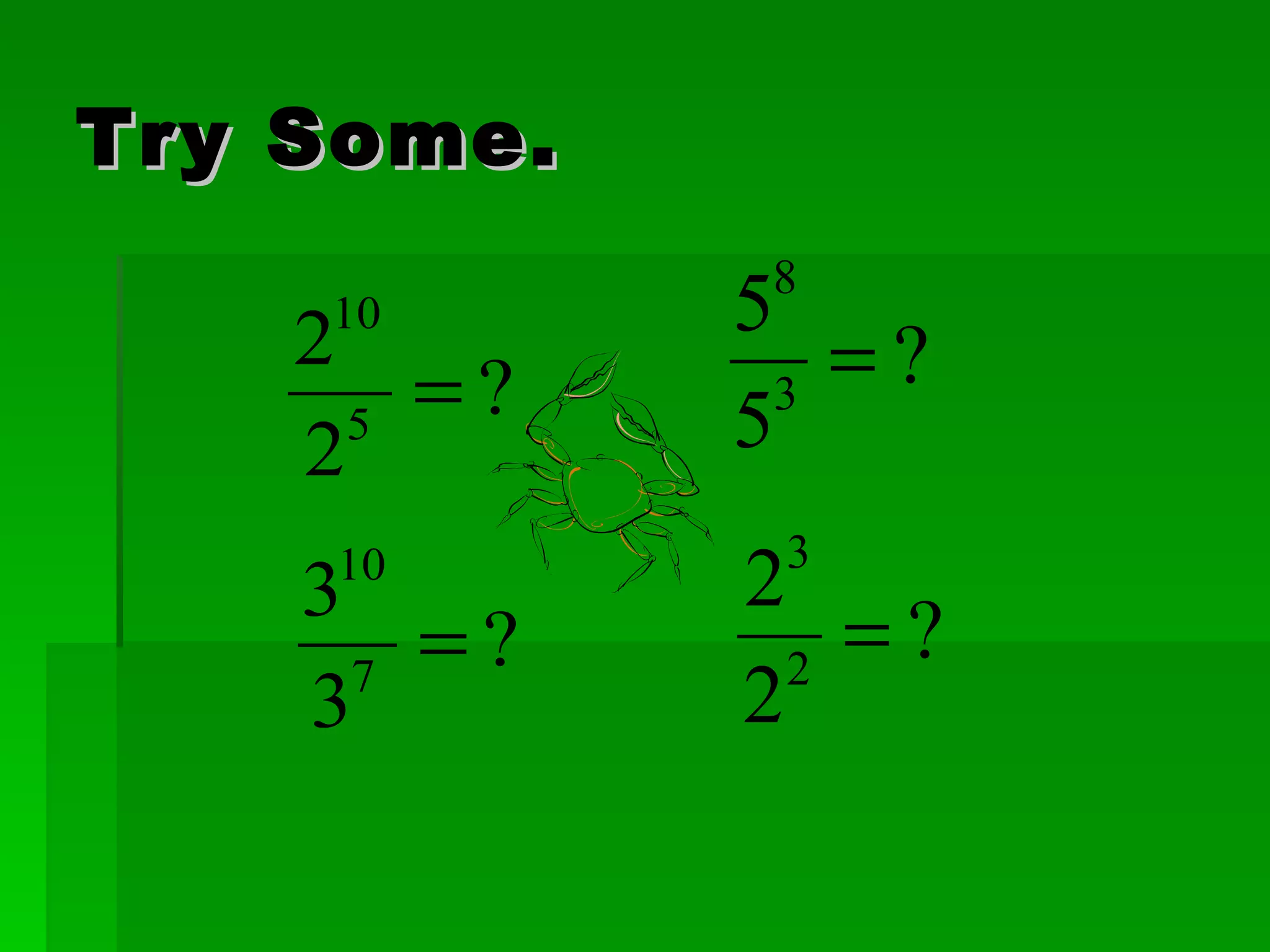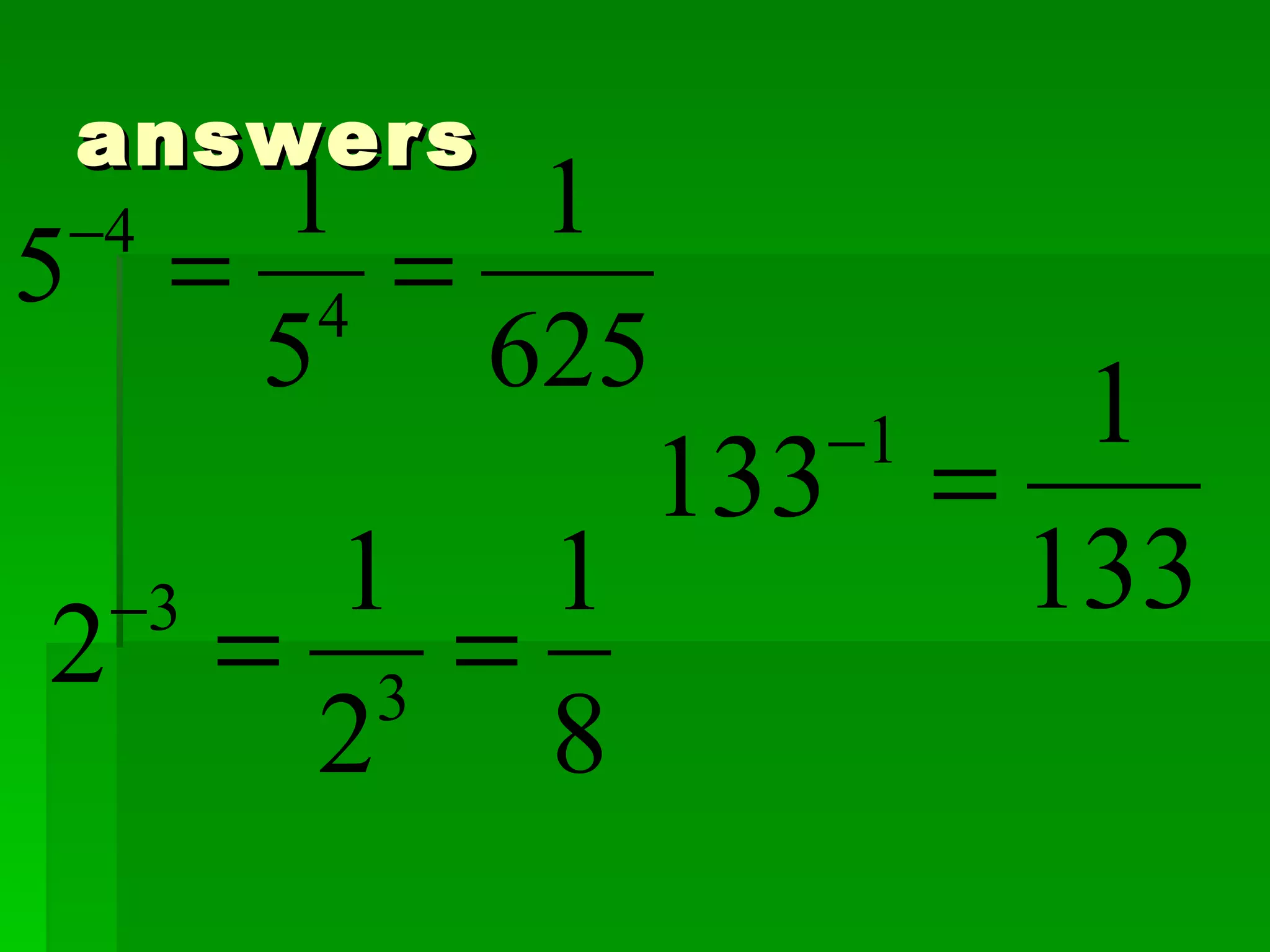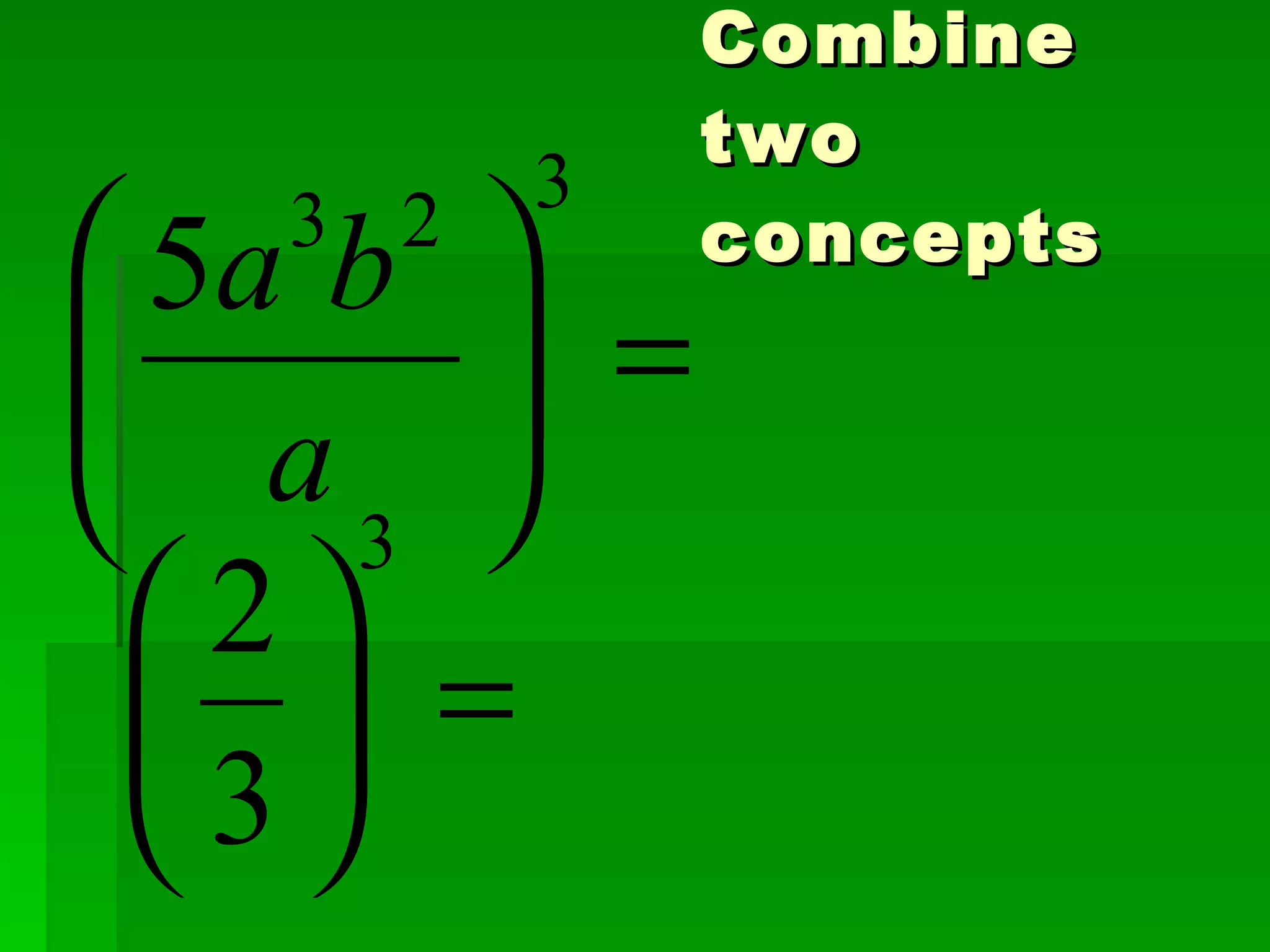The document discusses exponents and properties related to exponents. It introduces the power of powers property, which states that when a number is raised to a power that is then raised to another power, you multiply the exponents. For example, (3^3)^4 = 3^(3×4) = 3^12. It also discusses how to simplify expressions with negative exponents by writing them as fractions with positive exponents.

1. Power of a Power Finding powers of numbers with exponents (x m ) n = x mn

2. Simplify (2 3 ) 2 This means 2 3 *2 3 2 3 *2 3 = (2*2*2)*(2*2*2)=2 6

3. Simplify (4 2 ) 3 This means 4 2 *4 2 *4 2 4 2 *4 2 *4 2 = (4*4)*(4*4)*(4*4)=4 6

4. How does this work? Look again (4 2 ) 3 = 4 6 (2 3 ) 2 =2 6 How do the exponents 2 and 3 relate to the exponent 6?

5. Let’s look at some more (3 3)4 = (3*3*3)*(3*3*3)*(3*3*3)*(3*3*3) (3 3)4 =3 ?? 3 (3x4) = 3 12 As you can see (3 3)4 shows 3 multiplied by itself 12 times. (3 3)4 = 3 (3*4) =3 12

6. Let’s try some using the Power of Powers Property The Power of Powers Property states that when you have a number to a certain power raised to another power, you multiply the exponents. Examples (3 3 ) 4 = 3 12 (8 2 ) 5 = 8 10 (9 1 ) 4 = 9 4

7. Try some (2 3)4 = ? (10 3)2 = ? (p 2)5 = ? (x m)3 = ? Go to the next slide when you have the solutions to check your work.

8. Power of Powers (2 3)4 = 2 12 (10 3)2 = 10 6 (p 2)5 = p 10 (x m)3 = x 3m

9. Raise a monomial to a power (xy) 2 = xy*xy = x*x*y*y = x 2 y 2 (xy 2 ) 2= If you get stuck with powers of powers, try writing out the multiplication of numbers and variables. (x*y*y)* (x*y*y) = x*y*y*x*y*y = x*x*y*y*y*y = x 2 y 4

10. Try some (xy) 2 = ? (xy 2 ) 2 = ? (  r 2 ) 4 = ? Go to the next slide when you have the solutions to check your work.

11. Solutions (x 1 y) 2 = x 2 y 2 (x 1 y 2 ) 2 = x 2 y 4 (  1 r 2 ) 4 =  4 r 8 Can you see the power of powers property at work? If not, try changing the variables that have no exponent to an exponent of one. {Once again, 1 comes in handy!}

12. Let’s take another look (xy) 2 =(x 1 y 1 ) 2 = x 2 y 2 (x 1 y 2 ) 2 = x 2 y 4 (  1 r 2 ) 4 =  4 r 8

13. Try some more. Use 1 to your advantage when you can. (x 2 y) 3 = (x 2 y 1 ) 3 = x (2*3) y( 1*3) = x 6 y 3 (x 2 y 2 z 2 ) 3 = (abcd) n = (x 2 y 3 ) 5 =

14. Solutions (x 2 y 2 z 2 ) 3 =x 2*3 y 2*3 z 2*3 =x 6 y 6 z 6 (abcd) n =a n b n c n d n (x 2 y 3 ) 5 =x 2*5 y 3*5 = x 10 y 15

15. Powers of -1 Write out (-2) 3 = (-2)*(-2)*(-2) When the exponent is an odd number, the answer can be negative.

16. Suggestion Once again, the suggestion is to write out the multiplication statements to help you solve tricky exponential products.

17. Simplify (-t) 5 =? (-t) 4 =? (-5x) 3 =?

18. solutions (-t) 5 = (-t) * (-t) * (-t) * (-t) * (-t) =-t 5 (-t) 4 =t 4 (-5x) 3 =(-5x) (-5x) (-5x) = = -5*-5*-5*x*x*x = -125x 3

19. Negative and Zero Exponents Integrated II Chapter 9.2

20. Negative Integers do NOT mean negative numbers

21. Numbers to the Zero Power Every number to the Zero Power, such as 5 0 = 1. We can use last lesson’s division of powers as a proof.

22. Using division to prove Any number divided by itself equals 1. Using the Quotient of Powers Property, the exponents would be subtracted. 6 5-5 = 6 0 = 1

23. Negative Exponents Negative Exponents do not mean negative numbers. 4 -5 = 3 -2 = 7 -4 =

24. Solve.

25. Simplify. b 6 *b -2 =b 4 = 1 b 4 b 4 -3y -2 -6p -7 8a 4 b 7 c -4 3a 6 b -6 c -4

26. Simplify. - 3y -2 = -3 y 2 -6p -7 = -6 p 7 8a 4 b 7 c -4 = 8 a 4-6 b 7--6 c -4--4 = 8 b 13 3a 6 b -6 c -4 3 3 a 2 ** (c 0 =1 which when multiplied is no longer part of the answer.

28. Let’s Divide! Dividing Monomials Focus: Quotient of Powers Rule

29. Quotients of Powers How do I find ? a*a*a*a*a*a = a*a*a*a a 2 1 = a 2 a*a*a*a*a*a = a*a*a*a

30. Let’s find a different way In the previous slide, you saw that the result of this fraction was a 2 . How do 6 and 4 relate to two?

31. Quotient of Powers Property For all non-zero numbers, subtract the exponent of the denominator from the numerator when the bases are the same. 4 5-2 = 4 3

32. Let’s prove it. 4 5-2 = 4 3

33. Try Some.

34. Solutions 2 10-5 = 2 5 3 10-7 = 3 3 5 8-3 = 5 5 2 3-2 = 2 1= 2

35. Try Some with variables. x j-1 x a+b-c x m+1-1 = x m

36. Fun Fun Fun

37. Fun Fun Fun -2x 2-1 y 5-3 =-2xy 2 -40a 4-1 b2c -5 = -40a 3 b 2 c 5

38. Remember negative exponents? Any time you have a negative exponent, it must be placed in the denominator. C -3 =

39. Try Some

40. answers

41. Combine two concepts

42. Combine two concepts (answers)

44. Thanks for enjoying math! Nothing will be due for today’s work.